传统飞行器的飞行速度、攻角、侧滑角、自由来流静压等大气数据参数通常利用探出飞行器的传感装置得到.利用Pitot管得到来流总压以确定来流速度, 利用探出飞行器表面的风标传感器得到攻角等.但高性能高速飞行器的发展需求, 对传统的飞行参数测量系统提出了极大的挑战[1].例如对某些高超声速飞行器而言, 严酷的气动加热使得探出的传感装置不可用; 现代某些高性能飞行器对隐身性能的需求使得传统的探出式测量系统应用受限,难以发挥其有效性能.
针对上述问题, NASA发展了嵌入式大气数据传感(flush air data sensing, FADS)系统. FADS系统的原理是基于特定区域的表面压力反推飞行参数, 其原理的可行性已通过各类飞机及航天飞行器进行了广泛的研究验证. NASA研究报告表明机载FADS系统已成功用于航天飞机[2-3]及X-33空天飞行器[4]的返回过程中.在有人控制飞行器F-14[5]及KC-135[6]的飞行测试中也验证了FADS技术的可靠性, 测试结果证实了FADS技术在各类飞行器应用的可行性.随后, 基于神经网络技术的FADS系统成功实现. Crowther等[7]通过风洞实验测试了位于战斗机机身的FADS系统测压孔配置方案; Calia等[8]利用神经网络算法计算了M-346喷气训练机的静压及Mach数, 通过风洞实验数据及飞行实验数据来训练及测试神经网络; Rohloff等[9-10]基于神经网络技术建立了位于F-18头部的FADS系统的风速计算方法. Samy等[11]将基于神经网络算法的FADS系统用于小型无人飞行器中, 建立了不同速度下的飞行参数误差分布.研究表明, FADS系统之所以选用神经网络算法, 是因为神经网络算法能够处理大批量的风洞实验及飞行实验数据而无须建立头部的气动模型.
国外研究表明, FADS系统已成功产业化并应用于多种钝前体飞行器[12-13].但针对尖楔外形飞行器, 由于尖楔前体各异, 并未发展出一套通用的FADS系统求解算法[14-16].鉴于该类型飞行器目前大多正处于实验阶段, 外形各异, 针对该型飞行器建立一套通用性较好的FADS系统的模型及解算方法,困难极大[17].因此, 对于FADS系统的求解算法, 并不是非常成熟与完善.前期的研究表明, 针对FADS系统建立的神经网络算法已成功用于配备有昂贵装备的大型、快速飞行器中, 且系统的精度较高, 但针对神经网络方法用于具有尖楔前缘飞行器FADS系统的分析, 研究工作较少, 且采用的网络训练样本数据点数太少, 无法充分反映神经网络算法在尖楔前体飞行器中应用的可靠性.
作为一种非线性建模预测手段, 神经网络技术在自适应性、模糊推理能力及自学习能力方面优势显著, 非常适用于解决非线性问题, BP神经网络及RBF神经网络是目前较为成熟和应用较为广泛的网络模型.针对本文研究的尖楔前体飞行器FADS系统气动建模困难的问题, 建立了基于RBF神经网络模型, 以代替FADS系统空气动力学模型, 使得FADS系统的解算不再依赖传统的空气动力学模型(这里的输入量还要依靠气动模型来确定, 解算方法完全替代气动模型的算法), 免去了相关校准参数的标定[18].同时鉴于神经网络本身的容错功能, 各层中个别单元出现错误也不会出现灾难性的后果[19].因此, 建立FADS系统的神经网络算法是一种较好的选择.基于此, 针对尖楔前体飞行器FADS系统的特点[20-21], 本文首先对测压孔的配置进行了探讨; 并基于RBF的神经网络技术建立了其结算模型及算法, 分析了算法的测试误差, 建立了气动延时效应及位置误差效应对求解精度的影响, 并对该模型的预测值与真实值进行了比较, 以期为人工神经网络技术在尖楔前体飞行器FADS系统中的进一步发展提供参考.
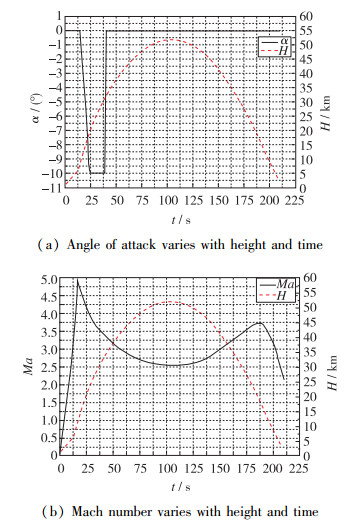
1 飞行器概述尖楔前体的头部外形如图 1所示.其长度约为2 400 mm, 上表面的半楔角为15°, 下表面为平板.飞行包线如图 2所示.本文研究的实验窗口如下:上升段, Ma=3.0~5.0, H=6.0~11.0 km; 下降段, Ma=3.5, H=30.0~9.0 km.

|
| 图 1 飞行器头部外形 Fig.1 Vehicle configuration |
|
| 图 2 飞行包线 Fig.2 Flight envelope |
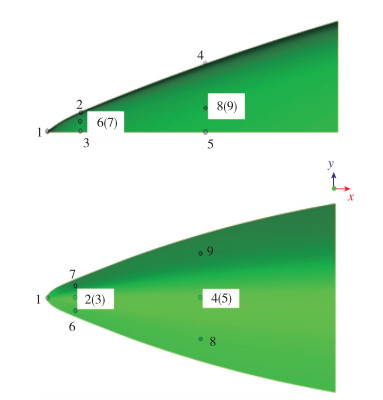
FADS系统是通过飞行器表面的测压孔测量表面来流压力, 根据建立的气动模型反推得到飞行参数, 测压孔配置对于FADS系统的精度至关重要, 尤其是对于本文建立的无物理模型的RBF神经网络模型.该方法略去了气动建模的过程, 但测压孔应尽量配置在与相应的飞行参数敏感的位置.针对该尖楔外形飞行器的特点及实际需求, 结合相关的空气动力学理论, 该FADS系统配置了9个测压孔, 位于攻角平面的5个测压孔及沿纵向中心线分布于上表面的4个测压孔, 用于Mach数、攻角、侧滑角及静压的建模及解算. FADS系统的测压孔具体配置方案如图 3所示.其中, 尖楔前缘驻点配置1个测压孔p1, 沿飞行器纵向对称面中心线上, 上、下表面各配置2个测压孔, p2, p4位于上表面, p3, p5位于下表面, 用于估计攻角、Mach数及静压. p6, p7, p8, p9位于机身上表面中心线两侧, 用于估计侧滑角.各个测压孔的位置信息为, 驻点测压孔1 :(0, 0, -0.002), 上表面测压孔2 :(18, 0, 9.611), 下表面测压孔3 :(18, 0, -0.002), 上表面测压孔4 :(126.770, 0, 41.591 2), 下表面测压孔5 :(126.770, 0, 0)(单位:mm).测压孔6, 7, 8, 9位于上表面, 其中, 测压孔6和7, 8和9分别与测压孔2和3, 4和5位于同一纵向截面, 沿侧向的坐标分别为y=±35 mm, y=±60 mm.
|
| 图 3 测压孔配置 Fig.3 Pressure ports configuration |
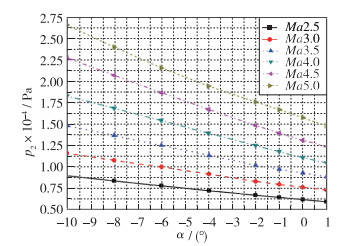
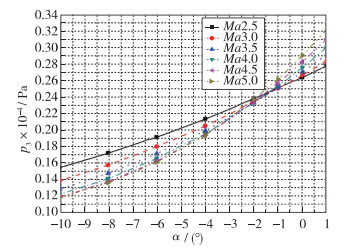
作为配置在攻角平面的测压孔, 用于Mach数、攻角及静压的建模及解算, 测压孔对Mach数、攻角及静压变化比较敏感, 才能充分反映相应飞行参数的变化信息, 从而建立起压力变化与对应参数之间的联系.以高度25 km为例, 对于测压孔的选取标准进行定量的分析及比较.测压点p2,p3压力在不同的Mach数下随攻角的敏感性分析如图 4~5所示.可以看出, 本文选取的测压孔的压力随Mach数及攻角变化显著.
|
| 图 4 p2随攻角及Mach数的变化趋势 Fig.4 Pressure p3 varies with Ma and angle of attack |
|
| 图 5 p3随攻角及Mach数的变化趋势 Fig.5 Pressure p3 varies with Ma and angle of attack |
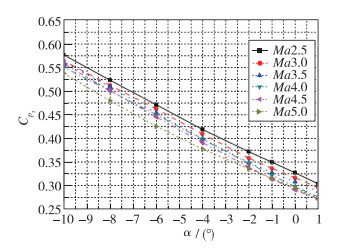
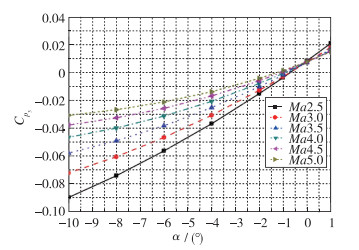
为了从理论上分析其规律性, 对压力系数进行了分析, 如图 6~7所示.本文压力系数定义为Cpi=(pi-p∞)/q∞, 其中Cpi为第i个测压孔的压力系数, pi为测压孔压力, p∞为来流静压, q∞为来流动压.可以看出, 压力系数的变化规律完全一致, 因此, 对于本文选取的测压孔配置, 理论上完全可行.同时, 对于测压孔压力系数分析的另一个目的是神经网络建模需要大批量的训练数据, 可以根据某一特定高度计算得到的压力系数转化成飞行包线范围内所需的各个高度上的压力数值, 从而极大减小计算量.
|
| 图 6 p2压力系数随攻角及Mach数的变化趋势 Fig.6 Pressure coefficient Cp2 varies with Ma and angle of attack |
|
| 图 7 p3压力系数随攻角及Mach数的变化趋势 Fig.7 Pressure coefficient Cp3 varies with Ma and angle of attack |
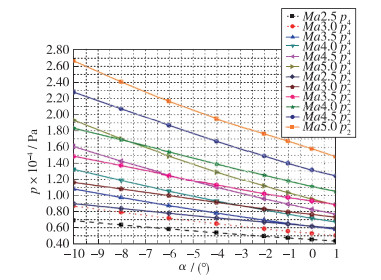
对于测压孔数值上的分析, 如图 8所示, p2与p4的数值上相差约30%, 完全可以与位置误差区分开, 反映不同测压孔位置的信息.因此, 本文选取的测压孔可以用于建立与攻角、Mach数及静压间的关系.
|
| 图 8 p2与p4数据对比 Fig.8 Pressure distributions for p2 and p4 |
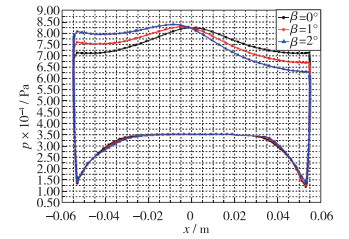
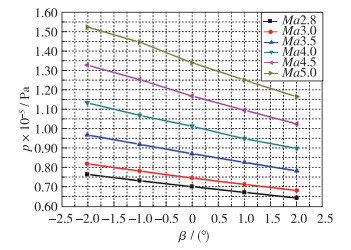
下面分析侧滑角的选取标准.首先, 配置的测压孔应位于对侧滑角敏感的区域, 以x=18 mm截面为例, 由于侧缘很尖, 配置测压孔困难, 所以, 测压孔应配置在中轴线与侧缘之间, 且对侧滑角的变化敏感.基于图 9的分析, 本文选取y=±35 mm位置的测压孔用于估计侧滑角.可以看出, 该区域是数值对于侧滑角最敏感的区域.基于图 10的p6随侧滑角及Mach数的变化趋势也可以说明, 本文选取的用于预测侧滑角的测压孔非常合适.
|
| 图 9 x=18 mm截面压力数值随侧滑角的变化趋势 Fig.9 Pressure distribution at x=18 mm section varies with angle of sideslip |
|
| 图 10 p6随侧滑角及Mach数的变化趋势 Fig.10 Pressure distributions for p6 varies with angle of sideslip and Mach number |
RBF网络算法以径向基函数作为隐含层单元的“基”, 构成隐含层空间, 并对输入矢量进行转换, 将低维模式输入量转换到高维空间内, 使得在低维空间内的线性不可分问题在高维空间内线性可分.本研究采用的径向基函数为Gauss函数. RBF神经网络是一种具有单个隐含层的3层前馈型局部逼近神经网络, 具有收敛速度快、逼近性能好、不存在局部极小等优点, 本文采用的是Li等[22]发展的RBF神经网络算法, 详细的算法流程将在下文中介绍.
3.2 RBF神经网络的算法设计典型的含有N个神经元的单隐含层单输出的RBF神经网络模型为
| $ {{\hat y}_k} = {\lambda _0} + \sum\limits_{i = 1}^N {{\lambda _{ki}}} {\varphi _i}(x)(k = 1, 2, \cdots , m) $ |
其中,
| $ \varphi_{i}(x)=\mathrm{e}^{\frac{-\left\|x-\mu_{i}\right\|^{2}}{\sigma_{i}^{2}}} $ |
其中, μi为隐含层第i个节点的Gauss函数的中心向量, 与输入量x的维数相同, σi为隐含层第i个节点的标准化常数, 它决定了基函数围绕中心点的宽度,
|
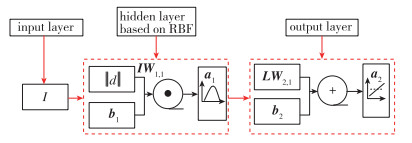
| 图 11 单隐含层的RBF神经网络模型 Fig.11 RBF neural network model with single hidden layer |
其中, I为输入层, IW1, 1为径向基层与输入层间的权值矩阵,
| $ {\mathit{\boldsymbol{a}}_1} = \phi \left( {\left\| {\mathit{\boldsymbol{I}}{\mathit{\boldsymbol{W}}_{1, 1}} \cdot \mathit{\boldsymbol{p}}} \right\|{\mathit{\boldsymbol{b}}_1}} \right) $ |
输出层为
| $ {\mathit{\boldsymbol{a}}_2} = f\left( {\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{W}}_{2, 1}}{\mathit{\boldsymbol{a}}_1} + {\mathit{\boldsymbol{b}}_2}} \right) $ |
其中, p为输入层I的输入向量矩阵, ϕ为径向基函数, f为线性函数.传统径向基函数的中心向量及标准化常数(Gauss函数的中心及宽度)固定, 训练算法仅用于训练RBF网络的连接权值.但固定了隐含层节点基函数的中心及宽度, 会使得网络结构增大, 训练时间增加, 而且确定合理的隐含层节点个数及对应的中心及宽度非常困难[22].本文建立的具体算法流程为:
(1) 将样本数据分为H类, 随机选取初始聚类中心μh(0), 1≤h≤H.
(2) 计算第r步所有的样本输入与聚类中心的距离
| $ \mathit{l}{\rm{(}}\mathit{r}{\rm{) = }}\left\| {\mathit{x}{\rm{(}}\mathit{r}{\rm{) - }}{\mu _\mathit{h}}\left( {r - 1} \right)} \right\| $ |
对于单输出的神经网络而言, 设定初始隐含层节点个数为零, 当(1)~(3)条件同时满足时增加隐含层的节点个数.
| $ {{s_r} = {y_r} - {{\tilde y}_r} > {\kappa _1}} $ | (1) |
| $ {q = \sqrt {\sum\limits_{i = r - (n - 1)}^r {\frac{{s_i^2}}{n}} } > {\kappa _2}} $ | (2) |
| $ {w = \left\| {x - \mu } \right\| > {\kappa _3}} $ | (3) |
其中, sr为输出目标值yr与估计值
| $ \boldsymbol{\kappa}_{3}=\max \left\{\delta_{\max }, \gamma, \delta_{\min }\right\} $ |
其中, γ为衰减常数, 0<γ<1, δmin为κ3的初始值, δmax为κ3的最终值. κ1, κ2是保证样本数据训练精度的参数, κ3检验当前隐含层节点与输入向量的距离足够小, 以保证至少一个隐含层节点对输入量敏感.当训练条件不全部满足(1)~(3)时, 算法仅对最活跃的神经元进行训练, 加速迭代; 该结构可自动移除训练过程中对网络结构影响最弱的神经元, 使得网络结构简单化.
(3) 将训练数据按近邻规则分组, 满足
| $ i\left(x_{j}\right)=\min \left\|x_{j}-\mu_{h}(r)\right\| $ |
时, xj归为第i类.
(4) 更新聚类中心
| $ {{\mu _i}(r + 1) = \frac{1}{{{n_i}}}\sum\limits_{x \in {\theta _i}(r)} x , i = 1, 2, \cdots , h} $ |
其中, ni为第i个聚类域中的样本数.
(5) 若μi(r+1)≠μi(r), 返回(2).
(6) 确定了隐含层参数及各节点的径向基函数的中心后, 采用递推最小二乘算法用于训练所建立的神经网络, 建立网络权值的调整算法, 从而得到输出层的权值矩阵
| $ {\theta _{r + 1}} = {\theta _r} - {\left. {\eta \frac{{\partial E}}{{\partial \theta }}} \right|_r} $ | (4) |
其中, θ为训练参数向量(将权值看做一组向量), η为学习率. E为均方差函数, 定义为
| $ E = \frac{1}{2}\sum\limits_{j = 1}^k {{{\left( {{y_j} - {{\mathit{\tilde y}}_j}} \right)}^2}} $ |
实际每次迭代中, 训练参数按方程(4)中所述的沿梯度相反的方向调整, 使得均方差最小, 直至收敛.在优化的目标函数中添加权值和阈值的调整项, 可以改善神经网络训练过程中的过拟合问题.只需要得到输入压力后, 将这些值作为输入量输入到神经网络中, 通过上述公式计算得到所需的输出.值得注意的是, 本文训练过程中将输入和输出都进行了归一化处理, 具体见下述章节, 因此使用时也须对相关数据进行相应的处理.
3.3 数据集生成将原始数据集分成训练数据集和测试数据集, 从原始数据中抽取一小部分作为测试数据, 其余作为训练数据.其中, 训练数据集用于训练神经网络中的权值和阀值, 监控计算过程中的训练误差; 测试数据集用于测试最后得到的神经网络的泛化能力, 得到泛化误差.根据第1节中飞行器的飞行包线, 在Mach数、静压及攻角范围内选择共计约2 000个数据点进行计算, 其中Ma=3.0, 3.5, 4.0, 4.5, 5.0;攻角-10°, -8°, -5°, -3°, -2°, -1°, 0°, 1°; 侧滑角-2°, -1°, 0°, 1°, 2°; 静压范围40 000~1 000 Pa, 获得足够多的样本点.其中, 1 800个数据点用于神经网络的训练, 另外的约200个数据点用于对训练好的网络进行测试.须说明的是, 训练数据集一定要覆盖所有的飞行包线数据, 以保证算法的预测精度.
3.4 网络输入及输出由于训练数据的范围宽广, 输入压力的变化范围很大, 为了更好地反映输入压力数据与输出参数之间的对应关系, 使得神经网络的训练有效, 本文采用数据归一化的方法对输入及输出的数据进行了处理, 具体为:
(1) 在训练数据的包线范围内找出各个输入的压力数据对应的最大值及最小值;
(2) 将输入的压力数据按照下式进行归一化处理
| $ {p_{i - {\rm{input}}}} = 2 \times \frac{{{p_i} - {p_{i\min }}}}{{{p_{i\max }} - {p_{i\min }}}} - 1 $ |
其中, pi-input为实际归一化后输入的第i个压力数据, pi为输入的第i个测压孔的实际压力, pimin为训练数据包络范围内第i个测压孔的压力最小值, pimax为训练数据包络范围内第i个测压孔的压力最大值.
(3) 网络的输出是归一化后的输出, 实际应用须进行反归一化, 即为
| $ \mathit{N}{\mathit{N}_{i - {\rm{output}}}} = 2 \times \frac{{{X_{i - {\rm{factual}}}} - {{\rm{x}}_{i\min }}}}{{{x_{i\max }} - {x_{i\min }}}} - 1 $ |
其中, NNi-output为名义输出的第i个飞行参数, Xi-factual为实际反归一化后输出的第i个飞行参数, ximin为输出的第i个飞行参数的最小值, ximax为输出的第i个飞行参数的最大值.
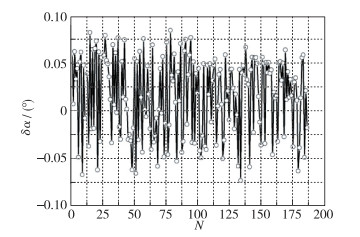
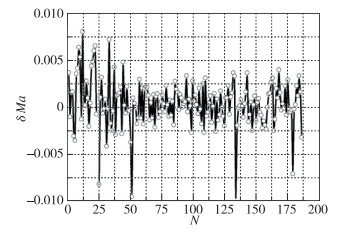
4 算法精度分析 4.1 测试精度分析利用3.2节建立的基于RBF的神经网络模型, 将压力数据1, 2, 3, 4, 5作为输入参数, 经过一系列的训练, 建立了攻角、Mach数及来流静压的神经网络, 针对每一个参数分别建立单输出的网络结构.基于建立的攻角、Mach数、侧滑角及来流静压的神经网络, 针对各个飞行参数的网络结构得到的攻角、Mach数、侧滑角及来流静压的误差分布如图 12~15所示.本节的测试精度并未考虑误差源模型的影响.可以看出, 基于RBF的人工神经网络算法解算精度较好, 攻角、Mach数及静压的测试误差输出(绝对值)分别小于0.1°, 0.01及150 Pa.因此, 从测试的飞行参数的总体测试误差分布来看, 基于神经网络算法的FADS系统解算精度较好.
|
| 图 12 攻角的测试误差分布 Fig.12 Test error distributions for angle of attack |
|
| 图 13 Mach数的测试误差分布 Fig.13 Test error distributions for Ma |

|
| 图 14 静压的测试误差分布(绝对误差) Fig.14 Test error distributions for static pressure |
|
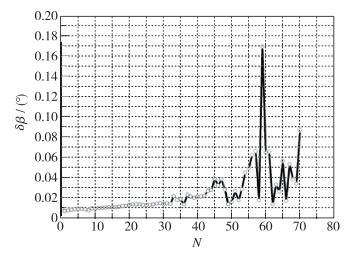
| 图 15 侧滑角的测试误差分布(绝对误差) Fig.15 Test error distributions for angle of side slip |
FADS系统用于实际飞行预测之前, 必须进行误差源模型的验证.实际FADS系统通过表面压力反推飞行参数, 任何对于压力测量有影响的因素都应该量化, 主要的误差源包括气动延迟效应、热荷载效应、传感器安装误差效应及传感器精度误差效应等[14], 如何准确地建立这些误差源对FADS系统精度的影响, 是一个比较困难但是必须要考虑的问题.随着实验条件的进步及计算条件的提高, 基于本文研究的飞行器的实际飞行包线及试飞需求, 本文主要针对对于FADS系统预测精度影响较大的两类误差源模型进行验证, 即气动延时及位置测量误差.
本文研究的FADS系统所用传感器空腔容积为153 mm3, 测压管最长长度为150 mm, 外径为2 mm, 内径为1 mm.达到稳定状态所需的时间T(延迟时间)满足
| $ T = \frac{{128\mu L\left( {V + 0.5LA} \right)}}{{{\rm{ \mathit{ π} }}{\mathit{D}^4}{c^2}{\rho _0}}} $ |
其中, c为当地声速, ρ0为气流密度, A=πD2/4为测压管的横截面积, D为测压管直径, L为测压管长度, V为测压管的体积, μ为动力黏性系数, 随着高度增加, 延迟效应越显著.典型延迟时间与高度的变化关系如表 1所示.
| 下载CSV 表 1 延迟时间与高度的变化关系 Tab.1 Relationship between the delay time and height |
实际处理流程为:采样时间与延迟时间的比较, 只要采样时间大于延迟时间, 延迟可以忽略不计.压力延迟误差的计算:沿弹道, 采用CFD计算数据, 然后进行拟合加密, 除以时间间隔, 再计算典型的弹道点延迟误差即可.利用最小二乘拟合程序进行拟合, 采用加密拟合点的方法确定时间间隔.
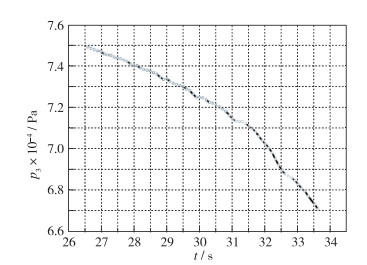
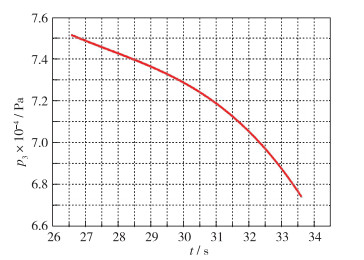
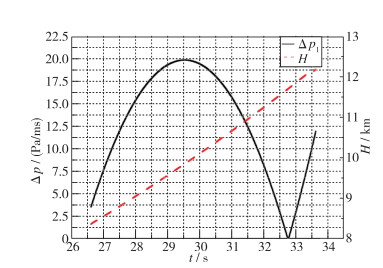
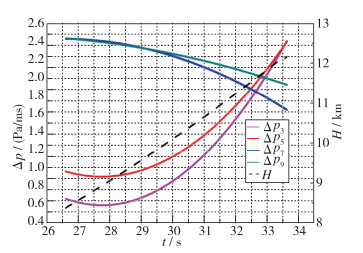
下面分析测压管路延迟对典型弹道产生的延迟压力差影响.应用CFD计算结果, 先对测压孔沿弹道的压力值进行拟合和弹道点加密, 将弹道点原来的0.1 s间距, 加密到0.01 s间距, 如图 16和17所示.对加密后的弹道点计算T-1和T时刻压差并除以0.01 s得到单位时间压力差, 测压孔p1, p3, p5, p7和p9的压力差随弹道时间的变化如图 18和19所示.
|
| 图 16 p3随弹道的变化(0.1 s间距) Fig.16 Pressure port p3 varies with flight envelope for time interval 0.1 s |
|
| 图 17 p3随弹道的变化(0.01 s间距) Fig.17 Pressure port p3 varies with flight envelope for time interval 0.01 s |
|
| 图 18 p1压差随弹道变化 Fig.18 Relationship between the pressure difference and time for p1 |
|
| 图 19 p3, p5, p7, p9压差随弹道变化 Fig.19 Relationship between the pressure difference and time for p3, p5, p7, p9 |
根据表 1中的时间延迟结果与图 18及图 19的各个测压孔压差随时间的变化曲线, 选取典型弹道点, 可以计算得出沿弹道时顶点p1最大延迟压力差小于30 Pa, p3, p5, p7和p9的最大延迟压力差小于5.0 Pa.根据随机测量误差影响计算得出, 顶点最大允许误差为800 Pa, 其他点最大允许误差为250 Pa, 测量管路延迟造成的压力误差对解算结果影响可以忽略.
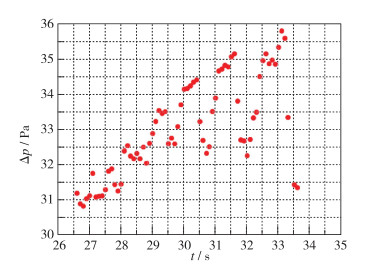
根据弹道点范围, 选取Ma=3.5, 5.0, 攻角-10°, 0°和2°状态, 这些状态基本上覆盖整个弹道范围, 计算轴向位置误差对压力的影响,如图 20所示.根据数值计算结果得出1 mm轴向位置偏差, 造成压力偏差约在0.1%以内.按照上面位置误差影响计算结果, 得出测压精度对位置误差的要求.由此得出0.1%和0.05%测压精度对轴向位置的最大偏差分别为1 mm和0.5 mm.综合来看, ±0.1 mm位置偏差就可以满足0.05%压力测量精度.测压孔的配置误差只要不大于0.1 mm, 由于位置偏差导致的测压孔压力误差对算法的预测精度影响就可控.
|
| 图 20 测压孔位置误差 Fig.20 Errors from the initial port misalignment for ±0.1mm |
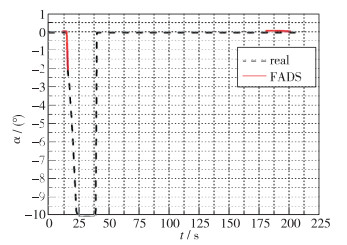
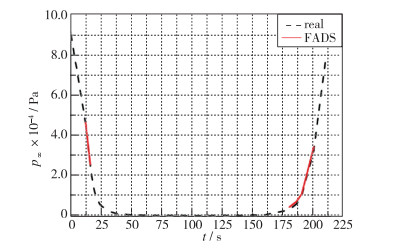
根据实际飞行器的飞行包线采集数据, 在上升段及下降段的任务窗口采集测压孔的数据信息, 输入到预测算法中进行验证, 得到的Mach数、攻角及静压的预测值与真实值的对比曲线如图 21~23所示.可以看出, 在实验任务窗口期, 通过FADS系统得到的攻角、Mach数及静压数值与真实值吻合较好, 充分说明了基于RBF神经网络建模技术建立的FADS系统的有效性.

|
| 图 21 基于神经网络建模的FADS系统的Mach数输出值与真实值的对比 Fig.21 Comparison of the RBF neural network estimation for Ma with the real value |
|
| 图 22 基于神经网络建模的FADS系统的攻角输出值与真实值的对比 Fig.22 Comparison of the RBF neural network estimation for angle of attack with the real value |
|
| 图 23 基于神经网络建模的FADS系统的静压输出值与真实值的对比 Fig.23 Comparison of the RBF neural network estimation for static pressure with the real value |
针对尖楔前体外形飞行器, 基于RBF神经网络建模技术建立了FADS系统的实现方案, 对其求解精度进行了分析, 得出的结论为:基于RBF神经网络技术建立的FADS系统模型, 测试精度较高; 全局误差分布较小, 完全可以满足FADS系统的精度需求.经沿飞行包线的实测数据与FADS系统输出数据比对, 高度吻合, 误差较小.结果表明, 针对尖楔外形测压孔配置特征, 基于RBF的人工神经网络算法解算精度较好, 考虑误差源模型的影响后, 攻角、侧滑角、Mach数及静压的网络输出预测值与真实值吻合较好, 输出的测试误差(绝对值)分别小于0.25°, 0.5°, 0.05及250 Pa.结果同时表明神经网络建模技术在尖楔前体飞行器用FADS系统中的有效性.
作为一种代替气动模型的建模方法, 神经网络算法在FADS系统中的应用前景广阔.由于实验状态所限, 数据点数并不多, 且并非全部的飞行包线都进行了测试.因此, 下一步将扩展飞行器的飞行包络, 对神经网络算法在尖楔外形FADS系统中的应用进行更为系统的论证.
| [1] |
Ellsworth J C, Whitmore S A. Simulation of a flush air-data system for transatmospheric vehicles[J]. Journal of Spacecraft and Rockets, 2008, 45(4): 716-732. DOI:10.2514/1.33541 |
| [2] |
Wolf H, Henry M W, Siemers Ⅲ P M. Shuttle entry air data system (SEADS)-flight verification of an advanced air data system concept[R]. AIAA 1988-2104, 1988.
|
| [3] |
Larson T, Siemers Ⅲ P M. Use of nose cap and fuselage pressure orifices for determination of air data for space shuttle orbiter below supersonic speeds[R]. NASA TR-1643, 1980.
|
| [4] |
Whitmore S A, Cobleigh B R, Haering E A. Design and calibration of the X-33 flush airdata sensing (FADS) system[R]. NASA/TM-98-206540, 1998.
|
| [5] |
Larson T J, Whitmore S A, Ehernberger L J, et al. Qualitative evaluation of a flush air data system at transonic speeds and high angles of attack[R]. NASA TR-2716, 1987.
|
| [6] |
Larson T J, Siemers Ⅲ P M. Subsonic Tests of an all-flush-pressure-orifice air data system[R]. NASA TR-1871, 1981.
|
| [7] |
Crowther W J, Lamont P J. A neural network approach to the calibration of a flush air data system[J]. The Aeronautical Journal, 2001, 105(1044): 85-95. DOI:10.1017/S0001924000011532 |
| [8] |
Calia A, Denti E, Galatolo R, et al. Air data computa-tion using neural networks[J]. Journal of Aircraft, 2008, 45(6): 2078-2083. DOI:10.2514/1.37334 |
| [9] |
Rohloff T J, Whitmore S A, Catton I. Air data sensing from surface pressure measurements using a neural network method[J]. AIAA Journal, 1998, 36(11): 2094-2101. DOI:10.2514/2.312 |
| [10] |
Rohloff T J, Whitmore S A, Catton I. Fault-tolerant neural network algorithm for flush air data sensing[J]. Journal of Aircraft, 1999, 36(3): 541-549. DOI:10.2514/2.2489 |
| [11] |
Samy I, Postlethwaite I, Gu D W, et al. Neural-network-based flush air data sensing system demonstrated on a mini air vehicle[J]. Journal of Aircraft, 2010, 47(1): 18-31. DOI:10.2514/1.44157 |
| [12] |
Cobleigh B R, Whitmore S A, Haering E A Jr, et al. Flush airdata sensing (FADS) system calibration procedures and results for blunt forebodes[R]. NASA/TP-1999-209012, 1999.
|
| [13] |
Whitmore S A, Mores T R, Larson T J. High angle-of-attack flush air data sensing system[J]. Journal of Aircraft, 1992, 29(5): 915-919. DOI:10.2514/3.46262 |
| [14] |
Whitmore S A, Moes T R. Measurement uncertainty and feasibility study of a flush airdata system for a hypersonic flight experiment[R]. NASA TM-4627, 1994.
|
| [15] |
Wang P, Jin X, Zhao X J. Application of the FADS system to hypersonic flight vehicles with sharp wedged fore-bodies[R]. AIAA 2012-5898, 2012.
|
| [16] |
王鹏, 金鑫, 张卫民. FADS系统在尖楔前体高超声速飞行器中的应用[J]. 中国科学:物理学力学天文学, 2013, 43(9): 1105-1110. Wang P, Jin X, Zhang W M. Application of FADS system in hypersonic flight vehicles with sharp wedged fore-bodies[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2013, 43(9): 1105-1110. (in Chinese) |
| [17] |
Ellsworth J C. An analytical explanation for the X-43A flush air data sensing system pressure mismatch between flight and theory[R]. AIAA 2010-4964, 2010.
|
| [18] |
王鹏, 金鑫, 张卫民, 等. 钝头机体用FADS系统的校准[J]. 实验流体力学, 2016, 30(2): 97-102. Wang P, Jin X, Zhang W M, et al. Calibration for the FADS system applied to the vehicle with blunt fore-bodies[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(2): 97-102. (in Chinese) |
| [19] |
张斌, 于盛林. 嵌入式飞行参数传感系统的神经网络算法[J]. 航空学报, 2006, 27(2): 294-298. Zhang B, Yu S L. Neural network algorithm for flush airdata sensing system[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(2): 294-298. DOI:10.3321/j.issn:1000-6893.2006.02.026 (in Chinese) |
| [20] |
王鹏, 李秋红, 胡远思, 等. 尖楔前体飞行器FADS-α的求解精度研究[J]. 中国科学:物理学力学天文学, 2015, 45(12): 124709. Wang P, Li Q H, Hu Y S, et al. Research on solving accuracy for FADS-α applied to the vehicle with sharp wedged fore-bodies[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(12): 124709. (in Chinese) |
| [21] |
王鹏, 胡远思, 金鑫. 尖楔前体飞行器FADS系统驻点压力对神经网络算法精度的影响[J]. 宇航学报, 2016, 37(9): 1072-1079. Wang P, Hu Y S, Jin X. Effect of stagnation pressure on the neural network algorithm accuracy for FADS system applied to the vehicle with sharp wedged fore-bodies[J]. Journal of Astronautics, 2016, 37(9): 1072-1079. DOI:10.3873/j.issn.1000-1328.2016.09.006 (in Chinese) |
| [22] |
Li Y, Sundararajan N, Saratchandran P. Analysis of minimal radial basis function network algorithm for real-time identification of nonlinear dynamic systems[J]. IEE Proceedings -Control Theory and Applications, 2000, 147(4): 476-484. DOI:10.1049/ip-cta:20000549 |
| [23] |
王鹏, 胡远思, 金鑫. 尖楔前体飞行器FADS系统的神经网络算法[J]. 空气动力学学报, 2017, 35(6): 777-780. Wang P, Hu Y S, Jin X. Neural network algorithm for FADS system applied to the vehicles with sharp wedged fore-bodies[J]. Acta Aerodynamica Sinica, 2017, 35(6): 777-780. DOI:10.7638/kqdlxxb-2015.0064 (in Chinese) |



