绕过压缩拐角的复杂流动普遍存在于高超声速飞行器的局部流场中, 如进气道、襟翼等.有关研究历经了半个多世纪[1-6], 但是, 由于激波边界层干扰的复杂性, 仍有许多问题需要深入探讨.过去的大量研究多关注湍流流动, 而层流边界层抵御逆压梯度的能力相较于湍流更弱, 因而容易发生分离, 且分离范围更大.近年来临近空间高超声速飞行器长时间在空气较稀薄的高空巡航飞行, 当地Reynolds数较低, 通常为层流绕流, 因此, 对于层流流场中的激波边界层干扰的研究逐渐成为热点[7-10].此外, 以往的研究多注重二维特性, 对于有限展宽的三维效应关注较少.
在本世纪初, 李素循等[11-12]通过风洞实验研究了高超声速(Ma=8)绕过不同压缩角(10°, 20°, 30°, 40°)的层流激波边界层干扰问题, 给出了干扰区内横向3个不同位置处沿纵向的压力和热流分布, 不但分析了压缩角对于压力和热流分布的影响, 而且表明了明显的三维效应.尤其在压缩楔体的侧面平板上, 实验结果表明存在明显的低压区(当地静压小于平板上未干扰区的压力), 但是在这一区域的热流测量结果要高于平板上未干扰区的热流值, 即在侧缘某些区域内表面压力分布与热流分布规律是相反的, 它们之间无相似性, 也不可比拟.
本文采用文献[11]的三维压缩拐角实验模型, 进行了数值模拟, 压缩角度分别选择20°, 30°, 在纵向3条线上, 与实验测压结果进行了对比, 表明了三维楔的侧缘存在低压区, 数值模拟结果给出了较大的低压区范围.通过对流场数值结果的进一步分析, 表明最低压力值发生在比实验结果更加靠近楔体的位置, 一个从楔体侧缘尖端发起的二次涡从此处掠过, 其抽吸作用是造成当地低压的主要原因.这种绕过压缩拐角流动的侧面三维效应, 不论来流是层流还是湍流均未见前人述及.此外, 数值结果表明在三维楔后缘处压力有所降低, 是由于楔体底部的低压通过边界层的亚声速区上传对上游的压力产生了影响.
1 数值方法与计算模型 1.1 数值方法采用三维可压缩Navier-Stokes方程为控制方程, 通过有限体积方法进行离散, 对流项离散采用Roe格式[13], 通过MUSCL插值达到2阶精度, 黏性项离散采用中心差分格式, 时间项离散使用隐式LU-SGS方法[14], 进行稳态流场计算.
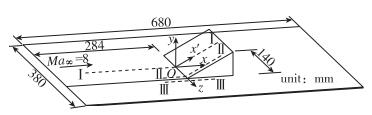
1.2 计算模型图 1为文献[11]采用的实验模型, 是由680 mm×380 mm的基础大平板和可改变角度的三角楔体两部分组成.在表面沿纵向布有3条测量线, 分别是Ⅰ线:沿模型的对称线布置; Ⅱ线:距模型对称线58 mm; Ⅲ线:距离模型对称线80 mm, 由于三维楔体的横向总宽度为140 mm, 所以Ⅲ线实际上位于楔体侧面平板上, 距离楔体侧面10 mm.
坐标原点位于模型对称线与楔体前缘交点, 以O标示, x轴与来流方向一致, y轴垂直于大平板表面.在3条测量线上沿楔面的压力分布结果按照x'坐标给出, x'自原点O沿楔面指向下游.
文献[11]说明实验是在中国航天空气动力技术研究院FD-20轻活塞式炮风洞内进行的, 选择了名义Mach数Ma = 8的喷管.
根据流场对称性, 本文的计算区域沿对称线取模型的一半, 采用分区对接方式进行网格划分.横向取140 mm(zmax=140 mm).上游自平板前缘始, 往下游延伸Lx, 对于楔角20°情况, Lx分别取441.87 mm和741.87 mm, 即分两种情况进行模拟, 一种情况计算到楔体的后端面; 另一种情况自楔体的后端面再向下游延伸300 mm.对楔角30°情况仅计算到楔体的后端面(Lx=429.49 mm).所以共有3个计算模型, 如表 1所示.
| 下载CSV 表 1 计算模型网格数 Tab.1 Grid number of each model |
按照实验条件, 计算参数为:自由来流Mach数Ma∞=8.0, 总压P0=6.0 MPa, 总温T0=1 100 K, 来流介质为空气, 单位Reynolds数Re=7.053×106/m, 以平板前缘至楔体前缘距离为特征长度定义的当地Reynolds数Re=2.03×106.实验已表明在三维楔体处仍然为层流流动, 因此按定常层流条件进行计算.
1.4 边界条件(1) 入流边界:来流为高超声速, 下游流场不影响上游流场, 在入流边界处给定来流的静压、静温及Mach数.
(2) 出流边界:出口为超声速下游流场不影响上游流场, 将所有参数数值外推.在大平板的侧缘同样采用出流边界条件.
(3) 物面边界:固壁采用无滑移条件.由于针对FD-20的实验条件, 有效实验时间只有几十毫秒, 因此采用等温壁面条件Tw=295 K.
(4) 对称边界:对称面上法向速度为零, 所有变量的法向梯度为零.
2 计算结果及分析 2.1 计算方法的检验图 2(a)为采用模型2(20°压缩角)的流场对称面计算等压力线, 图 2(b)为实验纹影照片[11].对比可见, 主要流场结构如前缘激波、主压缩斜激波、分离激波以及两者相交形成的三叉激波等结构, 计算和实验相符合.

|
| 图 2 流场结构计算与实验对比 Fig.2 Comparison of flow structures obtained by simulation and experimentation |
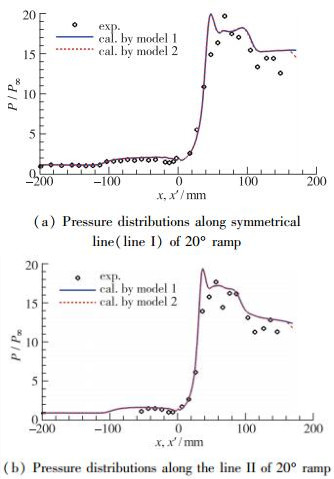
图 3(a)给出20°压缩角模型对称线(Ⅰ线)上的压力分布计算结果与实验值的比较.当地压力用自由来流静压P∞无量纲化, 图中给出P/P∞随x或x'(原点左边为x, 右边为x')的变化, 其中空心圆代表实验测量结果, 实线为模型1的计算结果, 虚线为模型2的计算结果.模型1的计算出口边界设在三维楔体的后端面处, 模型2计算范围往下游延伸了300 mm.但是, 在绝大部分区域内实线和虚线是重合的.楔面后缘点上, 模型2的压力值比模型1低了大约6%.这是因为, 模型2的计算区域包含了楔体后部的尾流区, 低压扰动会沿边界层近壁面的亚声速区向上游传播, 所以在楔面靠近后缘时压力减小, 但是其影响范围比较小, 压力分布线的分叉点到后缘点距离约为10 mm.
|
| 图 3 20°压缩拐角压力分布计算与实验对比 Fig.3 Comparison of pressure distributions obtained by simulation and experimentation(20° ramp) |
在Ⅰ线平板上(x < 0)的计算压力与实验结果符合较好, 在x=-106 mm位置, 即压力开始抬升处, 对应着分离区的边界, 图中表明数值预测的分离位置与实验结果十分接近.在楔面上(x'>0), 计算结果与实验有一些差别.特别是压力峰值位置, 计算点比实验点前移了大约15 mm, 压力峰值点对应着分离流动的再附位置, 这说明数值预测再附点还不能令人满意, 但是压力峰值大小与实验结果比较接近.此外, 数值计算采用了全流场层流模拟, 而风洞实验[11]仅说明在压缩角上游平板为层流边界层, 但是流动经过斜激波后, 在斜面的流动再附区内, 边界层是否发生转捩没有给出说明, 这也有可能是导致计算和实验结果差异的一种原因.
图 3(b)为20°压缩角Ⅱ线的压力分布对比, 由于平板上实验测压点较少, 难以判定实验反映的分离位置, 但是平板上计算和实验值的大小比较接近.在楔面上, 除了计算压力峰值略高于实验结果外, 压力分布对比情况和Ⅰ线的结果基本类似, 同样计算峰值比实验结果靠前, 而在后缘点, 模型2的压力计算结果要比模型1的低, 同样是由于楔体后部尾流区内的低压影响造成的, 因此在对类似的流场进行模拟时, 应该关注下游计算范围的选取.
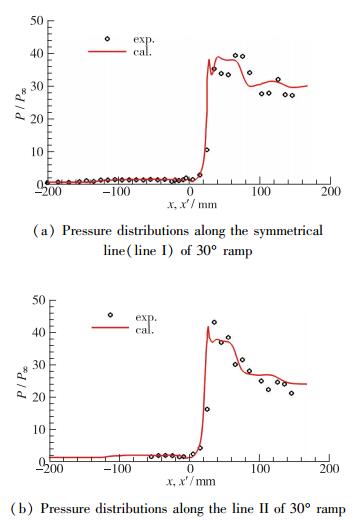
图 4(a), 4(b)分别给出了30°压缩拐角(模型3)在Ⅰ, Ⅱ线上的计算压力和实验结果的分布对比.在平板干扰区内, 计算和实验也符合较好, 数值计算的分离范围略小于实验结果.在楔面上, 计算压力与实验值的大小比较接近, 但是峰值位置有一定的差距.虽然30°压缩拐角模型网格量要远大于20°压缩拐角模型(见表 1), 但是计算精度没有得到提高.
|
| 图 4 30°压缩拐角压力分布计算与实验对比 Fig.4 Comparison of pressure distributions obtained by simulation and experimentation(30° ramp) |
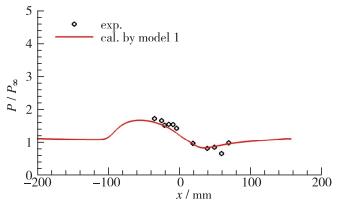
图 5给出20°压缩角沿Ⅲ线(z=80 mm)的计算压力与实验结果的对比.可以看出, 数值模拟除了没有捕捉到最低压力值外, 与实验测压结果比较接近, 在这条压力测量线上, 实验测得的最低压力(P/P∞)是0.66, 计算得到的是0.82, 但是不论计算还是实验, 都反映出在楔体的侧缘存在低于未干扰压力(即P/P∞ < 1)的区域.
|
| 图 5 20°压缩拐角表面Ⅲ线压力分布对比 Fig.5 Pressure distributions along the line Ⅲ of 20° ramp |
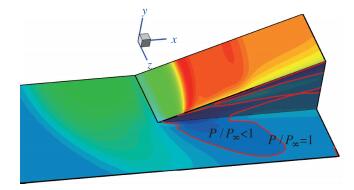
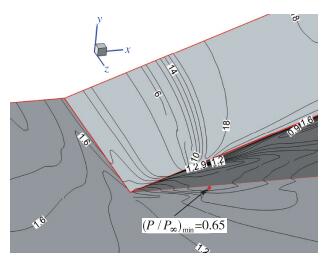
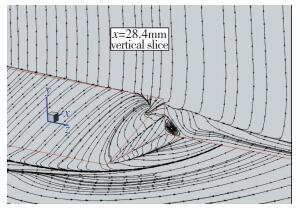
图 6给出计算表面压力云图(模型1), 图中通过P/P∞=1的线描绘出了一个较大的低压区范围, 图 7为楔体侧缘的等压力线局部放大图, 在x=28.4 mm, z=73 mm的位置, 计算给出最低的压力值为P/P∞=0.65, 而实验测量线Ⅲ位于z=80 mm, 计算得到的最低压力更靠近楔面且前移.实际上, 在文献[12]中还给出了热流测量结果, 其中沿Ⅲ线的热流密度在此处明显上升, 说明在这一区域内表面压力和热流分布规律是相反的, 通过本文的计算结果, 可以看出低压力范围比较大.因此, 在通过工程算法计算此处的热流时应引起注意.图 8为20°压缩拐角计算表面极限流线图谱, 同时给出了x=28.4 mm处横向截面上的流线图.从图中可以看出, 从三维楔的尖角处产生了一个二次涡, 开始时逐渐扩大, 扩展到最低压力位置处就基本保持不变, 涡核距侧缘的距离大约为3 mm(z=73 mm), 正好经过最低压力处, 所以二次旋涡的抽吸作用是低压产生的主要原因.
|
| 图 6 20°压缩拐角计算表面压力云图 Fig.6 Pressure cloud of 20° ramp by computing |
|
| 图 7 20°压缩拐角局部计算表面压力等值线 Fig.7 Local pressure contours of 20° ramp by computing |
|
| 图 8 20°压缩拐角低压区局部极限流线 Fig.8 Local streamlines at low pressure region of 20° ramp |
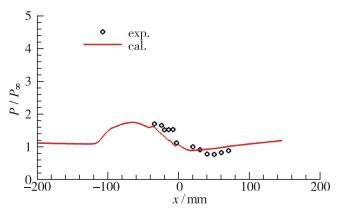
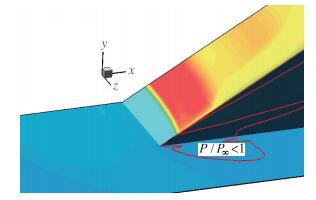
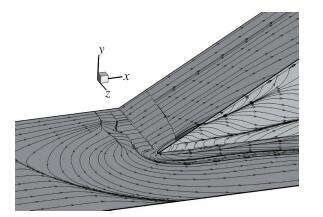
通过图 6的压力云图, 并结合图 3,图 4给出的Ⅰ, Ⅱ线之间的压力分布对比, 可以看出, 虽然Ⅱ线的位置比较靠近楔体的侧缘(距侧缘12 mm), 但是, 不论是实验结果, 还是计算结果, 在平板上和楔面上游的大部分区域内, 压力分布的差异不大, 可近似看做二维流动, 只是在楔面靠近侧缘的区域三维效应比较明显. 图 9为30°压缩角沿Ⅲ线(z=80 mm)的压力计算与实验结果的比较.同样在楔面上大部分区域呈二维特性.而在楔体侧面平板上存在P/P∞ < 1的区域, 但是在Ⅲ线这个特定位置上, 实验测得的低压值是P/P∞=0.77, 计算最低压力是P/P∞=0.88.而在图 10所示的全表面压力等值线图中反映的计算最低压力值为P/P∞=0.66, 位于x=11.8 mm, z=71.5 mm, 此处同样是由尖角处产生的二次涡的涡核所扫过的位置(见图 11).
|
| 图 9 30°压缩拐角表面Ⅲ线压力分布对比 Fig.9 Pressure distributions along the line Ⅲ of 30° ramp |
|
| 图 10 30°压缩拐角计算表面压力云图 Fig.10 Pressure cloud of 30° ramp by computing |
|
| 图 11 30°压缩拐角计算表面极限流线 Fig.11 Streamlines of 30° ramp by computing |
本文利用数值模拟方法研究了高速来流与绕过三维压缩拐角层流激波/边界层干扰流动, 并与实验结果进行了对比, 可见:
(1) 采用三维N-S方程, 2阶Roe格式及有限体积计算方法.得到的对称面流场结构与实验纹影照片符合较好, 在特定的纵向测量线上计算和实验的压力值进行了对比, 平板分离区内符合较好, 楔面上在再附线附近峰值位置有所偏差, 但是峰值大小基本一致.表明数值方法可以较好地模拟分离位置, 但对再附位置的模拟精度不足(风洞实验是否在再附区发生了转捩需要进一步探讨).
(2) 通过楔体侧面的压力分布数值模拟结果, 进一步细化了实验中发现的低压区, 但是计算最低压力并不在实验给出的Ⅲ线上, 而是更加靠近楔体侧面.此处的低压主要是由于自楔体尖角处发生的二次涡的抽吸作用造成的.数值模拟结果可以更为全面、细致地补充三维流场特性, 由于已有实验数据可以在特征位置上对比两种结果, 说明了计算方法的合理性和可信性.
(3) 不论是20°还是30°楔体的侧面平板上都存在较大的低压区, 在应用压力与热流相关的工程预测方法时应当引起注意.但是由于低压区位置楔体几何形状的特殊性, 严重影响本数值方法采用的结构网格对于热流模拟的精度, 因此没有获得合理的热流数值模拟结果以便与实验测热结果进行比对.
| [1] |
Lewis J E, Kubota T, Lees L. Experimental investigation of supersonic laminar, two-dimensional boundary layer separation in a compression corner with and without cooling[J]. AIAA Journal, 1968, 6(1): 7-14. DOI:10.2514/3.4434 |
| [2] |
Holden M S. Shock wave-turbulent boundary layer interaction in hypersonic flow[J]. Proceedings of the 15th Aerospace Sciences Meeting, Los Angeles, CA, USA: AIAA, 1977. http://www.researchgate.net/publication/268453601_Shock_wave-turbulent_boundary_layer_interaction_in_hypersonic_flow
|
| [3] |
Mallinson S G, Gai S L, Mudford N R. The interaction of a shock wave with a laminar boundary layer at a compression corner in high-enthalpy flows including real gas effects[J]. Journal of Fluid Mechanics, 1997, 342(1): 1-35. |
| [4] |
Li S X, Chen Y K. A study of interaction flow induced by 3D wedge[C]. Proceeding of the 3rd International Conference Fluid-Mechanics, Kaliningrand, Moscow Region, Russia, 1997.
|
| [5] |
Candler G V, Nompelis I, Holden M S. Computational analysis of hypersonic laminar viscous-inviscid interac-tions[C]. Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA: AIAA, 2000. http://www.researchgate.net/publication/269068220_Computational_analysis_of_hypersonic_laminar_viscous-inviscid_interactions?ev=auth_pub
|
| [6] |
Dolling D S. Fifty years of shock-wave/boundary-layer interaction research:what next?[J]. AIAA Journal, 2001, 39(8): 1517-1531. DOI:10.2514/2.1476 |
| [7] |
崔尔杰. 近空间飞行器研究发展现状及关键技术问题[J]. 力学进展, 2009, 39(6): 658-673. Cui E J. Research statutes, development trends and key technical problems of near space flying vehicles[J]. Advances in Mechanics, 2009, 39(6): 658-673. DOI:10.3321/j.issn:1000-0992.2009.06.007 (in Chinese) |
| [8] |
Holden M S. Historical review of experimental studies and prediction methods to describe laminar and turbulent shock wave/boundary layer interactions in hypersonic flows[C]. Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Mee-tings. Reno, Nevada: AIAA, 2006.
|
| [9] |
李艳丽, 李素循. 高超声速绕钝舵层流干扰流场特性研究[J]. 宇航学报, 2007, 28(6): 1472-1477. Li Y L, Li S X. Investigation of interactive hypersonic laminar flow over blunt fin[J]. Journal of Astronautics, 2007, 28(6): 1472-1477. DOI:10.3321/j.issn:1000-1328.2007.06.007 (in Chinese) |
| [10] |
Bathel B F, Prahladh S I, Mahesh K, et al. Comparing experiment and computation of hypersonic laminar boun-dary layers with isolated roughness[C]. Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, Maryland: AIAA, 2014. http://arc.aiaa.org/doi/abs/10.2514/6.2014-0236
|
| [11] |
李素循, 倪招勇. 高超声速层流干扰流场研究[J]. 宇航学报, 2003, 24(6): 547-551, 573. Li S X, Ni Z Y. Investigation of laminar interactive flowfield in hypersonic flow[J]. Journal of Astronautics, 2003, 24(6): 547-551, 573. DOI:10.3321/j.issn:1000-1328.2003.06.001 (in Chinese) |
| [12] |
李素循. 激波与边界层主导的复杂流动[M]. 北京: 科学出版社, 2007.
|
| [13] |
Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computa-tional Physics, 1981, 43(2): 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [14] |
Kandula M. Buning P G. Implementation of LU-SGS algorithm and roe upwinding scheme in overflow thin-layer navier-stokes code[C]. Proceedings of Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences, Colorado Springs, CO, USA: AIAA, 1994. http://www.researchgate.net/publication/269056415_Implementation_of_LU-SGS_algorithm_and_Roe_upwinding_scheme_in_OVERFLOW_thin-layer_Navier-Stokes_code
|