高超声速的概念, 是由著名空气动力学家钱学森创造性地提出的, 通常以自由来流Mach数大于5作为高超声速流动的判断标准.此外, 薄激波层、强黏性效应、高熵层、高温真实气体效应、低密度稀薄气体效应等也是高超声速流动的主要特征[1].
先进的气动布局设计是发展高超声速飞行器的关键技术之一, 而乘波体是一种典型的高超声速飞行器构型, 其最显著的特征是弓形激波附着于整个前缘, 会有很高的升阻比[2-3].此外, 乘波体外形是根据精确解的流场设计而成的, 可以实现参数化以寻找优化构型[4-5].虽然乘波体优点很多, 但仍然有许多不足之处.首先, 有效容积率偏低.其次, 尖锐的前缘会在机头处产生很大的气动热, 从而温度升高, 热载荷增大.更重要的是, 乘波体是在特定的条件下设计的, 在偏离设计条件下, 气动特性会出现一定的恶化[6].所以在工程实验中, 以乘波体为前体的高超声速飞行器大多使用火箭发射来避开低速时遇到的问题, 这样便无法实现单级入轨的目标了.
自提出乘波体的设计思想以来, 国内外都已开展了较为成熟的研究[7-10], 而如何提高乘波体的非设计状态气动性能一直以来是研究的热点和难点[11-13].近年来, 通过优化乘波体的几何生成方法改善其低速气动特性, 已成为一种有效的研究途径.其中, Rodi提出了涡升力乘波体的概念, 有效兼顾了乘波体的高低速气动特性[14-15].目前, 国内仅有王发民等[16]、李世斌等[17]、段焰辉等[18]以宽速域乘波体为目标, 对乘波体非设计状态进行气动特性研究, 而这些研究也只是刚刚起步, 亟待深入探索.
本文首先对锥导乘波体的设计方法进行了研究, 并基于CATIA二次开发技术实现了锥导乘波体的参数化设计.通过对乘波体设计参数的研究, 获得了大后掠角乘波体构型.然后, 采用北航阎超教授课题组自主研发的MI-CFD软件平台对流场进行求解[19], 获得了乘波体高速和低速时的气动特性曲线, 并进行了流场机理的分析.研究发现, 乘波体具有高速时优异的乘波特性, 低速时能够产生数量可观的涡升力, 满足宽速域飞行的设计目标.
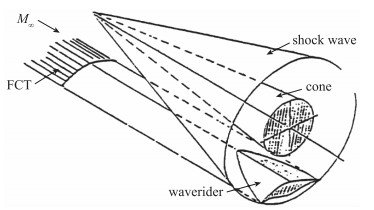
1 乘波体的参数化设计 1.1 锥导乘波体的生成方法由圆锥绕流生成的乘波体称作锥导乘波体, 其原理见图 1.首先选定设计Mach数及一个基准圆锥, 然后求该圆锥绕流的解.其次, 选定一个柱面作为流动捕获管(flow capture tube, FCT)与圆锥激波面相交, 形成乘波体前缘.再在前缘曲线上选取若干个点, 求得各点在激波后流场中的流线, 组成流面, 构成乘波体的下表面, 而上表面的确定则是通过形成自由流面实现的.这样组合起来, 就构成了乘波体的前体外形.不同的圆锥角、流动捕获曲线、流动捕获曲线与圆锥交线的轴向位置, 或者结合起来, 构成了不同的乘波体外形.
|
| 图 1 锥导乘波体示意图 Fig.1 Diagram of cone-derived waverider |
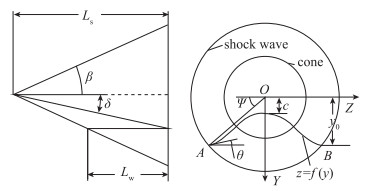
本文采用无黏锥导方法生成所需乘波体.根据上面的锥导乘波体生成原理, 确定来流Mach数, 半锥角δ, 无黏流场的长度Ls和乘波体上表面底部型线后, 即可唯一确定乘波体的外形[20-21].选取变化及适应性较好的四次曲线y=az4+bz2+c模拟上表面底部型线, 乘波体外形参数化如图 2所示.其中, 定义参数k=c/y0, Ψ为OA与水平轴(即Z轴)的夹角, θ为底部型线在A点的切线与水平方向的夹角, 确定k, Ψ, θ, 则上表面底部型线确定, 加上控制流场的Mach数和半锥角后, 控制乘波体外形生成的参数共有6个, 分别是M, Ls, δ, Ψ, θ和k.
|
| 图 2 锥导乘波体参数化示意图 Fig.2 Diagram of cone-derived waverider parameterization |
以后掠角为目标函数, 在乘波体设计的6个参数中进行灵敏度分析, 发现较为敏感的参数是δ和Ls.其中, δ对后掠角影响最大, 而且δ越大, 后掠角就越大, 构型越显得宽肥, 容积效率也越高; δ越小, 后掠角就越小, 构型更趋近于细长型, 容积效率越低.激波流场长度Ls控制乘波体机身长度Lw, 并影响构型截面与弓形激波的相对位置, 对低速条件下涡的生成也有很大的影响.所以在宽速域乘波体的设计中, 主要考虑这两个参数.
图 3为底部型线一致(即M, Ψ, θ和k相同), 而δ和Ls从左至右分别为10°和8 m, 18°和5 m, 30°和4 m时的情况, 可见其后掠角逐渐增大.

|
| 图 3 不同参数下的乘波体平面图 Fig.3 Waverider plane under different parameters |
乘波体的有效容积率定义为[22]:
| $ \mathit{\eta }{\rm{ = }}\frac{{{{\left( {{\rm{36 \mathit{ π} }}} \right)}^{{\rm{1/3}}}}{\mathit{V}^{{\rm{2/3}}}}}}{{{\mathit{S}_{\rm{w}}}}} $ |
其中Sw为浸润面积, 可以通过离散表面积分公式求得:
| $ {\mathit{S}_{\rm{w}}}{\rm{ = 2 \times }}\sum\limits_{\mathit{i}{\rm{ = 1}}}^\mathit{N} {{\rm{0}}{\rm{.5}}} \left[{\mathit{L}\left( \mathit{i} \right){\rm{ + }}\mathit{L}\left( {\mathit{i-}{\rm{1}}} \right)} \right]\sqrt {{{{\rm{(\Delta }}\mathit{y}{\rm{)}}}^{\rm{2}}}{\rm{ + (\Delta }}\mathit{z}{{\rm{)}}^{\rm{2}}}} $ |
L(i)为前缘第i个点沿自由来流方向的长度.
升阻比是乘波体一个很重要的性能参数, 也是区别于其他升力体的重要指标, 其计算公式:
| $ \frac{\mathit{L}}{\mathit{D}}{\rm{ = }}\frac{\mathit{L}}{{{\mathit{D}_{\rm{w}}}{\rm{ + }}{\mathit{D}_{\rm{f}}}{\rm{ + }}{\mathit{D}_{\rm{b}}}}} $ |
作用在乘波体的气动力可以在乘波体表面通过积分气动方程得到.在计算中, 为了消除底部阻力Db, 假定pb=p∞.虽然会存在误差, 但这在设计初期是可以接受的.则乘波体激波阻力计算为:
| $ {{\mathit{D}}_{\rm{w}}}\rm{=}\mathit{\boldsymbol{F}}\cdot {{{\mathit{\boldsymbol{\hat{e}}}}}_{\mathit{x}}}=-\iint\limits_{\mathit{S}}{\left( \mathit{p}\rm{-}{{\mathit{p}}_{\infty }} \right){{{\mathit{\boldsymbol{\hat{e}}}}}_{\mathit{x}}}\cdot \rm{d}\mathit{S}} $ |
黏性阻力计算如下:
| $ {\mathit{D}_{\rm{f}}}{\rm{ = }}\mathit{q}{\mathit{S}_{\rm{w}}}{\mathit{C}_{\rm{f}}} $ |
其中q=ρ∞c∞2/2为来流动压, Cf为黏性阻力系数.
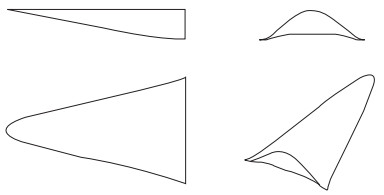
以协和号飞机的机翼参数作为参考, 首先进行初步的计算和筛选, 然后采用均匀设计实验方法[23-24], 以特定大后掠角为目标, 优选出合理的参数组合, 最终得到了符合要求的乘波体.乘波体外形的三视图和侧视图见图 4.
|
| 图 4 宽速域乘波体外形示意图 Fig.4 Diagram of wide speed waverider configuration |
设计参数见表 1.
| 下载CSV 表 1 宽速域乘波体设计参数 Tab.1 Design parameters of wide speed waverider |
Wilcox k-ω模型是为克服k-ε模型的固有缺陷而提出的, 是积分到壁面的两方程涡黏性模型, 通过求解湍动能和它的比耗散率的对流输运方程确定涡黏性系数[25-26].在原始模型的基础上, 可以进行可压缩修正、长度尺度修正和低Reynolds数修正, 下面介绍其具体表达形式.
湍动能k和比耗散率ω的输运方程为
| $ \begin{array}{l} \frac{{\partial \left( {\mathit{\bar \rho k}} \right)}}{{\partial \mathit{t}}}{\rm{ + }}\frac{\partial }{{\partial {\mathit{x}_\mathit{j}}}}{\rm{(}}\mathit{\tilde p}{{\mathit{\tilde u}}_\mathit{j}}\mathit{k}{\rm{) = }}\frac{\partial }{{\partial {\mathit{x}_\mathit{j}}}}\left( {{\rm{(}}{\mathit{\mu }_{\rm{l}}}{\rm{ + }}{\mathit{\sigma }_\mathit{k}}{\mathit{\mu }_{\rm{t}}}{\rm{)}}\frac{{\partial \mathit{k}}}{{\partial {\mathit{x}_\mathit{j}}}}} \right){\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{P}_\mathit{k}}{\rm{ - }}\mathit{ \bar \rho }{\mathit{\beta }_\mathit{k}}\mathit{k\omega }\\ \frac{{\partial \left( {\mathit{\bar \rho \omega }} \right)}}{{\partial \mathit{t}}} + \frac{\partial }{{\partial {\mathit{x}_\mathit{j}}}}{\rm{(}}\mathit{\tilde p}{{\mathit{\tilde u}}_\mathit{j}}\mathit{\omega }{\rm{) = }}\frac{\partial }{{\partial {\mathit{x}_\mathit{j}}}}\left( {{\rm{(}}{\mathit{\mu }_{\rm{l}}}{\rm{ + }}{\mathit{\sigma }_\mathit{\omega }}{\mathit{\mu }_{\rm{t}}}{\rm{)}}\frac{{\partial \mathit{\omega }}}{{\partial {\mathit{x}_\mathit{j}}}}} \right){\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\gamma }\frac{\mathit{\omega }}{\mathit{k}}{\rm{\cdot}}{\mathit{P}_\mathit{k}}{\rm{ - }}\mathit{\bar \rho }{\mathit{\beta }_\mathit{\omega }}{\mathit{\omega }^{\rm{2}}} \end{array} $ |
其中, Pk为湍动能k的生成项.
涡黏性系数定义为湍动能k和比耗散率ω的函数:
| $ {\mathit{\mu }_{\rm{t}}}{\rm{ = }}\mathit{\bar \rho k}{\rm{/}}\mathit{\omega } $ |
k-ε模型也有其固有缺陷, 即在计算自由剪切层流动时显著依赖于ω的自由来流值, 而k-ε模型则无此现象, 为此Menter提出了Menter SST模型, 其基本思想就是在近壁区保留k-ω模型具有的鲁棒性和高精度, 同时利用k-ε模型在边界层外缘与自由来流无关的特点.为了实现这一思想, Menter将k-ε模型转化为k-ω模型, 转化形式与原始k-ω模型的差别在于ω方程右端多了交叉扩散项, 且方程的系数不一样.在Menter k-ω SST模型中, 涡黏系数被重新定义为[27-28]:
| $ {\mathit{\mu }_{\rm{t}}}{\rm{ = }}\frac{{\mathit{\rho k}}}{{{\rm{max(}}\mathit{\omega }{\rm{, }}\mathit{\Omega }{\mathit{F}_{\rm{2}}}{\rm{/}}{\mathit{a}_{\rm{1}}}{\rm{)}}}} $ |
Ω=|Ω|为涡量值.开关函数F2在边界层流动中趋于1, 在自由剪切层流动中趋于0.
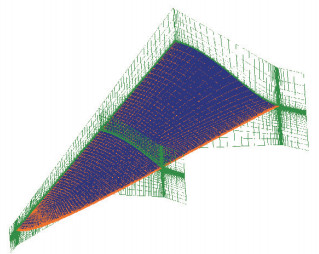
3 乘波体的高速气动特性 3.1 网格生成及计算条件为了加速收敛, 提高计算的精度和效率, 计算采用结构网格, H型拓扑结构, 在壁面邻域进行了加密, 半模网格量约为7.2×105.生成的网格如图 5所示.
|
| 图 5 高速计算网格 Fig.5 High speed calculation grids |
计算攻角α=-2~10°, 间隔2°, 不考虑侧滑.由于模型是对称的, 所以仅对半模进行计算, 并考虑3个方向的黏性.计算条件参数见表 2.
| 下载CSV 表 2 高速计算条件 Tab.2 Parameters of high speed calculation conditions |
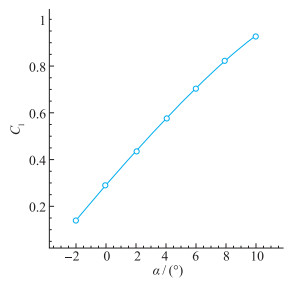
升力系数的曲线如图 6所示, 可以看出攻角在-2~4°的范围内, Cl呈线性变化.这是由于攻角增大时, 下表面的气体受到压缩的程度更加剧烈, 而上表面继续近似保持为自由来流平面, 压强变化较小, 这使得上下表面的压力差更大, 升力也更大.这与超声速空气动力学的小扰动线化理论是相符的[24].当攻角继续增大时, 升力系数斜率有减小的趋势.这主要是因为下表面激波开始下移, 不再依附在前缘上, 上下表面的溢流严重, 造成升力增量的减小, 升力线斜率开始下降.
|
| 图 6 M=6时升力系数曲线 Fig.6 Lift coefficient curve when M=6 |
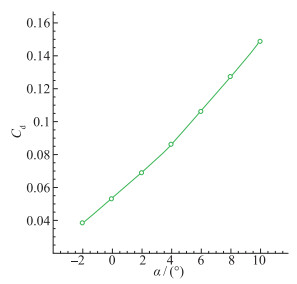
阻力系数Cd和升力系数变化趋势相同, 见图 7, 都随攻角增大而增大, 但显然阻力系数的增长趋势更为明显.在高Mach数的情况下, 飞行器的阻力主要由激波阻力主导.在设计状态附近, 激波紧紧依附在乘波体的前缘, 此时的激波阻力是很小的, 阻力系数大约为0.05.而攻角增大改变了激波的附体特性, 气体开始出现分离的迹象, 使得波阻增加.另一方面, 乘波体的边界层变厚, 黏性阻力也明显增大, 所以总的阻力增长很快.
|
| 图 7 M=6时阻力系数曲线 Fig.7 Drag coefficient curve when M=6 |
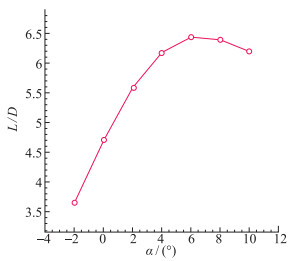
从图 8升阻比曲线可以看出, 升阻比随攻角的变化先增加后减小, 在临界攻角αc =6°乘波体达到最大升阻比(L/D)max=6.422.可以看出, 乘波体并非在设计状态(即α=0°)时升阻比最大.当攻角大于0时, 虽然乘波体的乘波特性受到干扰, 但气流在上表面加速膨胀, 在下表面受到压缩, 使得升阻比继续增加.当攻角过大时, 从下表面泄露到上表面的高压气体已经造成相当的影响, 此时升力增长趋势变缓, 而压差阻力迅速增大, 造成升阻比的下降.在较小正攻角2~8°的范围内, 乘波体的升阻比变化平缓, 而且保持在较高的数值, 气动特性能够满足巡航要求.
|
| 图 8 M=6时升阻比曲线 Fig.8 Lift-drag ratio curve when M=6 |
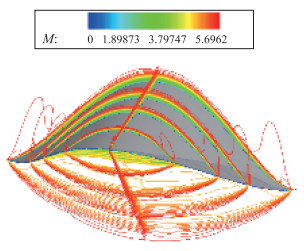
设计状态(α=0°)下的流场Mach数等值线如图 9所示, 可以看出, 乘波体上表面为自由来流面, 除了乘波体头部流动有小幅波动外, 其他部位都被自由来流紧紧包裹着.由于黏性效应, 上表面还贴着一层边界层, 其厚度从前缘向乘波体中部逐渐增大.在乘波体的下表面, 激波依附在前缘上, 构成了典型的乘波效应.黏性的存在使得前缘有小部分的溢流, 但等值线过渡很平缓, 说明溢流是很小的.激波与下表面之间流动近似为锥形流动, 流场还是比较均匀.从上面也可以知道, 乘波体在设计状态的阻力很小, 升阻比在3.65左右.总体而言, 涡升力乘波体能很好地满足乘波体的特性, 符合巡航状态的高升阻比要求.
|
| 图 9 设计状态时Mach数等值线图 Fig.9 Mach number contour diagram in design state |
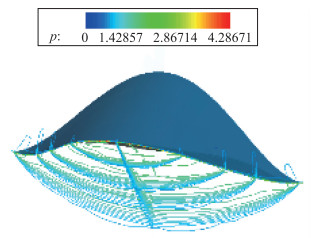
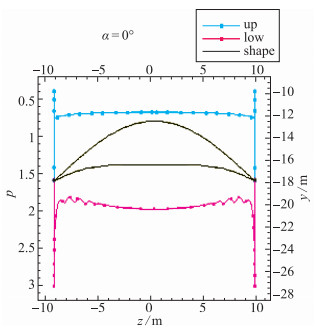
图 10和图 11分别给出了乘波体的压力等值线图和中截面的压强分布.从这两个图可以得到, 下表面压强要高于上表面压强.其中, 上表面压强分布均匀, 与来流静压相等.而下表面出现中间高、两边低的特征, 但是差别不是很大.在靠近前缘的地方, 有一定的波动, 说明乘波体前缘对流动的影响还是有的.从压力分布图可以发现, 前缘的压力大概为上表面和下表面的均值, 这表明下表面的高压气体在前缘被很好地拦截了, 没有对上表面的低压区造成大的污染, 也就是说, 溢流是不明显的.这也说明, 下表面激波能很好地附着在前缘上.
|
| 图 10 设计状态时压力等值线图 Fig.10 Pressure contour diagram in design state |
|
| 图 11 设计状态时中截面压力分布 Fig.11 Pressure distributions of middle section in design state |
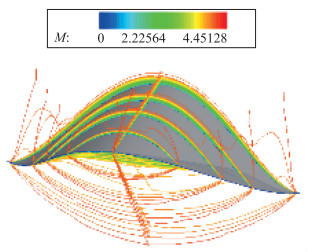
取攻角α=-2°分析乘波体在负攻角的流场细节.全流场的Mach数等值线如图 12所示.当乘波体以负攻角飞行时, 气流在上表面的流动就受到压缩, 产生弱激波.随着攻角绝对值的增大, 激波会越来越强, 直至成为脱体激波, 从而改变乘波特性.从流场图可以看出, 气流上扬的趋势很明显, 在头部已经引出一道激波.边界层厚度也有所增加.而下表面激波位置开始下移, 并且变弱(等值线变疏), 从等值线的发散程度来看, 前缘处的溢流已经非常明显.
|
| 图 12 负攻角(α=-2°)时Mach数等值线图 Fig.12 Mach number contour diagram when α=-2° |
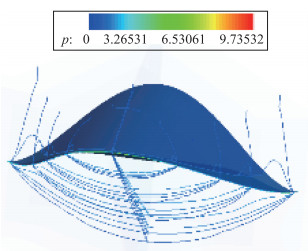
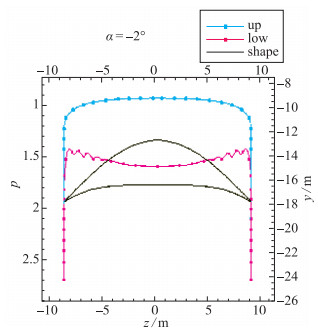
压力等值线和中截面压力分布如图 13和图 14所示.可以看到, 乘波体的上表面压力增加, 而下表面压力减小.上表面压力增加的原因是上表面气流受到压缩, 来流一部分的动压转化为静压.下表面压力减小主要是由于激波的位置下移和强度变弱, 与设计状态比较, 其压力减小是非常明显的, 这直接导致升力的减小.在中截面压力分布值中也可以看到, 上表面在前缘处的压力没有先减小后增加的趋势, 也就是对流区转移到了下表面.而且, 前缘处的压力值比下表面压力值还要大, 这说明, 激波已经开始不附着在前缘上了.整体来看, 负攻角对乘波特性的破坏程度是很严重的.
|
| 图 13 负攻角状态(α=-2°)时压力等值线图 Fig.13 Pressure contour diagram when α=-2° |
|
| 图 14 负攻角状态(α=-2°)时中截面压力分布 Fig.14 Pressure distributions of middle section when α=-2° |
从气动分析可以发现, 乘波体的升阻比在攻角α=4°附近获得了很高的数值, 而在攻角α=10°就已经下降了.当攻角为α=10°时, 乘波体全流场的Mach数等值线如图 15所示.从图中可以看到, 上表面气流膨胀加剧, 边界层在对称面和前缘处很薄, 而在靠近对称面处(约为10%~25%)边界层变厚, 出现了分离的迹象.而下表面的激波强度增大, 激波位置更加靠近壁面, 流动不再是锥形流动.此时, 虽然前缘处的对流加剧, 但激波大抵还是吸附在前缘上的.总的来说, 就是上表面“膨胀不足”, 下表面“压缩有余”, 流场发生了畸变.

|
| 图 15 攻角α=10°时Mach数等值线图 Fig.15 Mach number contour diagram when α=10° |
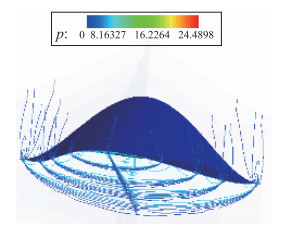
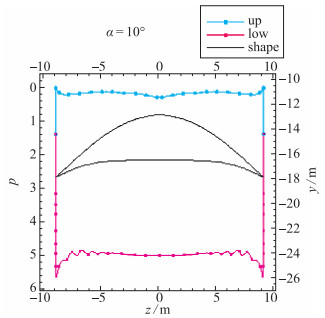
图 16和图 17给出了压力等值线和中截面压力分布图, 可以看出前缘处的压力依旧处于上下表面压力之间, 且偏向于低压.上表面在前缘和对称面之间出现了局部低压, 这是边界层变厚的原因.在前缘处, 对流的情况加剧, 更多的高压气体迁移到上表面.较前一状态, 上表面压力减少微弱, 下表面压力增加明显, 总的升力还是增加的.但是由于大攻角使流场发生了畸变, 导致了升阻比的下降.
|
| 图 16 攻角α=10°时压力等值线图 Fig.16 Pressure contour diagram when α=10° |
|
| 图 17 攻角α=10°时中截面压力分布 Fig.17 Pressure distributions of middle section when α=10° |
计算采用结构网格.与高速网格类似, 主要采用H型拓扑.为保证低速时的远场特性, 外场长度约为乘波体长度的20倍.网格总量约3.6×106.生成的网格如图 18所示.

|
| 图 18 低速计算网格 Fig.18 Low velocity calculation grids |
使用流体力学工具, 对乘波体在攻角α=0~25°, 间隔5°进行了计算.不考虑侧滑和换热效应.低速计算条件参数见表 3.
| 下载CSV 表 3 低速计算条件参数 Tab.3 Parameters of low velocity calculation conditions |
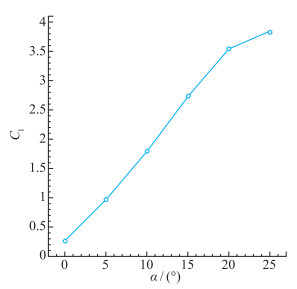
乘波体在M=0.3时的升力系数随攻角的变化如图 19所示.升力曲线在0~15°攻角范围内近乎是线性的, 但当α=0°时, 升力系数很小, 这是由于在攻角为零时, 涡还未产生, 而乘波体前缘很锋利, 气流如同流过夹角很小的楔形体, 上下表面的压强差很小, 所以升力也小.攻角增加后, 涡的强度也增加, 对上表面的影响区域变大, 升力也随着增大.当α≥20°时, 升力线斜率开始下降.这是由于涡开始破裂, 涡诱导产生的附加升力逐渐减弱.
|
| 图 19 低速时升力系数曲线 Fig.19 Lift coefficient curve at low velocity |
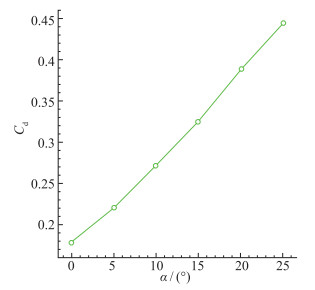
图 20给出了低速时的阻力系数曲线, 与高速的情况类似, 随着攻角增加, 阻力呈一直增长的趋势, 开始的时候增长慢, 后来增长快. α=0°时的阻力为摩擦阻力, 阻力系数在0.15左右, 这个值是很小的, 对总阻力的影响微乎其微.所以, 是涡的诱导阻力在起主导作用.当涡增强时, 除了改变上表面压力分布外, 还影响着乘波体后场的流场特性.在黏性作用下, 诱导阻力快速增加, 攻角越大就越明显.
|
| 图 20 低速时阻力系数曲线 Fig.20 Drag coefficient curve at low velocity |
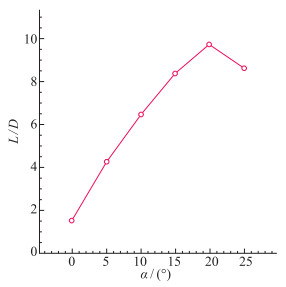
乘波体的升阻比曲线见图 21.升阻比随攻角的变化是先增加后减小, 当攻角αc=20°时, 乘波体达到最大升阻比(L/D)max=9.737.普通飞机的升阻比大约为7~20, 由此看来这个升阻比是非常可观的.在平飞状态也就是α=0°时, 乘波体不光升力阻力小, 而且升阻比很小, 这个时候的气动特性很差.只有攻角达到10°以上时, 涡的位置和强度才较为理想, 产生的附加升力使升阻比的数值稳定在6以上.而当攻角大于25°时, 涡开始破碎, 气体出现分离, 从而导致升阻比的下降.
|
| 图 21 低速时升阻比曲线 Fig.21 Lift-drag ratio curve at low velocity |
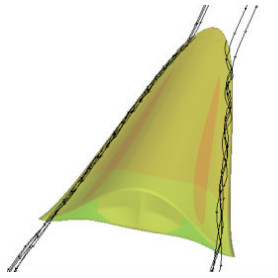
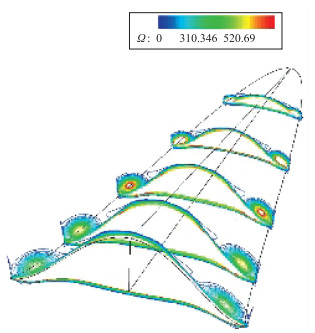
当α=0°时, 只在前缘处生成两股细小的对称涡.此时, 涡的强度很弱, 对上表面的影响也很小. 图 22给出了流线图, 图 23给出了涡量的截面图.从这两个图可以看出, 涡在上表面不远处, 强度不大, 影响的范围很小.
|
| 图 22 攻角α=0°时流线图 Fig.22 Vortex and streamline diagram when α=0° |
|
| 图 23 攻角α=0°时涡量等值面图 Fig.23 Section diagram of vorticity when α=0° |
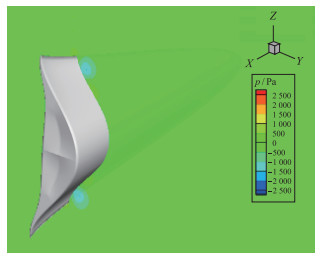
为了更好地捕捉流场的变化, 在靠近乘波体底部(x=9 m)处截取了压力云图和压力分布图, 分别如图 24和图 25所示.可以看到, 除了涡在上表面诱导产生的一小部分低压区外, 上下表面压强几乎没有差别, 也就是说, 总体流场非常均匀.此时, 乘波体升力很小, 阻力相对升力而言较大, 乘波体的气动特性是不佳的.
|
| 图 24 攻角α=0°时截面x=9 m压力云图 Fig.24 Pressure cloud diagram at x=9 m when α=0° |

|
| 图 25 攻角α=0°时截面x=9 m压力分布 Fig.25 Pressure distributions diagram at x=9 m when α=0° |
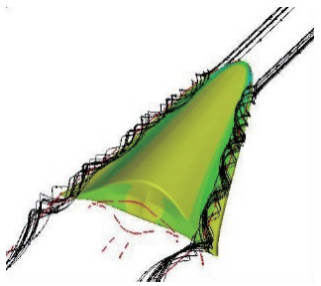
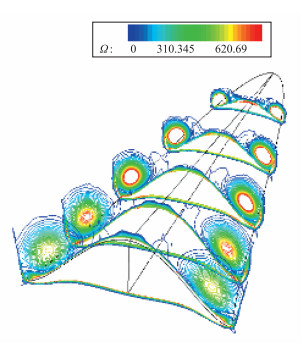
当攻角α=10°时, 在乘波体的背风面出现了典型的对称涡. 图 26给出了涡核和流线图, 红色线表示涡核, 可以看出涡跟随着前缘曲线向后伸展, 在上表面产生了低压区, 从而产生涡升力. 图 27给出了乘波体的涡量等值面图, 可以看出, 涡的结构是很明显的.相对于α=0°, 涡的强度增大, 位置升高, 影响区域也在逐渐扩大.
|
| 图 26 攻角α=10°时涡核及流线图 Fig.26 Vortex and streamline diagram when α=10° |
|
| 图 27 攻角α=10°时涡量等值面图 Fig.27 Section diagram of vorticity when α=10° |
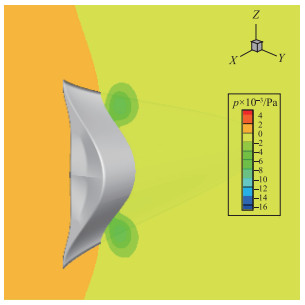
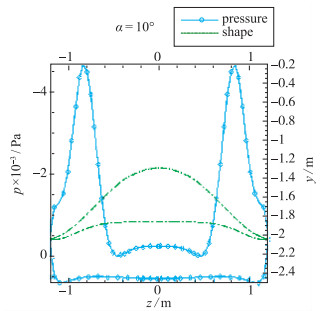
图 28和图 29给出了乘波体x=9 m处的压力云图和压力分布图.可以看到, 下表面压力变化很平坦, 而上表面除了涡产生两部分局部低压外, 变化也是很平缓的.与前一状态比较, 上下表面压强有了明显的分界线.在压力分布图中看到了两个尖峰, 说明涡诱导的强低压区吸附在上表面上, 产生的附加升力很明显.从气动特性曲线知道, 此时乘波体的升阻比大约为6.5, 这和涡的作用是密切相关的.
|
| 图 28 攻角α=10°时截面x=9 m压力云图 Fig.28 Pressure cloud diagram at x=9 m when α=10° |
|
| 图 29 攻角α=10°时截面x=9 m压力分布 Fig.29 Pressure distributions diagram at x=9 m when α=10° |
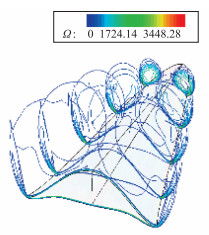
图 30及图 31分别为乘波体的涡量图和涡量等值面图.随着攻角的增加, 涡的强度在增加, 位置也在抬高, 在上表面产生低压区也越来越明显, 这对提高乘波体的升阻比是很有利的.然而, 当攻角到达25°时, 诱导产生的涡除了在头部的小部分区域还能保持完整外, 就开始逐渐破碎了.下面的涡量图和截面图表明了这一点, 可以看到在靠近底面的时候涡量曲线已显得非常凌乱.在气动分析中, 发现此时升阻比已经开始下降.这说明大攻角下会导致涡的破裂, 进而影响乘波体的气动性能.

|
| 图 30 攻角α=25°时涡量图 Fig.30 Vorticity diagram when α=25° |
|
| 图 31 攻角α=25°时涡量等值面图 Fig.31 Section diagram of vorticity when α=25° |
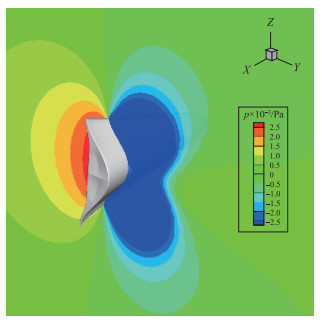
图 32和图 33给出了乘波体x=9 m处的压力云图和压力分布图.可以看到, 在大攻角下, 下表面附近受压形成较均匀的高压区, 而上表面涡已经开始分离, 气体加速膨胀形成低压区, 仅仅在靠近对称面处还保留一部分的高压.这样升力虽然也在增加, 但压差阻力增加更为剧烈, 造成了升阻比的下降.
|
| 图 32 攻角α=25°时截面x=9 m压力云图 Fig.32 Pressure cloud diagram at x=9 m when α=25° |

|
| 图 33 攻角α=25°时截面x=9 m压力分布 Fig.33 Pressure distribution diagram at x=9 m when α=25° |
乘波体是高超声速飞行器极有前景的外形之一, 但目前大多数乘波体在低速情况下的气动特性不佳.本文提出了一种思路, 通过精确控制前缘和后掠角, 使乘波体在低速条件下可以利用大后掠前缘涡增加升力, 以改善其低速气动性能.通过对获得的宽速域乘波体高速和低速的气动性能计算和流场分析, 得到一些有意义的结论:
(1) 乘波体在设计条件下激波贴附在前缘上, 能够很好地满足乘波特性.负攻角的存在使下表面附体激波变弱, 上表面产生激波, 从而破坏乘波特性, 导致气动特性恶化.正攻角的情况下, 随着攻角的增加, 上表面气体膨胀, 下表面激波增强, 气体受到压缩程度加剧, 在一定范围内气动特性会优于设计状态.当攻角继续增加时, 上下表面在前缘处的对流加剧, 上表面气体膨胀过度出现分离, 使得升阻比下降.
(2) 低速的条件下, 在攻角为零时就开始在前缘处形成对称的涡结构.随着攻角的增加, 涡的强度增加, 位置抬高, 在上表面诱导产生的低压区范围也不断扩大, 使得升力和升阻比上升, 这非常有利于改善乘波体的低速气动特性.但当攻角增加到一定范围以后, 涡结构从底部开始破裂, 导致气流分离, 从而抹平上表面的吸力峰, 造成气动特性的恶化.
| [1] |
黄志澄, 仇强华, 袁生学. 高超声速飞行展望[J]. 流体力学实验与测量, 1997, 11(1): 6-11. Huang Z C, Qiu Q H, Yuan S X. Prospect of hypersonic flight[J]. Experiments and Measurements in Fluid Mechanics, 1997, 11(1): 6-11. (in Chinese) |
| [2] |
Starkey R P, Lewis M J. Analytical off-design lift-to-drag-ratio analysis for hypersonic waveriders[J]. Journal of Spacecraft and Rockets, 2000, 37(5): 684-691. DOI:10.2514/2.3618 |
| [3] |
Wang Y, Zhang D, Deng X. Design of waverider configuration with high lift-drag ratio[J]. Journal of Aircraft, 2007, 44(1): 144-148. DOI:10.2514/1.22669 |
| [4] |
Starkey R P, Lewis M J. Simple analytical model forparametric studies of hypersonic waveriders[J]. Journal of Spacecraft and Rockets, 1999, 36(4): 516-523. DOI:10.2514/3.27194 |
| [5] |
Lin S C, Luo Y S. Optimization of waverider generated from conical flow with combined transverse and longitudinal curvature[C]. 13th Applied Aerodynamics Conference, San Diego, 1995:1849.
|
| [6] |
Zhang J, Wang F M. Hypersonic waveriders aerodynamic performance studies[J]. Journal of Astronautics, 2007, 28(1): 203-208. |
| [7] |
Sobieczky H, Dougherty F C, Jones K. Hypersonic waverider design from given shock waves[C]. Proceedings of the First International Hypersonic Waverider Symposium, Maryland, 1990:17-19.
|
| [8] |
Takashima N, Lewis M. Waverider configurations based on non-axisymmetric flow fields for engine-airframe integration[R]. AIAA 1994-0380, 1994.
|
| [9] |
Rasmussen M L, Clement L W. Cone-derived waveriders with longitudinal curvature[J]. Journal of Spacecraft and Rockets, 1986, 23(5): 461-469. DOI:10.2514/3.25830 |
| [10] |
Huang W, Ma L, Wang Z G, et al. A parametric study on the aerodynamic characteristics of a hypersonic waverider vehicle[J]. Acta Astronautica, 2011, 69(3/4): 135-140. |
| [11] |
He X, Rasmussen M L. Computational analysis of off-design waveriders[J]. Journal of Aircraft, 1994, 31(2): 345-353. DOI:10.2514/3.46493 |
| [12] |
Mazhul I I, Rakhimov R D. Hypersonic power-law shaped waveriders in off-design regimes[J]. Journal of Aircraft, 2004, 41(4): 839-845. DOI:10.2514/1.386 |
| [13] |
Takashima N, Lewis M J. Optmization of waverider-based hypersonic cruise vehicles with off-design considerations[J]. Journal of Aircraft, 2015, 36(1): 235-245. |
| [14] |
Rodi P E. Vortex lift waverider configurations[R]. AIAA 2012-1238, 2012.
|
| [15] |
Rodi P E. Geometrical relationships for osculating cones and osculating flowfield waveriders[R]. AIAA 2011-1188, 2011.
|
| [16] |
王发民, 丁海河, 雷麦芳. 乘波布局飞行器宽速域气动特性与研究[J]. 中国科学E辑:技术科学, 2009, 39(11): 1828-1835. Wang F M, Ding H H, Lei M F. Aerodynamic characteristics research on wide, speed range waverider configura-tion[J]. Science in China Series E:Technological Sciences, 2009, 39(11): 1828-1835. (in Chinese) |
| [17] |
李世斌, 罗世彬, 黄伟, 等. 新型宽速域高超声速飞行器气动特性研究[J]. 固体火箭技术, 2012, 35(5): 588-592. Li S B, Luo S B, Huang W, et al. Investigation on aerodynamic performance for a novel wide-ranged hypersonic vehicle[J]. Journal of Solid Rocket Technology, 2012, 35(5): 588-592. (in Chinese) |
| [18] |
段焰辉, 范召林, 吴文华. 定后掠角密切锥乘波体的生成和设计方法[J]. 航空学报, 2016, 37(10): 3023-3034. Duan Y H, Fan Z L, Wu W H. Generation and design methods of osculating cone waverider with constant angle of sweepback[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 3023-3034. (in Chinese) |
| [19] |
甘文彪, 阎超, 耿云飞, 等. 乘波飞行器一体化构型设计[J]. 空气动力学学报, 2012, 30(1): 68-73. Gan W B, Yan C, Geng Y F, et al. Waverider design of integrated configuration[J]. Acta Aerodynamica Sinica, 2012, 30(1): 68-73. (in Chinese) |
| [20] |
Liao J R, Isaac K M, Miles J B, et al. Navier-Stokes simulation for cone-derived waverider[J]. AIAA Journal, 1992, 30(6): 1521-1528. DOI:10.2514/3.11096 |
| [21] |
Lin S C, Rasmussen M L. Cone-derived waverider with combined transverse and longitudinal curvature[R]. AIAA 1988-371, 1988.
|
| [22] |
张东俊, 王延奎, 邓学蓥. 高升阻比乘波体外形设计及气动特性计算研究[J]. 北京航空航天大学学报, 2004, 30(5): 429-433. Zhang D J, Wang Y K, Deng X Y. Design and computational study of waverider configuration with high performance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(5): 429-433. (in Chinese) |
| [23] |
Wang Z J, Luo D H, Ena C. Optimization of polysaccharides extraction from Gynostemma pentaphyllum Makino using uniform design[J]. Carbohydrate Polymers, 2007, 69(2): 311-317. DOI:10.1016/j.carbpol.2006.10.013 |
| [24] |
李响, 李为吉, 彭程远. 基于均匀实验设计的响应面方法及其在无人机一体化设计中的应用[J]. 机械科学与技术, 2005, 24(5): 575-577. Li X, LI W J, Peng C Y. Response surface methodology based on uniform design and its application to complex engineering system optimization[J]. Mechanical Science and Technology, 2005, 24(5): 575-577. (in Chinese) |
| [25] |
Wilcox D C. Reassessment of the scale-determining equation for advanced turbulence models[J]. AIAA Journal, 1988, 26(11): 1299-1310. DOI:10.2514/3.10041 |
| [26] |
Wilcox D C. Formulation of the k-ω turbulence model revisited[J]. AIAA Journal, 2008, 46(11): 2823-2838. DOI:10.2514/1.36541 |
| [27] |
Menter F R. Zonal two equation k-ω turbulence models for aerodynamic flows[R]. AIAA 1993-2906, 1993.
|
| [28] |
Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |



