2. 西北工业大学翼型叶栅空气动力学国家重点实验室,陕西西安 710072
2. National Key Laboratory of Science and Technology on Aerodynamic Design and Research, Northwestern Polytechnical University, Xi'an 710072, China
随着计算机技术和流场测量技术的高速发展, 研究者获得流场数据越来越便利, 也越来越精细[1-2].与此同时, 面对海量数据, 高效地处理分析数据, 获取有用信息, 以支撑未来飞行器设计发展, 逐渐成为了研究热点.目前, 基于数据驱动的数据挖掘和机器学习等技术成为了处理和分析数据的主要途径.基于特征提取的本征正交分解方法(proper orthogonal decomposition, POD)作为一种高效的降阶方法, 已在流场数据信息提取[3-4]和非定常流场动力学分析[5-7]等方面得到了广泛应用.
POD方法[8]的主要思路是寻找一组最佳的标准正交基, 使得样本数据在该标准正交基上的投影依次迅速递减, 截取投影较大或者说包含能量较高的前几阶模态, 从而可以用较少的基展开获得较高阶数据的近似描述.该方法已成功应用于诸多领域, 如图像处理, 信号分析和数据压缩等[9].在流体力学领域, POD方法主要有两方面的应用.一是用于特征模态的提取. Lumley[10]首先将POD方法引入了湍流领域, 用于提取湍流的主要特性或拟序结构.魏斌斌等[11]将POD方法引入高超声速脉动压力数据处理中, 发展了基于POD方法的高超声速边界层转捩判定方法.李卓越等[12]将POD方法应用于实验测量数据的分解, 分析了受激后向台阶分离流的流场特性.二是用于构建气动力降阶模型. Deane等[13]结合Galerkin投影的方法, 成功使用基于POD方法的降阶模型预测了槽道流和圆柱绕流的极限环行为.基于POD方法的降阶模型与结构模型进行耦合, 可以实现气动弹性的快速预测[14], 如颤振特性分析[15-17]、极限环预测[18-19]以及气动弹性主动控制律设计[20-21]等.在保证计算精度的前提下, 极大地提高了计算效率.另外, POD方法在气动外形优化[22]、气动外形反设计[23]和流动控制[24]等方面也得到了应用.
Everson等[25]针对不完整样本或缺失流场, 在基本POD方法的基础上, 发展了Gappy POD方法.给定一组POD模态, 一个不完整流场快照可以通过求解一组线性方程组得以重构.并且, 如果用于求解POD模态的样本存在数据缺失, 那么可以通过迭代的方法实现缺失流场重构.该方法已成功应用于不完整人脸图像的重构.对于流体力学问题, 几种情况可能导致数据的不完整.首先, 实验中可能只得到了某些点的测量值, Gappy POD方法就可以通过这些已知点重构出完整流场的数据[26].其次, 流场的某些数据是未知的.例如, 已知一组翼型形状和其相对应的流场解, 给定一个新的翼型形状, 这时, 通过Gappy POD方法可以快速估算出新翼型对应的流场解[27].另外, Gappy POD方法还可以应用于翼型反设计问题[28-29].本文在上述应用的基础上针对Gappy POD方法在数据填补应用中可能会遇到的数据集缺失情况以及重构过程中的参数选择问题开展研究, 以期为Gappy POD方法在缺失流场数据填补方面的应用提供较为全面的参考经验.
本文以非定常圆柱绕流流场作为样本数据, 针对样本数据已知和不完全已知两种情况, 探究了模态阶数、缺失率以及样本数对缺失流场重构精度的影响规律.结果表明, 两种情况下, Gappy POD方法均能以较少阶模态高精度再现完整流场.另外, 在样本缺失率较高的情况下, 可适当增加样本数以提高重构精度.
1 Gappy POD方法 1.1 适用于缺失流场重构的Gappy POD方法Gappy POD方法是POD方法的一种变形, 用于填补流场中的缺失数据.在获得某个参数范围内的一系列采样解后, 采用Gappy POD方法可以填补该参数范围内任意参数值下的缺失数据.
首先建立一个“标签”向量, 用以描述所需重构的流场中每个位置上的数据是已知还是缺失.对于流场解Uk, 其相应的标签向量nk定义如下:如果Uik(Uik代表流场解向量Uk中的第i个元素)缺失或不正确, 则nik=0;如果Uik已知, 则nik=1.为方便起见, 将解向量Uk中缺失或不正确的元素通过点乘(nk, Uk)i=nikUik置为零.内积定义为(u, v)n=[(n, u), (n, v)], 相应的模定义为(||v||n)2=(v, v)n.
设{Φi}i=1m为一组样本集{Ui}i=1m的POD基, 样本集中的所有快照均完整已知.设g为样本参数范围内具有一部分缺失数据的流场解向量, 其对应的标签向量为n.假设g为需要重构或填补的解向量, 且该解向量的流场特征可以由上述样本集的POD基表示, 则由前p阶POD基表示的重构解向量可表示为
| $ \mathit{\boldsymbol{\tilde g}} \approx \sum\limits_{i = 1}^p {{b_i}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^i} $ | (1) |
定义原始流场解向量与重构解向量的误差为
| $ E = \left\| {\mathit{\boldsymbol{g}} - \mathit{\boldsymbol{\tilde g}}} \right\|_n^2 $ | (2) |
通过保证该误差最小以求得模态系数.为保证E最小, 可以将式(2)对各阶模态系数bi求导, 从而得到如下线性方程组
| $ \mathit{\boldsymbol{Mb}} = \mathit{\boldsymbol{f}} $ | (3) |
式中,Mij=(Φi, Φj)n, fi=(g, Φi)n.求解式(3)得到b, 并带入式(1), 得到重构流场解向量
上述Gappy POD方法可以延伸到样本集不完全已知的情况, 在这种情况下, POD基可以通过迭代的方法得到, 该方法由Everson和Sirovich提出.设一组不完整的样本集{gk}k=1m, 相对应的标签矩阵为{nk}k=1m.首先将样本中的缺失元素用其余样本在该点的平均值代替, 如下
| $ h_i^k(0) = \left\{ {\begin{array}{*{20}{l}} {g_i^k,}&{n_i^k = 1}\\ {{{\tilde g}_i},}&{n_i^k = 0} \end{array}} \right. $ |
式中
| $ {\tilde g_i} = \frac{1}{{{P_i}}}\sum\limits_{k = 1}^m {g_i^k} ,\quad {P_i} = \sum\limits_{k = 1}^m {n_i^k} $ |
并且, 令hk(l)为原始流场解向量hk第l次内迭代的猜想解向量, 由这些猜想解向量构成的样本集可以得到一组POD基, 这组POD基将用于下一步迭代中不完整快照的更新.由l=0开始, 迭代步骤总结如下
(1) 对样本集{hk(l)}k=1m进行基本POD模态分析, 得到当前迭代步的POD基向量{Φk(l)}k=1m.
(2) 如适用于缺失流场重构的Gappy POD方法所述, 采用前p=n阶POD基向量重构, 以填补样本中的缺失元素.当前迭代步的临时重构解向量为
| $ \widetilde {{\mathit{\boldsymbol{h}}^k}}(l) = \sum\limits_{i = 1}^p {b_i^k} (l){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^i}(l) $ |
(3) 该临时重构解向量用于填补原始解向量中的缺失元素, 构成下一迭代步的临时猜想解向量, 如下
| $ h_i^k(l + 1) = \left\{ {\begin{array}{*{20}{l}} {h_i^k(l),}&{n_i^k = 1}\\ {\widetilde {h_i^k}(l),}&{n_i^k = 0} \end{array}} \right. $ |
(4) 令l=l+1, 进入下一步迭代.
循环上述迭代过程直到达到最大迭代步骤或达到收敛要求, 该迭代过程称为内迭代.令p=n+1, 重复上述内迭代过程, 进入下一循环的主迭代. Gunes等[30]提出, 可以由直接投影得到的模态系数代替上述方法中的模态系数, 这样省去了最小二乘的计算过程, 提高计算效率. Venturi等[31]提出第n次主迭代中的POD模态阶数均可取为p=n, 且给出了外迭代的收敛机制为:当Kpn-Kp0达到最大值时, 外迭代停止, 其中,
| $ {K_{{p_n}}} = \sum\limits_{i = 1}^N {\lambda _{n,j,i}^2} $ |
内迭代的收敛机制为
| $ \frac{1}{{{p_n}}}\sum\limits_{i = 1}^{{p_n}} {\left| {\frac{{{\lambda _{n,j,i}} - {\lambda _{n,j - 1,i}}}}{{{\lambda _{n,j,i}}}}} \right|} < \varepsilon $ |
一般取ε=0.1即可达到较高的收敛精度.
2 算例验证以Re=100的二维圆柱绕流为研究算例, 选择中心格式有限体积法数值求解N-S方程, 得到样本数据.选取足够大的计算域, 从而减小边界条件对流场计算结果的影响.本文的计算域如图 1所示, 入口边界距离圆心20D, 出口边界距离圆心40D.将计算得到的升力系数幅值和阻力系数的均值与文献已有计算结果[32-34]进行了对比, 见表 1.结果表明, 本文采用的数值方法有很高的精度, 是可靠的.
|
| 图 1 计算网格 Fig.1 Computational grids |
| 下载CSV 表 1 Re=100圆柱绕流的升力系数幅值和阻力系数均值对比 Tab.1 Comparison of lift coefficient amplitude and mean value of drag coefficient for flow past a cylinder of Re=100 |
为了验证适用于缺失流场重构的Gappy POD方法的可行性, 本文采用上述圆柱绕流构造缺失流场算例. CFD计算中一个周期保留120个样本点, 文中每间隔2个点取1个点, 即一共有40个采样点, 该40个采样点用来构造POD基.选取该120个样本点中的第20个样本点作为缺失流场, 该点不在40个采样点内, 假设缺失流场中只有圆柱表面的200个点的数据已知.文中以横向速度场为例展示, 其余变量具有相同的规律.
首先,对40个采样点样本集进行POD分析, 得到用于重构缺失流场的POD基.如图 2和3所示, 分别为特征值曲线和前6阶POD模态.从图中可以看出, 特征值是成对出现的, 且各对间近似为指数递减的趋势.模态图关于x轴成对称或反对称, 前两阶模态反映了流场的大尺度特征.
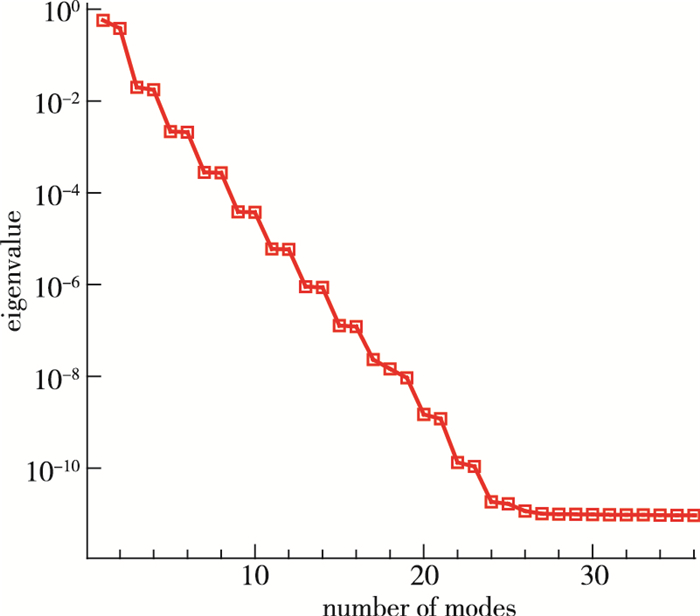
|
| 图 2 特征值曲线 Fig.2 Eigenvalue curve |
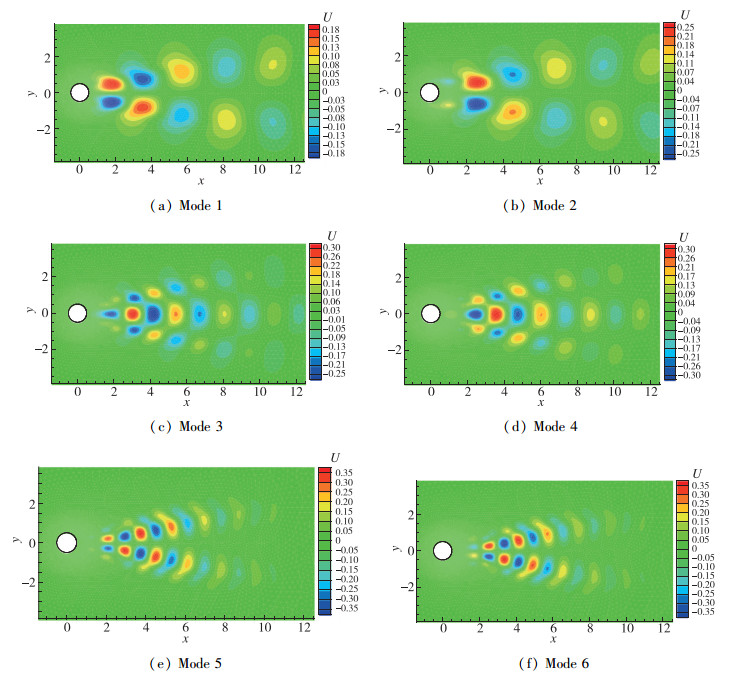
|
| 图 3 前6阶POD模态 Fig.3 POD modes of first six orders |
对缺失流场的横向速度场进行填补, 图 4为使用不同阶POD模态的缺失数据填补结果与CFD计算结果对比图.可以看出, 只使用前2阶模态的填补结果再现了流场的大尺度特征, 缺失流动的小尺度特征.使用前4阶POD模态, 小尺度特征得以体现.当模态阶数增加到10阶时, Gappy POD的填补结果几乎与CFD计算结果完全吻合.为了更直观地显示填补结果与CFD计算结果之间的误差, 文中定义结果误差为
| $ {\rm{error}} = \frac{1}{N}\sum\limits_{i = 1}^N | g_i^{{\rm{ Gappy \;POD }}} - g_i^{{\rm{ CFD }}}| $ |
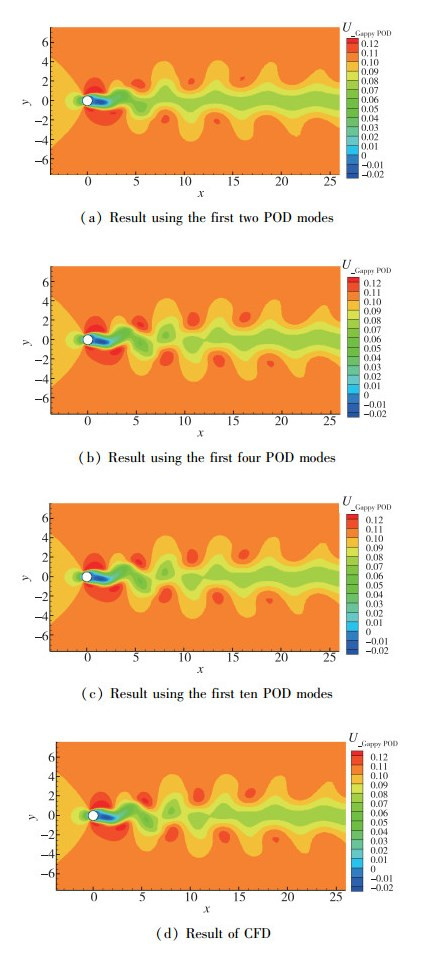
|
| 图 4 POD填补结果与CFD计算结果对比 Fig.4 Comparison of reconstruction data from Gappy POD and original data from CFD |
式中,N表示流场中缺失元素的个数. 图 5为填补的结果误差随所使用的POD模态数的变化曲线, 可以看出, 随着使用POD模态阶数的增加, 填补结果逐渐趋于收敛.
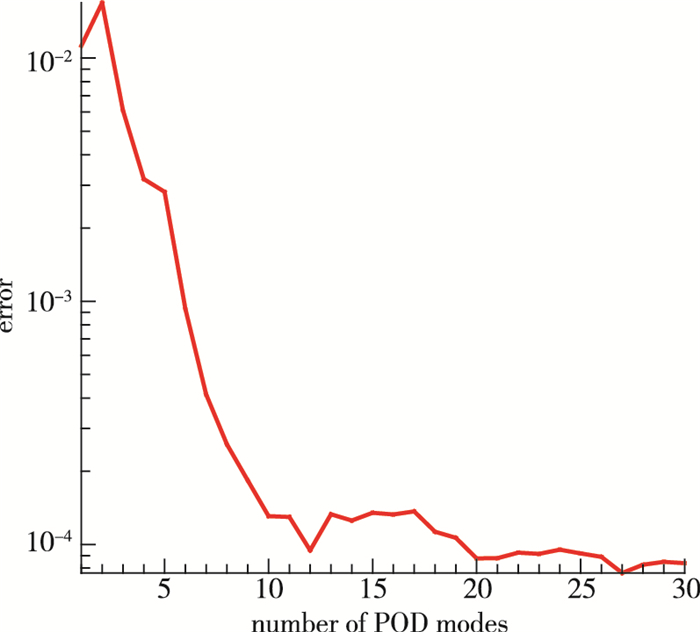
|
| 图 5 误差随重构所用POD模态数的变化曲线 Fig.5 Error versus number of reconstruction modes |
为了构造有数据缺失的流场, 文中在CFD计算得到的完整流场中任意舍弃某些离散点上的数据.为了量化流场中数据的缺失程度, 文中定义未知的离散点个数占总离散点个数的百分比为“缺失率”.采用随机抽样的方式从流场离散点中抽取相应比例的点数, 舍弃其真实值, 作为缺失点.如果取所用样本集的缺失率为某一值, 则样本集中各快照的缺失率在该值附近有微小变化.文中采用各快照的缺失率分布的均值为μ, 方差为σ的正态分布, 其中μ的值等于样本集的缺失率.
仍选择上述Re=100的二维圆柱绕流作为研究算例.下文首先以样本个数40, 空间缺失率20%的算例进行方法的结果展示.各快照缺失率正态分布的均值为0.2, 方差为0.01.为了更直观地显示Gappy POD方法的填补结果与CFD计算结果的误差, 文中定义误差为
| $ {\rm{erro}}{{\rm{r}}_2} = \frac{1}{m}\sum\limits_{j = 1}^m {\frac{1}{{{N_j}}}} \sum\limits_{i = 1}^{{N_j}} | g_i^{{\rm{ Gappy \;POD}}} - g_i^{{\rm{ CFD }}}| $ |
式中,Nj代表第j张快照中缺失元素点的个数. 图 6为该误差随重构所用POD模态阶数的变化曲线, 可以看出, 随着模态阶数的增加, 误差单调递减, 且最终收敛于接近0的值.使用10阶模态, 即外迭代步达到10步, 即可得到较精确的结果.
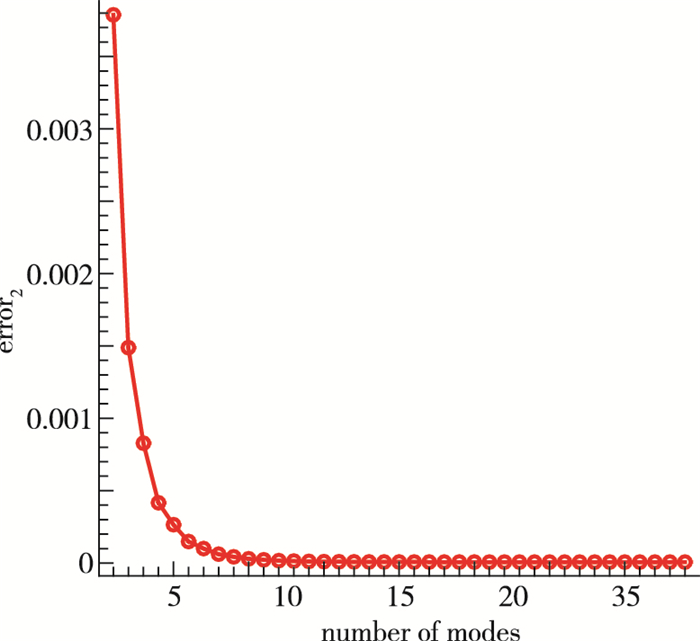
|
| 图 6 误差随重构所用POD模态阶数的变化曲线 Fig.6 Error versus number of reconstruction modes |
图 7为各外迭代步得到的特征值曲线与原始完整样本的特征值曲线对比图.可以看出, 随着迭代步数的增加, 迭代步的特征值曲线逐渐收敛到原始样本的特征值曲线, 且低阶模态的特征值几乎与真实特征值完全吻合.但是随着迭代步数的增加, 收敛速度逐渐减慢, 且高阶模态的特征值与真实特征值相差较大.也就是说, 当迭代步刚开始时, Gappy POD方法首先捕捉到流场的大尺度特征, 随着迭代步数的增加, 逐渐捕捉到流场的细小特征, 对流场的重构也更精细.但是样本中离散点数据的缺失, 导致某些流场特征的丢失, 不能全完复现原始流场的特征.
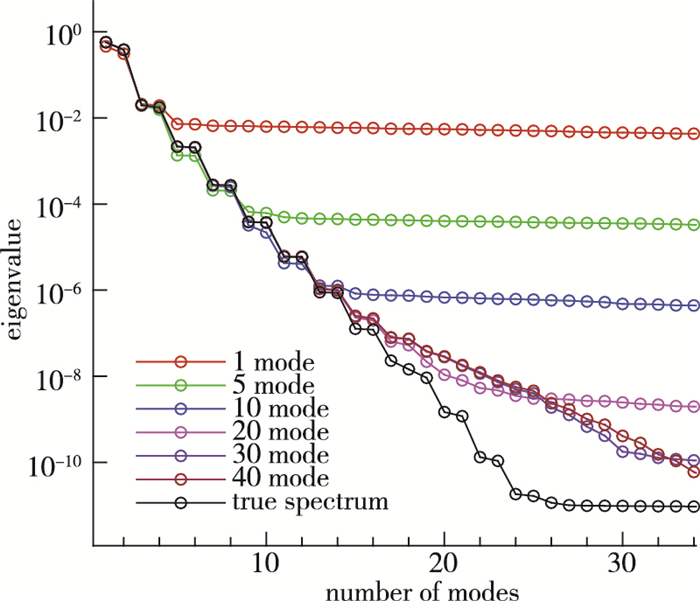
|
| 图 7 各迭代步的特征值曲线与原始样本特征值曲线对比图 Fig.7 Comparison of eigenvalue curves from each iteration steps and original snapshots |
为了测试该方法在不同缺失率以及不同样本数情况下的重构能力, 文中考察了缺失率固定为0.2, 0.5和0.7, 而样本数分别取40, 80和120的情况, 以及样本数固定为40, 80和120, 而缺失率分别取0.2, 0.5和0.7情况下的重构误差随所用POD模态阶数的变化, 如图 8所示.可以看出, 随着样本缺失率的增加, 不同样本数下的重构误差随POD模态阶数变化的收敛速度随之降低, 且能够达到的收敛精度也随之降低.当缺失率较低时, 不同样本数下的重构精度相差不大; 当缺失率较大时, 增加样本数可以提高重构精度.
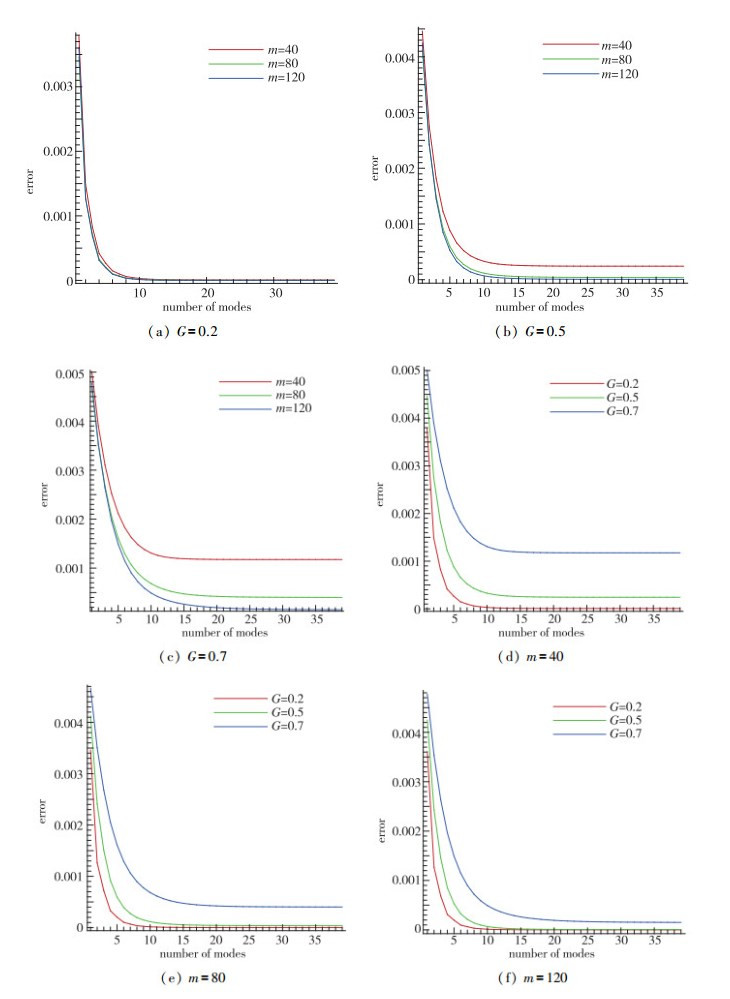
|
| 图 8 不同缺失率不同样本数的误差随重构所用POD模态阶数的变化曲线 Fig.8 Error versus number of modes for different gappiness and different snapshots |
图 9给出的是缺失率为0.7时, 分别选取样本数为40, 80和120, 缺失流场的填补结果与CFD的计算结果对比图, 图中所示结果的计算误差均已收敛.可以看出, 当缺失率为0.7时, 只选取40张样本得到的重构流场较为模糊, 而当样本数增加到80或者120时, 重构流场的清晰度明显提高, 且与CFD结果的吻合度较高.
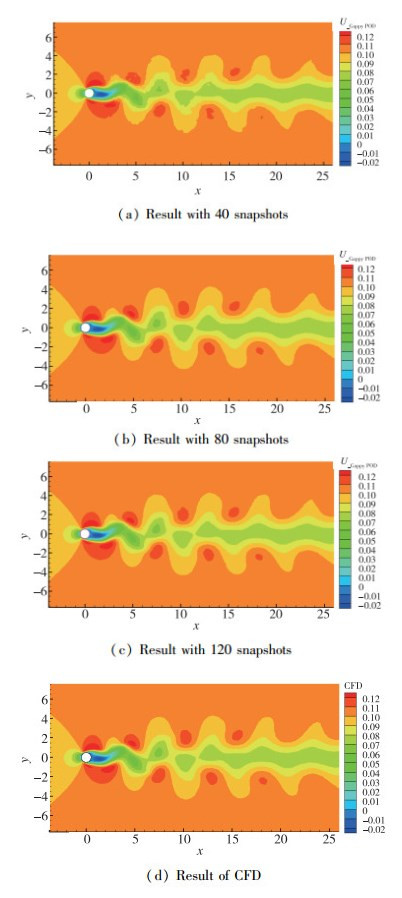
|
| 图 9 缺失率为0.7的Gappy POD填补结果与CFD计算结果对比 Fig.9 Comparison of reconstruction data from Gappy POD at a Gappy rate of 0.7 and original data from CFD |
本节对适用于缺失流场重构的Gappy POD方法和适用于不完整样本集的Gappy POD方法进行了研究, 以Re=100的二维圆柱绕流作为研究算例, 对上述两种方法的可行性进行了探究.得出如下结论:
(1) 对于已知一组POD模态, 只有某一流场存在部分数据缺失的情况, 适用于缺失流场重构的Gappy POD方法可以高效再现完整流场数据.随着重构所用POD模态阶数的增加, 重构误差快速收敛, 并且收敛于较高的重构精度.
(2) 对于用于求解POD模态的样本集各快照均存在部分数据缺失的情况, 适用于不完整样本集的Gappy POD方法可以高效再现整个样本集数据.随着重构所用POD模态阶数的增加, 重构误差快速收敛, 并且收敛于较高的重构精度.
(3) 对于用于求解POD模态的样本集各快照均存在部分数据缺失的情况, 当数据缺失率较低时, 使用较少的样本数即可达到较高的重构精度; 当数据缺失率较高时, 使用的样本数较低会导致重构精度不高, 可增加样本数以提高重构精度.
| [1] |
张来平, 邓小刚, 何磊, 等. E级计算给CFD带来的机遇与挑战[J]. 空气动力学学报, 2016, 34(4): 405-417. Zhang L P, Deng X G, He L, et al. The opportunity and grand challenges in computational fluid dynamics by exascale computing[J]. Acta Aerodynamica Sinica, 2016, 34(4): 405-417. DOI:10.7638/kqdlxxb-2014.0118 (in Chinese) |
| [2] |
张涵信. 关于CFD高精度保真的数值模拟研究[J]. 空气动力学学报, 2016, 34(1): 1-4. Zhang H X. Investigations on fidelity of high order accurate numerical simulation for computational fluid dyna-mics[J]. Acta Aerodynamica Sinica, 2016, 34(1): 1-4. (in Chinese) |
| [3] |
Moin P, Moser R D. Characteristic-eddy decomposition of turbulence in a channel[J]. Journal of Fluid Mechanics, 1989, 200: 471-509. DOI:10.1017/S0022112089000741 |
| [4] |
Zhao Y J, Zhao M, Li X J, et al. A modified proper orthogonal decomposition method for flow dynamic analy-sis[J]. Computers & Fluids, 2019, 182: 28-36. |
| [5] |
Jun S, Park K H, Kang H M, et al. Reduced order model of three-dimensional Euler equations using proper orthogonal decomposition basis[J]. Journal of Mechanical Science and Technology, 2010, 24(2): 601-608. DOI:10.1007/s12206-010-0106-0 |
| [6] |
陈鑫, 刘莉, 岳振江. 基于本征正交分解和代理模型的高超声速气动热模型降阶研究[J]. 航空学报, 2015, 36(2): 462-472. Chen X, Liu L, Yue Z J. Reduced order aerothermodynamoic modeling research for hypersonic vehicles based on proper orthogonal decomposition and surrogate method[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 462-472. (in Chinese) |
| [7] |
Yang J, Lu D, Deng Z, et al. A reduced-order extrapolation model based on proper orthogonal decomposition technique for Rayleigh-Bénard convection[J]. Journal of Physics:Conference Series, 2019, 1176(2): 022030. |
| [8] |
Lawrence S. Turbulence and the dynamics of coherent structures. Ⅰ. Coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. DOI:10.1090/qam/910462 |
| [9] |
Berkooz G, Holmes P, Lumley J L. The proper orthogonal decomposition in the analysis of turbulent flows[J]. Annual Review of Fluid Mechanics, 1993, 25(1): 539-575. DOI:10.1146/annurev.fl.25.010193.002543 |
| [10] |
Lumley J L. The structure of inhomogeneous turbulent flows[J]. Atmospheric Turbulence and Wave Propaga-tion, 1967, 166-178. |
| [11] |
魏斌斌, 高永卫, 邓磊, 等. 基于POD方法的高超声速边界层转捩判定方法[J]. 气体物理, 2016, 1(3): 25-30. Wei B B, Gao Y W, Deng L, et al. Transition method in hypersonic boundary later based on POD method[J]. Pysics of Gases, 2016, 1(3): 25-30. (in Chinese) |
| [12] |
李卓越, 白宏磊, 高南. 基于POD的受激励后向台阶分离流低阶模型[J]. 气体物理, 2017, 2(3): 33-43. Li Z Y, Bai H L, Gao N. Reduced order models of forced flow over a backward facing step based on POD method[J]. Physics of Gases, 2017, 2(3): 33-43. (in Chinese) |
| [13] |
Deane A E, Kevrekidis I G, Karniadakis G E, et al. Low-dimensional models for complex geometry flows:application to grooved channels and circular cylinders[J]. Physics of Fluids A:Fluid Dynamics, 1991, 3(10): 2337-2354. DOI:10.1063/1.857881 |
| [14] |
陈刚, 李跃明, 闫桂荣, 等. 基于POD降阶模型的气动弹性快速预测方法研究[J]. 宇航学报, 2009, 30(5): 1765-1769, 1796. Chen G, Li Y M, Yan G R, et al. A fast aeroelastic response prediction method based on proper orthogonal decomposition reduced order model[J]. Journal of Astronautics, 2009, 30(5): 1765-1769, 1796. DOI:10.3873/j.issn.1000-1328.2009.05.004 (in Chinese) |
| [15] |
姚伟刚, 徐敏, 叶茂. 基于特征正交分解的非定常气动力建模技术[J]. 力学学报, 2010, 42(4): 637-644. Yao W G, Xu M, Ye M. Unsteady aerodynamic force modeling via proper orthogonal decomposition ROM[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 637-644. (in Chinese) |
| [16] |
Xie D, Xu M, Dai H H, et al. Proper orthogonal decomposition method for analysis of nonlinear panel flutter with thermal effects in supersonic flow[J]. Journal of Sound and Vibration, 2015, 337: 263-283. DOI:10.1016/j.jsv.2014.10.038 |
| [17] |
谢丹, 徐敏. 基于特征正交分解的壁板热颤振分析[J]. 强度与环境, 2017, 44(2): 25-31. Xie D, Xu M. Thermal flutter analysis based on proper orthogonal decomposition method[J]. Structure and Environment Engineering, 2017, 44(2): 25-31. (in Chinese) |
| [18] |
Lucia D J, Beran P S, King P I. Reduced-order modeling of an elastic panel in transonic flow[J]. Journal of Aircraft, 2003, 40(2): 338-347. DOI:10.2514/2.3098 |
| [19] |
Dowell E H, Thomas J P, Hall K C. Transonic limit cycle oscillation analysis using reduced order aerodynamic models[J]. Journal of Fluids and Structures, 2004, 19(1): 17-27. DOI:10.1016/j.jfluidstructs.2003.07.018 |
| [20] |
陈刚, 李跃明, 闫桂荣, 等. 基于降阶模型的气动弹性主动控制律设计[J]. 航空学报, 2010, 31(1): 12-18. Chen G, Li Y M, Yan G R, et al. Design of active contrl law for aeroelastic systems via reduced order models[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(1): 12-18. (in Chinese) |
| [21] |
Chen G, Li Y M, Hu P. Design of active control law for aeroelastic system based on proper orthogonal decomposition reduced order model[R]. AIAA 2010-2624, 2010.
|
| [22] |
Iuliano E, Quagliarella D. Proper orthogonal decomposition, surrogate modelling and evolutionary optimization in aerodynamic design[J]. Computers & Fluids, 2013, 84: 327-350. |
| [23] |
Zhang Y D, Huang J T, Gao Z H, et al. Inverse design of low boom configurations using proper orthogonal decomposition and augmented Burgers equation[J]. Chinese Journal of Aeronautics, 2019, 32(6): 1380-1389. DOI:10.1016/j.cja.2019.03.017 |
| [24] |
Wang J C, Fu X, Huang G P, et al. Application of the proper orthogonal decomposition method in analyzing active separation control with periodic vibration wall[J]. International Journal of Turbo & Jet-Engines, 2019, 36(2): 175-184. |
| [25] |
Everson R, Sirovich L. Karhunen-Loève procedure for Gappy data[J]. JOSA A, 1995, 12(8): 1657-1664. DOI:10.1364/JOSAA.12.001657 |
| [26] |
方成, 周建华, 王孝利. 基于Gappy POD的S形扩压器稳态出口流场预测方法研究[J]. 科学技术与工程, 2017, 17(9): 84-90. Fang C, Zhou J H, Wang X L. Prediction method research of steady flow flied for S-shaped diffuser based on Gappy POD[J]. Science Technology and Engineering, 2017, 17(9): 84-90. DOI:10.3969/j.issn.1671-1815.2017.09.014 (in Chinese) |
| [27] |
段焰辉, 蔡晋生. 基于Gappy POD方法的翼型流场分析[J]. 航空工程进展, 2010, 1(1): 40-44. Duan Y H, Cai J S. Airfoil flow analysis based on Gappy POD method[J]. Advances in Aeronautical Science and Engineering, 2010, 1(1): 40-44. DOI:10.3969/j.issn.1674-8190.2010.01.010 (in Chinese) |
| [28] |
白俊强, 邱亚松, 华俊. 改进型Gappy POD翼型反设计方法[J]. 航空学报, 2013, 34(4): 762-771. Bai J Q, Qiu Y S, Hua J. Improved airfoil inverse design method based on Gappy POD[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4): 762-771. (in Chinese) |
| [29] |
罗佳奇, 唐肖, 孙海笑, 等. 基于Gappy POD的二维叶片压力反设计[J]. 工程热物理学报, 2016, 37(2): 268-271. Luo J Q, Tang X, Sun H X, et al. Inverse design of two-dimensional turbine blades by using Gappy POD[J]. Journal of Engineering Thermophysics, 2016, 37(2): 268-271. (in Chinese) |
| [30] |
Gunes H, Sirisup S, Karniadakis G E. Gappy data:To Krig or not to Krig?[J]. Journal of Computational Physics, 2006, 212(1): 358-382. |
| [31] |
Venturi D, Karniadakis G E. Gappy data and reconstruction procedures for flow past a cylinder[J]. Journal of Fluid Mechanics, 2004, 519: 315-336. DOI:10.1017/S0022112004001338 |
| [32] |
Braza M, Chassaing P, Minh H H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder[J]. Journal of Fluid Mechanics, 1986, 165: 79-130. DOI:10.1017/S0022112086003014 |
| [33] |
Mittal S. Effect of a "slip" splitter plate on vortex shedding from a cylinder[J]. Physics of Fluids, 2003, 15(3): 817-820. DOI:10.1063/1.1540632 |
| [34] |
Tritton D J. Experiments on the flow past a circular cylinder at low Reynolds numbers[J]. Journal of Fluid Mechanics, 1959, 6(4): 547-567. DOI:10.1017/S0022112059000829 |



