气动弹性问题一直是飞行器设计中备受关注的重要问题, 在未来的飞行器设计中仍将占有重要地位.现代飞行器设计日益追求高速度、高机动性, 使得飞行器越来越呈现出轻结构和大柔性等特点, 气动弹性问题也日渐突出[1].随着高速飞行器研究工作的逐渐深入, 飞行器的性能不断提升, 高速飞行器的结构重量占比需要大幅降低, 对结构设计人员将面临巨大的压力和挑战.结构设计的余量越来越小, 结构越来越“纤细”, 导致结构的柔性相对增大, 飞行器的气动弹性影响日益突出.此外, 与传统飞行器相比, 高速飞行器经受的热力学环境更为严酷, 高速飞行带来的高温高压引起结构变形, 严重地改变了气动载荷的分布, 长时间的气动加热使结构弹性模量减小, 导致结构刚度下降, 进一步使结构变形增大, 这种气动力/热/结构互相耦合的现象形成了高速飞行器热气动弹性问题.因此, 高速飞行器的气动弹性问题自航天飞行器出现以来, 就成为一项重要的科学问题.
随着计算机的快速发展, 通过CFD手段求解N-S方程用于预测气动力和气动热被认为具有可靠的精度, 耦合非稳态传热以及结构有限元分析技术逐步成熟, 研究内容也很丰富, 但由于热气弹问题的复杂性, 在研究中存在大量的、不同程度的近似情况[2-9].在早期研究中, Boit对考虑热应力情况下的双楔形机翼的静气弹稳定性进行了研究[2], 其热应力的引入采用了沿弦向抛物线分布的近似温度场.张伟伟等[5]采用了气动力工程算法对超声速/高超声速翼型进行了气动弹性计算, 虽未考虑热环境对结构的影响, 但结果表明采用工程方法进行的气动弹性计算还是满足要求的.张伟伟等对高超声速热气动弹性问题进行了研究, 对升温模型的振动特性和临界速度进行了分析, 但其温度场采用均匀温升假设, 与真实情况存在一定区别[7].刘磊等在真实热环境与热结构情况下, 采用气动力/气动热/热结构耦合的方法对简单翼面结构静态热气动弹性特性进行了研究, 表明气动加热对机翼模型的气动特性影响显著[8].此外, 研究表明获得准确的热气弹静变形量对飞行器结构颤振分析也十分重要[10].
本文采用气动力/气动热/结构耦合的方法对高速细长体飞行器模型热静气弹问题进行了研究.对该飞行器高速飞行状态进行了热静气动弹性特性计算, 并与不考虑热环境影响情况下的计算结果进行了对比分析.
1 计算流程静气动弹性计算中, 在气动力作用下, 结构的平衡方程可写作
| $ \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{F}} $ | (1) |
其中, K为结构刚度矩阵, u为结构自由度位移矢量, F为气动载荷矢量.
对于线弹性结构力学问题, K为常量(是基于线弹性假设)[11], 已知气动力F则可以求出结构变形u.依据初始构型获得的气动力, 根据公式(1)可以计算出相应的结构变形, 结构形状改变影响原有的气动外形, 从而又使气动力发生改变, 即气动力F随着结构外形u的改变而变化.由结构变形引起的气动力变化须通过重新进行流场计算才能获得, 所以要求解结构的真实变形, 须采用循环迭代方法求解.
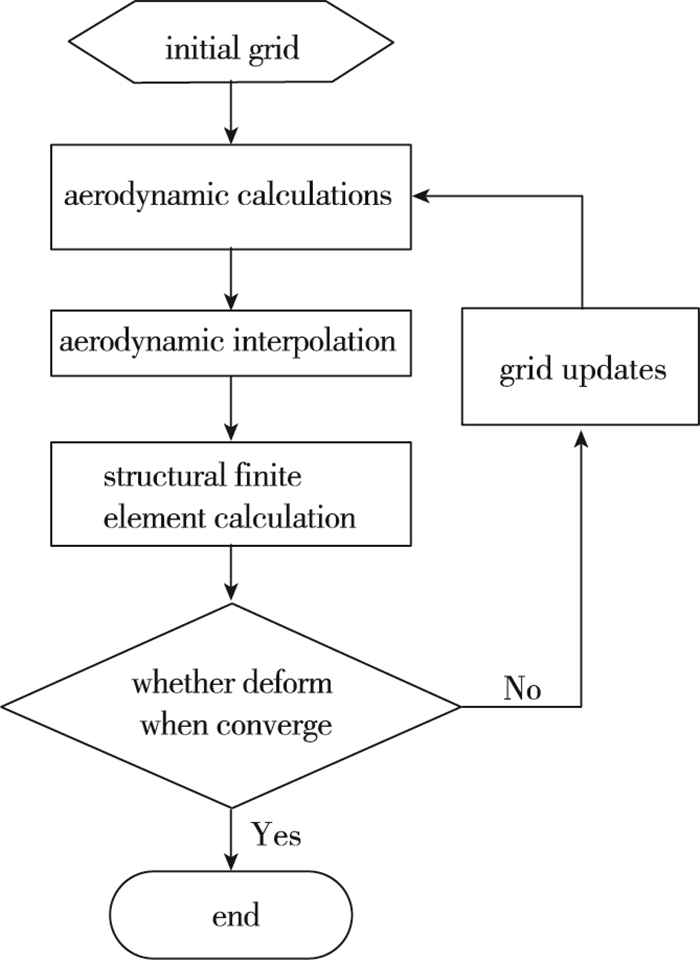
对气动弹性计算, 在每一轮迭代计算中, 气动力计算求解器使用新的外形流场网格, 此网格由上一轮迭代的结构变形获得, 从而求解出新的气动力载荷.再通过结构有限元求解器得出结构对于气动力的响应.迭代过程直到飞行器结构变形收敛为止. 图 1即为静气动弹性计算流程框图.
|
| 图 1 静气动弹性计算流程图 Fig.1 Flow chart of the static aeroelastic calculation |
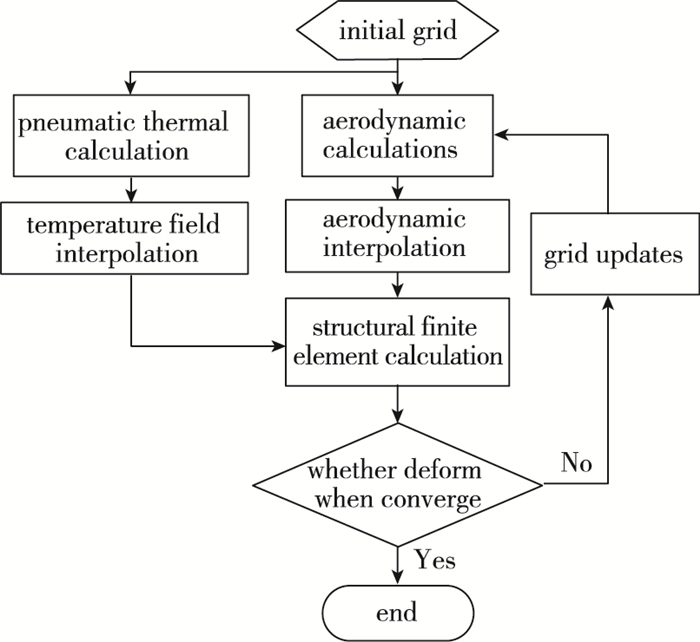
热气动弹性问题是一个多学科问题, 一次性完全求解这样的多学科耦合问题非常复杂, 目前难以在工程上实现.如果基于前述提及的在分析热气动弹性问题中仅考虑气动加热对结构弹性力部分影响的假设, 则其分析过程就得以简化.通过这一简化, 我们可以得到求解静态热气动弹性问题的最终计算流程, 如图 2所示.
|
| 图 2 热静气动弹性计算流程图 Fig.2 Flow chart of the thermostatic aeroelastic calculation |
这一计算流程与传统的静气动弹性计算流程的区别就在于结构有限元计算中加入了温度场对结构热变形的影响.在变形量相对较小的情况下, 可以忽略结构变形对热环境造成的影响.
2 计算方法 2.1 气动力/热计算控制方程本文气动力和热流通过求解Reynolds平均N-S方程, 守恒形式[12]为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0\\ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}\\ \frac{{\partial e}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {{u_j}e} \right) = \frac{\partial }{{\partial {x_j}}}( - {u_j}p + {u_i}{\tau _{ij}} + {q_i}) \end{array} $ | (2) |
式中,
各参数的意义详见文献[13].为了使式(2)封闭, 需要对式(2)中的Reynolds应力做出各种假设.从对模式处理的出发点不同, 一般可将湍流模式分为Reynolds应力模型和涡黏性模型两类.受计算条件的约束, Reynolds应力模型计算量巨大, 使其应用范围受到限制, 在工程湍流问题中广泛应用的是涡黏性模型[12].
壁面热流由下式计算
| $ {q_{\rm{w}}} = \frac{{M{a_\infty }}}{{R{e_\infty }}}\frac{\mu }{{(\gamma - 1)\mathit{Pr}}}\frac{{\partial T}}{{\partial \mathit{\boldsymbol{n}}}} $ | (3) |
其中, Ma∞和Re∞分别为来流Mach数和Reynolds数, μ为气体动力黏性系数, Prandtl数Pr为0.72, 比热比γ=1.4, n为壁面法向.
2.2 CFD数值离散方法采用有限体积法求解Reynolds平均可压缩N-S方程和模型输运方程; 无黏通量采用Roe的通量差分分裂(flux-difference splitting, FDS)格式, 并通过限制器[14]来抑制振荡; 黏性通量采用2阶中心差分格式; 时间推进采用LU-SGS隐式方法.
2.3 热应力与变形计算方法对结构热应力场/位移场的计算是通过热弹性力学控制方程组完成的.该方程组由弹性力学的变分原理很容易化为经典的有限元求解方程
| $ \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{a}} = \mathit{\boldsymbol{P}} $ | (4) |
其中, K是已知的结构整体刚度矩阵, P是已知的结点位移列阵.对物体受热产生的应力问题, 物体由于热膨胀结构点载荷列阵, 它们是由单元刚度矩阵和单元等效结点载荷列阵集合而成. a则是待求解的结构节点列阵.
对于物体受热产生的应力问题, 结构由于热膨胀只产生线应变, 而剪切应变为零.这种由于热变形产生的应变可以看作初应变ε0.
| $ {\varepsilon _0} = \alpha (\phi - {\phi _0}) $ | (5) |
在这种情况下应力应变关系就可表示成
| $ \sigma = D(\varepsilon - {\varepsilon _0}) $ | (6) |
其中, α是材料的热膨胀系数(1/℃), 对各向同性材料来说, 各方向的膨胀系数α通常是相同的; ϕ0是结构的初始温度场; ϕ是结构的稳态或瞬态温度场. ϕ可由温度场分析得到的单元结点温度插值求得.
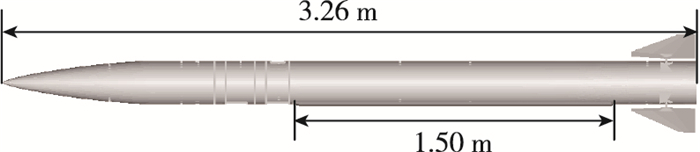
3 计算模型 3.1 细长体飞行器模型假设某简单细长体飞行器长度为3 260 mm, 飞行器下端采用腹鳍保护电缆线长度为1 500 mm; 4片操纵面采用"X"布局方案.头部结构材料选用铸钢, 腹鳍和飞行器主体选用合金钢, 舵面采用不锈钢.飞行器模型外形示意图见图 3.
|
| 图 3 飞行器模型外形示意图 Fig.3 Schematic diagram of the aircraft model |
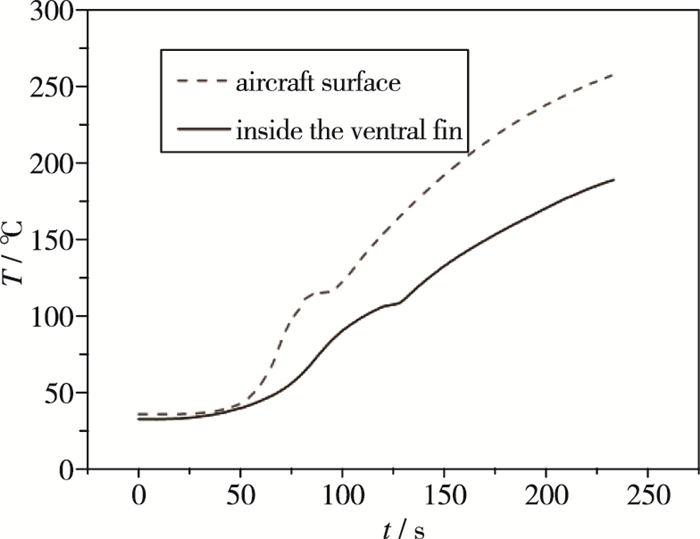
通过CFD手段计算飞行器Ma=3.5, 攻角4°状态的表面热流, 通过结构真实热传递形式计算飞行器各部件温度随时间变化曲线.由于飞行器各部件采用材料和结构传热形式不同, 飞行器不同部位温度变化不同, 产生温度梯度, 飞行器表面温度曲线见图 4.
|
| 图 4 飞行器部件温度随时间变化曲线 Fig.4 Aircraft component temperature versus time curves |
根据飞行器模型主要承力结构的几何模型、所用材料及材料属性, 设计飞行器模型并建立静气动弹性分析的结构有限元模型, 所建模型包括主要的承力和传力结构件, 且保证整体及部件的结构质量和刚度特性合理、真实. 表 1给出了飞行器模型的配重和不配重后的模态试验结果和结构有限元模型计算结果的对比.
| 下载CSV 表 1 模态试验与有限元模型计算一弯频率对比 Tab.1 Comparison of modal test and finite element model for calculating bending frequency |
对比设计模型的模态试验值和结构有限元模型的计算值, 发现一致性良好, 说明有限元模型可准确模拟飞行器结构刚度特性, 且精度较高.
4.2 热考核试验验证为验证有限元模型预测热变形精度, 对飞行器主体结构进行热环境考核刚度试验, 图 5给出了飞行器主体和对应的主体有限元模型.

|
| 图 5 试验件和有限元模型 Fig.5 Test piece and finite element model |
试验过程中飞行器主体一端固支为悬臂梁形式, 采用石英灯对有腹鳍段位置加热, 测量自由端各向位移.
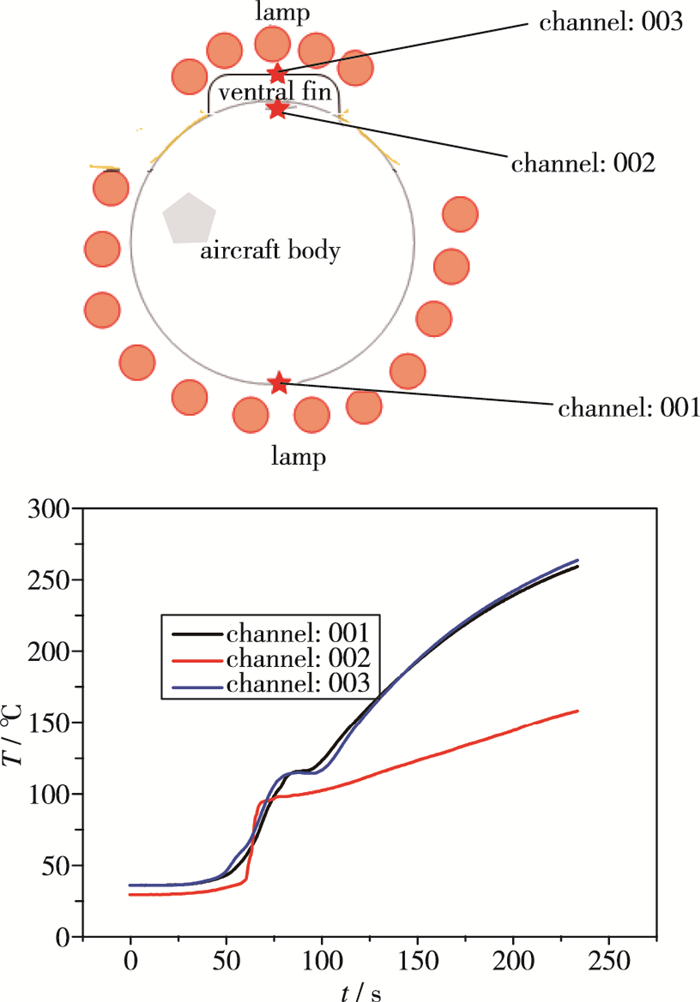
试验中采用3个通道测量飞行器主体温度变化曲线, 通道_001为加热段飞行器主体外壁温度, 通道_002为腹鳍覆盖飞行器主体壁面温度, 通道_003为腹鳍外壁温度, 见图 6.试验通过石英灯加热, 发现由于结构和传热形式的原因飞行器被腹鳍覆盖内外壁面温度存在差异, 与上述热环境计算结果一致.
|
| 图 6 试验测点和温度曲线 Fig.6 Test points and temperature curves |
对有限元模型施加试验中230 s时刻温度载荷, 热变形计算值和试验结果见图 7.

|
| 图 7 计算值和试验结果 Fig.7 Calculated values and test results |
试验(230 s)时刻, 飞行器主体壳体自由端伸长6 mm, 向上位移为15 mm, 腹鳍也有明显上翘的痕迹.对有限元模型施加230 s时刻的温度场, 热变形计算结果为自由端轴向位移6.8 mm, 垂直轴向位移为16.2 mm.表明采用有限元模型在热变形预测方面具有良好精度.
计算和试验值出现垂直于轴向位移, 主要由于飞行器腹鳍覆盖内外温差所致.
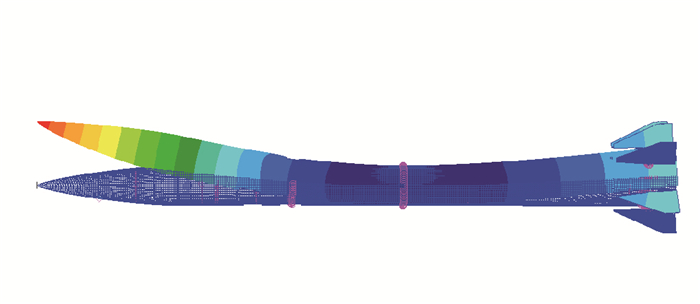
4.3 静气弹变形结果对飞行器进行气动力/结构耦合静气弹分析, 计算状态为Ma=3.5, H=3 km.将气动力插值到结构有限模型中, 耦合迭代到达结构变形位移收敛.如图 8所示, 在正攻角4°状态, 飞行器受到向上的气动力, 在气动力作用下头部和尾部都有升力方向位移, 头部向上位移为10.8 mm, 尾部向上位移为6.62 mm.
|
| 图 8 静气弹计算位移图(20倍放大) Fig.8 Displacement from static aeroelastic calculation(20 times magnification) |
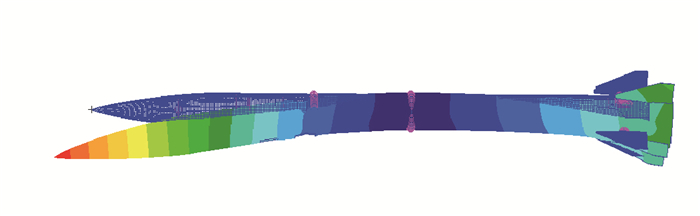
同样对该状态采用力/热/结构耦合分析方法, 首先将温度场插值到结构有限元模型中, 认为温度场在耦合迭代中保持不变.耦合迭代气动力和结构位移达到收敛.如图 9所示, 该状态对结构同时施加气动力和温度载荷, 飞行器呈现出与只有力加载相反的变形规律, 其中头部向下位移为17.6 mm, 尾部向下位移为8.6 mm.
|
| 图 9 热气弹计算位移图(20倍放大) Fig.9 Displacement from thermostatic aeroelastic calculation(20 times magnification) |
头部和尾部出现向下位移主要因是:飞行过程中腹鳍覆盖的飞行器主体没有空气摩擦直接加热, 主要通过热传导使温度升高, 温度上升较慢; 而未被腹鳍覆盖的飞行器主体结构直接由空气对其加热, 温度上升较快, 飞行器被腹鳍覆盖内外温差最大可达到200 ℃.腹鳍位于飞行器腹部, 飞行器下表面温度比上表面温度低, 使下表面膨胀程度比上表面小, 使头部和尾部产生向下位移.飞行器虽然受到向上的气动力作用, 但气动力产生向上的弹性变形不足以抵消热应力变形, 致使飞行器头部和尾部产生热应力主导的向下的位移.
4.4 气动特性变化分别对变形前后的飞行器气动特性进行分析, 气动特性包括(升力、阻力和俯仰力矩特性), 表 2和3给出了未考虑热应力和考虑热应力变形后飞行器气动特性变化量.
| 下载CSV 表 2 变形前后力系数对比 Tab.2 Comparison of force coefficient before and after deformation |
| 下载CSV 表 3 变形前后力矩系数对比 Tab.3 Comparison of moment coefficient before and after deformation |
由于变形规律相反使变形前后气动特性规律不同.只有力载荷时变形使飞行器升力减小而阻力基本不变, 飞行器升阻比降低, 压心前移, 主要由于飞行器尾部有操纵面, 后半段提供飞行器60%以上的升力, 飞行器尾部产生向上位移使其等效攻角降低, 升力减小.同理, 在力/热/结构耦合分析时, 飞行器尾部有向下位移, 增大了飞行器后半段等效攻角, 使其升力增加, 这就有飞行器升力、阻力增加和压心后移的结论.
5 结论采用气动力/热/结构耦合的方法对简单细长体飞行器热气动弹性特性进行分析, 并且通过热考核试验验证热应力变形计算的准确度, 有如下结论:
(1) 对结构有限元模型施加温度载荷可准确预测结构热应力变形;
(2) 在有气动加热的情况下, 综合考虑受力和温度梯度对结构变形的影响, 可得到更为真实的结构变形和气动弹性修正量.
本文力/结构耦合和力/热/结构耦合计算得到变形和气动特性影响规律相反, 虽然只适用于本文分析状态, 但可以肯定一点, 气动加热对气动弹性特性影响显著.因此, 准确预测结构气动加热特性才能获得高速飞行器真实的气动弹性修正量.
| [1] |
杨超, 许赟, 谢长川. 高超声速飞行器气动弹性力学研究综述[J]. 航空学报, 2010, 31(1): 1-11. Yang C, Xu Y, Xie C C. Review of the study of aerodynamic elastic mechanics of hypersonic aircraft[J]. Journal of Aeronautical Science, 2010, 31(1): 1-11. (in Chinese) |
| [2] |
Biot M A. Influence of thermal stresses on the aeroelastic stability of supersonic wings[J]. Journal of the Aeronautical Sciences, 1957, 24(6): 418-420. DOI:10.2514/8.3871 |
| [3] |
Ericsson L E, Almroth B O, Bailie J A. Hypersonic aerothermoelastic characteristics of a finned missile[R]. AIAA 1979-231, 1979.
|
| [4] |
Rodgers J. Aerothermoelastic analysis of a NASP-like vertical fin[R]. AIAA 1992-2400-CP, 1992.
|
| [5] |
张伟伟, 樊则文, 叶正寅, 等. 超音速、高超音速机翼的气动弹性计算方法[J]. 西北工业大学学报, 2003, 21(6): 687-691. Zhang W W, Fan Z W, Ye Z Y, et al. The calculation method of aerodynamic elasticity of supersonic and hypersonic wings[J]. Journal of Northwestern Polytechnical University, 2003, 21(6): 687-691. DOI:10.3969/j.issn.1000-2758.2003.06.012 (in Chinese) |
| [6] |
Thornton E A, Dechaumphai P. Coupled flow, thermal, and structural analysis of aerodynamically heated panels[J]. Journal of Aircraft, 1988, 25(11): 1052-1058. DOI:10.2514/3.45702 |
| [7] |
张伟伟, 夏巍, 叶正寅. 一种高超音速热气动弹性数值研究方法[J]. 工程力学, 2006, 23(2): 41-46. Zhang W W, Xia W, Ye Z Y. A numerical method for the study of hypersonic thermal aerodynamic elasticity[J]. Engineering Mechanics, 2006, 23(2): 41-46. DOI:10.3969/j.issn.1000-4750.2006.02.007 (in Chinese) |
| [8] |
刘磊, 桂业伟, 耿湘人, 等. 高超声速飞行器热气弹静态问题研究[J]. 空气动力学学报, 2013, 31(5): 559-563. Liu L, Gui Y W, Geng X R, et al. Study on the thermal aeroelastic static issues in hypersonic aircraft[J]. Acta Aerodynamica Sinica, 2013, 31(5): 559-563. (in Chinese) |
| [9] |
窦怡彬, 徐敏, 安效民, 等. 高超声速舵面颤振分析[J]. 工程力学, 2009, 26(11): 232-237. Dou Y B, Xu M, An X M, et al. Hypersonic rudder-surface vibration analysis[J]. Engineering Mechanics, 2009, 26(11): 232-237. (in Chinese) |
| [10] |
张伟伟.基于CFD技术的高效气动弹性分析方法研究[D].西安: 西北工业大学, 2006. Zhang W W. The high-efficiency aerodynamic elastic analysis method based on CFD technology[D]. Xi'an: Journal of Northwestern Polytechnical University, 2006(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10699-2007214276.htm |
| [11] |
黄志澄. 高超声速飞行器空气动力学[M]. 北京: 国防工业出版社, 1995: 17-22. Huang Z C. Aerodynamics of hypersonic flight vehicle[M]. Beijing: National Defense Industry Press, 1995: 17-22. (in Chinese) |
| [12] |
Wilcox D C. Turbulence modeling for CFD[M]. 3rd ed. California: DCW Industries Inc, 2006: 243-249.
|
| [13] |
阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 221-223. Yan C. Methods and applications of computational fluid mechanics[M]. Beijing: Beihang University Press, 2006: 221-223. (in Chinese) |
| [14] |
Van Leer B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov's method[J]. Journal of Computational Physics, 1979, 32(1): 101-136. |



