2. 西安交通大学机械工程学院, 陕西西安 710049
2. School of Mechanical Engineering, Xi'an Jiaotong Univeristy, Xi'an 710049, China
大气压低温等离子体由于能够可控、节能、高效地产生活性粒子, 近年来越来越受到工业和科学界重视. 从臭氧产生、聚合物处理、激光制造、污染控制、生物除菌、医药治疗, 到流动控制、点火助燃、薄膜工艺, 低温等离子体的应用领域正在迅速扩展[1-8].
在大气压下, 产生等离子体的基本方法之一是在由金属制造的针板结构的气隙间施加高电压. 高电压在针尖形成局部强电场, 驱动电子加速并引发雪崩-流注放电, 形成一条细长的放电通道, 并在数十个纳秒内击穿整个气隙[9-10].
数值计算是测试理论假设、验证实验结论和预测放电参数与行为的有力工具. 雪崩-流注放电是一个多尺度系统, 包含了诸多过程, 包括化学反应、组分输运、电磁场传播以及流体耦合等, 高精度、高效率地模拟这个系统是一个巨大的挑战.
首先, 流注的动力学过程是高度非线性的. 由于在流注头部以及与介质间隙, 电场与空间电荷分离层直接耦合, 对应区域的计算需要极高的空间精度. 另外, 电荷分离层通常具有弧度, 因而纯一维模型不足以准确描述流注的传播. 文献[11]使用了1.5维模型, 通过将二维Poisson方程和一维输运方程结合实现了径向方向流注的模拟, 但是该方法无法模拟负流注和表面流注. 文献[12-13]引入了SG方法模拟二维轴对称几何下的火花和辉光放电. 文献[14-15]分析了正流注和负流注的动力学过程. SG方法经文献[16-17]的改良, 用于精确模拟针-板放电. 文献[18]进一步对算法进行改良, 用于计算流注与介质接触问题. 其次, 流注传播是一个多空间尺度问题. 大气压下, 流注头部的电荷分离层厚度仅为几十个电子自由程大小(几十微米). 与此同时, 流注的传播距离却可达数厘米. 因此, 流注模型须解析跨越了4个量级的两种空间尺度. 最常用的解决方案是使用非均匀网格, 并在等离子体区域加密. 文献[19-20]等采用了最新的结构化自适应网格, 使得计算效率得到了显著提高. 流注也是一个多时间尺度问题. 流注的传播时间一般为几十到数百纳秒, 而大气压下捕捉流注输运过程所需的最小时间尺度为10-14 s, 跨越了7~8个数量级. 文献[21-23]使用了半隐式推进, 文献[24]使用异步时间推进的方法克服了这些困难. 再次, 流注具有强非局域特性, 使得并行加速变得十分困难. 这种非局域性主要是由于电场和光电离的全局特性. 在有介质的情况下, 边界特性的变化会导致局部电场的陡增和间断. 为了克服非局域性问题, 一种解决方案是使用局域能量近似, 将化学反应速率和输运特性表达为局域平均电子能量的函数. 另一种方法是引入对电离反应速率系数的修正项. 更加直接的方法是采用混合模拟, 考虑快速电子(逃逸电子)的形成. 文献[25]将粒子模型用于模拟流注头部, 将流体模型用于模拟流注主体. 这种“电子束-主体区”方法综合了电子Monte Carlo模型和流体模型, 得到了大量研究[26-28]. 在一些专注于逃逸电子、流注分叉现象的研究工作中, 纯粒子-Monte Carlo模拟也得到了应用[29-32].
近年来, 很多课题组采用商用有限元软件COMSOL Multiphysics开展流注模拟. 其在模拟等离子体放电中有一些独特的优势: (1)具有友善的用户界面, 便于快速入门并获得一些初始结果; (2)有限元方法使其可以适应几乎任何复杂几何结构; (3)自带的等离子体模块能够大大减少编程工作量; (4)自适应网格特性使其能够在一定程度上克服有限元商用软件的通病——网格数量太小; (5)自带的后处理系统为计算结果分析提供了有力的工具; (6)拥有通用性的偏微分方程模块, 可以较为自由地组织模型.
尽管COMSOL Multiphysics具有以上优势, 但是也存在很多非常显著且难以解决的缺陷, 导致其无法作为研究在大气压下通常呈流注形态的纳秒脉冲放电的理想工具: (1)COMSOL Multiphysics的等离子体模块采用了标准Galerkin方法, 该方法无法捕捉输运占优的流注头部区域的强间断面, 导致计算结果严重失真, 呈伪扩散形体; (2)商用软件的“黑盒子”模式使得无法对程序运行模式进行任何修改, 因而在模拟遇到问题时只能凭借猜测处理, 几乎没有办法调试; (3)全隐式的数值格式使得时间积分对计算域任何一点扰动都十分敏感, 无关紧要处的一个奇异点就会导致整个模型计算效率下降, 收敛极其困难; (4)与基于质量守恒的有限体积法不同, 有限元方法本质是基于能量守恒原理的, 不具有保证质量守恒的特性, 在等离子体计算中不可避免会出现负浓度情况; (5)COMSOL Multiphysics直接求解大规模矩阵而不充分利用并行计算机结构, 使其存在计算速度缓慢、内存消耗巨大的问题.
本文介绍一种以弱形式偏微分方程形式在COMSOL Multiphysics软件中引入人工稳定项, 用以克服等离子体模拟中出现的数值振荡和伪扩散问题的解决方案. 文章分3个部分, 第1部分以弱形式的方式推导人工稳定项的输入形式, 第2部分给出基准验证和实验验证, 最后给出结论.
1 弱形式与人工稳定项分析引言所述的COMSOL Multiphysics缺陷, 发现缺陷(3)和(4)是当等离子体与介质、金属接触时存在的最主要问题, 而对于针-板型的体放电而言, 这些缺陷不会对计算结果产生太大影响. 缺陷(5)无法克服, 而缺陷(1)和(2)可以通过引入弱形式偏微分方程, 添加人工稳定项来解决. 本节将对在COMSOL中构建弱形式PDE引入流线扩散人工稳定性(streamline upwind Petrov Galerkin method, SUPG)进行阐述.
首先, 利用COMSOL Multiphysics建立一套最简单的等离子体方程体系: Poisson方程、Helmholtz方程和输运方程. 其中, Poisson方程和Helmholtz方程是单纯的椭圆形方程, 可以直接使用偏微分方程模块以“黑盒子”的形式求解. 输运方程则用弱形式偏微分方程表达.
在纳秒放电时间尺度下, 可以假设离子和中性粒子不运动, 仅求解不包含输运项的反应方程即可
| $ \frac{{\partial {n_{\rm{i}}}}}{{\partial t}} - \nabla \left( {{D_{\rm{i}}}\nabla {n_{\rm{i}}}} \right) = {S_{\rm{i}}} + {S_{{\rm{ph}}}} $ |
式中, ni为离子密度, Di为离子扩散率, Si为化学反应主导的离子产生率, Sph为光电离主导的离子产生率.
电子的输运方程为
| $ \frac{{\partial {n_{\rm{e}}}}}{{\partial t}} - \nabla \left( {{D_{\rm{e}}}\nabla {n_{\rm{e}}} + {\mu _{\rm{e}}}{n_{\rm{e}}}\nabla \varPhi } \right) = {S_{\rm{e}}} + {S_{{\rm{ph}}}} $ |
式中, ne为电子密度, De为电子扩散率, μe为电子迁移率, Φ为电势, Se为化学反应主导的电子产生率, Sph为光电离主导的电子产生率. 电子扩散率、迁移率和化学反应电子产生率均可通过开源电子能量分布函数计算软件BOLSIG+计算得到. 为了便于比对, 本文中的反应速率系数和输运系数均采用了文献[16]中给定的公式计算
| $ 0 = \nabla \left( {{D_{\rm{e}}}\nabla {n_{\rm{e}}} + {\mu _{\rm{e}}}{n_{\rm{e}}}\nabla \varPhi } \right) - \frac{{\partial {n_{\rm{e}}}}}{{\partial t}} + {S_{\rm{i}}} + {S_{{\rm{ph}}}} $ |
以上方程乘以“试函数”u(x, y, z), 并对有限单元进行体积分, 可以得到
| $ \begin{array}{*{20}{l}} {\iiint\limits_V {\left( {\nabla \cdot \left( {{D_{\rm{e}}}\nabla {n_{\rm{e}}}} \right)} \right)} u{\rm{d}}V + \iiint\limits_V {\left( {\nabla \cdot \left( {{n_{\rm{e}}}{\mu _{\rm{e}}}\nabla \varPhi } \right)} \right)} u{\rm{d}}V - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \iiint\limits_V {\left( {\frac{{\partial {n_{\rm{e}}}}}{{\partial t}}} \right)} u{\rm{d}}V + \iiint\limits_V {\left( {{S_{\rm{i}}} + {S_{{\rm{ph}}}}} \right)} u{\rm{d}}V = 0} \end{array} $ |
对上式前两项进行分部积分, 并简化可得
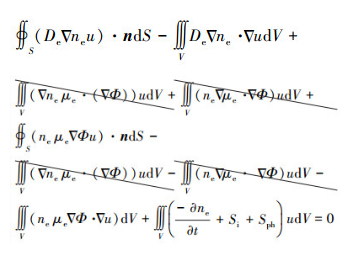
|
由此, 可以得到能够直接输入COMSOL Multiphysics的弱形式方程
| $ \begin{array}{*{20}{l}} { - \iiint\limits_V {{D_{\rm{e}}}} \nabla {n_{\rm{e}}} \cdot \nabla u{\rm{d}}V - \iiint\limits_V {\left( {{n_{\rm{e}}}{\mu _{\rm{e}}}\nabla \varPhi \cdot \nabla u} \right)} {\rm{d}}V + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \iiint\limits_V {\left( { - \frac{{\partial {n_{\rm{e}}}}}{{\partial t}} + {S_{\rm{i}}} + {S_{{\rm{ph}}}}} \right)} u{\rm{d}}V + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\nolimits_S {\left( {{D_{\rm{e}}}\nabla {n_{\rm{e}}}u} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}S} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\nolimits_S {\left( {{n_{\rm{e}}}{\mu _{\rm{e}}}\nabla {\varPhi _u}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}S} = 0} \end{array} $ | (1) |
式中, 第1行是等离子体计算域的弱形式偏微分方程, 第2行代表自然满足的边界条件. 式(1)可以写成更明晰的形式
| $ \begin{array}{*{20}{l}} {\iiint\limits_V {\left( {\left( { - {D_{\rm{e}}}\nabla {n_{\rm{e}}} - {n_{\rm{e}}}{\mu _{\rm{e}}}\nabla \varPhi } \right) \cdot \nabla u + \left( { - \frac{{\partial {n_{\rm{e}}}}}{{\partial t}} + {S_{\rm{i}}} + } \right.} \right.} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {{S_{{\rm{ph}}}}} \right)u} \right){\rm{d}}V + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\nolimits_S {\left( {{D_{\rm{e}}}\nabla {n_{\rm{e}}} + {n_{\rm{e}}}{\mu _{\rm{e}}}\nabla \varPhi } \right)u \cdot \mathit{\boldsymbol{n}}{\rm{d}}S} = 0} \end{array} $ |
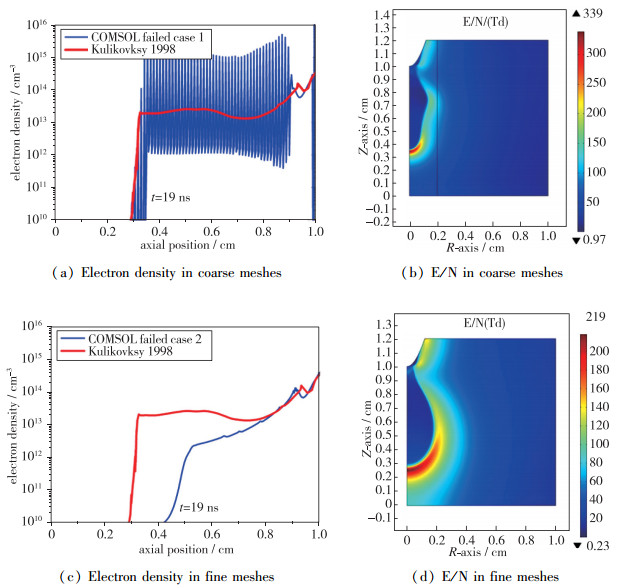
方程(1)所描述的漂移-扩散过程, 如果求解的区域被扩散过程主导, 那么传统的COMSOL标准Galerkin差分方法可以获得稳定可靠的解. 如果计算区域是漂移主导, 那么方程(1)则表现出双曲型方程特性, 传统的数值方法变得非常不稳定, 计算结果要么会在粗糙的网格下剧烈振荡, 要么在精细的网格下形成伪扩散解. 在前述方程的基础上, 利用COMSOL直接复现文献[16]中的轴对称针-板放电基准算例, 采用相同的方程(连续方程+Poisson方程), 分别使用50 μm和15 μm两种尺寸网格开展计算, 结果如图 1(a)~(d)所示.
|
| 图 1 使用COMSOL标准Galerkin格式计算针板放电并与Kulikovsky流注基准案例[16]对比结果 Fig.1 Results comparison between standard COMSOL model and Ref[16] |
图 1(a)和(c)对比了使用COMSOL Multiphysics在两种网格条件下计算的流注轴向电子密度分布(蓝线)和基准算例中的轴向流注通道电子密度(红线). 在粗网格下, COMSOL Multiphysics计算所得流注能够复现基准算例流注传播速度, 如图 1(b)所示, 但是整个放电通道内出现了图 1(a)中剧烈的非物理数值振荡, 计算结果无法分析理解. 如果仅仅加密网格, 如图 1(c)所示, 计算轴向电子密度不再产生数值振荡, 但是流注传播距离远远落后于基准算例, 图 1(d)表明, COMSOL Multiphysics标准有限元方法无法捕捉到基准算例中的电子雪崩-流注转捩, 计算结果呈扩散流注状. 这两个案例清楚地表明, 使用COMSOL Multiphysics默认的数值格式和计算方法不可能正确计算大气压流注. 本文使用COMSOL Multiphysics内置的等离子体模块进行测试, 也得到了同样的错误结果.
这种数值不稳定性, 源于计算网格与算法不匹配, 有限元中的标准Galerkin方法与有限体积/有限差分中的标准SG方法一样, 在高气压条件下, 计算等离子体流注的准确性会显著下降. 假设电子扩散系数符合Einstein关系, 那么为了保证计算结果的准确性, 须保证以下关系[17]
| $ \frac{{\left| {\Delta {E_k}} \right|{h_k}}}{{2{T_{{\rm{e}}k}}}} \ll 1 $ | (2) |
式中, k表示第k个网格节点, ΔE为电场强度梯度, h为网格尺寸, Te为电子温度. 上式表明, 两个相邻节点的电势差须远小于电子温度. 对于高气压情况, 若要满足该条件, 则需要极高的网格密度, 这使得高性能计算几乎不可能. 方程(2)所规定的严苛的网格条件在COMSOL下基本不可能实现(除非计算域非常小). 为此, 可以通过引入人工稳定性[33-37]提升计算精度. 最广泛使用的人工稳定性方法之一, 就是流线扩散稳定SUPG方法[33-34]. 通过弱形式方程, 在COMSOL Multiphysics中对各个有限单元添加人工稳定项
| $ \sum\limits_{e = 1}^{{n_{{\rm{el}}}}} {\int_{{\varOmega _{{\rm{el}}}}} P } \left( {{u_h}} \right){\tau ^e}R\left( {{n_{{\rm{eh}}}}} \right){\rm{d}}\Omega $ | (3) |
式中, 各项的含义如下
| $ {P\left( {{u_h}} \right) = {\mu _{\rm{e}}}\frac{{\partial \varPhi }}{{\partial x}}\frac{{\partial u}}{{\partial x}} + {\mu _{\rm{e}}}\frac{{\partial \varPhi }}{{\partial y}}\frac{{\partial u}}{{\partial y}}} $ |
| $ {{\tau ^{\rm{e}}} = \frac{1}{2}\left( {{\alpha _x}\frac{h}{{{\mu _{\rm{e}}}E}} + {\alpha _y}\frac{h}{{{\mu _{\rm{e}}}E}}} \right)} $ |
| $ R\left( {{n_{{\rm{e}}h}}} \right) = \frac{{\partial {\varGamma _{{\rm{e}}x}}}}{{\partial x}} + \frac{{\partial {\varGamma _{{\rm{e}}y}}}}{{\partial y}} + \frac{{\partial {n_{{\rm{e}}h}}}}{{\partial t}} - {S_{\rm{i}}} - {S_{{\rm{ph}}}} $ |
式中, nel是有限元素的总数, neh是特征尺寸为h的有限元素中的电子密度, uh是对应的试函数. Γex和Γey是电子通量
| $ {{\alpha _x} = \coth \left( {P{e_x}} \right) - \left( {\frac{1}{{P{e_x}}}} \right),P{e_x} = \frac{1}{2}\frac{{{\mu _{\rm{e}}}\frac{{\partial \varPhi }}{{\partial x}}h}}{{{D_{\rm{e}}}}}} $ |
| $ {{\alpha _y} = \coth \left( {P{e_y}} \right) - \left( {\frac{1}{{P{e_y}}}} \right),P{e_y} = \frac{1}{2}\frac{{{\mu _{\rm{e}}}\frac{{\partial \varPhi }}{{\partial y}}h}}{{{D_{\rm{e}}}}}} $ |
将方程(3)以弱形式方程的方式代入COMSOL中电子密度输运方程弱形式, 即可得到稳定的解. 针对该改进的COMSOL模型, 具体的验证工作将在下节详细介绍.
2 基准验证与实验验证针对改进的COMSOL Multiphysics流注放电模型, 基于经典计算结果[16, 38]和实验结果[39]开展验证.
2.1 计算基准验证针板放电是一种经典和基础的等离子体放电结构, 国外前期开展了大量研究, 主要采用有限体积方法编程求解连续方程、Poisson方程与光电离. 其中, 俄罗斯科学院Kulikovsky等对针板放电开展了数值计算研究, 并构建了一系列便于验证的数值模拟基准算例. 文献[16]计算了1 cm间隙条件下, 大气压针板放电构型在13 kV恒定电压下的击穿过程, 考虑了电子碰撞电离反应、三体和双体吸附反应、电子-离子复合和离子-离子复合反应, 成功复现了雪崩-流注转捩现象和流注传播特性. 文献[16]的参数、方程完整详实, 得到了众多课题组的复现, 被国际上广泛认可为大气压低温等离子体数值计算的重要基准算例之一.
本文第1部分对比了使用标准有限元方法计算的结果与文献[16]的结果, 在图 1中展示了数值振荡和伪扩散问题. 本节使用修正后的COMSOL Multiphysics模型, 采用与文献[16]相同的控制方程、输运参数和反应体系再次开展计算, 结果如图 2所示.
|
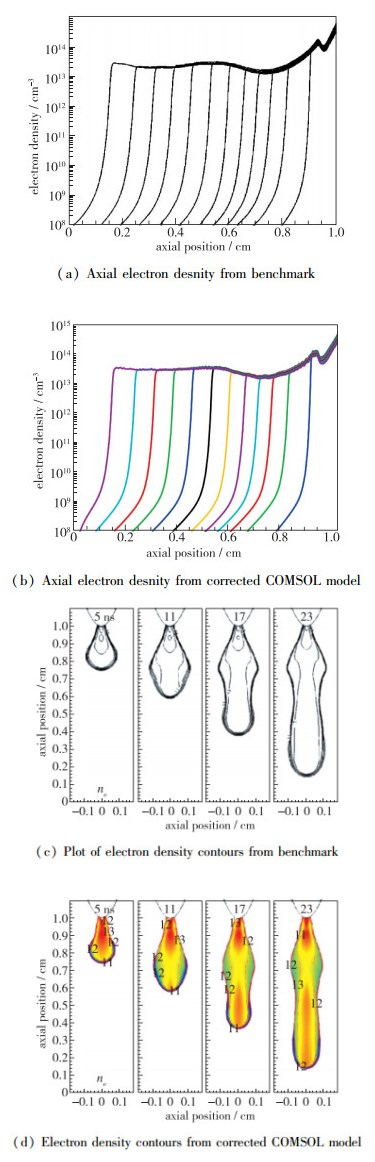
| 图 2 修正的COMSOL流注模型复现Kulikovsky基准流注算例[16] Fig.2 Results comparison between corrected COMSOL model and Ref[16] |
图 2(a)和(c)分别为文献[16]计算得到的不同时刻轴向电子密度分布和电子密度空间分布云图. 图 2(b)和(d)为采用修正COMSOL Multiphysics模型计算结果. 由图可见, 添加人工稳定性的修正模型计算结果与基准算例几乎没有区别: 电场强度、电子密度与传播过程均实现了准确的复现. 注意到使用修正COMSOL Multiphysics模型计算的流注直径比基准算例稍细, 引起这一区别的原因可能是光电离计算方式的不同: 文献[16]采用了简化的“积分环”方式, 仅计算流注头部强电场附近的光电离源项, 并将全局积分简化为对流注头部附近的环形体积进行积分. 本文采用了近年来使用较为广泛的Helmholtz三方程光电离模型[40], 该模型的准确性已经得到了广泛验证[41], 本文不再赘述. 图 1中基准算例的红线与图 2(a)(b)中左数第3条线(19 ns时刻)对应. 对比图 1,2可见, 修正后的模型计算结果中已经没有了图 1蓝线出现的数值振荡和伪扩散的问题.
需要注意的是, 本节进行的计算基准验证的核心目的是数值计算角度确保: 在相同的输运参数、几何结构和边界条件下, 求解相同的控制方程能够得到完全相同的解, 从而确保数值计算研究的一致性. 文献[16]的结果作为数值计算的良好基准, 却并未得到实验的充分验证. 在克服标准有限元方法引发的数值振荡、伪扩散问题的基础上, 使用修正的模型与实验结果进行了进一步比对验证.
2.2 实验结果验证利用修正后的COMSOL Multiphysics等离子体模型, 针对一例过电压实验进行直接比对[39]. 文献[39]利用相增强高速相机ICCD研究了大气压下, 1.6 cm间隙针板结构在纳秒脉冲过电压(86 kV)作用下的光学特性. 在实验(见图 3(a))和后续的计算中[42]均发现, 如果电压上升时间明显短于电场屏蔽效应的特征时间尺度, 局域场就会高于空气电离阈值, 引起独特的倒锥形放电结构.
|
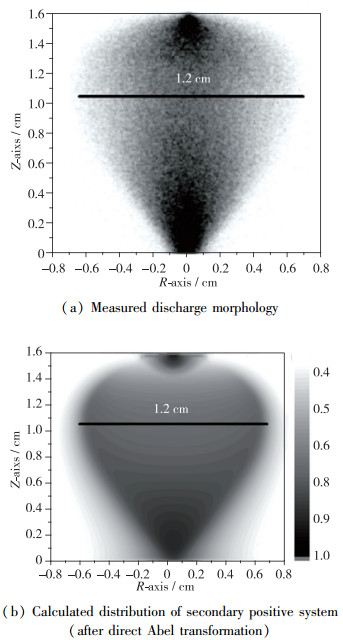
| 图 3 修正的COMSOL流注模型复现过电压放电实验 Fig.3 Overvoltage discharge experiment based on corrected COMSOL model |
在与实验完全相同的条件下, 本文试图利用标准有限元模型计算该倒锥形放电结构, 模型因为未知(黑盒子)原因不收敛, 未能完成计算. 本文仅展示了利用修正后的COMSOL Multiphysics等离子体模型的计算结果.
在实验中, 光学辐射的主要来源是氮气分子的第二正带系N2(C3Πu), 为此利用模型计算了该组分密度; 为了与实验测量结果直接对照, 对计算结果进行了Abel变换以考虑放电区域的厚度. 将变换后的计算结果在0~1之间进行归一化, 如图 3(b)所示. 实验和计算均捕捉到了阳极和阴极区域的局域强辐射, 以及在大约Z=1 cm处的最大放电直径1.2 cm, 实验结果与计算结果对比吻合良好.
3 结论针对商用有限元软件模拟流注放电时存在的数值问题, 推导了基于流线扩散人工稳定技术的修正项, 并在COMSOL Multiphysics软件中进行了测试. 计算发现, 采用标准有限元方法计算的针板流注结果存在显著的数值振荡和伪扩散流注问题, 而引入修正后的模型克服了这些数值问题, 能够成功复现1 cm气隙、13 kV电压条件下大气压空气流注基准算例. 进一步计算了1.6 cm气隙、86 kV过电压大气压空气放电形态,并与实验结果进行了对比验证, 证明了模型本身的可靠性. 计算与验证结果表明, 以弱形式偏微分方程的方式将人工稳定项引入基于有限元(标准Galerkin方法)的商用软件中, 能够有效克服放电计算中的数值振荡和流注伪扩散问题, 确保等离子体计算准确性和可重复性.
致谢 本文受到国家自然科学基金(51907204, 51790511, 91941105, 91941301)支持.| [1] |
Eliasson B, Kogelschatz U. Nonequilibrium volume plasma chemical processing[J]. IEEE Transactions on Plasma Science, 1991, 19(6): 1063-1077. DOI:10.1109/27.125031 |
| [2] |
Biederman H. Plasma polymer films[M]. Singapore: World Scientific, 2004.
|
| [3] |
Gusev V E, Karabutov A A. Laser optoacoustics[R]. NASA STI/Recon Tech. Rep. A, 1991: 93.
|
| [4] |
Kim H H. Nonthermal plasma processing for air-pollution control: a historical review, current issues, and future prospects[J]. Plasma Processes and Polymers, 2004, 1(2): 91-110. DOI:10.1002/ppap.200400028 |
| [5] |
Pilla G, Galley D, Lacoste D A, et al. Stabilization of a turbulent premixed flame using a nanosecond repetitively pulsed plasma[J]. IEEE Transactions on Plasma Sci-ence, 2006, 34(6): 2471-2477. DOI:10.1109/TPS.2006.886081 |
| [6] |
Massines F, Ségur P, Gherardi N, et al. Physics and chemistry in a glow dielectric barrier discharge at atmospheric pressure: diagnostics and modelling[J]. Surface and Coatings Technology, 2003, 174-175: 8-14. DOI:10.1016/S0257-8972(03)00540-1 |
| [7] |
Fridman A, Chirokov A, Gutsol A. Non-thermal atmospheric pressure discharges[J]. Journal of Physics D: Applied Physics, 2005, 38(2): R1-R24. DOI:10.1088/0022-3727/38/2/R01 |
| [8] |
Starikovskii A Y, Nikipelov A A, Nudnova M M, et al. SDBD plasma actuator with nanosecond pulse-periodic discharge[J]. Plasma Sources Science and Technology, 2009, 18(3): 034015. DOI:10.1088/0963-0252/18/3/034015 |
| [9] |
邵涛, 章程, 王瑞雪, 等. 大气压脉冲气体放电与等离子体应用[J]. 高电压技术, 2016, 42(3): 685-705. Shao T, Zhang C, Wang R X, et al. Atmospheric-pressure pulsed gas discharge and pulsed plasma applica-tion[J]. High Voltage Engineering, 2016, 42(3): 685-705. (in Chinese) |
| [10] |
李和平, 于达仁, 孙文廷, 等. 大气压放电等离子体研究进展综述[J]. 高电压技术, 2016, 42(12): 3697-3727. Li H P, Yu D R, Sun W T, et al. State-of-the-art of atmospheric discharge plasmas[J]. High Voltage Engineering, 2016, 42(12): 3697-3727. (in Chinese) |
| [11] |
Morrow R, Lowke J J. Streamer propagation in air[J]. Journal of Physics D: Applied Physics, 1997, 30(4): 614-627. DOI:10.1088/0022-3727/30/4/017 |
| [12] |
Boeuf J P, Pitchford L C. Pseudospark discharges via computer simulation[J]. IEEE Transactions on Plasma Science, 1991, 19(2): 286-296. DOI:10.1109/27.106826 |
| [13] |
Fiala A, Pitchford L C, Boeuf J P. Two-dimensional, hybrid model of low-pressure glow discharges[J]. Physical Review E, 1994, 49(6): 5607-5622. DOI:10.1103/PhysRevE.49.5607 |
| [14] |
Babaeva N Y, Naidis G V. Two-dimensional modelling of positive streamer dynamics in non-uniform electric fields in air[J]. Journal of Physics D: Applied Physics, 1996, 29(9): 2423-2431. DOI:10.1088/0022-3727/29/9/029 |
| [15] |
Babaeva N Y, Naidis G V. Dynamics of positive and negative streamers in air in weak uniform electric fields[J]. IEEE Transactions on Plasma Science, 1997, 25(2): 375-379. DOI:10.1109/27.602514 |
| [16] |
Kulikovsky A A. Positive streamer in a weak field in air: A moving avalanche-to-streamer transition[J]. Physical Review E, 1998, 57(6): 7066-7074. DOI:10.1103/PhysRevE.57.7066 |
| [17] |
Kulikovsky A A. A more accurate Scharfetter-Gummel algorithm of electron transport for semiconductor and gas discharge simulation[J]. Journal of Computational Physics, 1995, 119(1): 149-155. DOI:10.1006/jcph.1995.1123 |
| [18] |
Pechereau F, Jánsky J, Bourdon A. Simulation of the reignition of a discharge behind a dielectric layer in air at atmospheric pressure[J]. Plasma Sources Science and Technology, 2012, 21(5): 055011. DOI:10.1088/0963-0252/21/5/055011 |
| [19] |
Pancheshnyi S, Ségur P, Capeillère J, et al. Numerical simulation of filamentary discharges with parallel adaptive mesh refinement[J]. Journal of Computational Physics, 2008, 227(13): 6574-6590. DOI:10.1016/j.jcp.2008.03.020 |
| [20] |
Unfer T, Boeuf J P, Rogier F, et al. Multi-scale gas discharge simulations using asynchronous adaptive mesh refinement[J]. Computer Physics Communications, 2010, 181(2): 247-258. DOI:10.1016/j.cpc.2009.09.017 |
| [21] |
Ventzek P L, Hoekstra R J, Kushner M J. Two-dimensional modeling of high plasma density inductively coupled sources for materials processing[J]. Journal of Vacuum Science & Technology B: Microelectronics and Nanometer Structures Processing, Measurement, and Ph-enomena, 1994, 12(1): 461-477. |
| [22] |
Hagelaar G J, Kroesen G M. Speeding up fluid models for gas discharges by implicit treatment of the electron energy source term[J]. Journal of Computational Physics, 2000, 159(1): 1-12. DOI:10.1006/jcph.2000.6445 |
| [23] |
Lin K M, Hung C T, Hwang F N, et al. Development of a parallel semi-implicit two-dimensional plasma fluid modeling code using finite-volume method[J]. Computer Physics Communications, 2012, 183(6): 1225-1236. DOI:10.1016/j.cpc.2012.02.001 |
| [24] |
Unfer T, Boeuf J P, Rogier F, et al. An asynchronous scheme with local time stepping for multi-scale transport problems: Application to gas discharges[J]. Journal of Computational Physics, 2007, 227(2): 898-918. DOI:10.1016/j.jcp.2007.07.018 |
| [25] |
Li C, Teunissen J, Nool M, et al. A comparison of 3D particle, fluid and hybrid simulations for negative streamers[J]. Plasma Sources Science and Technology, 2012, 21(5): 055019. DOI:10.1088/0963-0252/21/5/055019 |
| [26] |
Chanrion O, Bonaventura Z, Cinar D, et al. Runaway electrons from a 'beam-bulk' model of streamer: applica-tion to TGFs[J]. Environmental Research Letters, 2014, 9(5): 055003. DOI:10.1088/1748-9326/9/5/055003 |
| [27] |
Babaeva N Y, Tereshonok D V, Naidis G V. Fluid and hybrid modeling of nanosecond surface discharges: effect of polarity and secondary electrons emission[J]. Plasma Sources Science and Technology, 2016, 25(4): 044008. DOI:10.1088/0963-0252/25/4/044008 |
| [28] |
Rauf S, Balakrishna A, Agarwal A, et al. Three-dimensional model of electron beam generated plasma[J]. Plasma Sources Science and Technology, 2017, 26(6): 065006. DOI:10.1088/1361-6595/aa6b49 |
| [29] |
Chanrion O, Neubert T. A PIC-MCC code for simulation of streamer propagation in air[J]. Journal of Computa-tional Physics, 2008, 227(15): 7222-7245. DOI:10.1016/j.jcp.2008.04.016 |
| [30] |
Levko D, Yatom S, Vekselman V, et al. Numerical simulations of runaway electron generation in pressurized gases[J]. Journal of Applied Physics, 2012, 111(1): 013303. DOI:10.1063/1.3675527 |
| [31] |
MacLachlan C S, Potts H E, Diver D A. Simulation of transient energy distributions in sub-ns streamer forma-tion[J]. Plasma Sources Science and Technology, 2013, 22(1): 015025. DOI:10.1088/0963-0252/22/1/015025 |
| [32] |
Teunissen J, Ebert U. 3D PIC-MCC simulations of discharge inception around a sharp anode in nitrogen/oxygen mixtures[J]. Plasma Sources Science and Technology, 2016, 25(4): 044005. DOI:10.1088/0963-0252/25/4/044005 |
| [33] |
Codina R, Oñate E, Cervera M. The intrinsic time for the streamline upwind/Petrov-Galerkin formulation using quadratic elements[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 94(2): 239-262. DOI:10.1016/0045-7825(92)90149-E |
| [34] |
Codina R. Comparison of some finite element methods for solving the diffusion-convection-reaction equation[J]. Computer Methods in Applied Mechanics and Enginee-ring, 1998, 156(1/4): 185-210. |
| [35] |
Codina R. On stabilized finite element methods for linear systems of convection-diffusion-reaction equations[J]. Computer Methods in Applied Mechanics and Enginee-ring, 2000, 188(1/3): 61-82. |
| [36] |
John V, Schmeyer E. Finite element methods for time-dependent convection-diffusion-reaction equations with small diffusion[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 198(3/4): 475-494. |
| [37] |
Codina R. Finite element approximation of the convection-diffusion equation: subgrid-scale spaces, local instabili-ties and anisotropic space-time discretizations[A]//Clavero C, Gracia J, Lisbona F. BAIL 2010-Boundary and Interior Layers, Computational and Asymptotic Methods[M]. Berlin: Springer, 2011: 85-97.
|
| [38] |
Pancheshnyi S, Nudnova M, Starikovskii A. Develo-pment of a cathode-directed streamer discharge in air at different pressures: experiment and comparison with direct numerical simulation[J]. Physical Review E, 2005, 71(1): 016407. DOI:10.1103/PhysRevE.71.016407 |
| [39] |
Tardiveau P, Moreau N, Bentaleb S, et al. Diffuse mode and diffuse-to-filamentary transition in a high pressure nanosecond scale corona discharge under high voltage[J]. Journal of Physics D: Applied Physics, 2009, 42(17): 175202. DOI:10.1088/0022-3727/42/17/175202 |
| [40] |
Bourdon A, Pasko V P, Liu N Y, et al. Efficient models for photoionization produced by non-thermal gas dischar-ges in air based on radiative transfer and the Helmholtz equations[J]. Plasma Sources Science and Technology, 2007, 16(3): 656-678. DOI:10.1088/0963-0252/16/3/026 |
| [41] |
蔡新景, 王新新, 邹晓兵, 等. 基于Helmholtz模型的流注放电过程光电离快速计算[J]. 中国电机工程学报, 2015, 35(1): 240-246. Cai X J, Wang X X, Zou X B, et al. Fast computation of photoionization in streamer discharges based on Helmholtz model[J]. Proceedings of the CSEE, 2015, 35(1): 240-246. (in Chinese) |
| [42] |
Pechereau F, Le Delliou P, Jánsky J, et al. Large conical discharge structure of an air discharge at atmospheric pressure in a point-to-plane geometry[J]. IEEE Transactions on Plasma Science, 2014, 42(10): 2346-2347. DOI:10.1109/TPS.2014.2309981 |



