我国经济的高速发展不可避免地带来了许多环境污染问题, 其中水污染是我国乃至整个世界范围内最为重要的环境污染问题之一.水污染的影响, 不仅破坏现有的环境, 而且会产生众多的社会问题.
污水处理在我国已成为迫在眉睫的问题, 对于不同类型的污水有不同的处理方法, 污水处理的物理方法有重力分离法、节流法、气浮法、离心法等.在众多的污水处理方法中, 气浮法是一种经济快捷又行之有效的方法.气浮法针对一些密度和水接近的细微颗粒, 因其自身质量难以在水中下沉或上浮, 可采用气浮装置, 将空气掺入污水中, 并使其以微气泡的形式由水中析出, 污水中密度接近水的微小颗粒状污染杂质吸附到气泡上, 并随气泡升至水面, 形成泡沫状的浮渣而去除[1].气浮法的关键在于产生微气泡及实现气液充分掺混.目前污水处理厂使用的微气泡产生器大多效率比较低, 产生的气泡多为效果较差的大气泡[2].
Venturi式气液掺混器因其结构简单, 成本低廉而被广泛用于气液掺混. Venturi式气液掺混器在产生微气泡, 实现气液充分掺混方面具有生成的气泡体积小且气液掺混效果稳定等众多优势.提高Venturi式气液掺混器的掺混效果, 对于污水治理具有重要意义和重大经济价值.
因此, 本次主要通过改变Venturi式气液掺混器的结构几何参数, 探究各个几何参数对掺混性能的影响, 进而优化气液掺混性能.
1 研究现状国外对于Venturi式掺混器的研究起步较早, Barre等进行了相关的实验和数值仿真来分析在Venturi管几何结构中的两相流结构.研究采用新的双光学探头测量, 并开发了特殊的数据处理方法来估计冷空气流的空隙率和速度场.通过应用新的计算方法, 提出了基于实验和数值结果比较的局部和全局分析[3]. Uesawa等研究了Venturi管中微气泡生成的机制.为了揭示气泡破裂现象的机制, 他们详细地观察了Venturi管中的气泡行为, 并测量了流动方向上的压力和空隙率.通过使用测量结果, 估计气液混合速度、声速和Mach数.在实验结果中, 气泡一旦扩张到Venturi管的扩散区域, 就会迅速收缩并分解成大量小小的气泡. Venturi管喉部周围的压力急剧下降, 而在气泡破裂的区域压力逐渐恢复[4]. Nomura等研究了Venturi管在气泡破裂行为上一些未解决的流动结构问题.重新描述了Venturi管中的气泡破裂机理.该研究使用高速摄像机详细观察气泡的变化, 观察到在低速条件下, 气泡分裂成几个部分, 流体从气泡的下游穿透到上游.在高速条件下, 气泡破碎成无数微气泡, 伴随剧烈的气泡膨胀和收缩.另外, 详细测量了压力分布, 压力分布图显示出Venturi管中存在超声速流动的趋势, 并且扩张部分出现了逐渐恢复的压力梯度.气泡裂变点与压力恢复点之间有很强的相关性.因此认为气泡破碎受到发散部分压力恢复的强烈影响[5].
王淼等采用CFD的数值计算方法,通过探究喉道直径、收缩段长度、凹槽直径、凹槽位置等结构参数对性能影响[6],马宁宁计算了进口的溶解氧浓度、进口水流速度、开孔直径大小、断面收缩比以及开孔Venturi管下游长度等条件不同时,开孔Venturi管气液两相混合物的溶解氧恢复系数和混合流出口处的气体体积分数.发现气液混合后,受重力的影响,管道上部的气体体积分数较大,不利于水体增氧[7]. Kaneko等研究了使用气泡流进入Venturi管的有效技术,他认为发散部分的压力变化引起气泡破裂[9].国内学者岳伟挺第一次把气液两相流文丘里管的差压波动信号与空隙率进行了关联性研究[10].李鹏等为了建立高固气比的气体粉煤混合物流经Venturi管收缩段的压降模型,分析了在密相气力输送系统中Venturi管收缩段内的压降组成,包括气相造成的压降与固相造成的压降,气相加速压降与固相加速压降,得到在一定的工艺操作参数下,模型预测不同收缩角对应的收缩段压降值与实验值吻合较好[11].唐文偲利用高速摄像系统跟踪气泡的运动和碎化过程,分析气液相流速对碎化后气泡尺寸的影响[12].
Cui等研究了气泡破裂过程中冰破裂、气泡射流和冲击波的特征[13]. Peining等基于两相流体动力学,分别对气相与液相流动进行分析研究,分析了截面含气率、相间摩擦及液滴夹带等因素对流量测量的影响,分别建立了分层流、环状流下的水平标准Venturi流量计的理论模型[14]. Fujiwara等通过可视化和其他测量方法研究了气泡破碎现象,认为气泡破碎可能是由于超声速流向亚声速流过渡引起的压力冲击造成的[15]. Yin等将气体体积比的影响加在相关性上,指出体积平均气泡直径与气体体积比成线性关系[16]. Gordiychuk等也调查了空气和水的流量以及空气入口尺寸是如何影响Venturi型气泡发生器的微气泡尺寸分布,并得出结论:气泡的大小同水流的速度成反比关系,空气与水的比例也会导致气泡尺寸增加[17]. Kress在美国的橡树岭国家实验室开发了一种可行且简单的气泡发生器——Venturi型气泡发生器,在这种气泡发生器的作用下,可以将大气泡破碎为小气泡[18].
国内也有众多学者针对Venturi式气泡发生器进行了研究.颜攀等[19]提出了使用Venturi气泡发生器的微鼓泡反应器,并以实验的方法探究了进气孔位置等因素对气泡平均直径的影响,曹俊雅等[20]探究了进气方向对Venturi微气泡发生器气泡直径的影响,谢菲等[21]通过数值模拟以及实验的方式探究了文丘里管内气固两相流动的情况,莫政宇等[22]利用可视化研究方法研究了Venturi式气泡发生器内气泡输运过程.
国内外学者已经研究了Venturi式气液掺混器的气泡破碎机制以及进气孔直径、断面收缩比、出口段长度等结构参数对掺混性能的影响, 但是对于不同收缩段曲线、进气孔数量及扩张角角度与掺混性能之间的关系还缺乏研究.基于以上研究背景和研究现状, 本文主要研究Venturi式掺混器收缩段曲线、进气孔数量及扩张角对气液掺混性能的影响, 通过比较不同模型所得的出口段气体体积分数、沿轴向压力变化及沿轴向湍动能变化, 得出较佳的几何参数.
2 数值模拟研究方法流体的流动、热量的传递都要遵循质量守恒、动量守恒和能量守恒等基本物理定律.控制方程是对这些基本物理定律的数学描述, 将流体的运动和热量的转移等基本规律用数学语言描述出来就构成了流动和传热的基本控制方程.在理论研究、实验研究存在诸多限制的情况下, 数值模拟作为一种离散近似的计算方法, 能够低成本高效地预测流体现象.而且, 随着计算流体力学(CFD)的不断发展和完善, 数值模拟已成为研究各种复杂物理现象的有效手段之一[11].
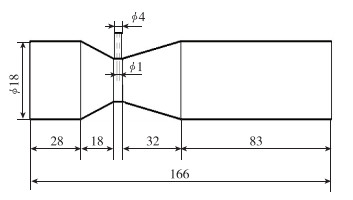
2.1 物理模型采用CATIA三维建模软件建立了Venturi式掺混器的物理模型.模型进出口尺寸的预先设计主要考虑方便未来实验及安装水流接口, 预设进口段及出口段直径均为18 mm, 壁厚为1 mm.全管总长预设为166 mm.进出口外部均设计了增阻层, 用于实验时进出口水流接口的良好安装.
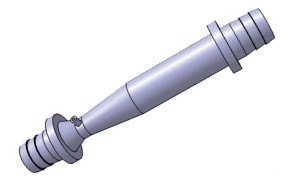
建立的Venturi式气液两相掺混器三维模型如图 1所示, 模型几何参数如图 2所示.
|
| 图 1 Venturi式掺混器物理模型 Fig.1 Physical model of Venturi mixer |
|
| 图 2 Venturi式掺混器几何参数(单位: mm) Fig.2 Geometric parameters of Venturi mixer(unit: mm) Note: shrinkage curve, number of intake holes and angle of expansion are single variables of each model, which are not listed in the table |
使用ICEM软件生成网格,块划分采用O-Block划分,进行网格及切块修正,生成并转换为如图 3所示的非结构网格,为导入ANSYS FLUENT做好准备.

|
| 图 3 全局网格 Fig.3 Global Grids |
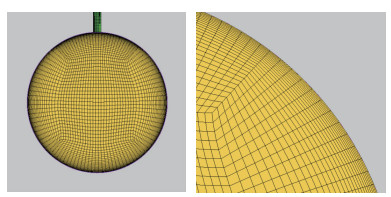
数值模拟结果的准确度很大程度上取决于网格质量的好坏.当流动有阻碍, 迫使流体流动方向发生突变、绕流等情况时, 流场会伴随出现一些复杂的涡系.此时网格太稀疏会使计算精度下降, 无法呈现流动的细节.因此, 为了更准确地捕捉这些流动信息, 就须对这些区域的网格加密, 如图 4所示.
|
| 图 4 网格局部加密 Fig.4 Local mesh encryption |
因为本文主要研究Venturi式掺混器内部气液两相的掺混程度, 根据居晓峰等的研究[8], 水流量较高(16~20 m3/h)时, 标准k-ε模型数值模拟结果与实验结果误差较小, 而本文研究的水流量设置为18.3 m3/h, 水流速度为2 m/s. Reynolds数为
| $ Re = \frac{{\rho \upsilon d}}{\mu } $ |
计算得出本文喉道Reynolds数为3 074, 因此喉道内流动为湍流, 故而选用标准k-ε模型[14];采用SIMPLEC算法进行求解.其余参数及边界条件设置如表 1所示.
| 下载CSV 表 1 边界条件表 Tab.1 Boundary conditions |
运用控制单一变量法, 分析不同收缩段曲线对气液掺混性能的影响, 观测指标选用由Tecplot所导出的出口段气体体积分数图、由Matlab所导出的压力变化图及湍动能变化图.
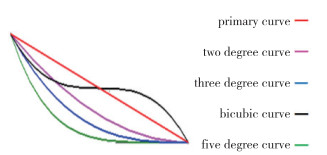
3.1 收缩段曲线介绍本次研究选用几种经典曲线进行研究, 分别为一次直线、二次曲线、三次曲线、五次曲线、双三次曲线.各曲线方程如下:
一次直线 y = 4.5x
二次曲线
三次曲线
双三次曲线
五次曲线
不同曲线的线形见图 5.
|
| 图 5 不同曲线线型对比图 Fig.5 Comparisons of different curves and lines |
不同收缩段曲线数值模拟所得气体体积分数如图 6所示.
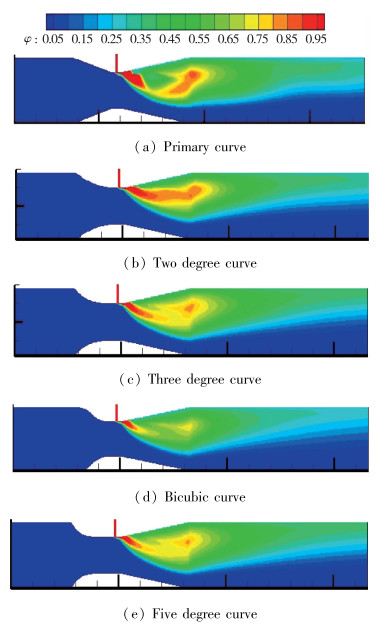
|
| 图 6 不同收缩段曲线所得气体体积分数图 Fig.6 Volume fraction diagrams of gases obtained from different contraction curves |
图 6(a)为一次直线数值模拟所得气体体积分数云图, 出口段气体体积分数在15%~25%的长度为2.9 mm, 25%~35%的长度为6.8 mm;图 6(b)为二次曲线数值模拟所得气体体积分数云图, 出口段气体体积分数在15%~25%的长度为2.8 mm, 气体体积分数在25%~35%的长度为5.6 mm;图 6(c)为三次曲线数值模拟所得气体体积分数云图, 出口段气体体积分数在15%~25%的长度为2.7 mm, 气体体积分数在25%~35%的长度为3 mm, 气体体积分数在35%~45%的长度为2.6 mm;图 6(d)为双三次曲线数值模拟所得气体体积分数云图, 出口段气体体积分数在15%~25%的长度为4 mm, 气体体积分数在25%~35%的长度为3.2 mm;图 6(e)为五次曲线数值模拟所得气体体积分数云图, 出口段气体体积分数在15%~25%的长度为2.7 mm, 气体体积分数在25%~35%的长度为3.3 mm, 气体体积分数在35%~45%的长度为2.6 mm.
将各收缩段曲线不同的模型数值模拟所得气体体积分数图汇总得到图 7.
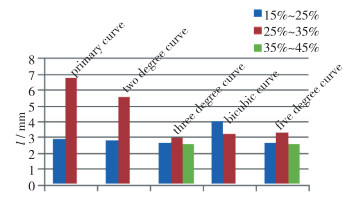
|
| 图 7 不同收缩段曲线气体体积分数对比 Fig.7 Comparisons of gas volume fractions in different contraction sections |
如图 7所示, 在所选5条曲线中, 一次直线掺混所得的气体体积分数较低的长度最长, 三次曲线和五次曲线所得数值模拟结果相近, 气体体积分数在35%~45%的长度在5组曲线中最长, 表明三次曲线和五次曲线的出口段气含率最高, 推测气含率与气泡直径有关, 因此三次曲线和五次曲线的气液掺混所得气泡直径较大, 一次直线和双三次曲线仿真所得的出口段气体体积分数较低, 则一次直线和双三次曲线气液掺混所得气泡直径较小.因此, 在所选的5条曲线中, 由气体体积分数图可得, 一次直线和双三次曲线的气液掺混效果最好, 下文依据压力变化和湍动能数值进行分析.
3.3 不同收缩段曲线的压力对比将不同收缩段曲线数值模拟所得数据导入Matlab获得如图 8所示的沿轴向压力变化图.
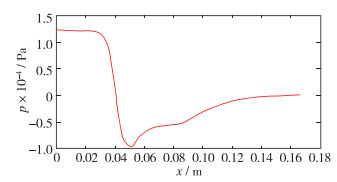
|
| 图 8 双三次收缩段曲线沿轴向压力变化 Fig.8 Change of axial pressure along the contraction section of bicubic curve |
如图 8所示, 以双三次曲线作为收缩段为例, 水流从入口段进入Venturi式掺混器, 受壁面摩擦等因素影响, 压力缓慢降低, 到收缩段, 横截面积减小, 流速增大, 压力显著降低至负压, 喉道处产生内外压差, 将空气吸入管内, 由于空气的进入, 管内压力略有恢复, 但是数值较小.到扩张段, 横截面积增大, 流速减小, 压力逐渐恢复, 最终在管道出口处压力恢复至大气压. 图 8验证了Venturi式掺混器的工作原理:压力的降低导致空气被吸入Venturi式掺混器, 压力恢复所引起的剪切力使气泡破碎, 湍流作用使气液掺混.将不同曲线所得压力变化图用Matlab合并得到图 9.
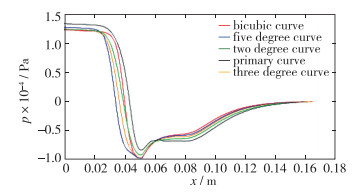
|
| 图 9 不同收缩段曲线压力变化比较 Fig.9 Comparisons of pressure variations in different contraction sections |
如图 9所示, 入口处一次直线的压力最高, 出口段5条曲线压力均恢复为标准大气压, 表明除了壁面摩擦影响之外, 一次直线的压力恢复最强, 吸入的空气最多.在扩张段5条曲线的压力均迅速回升, 观察扩张段压力恢复曲线对比, 也是一次直线的压力回升最迅速.因此, 由不同曲线的压力变化比较可总结出:一次直线的气泡破碎效果最好, 气液掺混性能应该最佳.下面结合湍动能变化图进行分析.
3.4 不同收缩段曲线的湍动能对比将数值模拟所得不同收缩段曲线的数据导入Matlab获得如图 10所示的湍动能变化图.
|
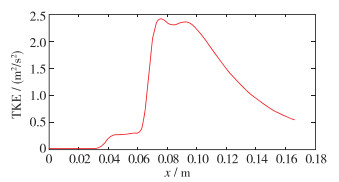
| 图 10 双三次收缩段曲线湍动能变化图 Fig.10 Turbulence kinetic energy change chart of bicubic curve |
如图 10所示湍动能变化图, 以双三次曲线收缩段为例, 水流从入口段进入掺混器时为层流, 流体的湍动能为0, 到达喉道之后, 由于空气的加入, 湍流程度加强, 湍动能略增大, 但是效果不明显, 到达扩张段时, 由于压力迅速回升引起的湍动程度加剧, 湍动能迅速增大到最大值, 随后气泡破碎与水流混合, 湍动能逐渐降低.因为本文研究的出口段长度不够, 湍动能未能减小到0.将不同收缩段曲线的湍动能变化图用Matlab汇总得到图 11.
|
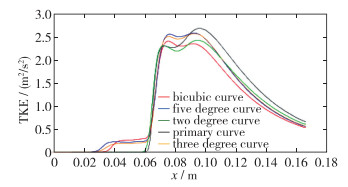
| 图 11 不同收缩段曲线湍动能对比 Fig.11 Comparisons of turbulent energy in different contraction curves |
如图 11所示, 在扩张段, 5条曲线的湍动能均迅速增大, 但是增大的幅度不同, 表明湍流剧烈程度不同, 其中二次曲线、三次曲线和双三次曲线的湍动能增大较低, 而一次直线和五次曲线的湍动能增大值最大, 一次曲线的峰值最高, 表明一次直线的湍流程度最剧烈.由湍动能对比图表明, 一次直线的气液掺混效果最好.
3.5 小结首先介绍了不同收缩段曲线的曲线方程及图像对比, 接着对仿真所得数据通过气体体积分数、压力变化图及湍动能变化图的对比, 分析得出5条收缩段曲线中气液掺混性能最佳的曲线.分析气体体积分数对比时, 由局部气含率分析, 得出一次直线和双三次曲线的局部气含率最为均匀, 因此气体体积分数的对比得出一次直线和双三次曲线的气液掺混效果最佳;针对压力变化结果, 本文由压力恢复的大小和扩张段压力恢复的剧烈程度, 判断一次直线的压力恢复数值最大, 且在扩张段压力恢复最剧烈, 因此一次直线的气泡剪切效果最好, 气液掺混效果也最好;针对湍动能变化结果, 本文由湍动能上升及下降剧烈程度和湍动能峰值大小比较, 得出一次直线的湍动能峰值最大, 且在扩张段湍动能上升最迅速, 表明一次直线的扩张段湍流程度最高, 气液掺混效果最好.综合上述3个不同角度的比较得出:在所选用的5条收缩段曲线中, 一次直线的气液掺混性能最佳.居晓峰等[8]在Venturi式气泡发生器工作特性分析中做过类似实验, 本章数值仿真分析所得的结果与其相符合.
4 进气孔数量对掺混性能的影响 4.1 进气孔数量及分布介绍运用控制单一变量法分别模拟了1, 2, 4个进气孔数目对Venturi式气液掺混器掺混性能的影响.模拟2个进气孔时进气孔在同一平面对称排布, 如图 12(a)所示;模拟4个进气孔时, 4个进气孔在同一平面绕喉道环形排列, 如图 12(b)所示.
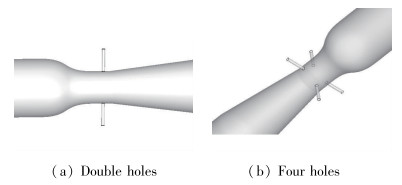
|
| 图 12 进气孔数量及分布 Fig.12 Number and distributions of inlet holes |
将不同进气孔数目所得仿真数据导入Tecplot和Matlab中, 获得气体体积分数图和压力变化图、湍动能变化图.
4.2 不同进气孔数量的气体体积分数比较图 13分别是1, 2, 4个进气孔条件下, 数值模拟所得的气体体积分数图. 图 13(a)中, 出口段气体体积分数在15%~25%的长度为4 mm, 气体体积分数在25%~35%的长度为3.5 mm;图 13(b)为2个进气孔时的气体体积分数图, 因受重力影响, 位于下方的进气孔吸入的空气与位于上方的进气孔吸入的空气未能实现良好的掺混, 由图 13(b)可以看出, 2个进气孔时的出口段气体体积分数显著高于1个进气孔时, 本文认为是由于2个进气孔的进气量大于1个进气孔的进气量, 进而2个进气孔的气液掺混性能也就优于1个进气孔时的掺混性能;图 13(c)为4个进气孔的出口段气体体积分数图, 由Tecplot测得其出口段气体体积分数基本位于35%~45%之间, 气液掺混非常充分.
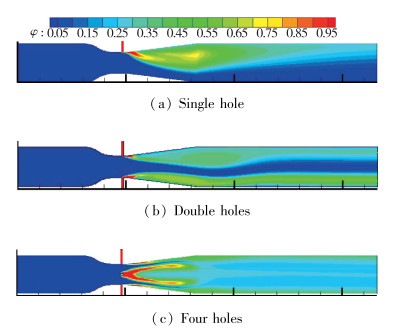
|
| 图 13 不同进气孔数量的气体体积分数 Fig.13 Volume fractions of gas with different number of intake holes |
将数值模拟所得不同进气孔数目的数据导入Matlab获得如图 14所示的压力变化图.
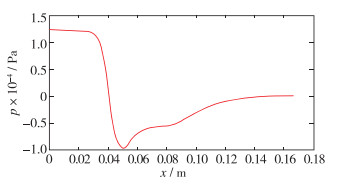
|
| 图 14 两个进气孔所得压力变化图 Fig.14 Pressure variation diagram of two inlet holes |
与不同收缩段曲线所得的压力变化图分析类似,以带有2个进气孔的掺混器为例,如图 14所示为2个进气孔工况下的压力变化图.将不同进气孔数量模型计算所得压力变化图用Matlab合并得到图 15.
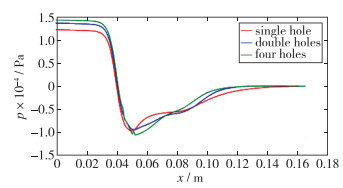
|
| 图 15 不同进气孔数目所得压力变化图对比 Fig.15 Comparisons of pressure change diagrams of different inlet hole numbers |
如图 15所示, 入口处压力4个进气孔的压力最高, 出口段3个模型的压力均恢复为标准大气压, 表明除了壁面摩擦影响之外, 4个进气孔模型的压力恢复最强, 吸入的空气最多, 气液掺混效果最好.在扩张段3个模型的压力均迅速回升, 由居晓峰等[19]的研究表明:压力的迅速回升将加速气泡碎化的过程, 压力恢复越迅速, 气泡碎化越充分.观察扩张段压力恢复曲线对比, 也是4个进气孔模型的压力回升最迅速.因此, 由压力变化对比图得出, 4个进气孔得到掺混性能优于单进气孔和双进气孔的模型.下面观察3个模型的湍动能对比.
4.4 不同进气孔数目的湍动能变化对比将数值模拟所得不同收缩段曲线的数据导入Matlab获得如图 16所示的湍动能变化图.
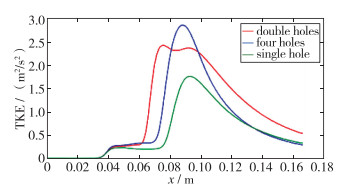
|
| 图 16 不同进气孔数目所得湍动能对比图 Fig.16 Turbulent kinetic energy comparison diagram with different numbers of intake holes |
如图 16所示,在扩张段,3个模型的湍动能均迅速增大,很显然在4个孔同时引入气流时对管内主流带来的扰动最大,1个孔工况下扰动则最小.由湍动能对比图表明,4个进气孔模型的气液掺混效果最好.
4.5 小结首先介绍了不同进气孔数目的位置及分布, 接着分析气体体积分数对比时, 由局部气含率分析,得出4个进气孔数目的局部气含率最为均匀;分析压力变化对比时,由压力恢复的大小和扩张段压力恢复的剧烈程度上来看,4个进气孔模型的压力恢复数值最大恢复速率快,因此得出4个进气孔模型的气泡剪切效果最好的结论;分析湍动能变化对比时, 由湍动能升降的剧烈程度和湍动能峰值大小比较, 发现4个进气孔模型的湍动能峰值最大, 且在扩张段湍动能上升最迅速, 表明4个进气孔模型的扩张段湍流程度最高, 气液掺混效果最好.
5 扩张角对掺混性能的影响 5.1 扩张角介绍本次研究初步选择扩张角为7.5°建立第1个模型, 然后在此基础上增大1.5°使扩张角为9°;减小1.5°, 使扩张角为6°, 对3个模型进行数值模拟, 分析得出气体体积分数图、压力变化图、湍动能变化图.扩张角示意图如图 17所示.
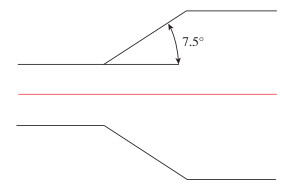
|
| 图 17 扩张角示意图 Fig.17 Expansion angle diagram |
将不同进气孔数目所得仿真数据导入Tecplot和Matlab中, 获得气体体积分数图和压力变化图、湍动能变化图.
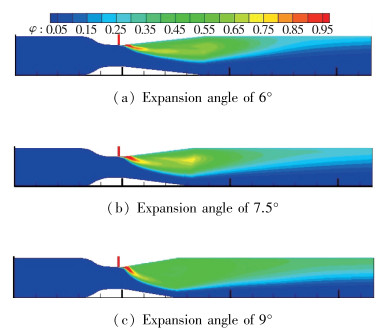
5.2 不同扩张角所得气体体积分数图 18中为不同扩张角时的气体体积分数截面图, 保持水流速度, 空气压力入口及其他一切条件都相同, 测量出口段气体体积分数分布情况. 图 18(a)中, 扩张角为6°时, 掺混器出口处气体体积分数在15%~25%的长度为3.7 mm, 气体体积分数在25%~35%的长度为0.7 mm;图 18(b)扩张角为7.5°时, 出口处气体体积分数在15%~25%的长度为3 mm, 气体体积分数在25%~35%的长度为3.1 mm;图 18(c)扩张角为9°时, 出口段气体体积分数在15%~25%的长度为2.7 mm, 在25%~35%的长度为3.8 mm, 在35%~45%的长度为3 mm.将3个扩张角所得出口段气体体积分数整理得图 19.
|
| 图 18 不同扩张角得出的积分数图 Fig.18 Integral plot with different expansion angles |
|
| 图 19 不同扩张角角度所得气体体积分数比较 Fig.19 Comparisons of gas volume fractions at different expansion angles |
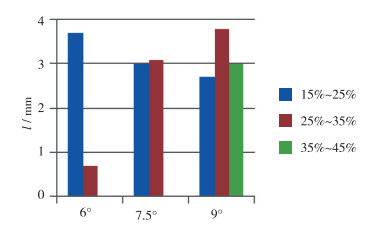
如图 19所示, 在研究所选3个扩张角中, 6°扩张角掺混所得的气体体积分数较低的长度最长, 9°扩张角数值模拟所得35%~45%段长度最长, 表明9°扩张角模型的出口段气含率最高, 其他条件相同的情况下, 表明9°扩张角喉道吸入的空气最多, 因此9°扩张角的局部气含率最高, 由气体体积分数图分析所得的气液掺混性能也最好.下文依据压力变化和湍动能数值进行分析.
5.3 不同扩张角所得压力云图将数值模拟所得不同收缩段曲线的数据导入Matlab获得如图 20所示的压力变化图.
|
| 图 20 扩张角为6°模型的压力变化图 Fig.20 Pressure change chart of model with expansion angle of 6° |
其变化趋势与其它工况大致一样,都是呈现在收缩段急剧下降,而在扩张段开始缓慢回升.将不同曲线所得压力变化图用Matlab合并得到图 21.
|
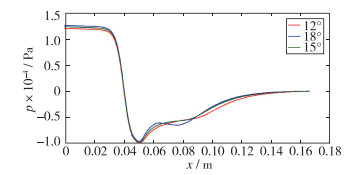
| 图 21 不同扩张角所得压力变化图比较 Fig.21 Comparisons of pressure diagram at different expansion angles |
如图 21所示, 入口处扩张角为9°的的压力最高, 出口段3个模型的压力均恢复为标准大气压, 表明除了壁面摩擦影响之外, 扩张角为9°的压力恢复最强, 吸入的空气最多, 气液掺混效果最好.在扩张段3个模型的压力均迅速回升, 观察扩张段压力恢复曲线, 发现扩张角为9°的模型的压力回升最迅速.因此, 作者由压力变化对比图得出, 扩张角为9°的模型得到掺混性能优于扩张角为6°的模型和扩张角为7.5°的模型.下面观察3个模型的湍动能对比.
5.4 不同扩张角所得湍动能图将不同收缩段曲线的湍动能变化图用Matlab汇总得到图 22.
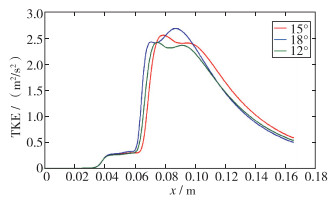
|
| 图 22 不同扩张角所得湍动能对比图 Fig.22 Comparisons of turbulent energy at different expansion angles |
如图 22所示,在扩张段,1, 2, 4孔模型的湍动能均迅速增大,但是增大的幅度不同,其中扩张角为6°模型的湍动能增大较低, 而扩张角为7.5,9°模型的湍动能增大较多, 且在扩张段的增大速度来看, 扩张角为7.5,9°的模型增大速度比扩张角为6°模型的速度大, 表明扩张角为9°模型的湍流程度提高的最快, 并且扩张角为9°模型的湍动能峰值最高, 表明扩张角为9°模型的湍流程度最剧烈.因此由湍动能对比图表明, 扩张角为9°模型的气液掺混效果最好.
5.5 小结首先介绍了不同扩张角的大小, 通过对3种模型的气体体积分数的分析,得出扩张角为9°模型的局部气含率最高, 因此模型的气液掺混效果最佳;分析压力变化对比时, 从压力恢复程度和速率上来看,扩张角为9°模型的气泡剪切效果最好, 气液掺混效果也最好;分析湍动能变化对比时, 由湍动能升降的剧烈程度和湍动能峰值大小比较, 得出扩张角为9°模型的湍动能峰值最大, 且在扩张段湍动能上升最迅速, 表明该模型的扩张段湍流程度最高,值得注意的是,在本文所研究范围内, 随着扩张角的增大, 气液掺混性能逐渐提高.
6 结论本文首先介绍了CFD数值模拟方法, 并确定了采用数值模拟方法研究Venturi式掺混器结构几何参数对其掺混性能的影响.研究了收缩段曲线、进气孔数目及扩张角对掺混性能的影响.通过综合对比出口段气体体积分数、压力变化图、湍动能变化图, 得出了本文研究范围内的最佳参数.
(1) 收缩段曲线为一次直线时, 掺混性能在所选5条曲线中最佳, 由湍动能变化图分析得出这是湍动能和压力变化引起的剪切力最大造成的.
(2) 研究不同进气孔数量对掺混性能的影响时, 本文由1,2,4个进气孔之间掺混效率的关系, 发现在本文研究的进气孔数目范围内, 随着进气孔数目的增加, 气液掺混性能逐渐提高.
(3) 研究了扩张角变化对掺混效率的影响时, 分析得出, 在6~9°的范围内, 随着扩张角角度的增大, 气液掺混效率随之显著增大.
| [1] |
田银令. 水环境污染的控制技术方法[J]. 科技风, 2013(1): 212. DOI:10.3969/j.issn.1671-7341.2013.01.188 |
| [2] |
管金发, 邓松圣, 张攀峰, 等. 文丘里管空化装置设计与数值模拟[J]. 后勤工程学院学报, 2012, 28(3): 30-34. Guan J F, Deng S S, Zhang P F, et al. Design and numerical simulation of Venturi tube hydrodynamic cavitation equipment[J]. Journal of Logistical Engineering Univer-sity, 2012, 28(3): 30-34. DOI:10.3969/j.issn.1672-7843.2012.03.007 (in Chinese) |
| [3] |
Barre S, Rolland J, Boitel G, et al. Experiments and modeling of cavitating flows in Venturi:attached sheet cavitation[J]. European Journal of Mechanics-B/Fluids, 2009, 28(3): 444-464. DOI:10.1016/j.euromechflu.2008.09.001 |
| [4] |
Uesawa S I, Kaneko A, Nomura Y, et al. Study on bubble breakup behavior in a Venturi tube[J]. Multi-phase Science and Technology, 2012, 24(3): 257-277. DOI:10.1615/MultScienTechn.v24.i3 |
| [5] |
Nomura Y, Uesawa S I, Kaneko A, et al. Study on bubble breakup mechanism in a Venturi tube[C]. Proceedings of ASME-JSME-KSME 2011 Joint Fluids Engineering Conference, Hamamatsu: ASME, 2011: 2533-2540.
|
| [6] |
王淼, 黄兴法, 李光永. 文丘里施肥器性能数值模拟研究[J]. 农业工程学报, 2006, 22(7): 27-31. Wang M, Huang X F, Li G Y. Numerical simulation of characteristics of Venturi Injector[J]. Transactions of the CSAE, 2006, 22(7): 27-31. DOI:10.3321/j.issn:1002-6819.2006.07.006 (in Chinese) |
| [7] |
马宁宁.开孔文丘里管掺气水流的水力和增氧特性研究[D].青岛: 中国海洋大学, 2015. Ma N N. Hydraulic and reoxygenation of characteristic research on aeration flow in Venturi tube with perforates[D]. Qingdao: Ocean University of China, 2015(in Chinese). |
| [8] |
居晓峰, 孙立成, 唐文偲, 等. 文丘里式气泡发生器工作特性分析[J]. 核技术, 2014, 37(12): 67-72. Ju X F, Sun L C, Tang W C, et al. Analysis of the operating characteristics of a Venturi-type bubble generator for MSR[J]. Nuclear Techniques, 2014, 37(12): 67-72. (in Chinese) |
| [9] |
Kaneko A, Nomura Y, Shu T, et al. Bubble break-up phenomena in a Venturi tube[J]. Nihon Kikai Gakkai Ronbunshu B Hen/transactions of the Japan Society of Mechanical Engineers Part B, 2007, 78(786): 207-217. |
| [10] |
岳伟挺.基于文丘里管的气液两相流参数检测方法研究[D].杭州: 浙江大学, 2004. Yue W T. Research on gas-liquid two-phase flow parameters measurement with Venturi tube[D]. Hangzhou: Zhejiang University, 2004(in Chinese). |
| [11] |
李鹏, 陆海峰, 郭晓镭, 等. 文丘里管收缩段高固气比气固两相流压降模型[J]. 化学工程, 2017, 45(6): 39-43. Li P, Lu H F, Guo X L, et al. Pressure drop model for gas/solid flow in contraction section of Venturi with high solid-gas ratio[J]. Chemical Engineering(China), 2017, 45(6): 39-43. DOI:10.3969/j.issn.1005-9954.2017.06.008 (in Chinese) |
| [12] |
唐文偲, 阎昌琪, 孙立成, 等. 文丘里式气泡发生器气泡碎化特性研究[J]. 原子能科学技术, 2014, 48(5): 844-848. Tang W C, Yan C Q, Sun L C, et al. Characteristic of bubble breakup in Venturi-type bubble generator[J]. Atomic Energy Science and Technology, 2014, 48(5): 844-848. (in Chinese) |
| [13] |
Cui P, Zhang A M, Wang S P, et al. Ice breaking by a collapsing bubble[J]. Journal of Fluid Mechanics, 2018, 841: 287-309. DOI:10.1017/jfm.2018.63 |
| [14] |
YU P N, XU Y, ZHANG T, et al. A study on the modeling of static pressure distribution of wet gas in Ven-turi[J]. Aiche Journal, 2015, 61(2): 699-708. DOI:10.1002/aic.14657 |
| [15] |
Fujiwara A, Takagi S, Matsumoto Y. Bubble breakup phenomena in a venturi tube[C]. ASME/JSME 2007, Joint Fluids Engineering Conference, 2007: 553-560.
|
| [16] |
Yin J, Li J, Li H, et al. Experimental study on the bubble generation characteristics for an Venturi type bubble generator[J]. International Journal of Heat & Mass Transfer, 2015, 91: 218-224. |
| [17] |
Gordiychuk A, Svanera M, Benini S, et al. Size distribution and Sauter mean diameter of micro bubbles for a Venturi type bubble generator[J]. Experimental Thermal & Fluid Science, 2016, 70: 51-60. |
| [18] |
Kress T S. Mass transfer between small bubbles and liquids in cocurrent turbulent pipeline flow. Tennessee University, Knoxville, 1972.
|
| [19] |
颜攀, 黄正梁, 王靖岱, 等. 文丘里气泡发生器的气泡尺寸及分布[J]. 浙江大学学报(工学版), 2017, 51(10): 2070-2076. Yan P, Huang Z L, Wang J D, et al. Bubble size and distribution of Venturi bubble generator[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(10): 2070-2076. DOI:10.3785/j.issn.1008-973X.2017.10.023 (in Chinese) |
| [20] |
曹俊雅, 马梦杰, 李平平, 等. 进气方向对文丘里微气泡发生器气泡直径的影响[J]. 黄金科学技术, 2017, 25(5): 127-134. Cao J Y, Ma M J, Li P P, et al. Effect of air intake direction on bubble diameter of Venturi microbubble generator[J]. Gold Science and Technology, 2017, 25(5): 127-134. (in Chinese) |
| [21] |
谢菲, 吴占松. 文丘里管内气固两相流动的数值模拟和实验[J]. 动力工程学报, 2007, 27(2): 237-241. Xie F, Wu Z S. Numerical simulation and experiment of gas-solid two-phase flow in Venturi tubes[J]. Journal of Power Engineering, 2007, 27(2): 237-241. (in Chinese) |
| [22] |
莫政宇, 杜敏, 邵梓一, 等. 文丘里式气泡发生器内气泡输运过程研究[J]. 原子能科学技术, 2016, 50(6): 1034-1039. Mo Z Y, Du M, Shao Z Y, et al. Study on bubble transport process in Venturi bubble generator[J]. Atomic Energy Science and Technology, 2016, 50(6): 1034-1039. (in Chinese) |




