气动弹性振动由结构的惯性力弹性力和气动力耦合作用产生, 对工程结构是一种不利的现象, 一般需要通过控制加以避免和抑制[1].近年来, 气动弹性能量采集开始被学者们关注, 其核心思想是将结构气动弹性振动的机械能转化为电能输出, 实现对气动弹性现象的有效利用[2].从能量采集的角度看, 气动弹性现象是潜力能量源, 二者的结合具有一定优势.例如,自然风的存在使得气动弹性能量采集有很广泛的应用, 气动弹性现象的自激特性简化了能量采集装置的设计.此外, 气动弹性能量采集为小尺度风力发电提供了新的途径.能量采集技术的应用可以有效降低结构复杂程度, 提高系统可靠性可维护性, 降低维护成本和时间.通过能量采集收集的电能有潜力为电池充电,为低功耗系统供给能量, 甚至实现某些微小型电子系统的自我供给.由此观之, 气动弹性能量采集具有一定研究意义和价值.
作为一门跨学科领域, 气动弹性能量采集系统较为复杂, 其理论建模涉及结构换能器空气动力模型的相互耦合; 其中,气动模型对于系统的动力学响应以及能量输出的分析结果有着重要影响, 目前尚且缺少针对该部分内容的综述, 有必要进行系统地总结和讨论.从气动弹性机理来看, 现有能量采集方案包括基于翼段颤振非流线体驰振圆柱体尾涡诱导平板和机翼颤振的设计方案[3].本文针对不同类型的气动弹性能量采集, 分别对涉及的气动模型进行介绍, 讨论当前模型的不足与未来可发展方向.
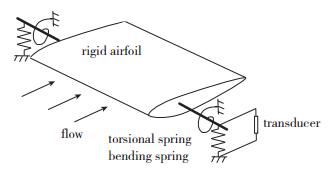
1 翼段能量采集系统气动建模翼段气动弹性能量采集设计利用了与机翼气动弹性颤振相同的机理, 颤振是机翼的惯性力弹性力与气动载荷耦合作用导致的剧烈自激振动.因为实际气动弹性系统中存在非线性因素, 结构可以在来流速度超过临界颤振速度后维持一定幅值的振动, 即极限环振动(limit cycle oscillation,LCO).为了采集LCO的机械能,能量采集装置包括刚性翼段提供翼段沉浮运动的弹性结构(通常为梁)提供翼段俯仰运动的铰链与扭转弹簧[4], 整体装置如图 1所示.当装置受到来流作用产生LCO时, 并联在其沉浮自由度的换能器能够实现能量的转换和输出.
|
| 图 1 翼段气动弹性能量采集示意图 Fig.1 Schematic of airfoil-based aeroelastic energy harvesting |
针对翼段气动弹性能量采集的气动建模, 自然地借鉴了二元机翼气动弹性分析使用的模型.从工程应用的角度来看, 具有一定准确性而又尽量简单的气动模型最为可取.目前在翼段气动弹性能量采集研究中应用最为广泛的是Theodorsen理论[5], 其假设气流为不可压无黏无旋流动, 给出翼段上气动载荷的线性二维解析形式.为了便于时域数值运算, 基于Theodorsen理论的积分形式气动升力L和力矩M分别为[6]
| $ \begin{align} & L\left( t \right)=-\pi \rho {{b}^{2}}\left[ U\dot{\theta }\left( t \right)+\dot{w}\left( t \right)-ba\ddot{\theta }\left( t \right) \right]- \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ 2\pi \rho Ub\left[ {{Q}_{3/4}}\left( 0 \right)\varphi \left( t \right)+\int_{0}^{t}{\frac{\rm{d}{{\mathit{Q}}_{\rm{3/4}}}\left( \tau \right)}{\rm{d}\tau }}\varphi \left( t-\tau \right)\rm{d}\tau \right], \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ M\left( t \right)=\pi \rho {{b}^{2}}\left[ ba\ddot{w}\left( t \right)-Ub\left( \frac{1}{2}-a \right)\dot{\theta }\left( t \right)-\left( \frac{1}{8}+{{a}^{2}} \right){{b}^{2}}\ddot{\theta }\left( t \right) \right]+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2\pi \rho U{{b}^{2}}\left( \frac{1}{2}+a \right)\left[ {{Q}_{3/4}}\left( 0 \right)\varphi \left( t \right)+\int_{0}^{t}{\frac{\rm{d}{{\mathit{Q}}_{\rm{3/4}}}\left( \tau \right)}{\rm{d}\tau }}\varphi \left( t-\tau \right)\rm{d}\tau \right]. \\ \end{align} $ |
其中,w为刚轴的沉浮变形, 向下为正; θ为刚轴扭转变形, 抬头为正; b为翼段半弦长; U为来流速度; a为翼段刚轴至半弦长位置的无量纲间距, 向后为正;
| $ {{Q}_{3/4}}\left( \tau \right)={{U}_{a}}\theta +\dot{w}+b\left( x \right)\left( 1/2-a \right)\dot{\theta }; $ |
ρ为空气密度; φ(t)为基于Jone's的Wagner近似函数
| $ \varphi \left( t \right)=1-{{A}_{1}}{{\rm{e}}^{-{{b}_{1}}\frac{U}{b}\cdot t}}-{{A}_{2}}{{\rm{e}}^{-{{b}_{2}}\frac{U}{b}\cdot t}}. $ |
其中, A1, A2, b1和b2为常值系数.
非定常涡格法(unsteady vortex lattice method,UVLM)是另一类较为常用的线性非定常气动模型, 同样假设不可压无黏无旋流动. UVLM通过计算翼段表面由于加速度以及环量产生的压力分布得到气动载荷, 因此能够考虑附加惯性力和尾流的影响[7].相比于Theodorsen理论, UVLM能够更好地分析翼弦方向非常规形状的翼段结构, 例如Abdelkefi等[8]基于UVLM数值研究了结构带有空腔的翼段的气动弹性能量采集. UVLM另一个优势在于, 能够考虑展向流动导致的三维效应, 因此对于中小展弦比的翼段结构更加适用.
对于翼段能量采集系统, 在其正常工作过程中, 可能产生较大振幅的振动, 翼段俯仰方向的大转角运动,很可能引起流动分离, 即失速现象.上述两类线性非定常气动模型无法考虑这种大迎角下的气动非线性(一般而言, 只适用于迎角小于8°的情况).为此, 一部分翼段能量采集系统的理论建模采用了半经验的失速模型[9], 其气动升力和力矩的准定常表达式为
| $ \left\{ \begin{align} & L=\frac{1}{2}\rho {{U}^{2}}b{{C}_{\rm{L}}}\left[{{\alpha }_{\rm{eff}}}\left( t \right)-{{C}_{\rm{S}}}\alpha _{\rm{eff}}^{3}\left( t \right) \right] \\ & D=\frac{1}{2}\rho {{U}^{2}}b{{C}_{\rm{D}}}\left[{{\alpha }_{\rm{eff}}}\left( t \right)-{{C}_{\rm{S}}}\alpha _{\rm{eff}}^{3}\left( t \right) \right] \\ \end{align} \right.. $ |
其中,CS为与动失速有关的非线性参数, 通过实验测量得到; CL和CD分别为升力和阻力系数; αeff为翼段瞬时运动有效攻角, 可以通过下式得到
| $ {{\alpha }_{\rm{eff}}}\left( t \right)=\theta \left( t \right)+\frac{\dot{w}\left( t \right)}{U}+b\left( \frac{1}{2}-a \right)\frac{\dot{\theta }\left( t \right)}{U}. $ |
准定常失速模型由于形式较为简单,便于后续对气动弹性系统进行非线性动力学近似解析分析.
总体而言, 大部分翼段气动弹性能量采集系统目前依然采用准定常非线性气动模型或非定常线性气动模型.由于准定常失速模型忽略了非定常效应, 因此难以准确求解失速情况下的气动载荷. Bryant等[10]在针对翼段气动弹性能量采集系统的建模中, 强调了动失速模型的必要性,如法国国家航天航空研究中心(Office National d′Etudes et de Recherches Aerospatiales,ONERA)的学者提出的半经验非定常ONERA动失速模型, 能够描述翼段亚颤振和过颤振状态下的气动载荷.不过,由于考虑动失速的气动模型均为半经验模型, 只适用于特定的翼型, 因此在使用上具有一定局限性.另外, 以ONERA模型为代表的二维动失速模型,较难研究中小展弦比结构的三维流动,其应用也受到了限制.综上可见, 翼段气动弹性能量采集系统的建模需要更为准确的三维非线性气动模型.
2 非流线体能量采集系统气动建模用于能量采集的非流线体气动弹性现象分为两类:一类是非流线体的气动弹性失稳, 称为驰振; 另一类是弹性结构在非流线体尾涡激励下产生的振动.下面分别对这两类气动弹性能量采集系统的气动建模研究进行介绍.
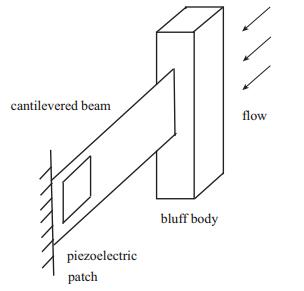
2.1 基于非流线体驰振的能量采集与翼段颤振类似, 当来流速度超过某一临界速度后, 具有特定截面形状的非流线体在来流中会沿垂直于来流方向产生单自由度振动, 这种现象被称为非流线体驰振.其产生机理为:当来流速度超过临界值时, 气流在非流线体表面形成剪切层, 产生内环量, 进而产生垂直于来流方向的压力, 该不平衡压力导致非流线体发生准静态的定幅值周期性运动[11].非流线体驰振的运动幅值比较大, 因此适合于能量采集.相应的能量采集装置一般使用沉浮支撑元件(如梁)固定非流线体, 换能器与非流线体的沉浮自由度并联, 如图 2所示.
|
| 图 2 非流线体驰振能量采集示意图 Fig.2 Schematic of energy harvesting based on the galloping oscillation of a bluff body |
非流线体的驰振是一种准定常振动, 其结构振动的时间尺度相比来流的时间尺度非常大.针对驰振动力学特性的研究证明:非流线体在来流作用下产生的气动载荷可以通过准定常假设得到.针对非流线体驰振的气动建模, 一般采用多项式形式来近似表示高Reynolds数下垂直来流方向的气动载荷[12], 如下式所示
| $ L=\frac{1}{2}\rho {{U}^{2}}S\left[{{\alpha }_{\rm{1}}}\frac{\dot{w}\left( t \right)}{U}-{{\alpha }_{\rm{3}}}{{\left( \frac{\dot{w}\left( t \right)}{U} \right)}^{3}} \right]. $ |
其中, S为特征面积, 对于非流线体即其截面面积; a1和a3为半经验常值系数, 前者代表气动力在零迎角下的斜率, 二者的值依赖于非流线体的展弦比与截面形状.
另外, 少部分非流线体气动弹性能量采集系统采用非定常气动建模, 如计算H型截面非流线体的气动弹性特性时, 通过铅垂以及转角方向的位移和速度组成气动升力和力矩的非线性函数[13].
总体而言, 绝大多数非流线体驰振能量采集研究中,气动建模均采用准定常假设.较少研究考虑在准定常假设的基础上构建非定常气动载荷, 以便能够考虑非流线体尾流的影响.未来研究中,可以考虑非定常气动载荷与现有气动模型的理论和实验结果对比.
2.2 基于圆柱体后缘涡的能量采集均匀来流中, 非流线体(一般考虑圆柱体)下缘会产生周期性的涡脱落, 即Kármán涡街, 进而在其自身上产生不平衡力.当涡脱落的频率与非流线体的固有振动频率接近时, 会发生共振, 使得非流线体在垂直与来流的方向上发生单自由度振动.基于这个原理实现能量采集的装置示意图与图 2所示的装置基本一致.
针对非流线体自激涡致振动的气动建模, 由于较为复杂, 因此相当一部分学者通过计算流体力学(CFD)方法进行研究[14].流体力学控制方程, 即Navier-Stokes方程, 是由流体质量动量和能量守恒推导得到的, 其表达式为
| $ \left\{ \begin{align} & \frac{\partial \rho }{\partial t}+\nabla \cdot \left( \rho \mathit{\boldsymbol{v}} \right)=0 \\ & \frac{\partial \left( \rho \mathit{\boldsymbol{v}} \right)}{\partial t}+\nabla \cdot \left( \rho \mathit{\boldsymbol{v}}\times \mathit{\boldsymbol{v}} \right)=\nabla \cdot \mathit{\boldsymbol{ }}\!\!\tau\!\!\rm{ }+\rho \mathit{\boldsymbol{f}} \\ & \frac{\partial \left( \rho \mathit{e} \right)}{\partial t}+\nabla \cdot \left( \rho e\mathit{\boldsymbol{v}} \right)=\rho \mathit{\boldsymbol{f}}\cdot \mathit{\boldsymbol{v}}\rm{-}\nabla \cdot \mathit{\boldsymbol{q+}}\nabla \cdot \left( \mathit{\boldsymbol{ }}\!\!\tau\!\!\rm{ }\cdot \mathit{\boldsymbol{v}} \right) \\ \end{align} \right.. $ | (1) |
其中,v为流体速度矢量; τ=-pI+τv为应力张量, 其中τv为黏性应力张量; p为流体压强; f为外力矢量; e为流体总能量; q为热通量矢量.式(1) 可以通过直接数值仿真的方式求解,但不适用于复杂几何外形情况下的应用;此时,可以使用Reynolds平均方法,为确保式(1) 中的系统封闭, 还需要基于流体介质输运特性本构关系以及状态方程(湍流模型)引入附加方程.
由于CFD方法运算量大, 计算效率低, 因此一些简化的气动模型也被设计并采用.针对圆柱体涡致自激振动, 其产生的垂直于来流的升力系数CL可以通过下式求解得到[15]:
| $ \begin{align} & \mathit{\ddot{C}}_{\rm{L}}^{2}+\omega _{\rm{s}}^{2}{{C}_{\rm{L}}}-\left[C_{\rm{L0}}^{2}-C_{\rm{L}}^{2}-{{\left( \frac{{{{\dot{C}}}_{\rm{L}}}}{{{\omega }_{\rm{s}}}} \right)}^{2}} \right]\times \\ & \left( {{\omega }_{\rm{s}}}G{{{\dot{C}}}_{\rm{L}}}-\omega _{\rm{s}}^{2}H{{C}_{\rm{L}}} \right)={{\omega }_{\rm{s}}}F\left[\frac{\dot{w}\left( t \right)}{D} \right]. \\ \end{align} $ |
其中,D为圆柱体直径; ωs为涡脱落的频率, 该频率取决于来流速度与Strouhal数; CL0,G,H和F均为系数, 取决于实验测量得到的无量纲阻尼与质量特性.
非流线体的尾涡还可以用来激励下游的柔性结构, 如悬臂梁.当尾涡引起的简谐激励频率与梁的固有频率接近时, 能够引发共振.若在梁上布置换能器, 则可以实现能量采集, 见图 3.该激励力的产生机理包含两个方面:尾涡流过梁表面形成的诱导流动冲击, 以及在梁另一个表面尾涡生成的低压区域[16].

|
| 图 3 圆柱体尾涡激励振动能量采集示意图 Fig.3 Schematic of energy harvesting based on the wake vortex excitation due to an upstream cylinder |
非流线体尾涡产生的周期载荷同样可以采用CFD方法得到.由于可以将这个周期载荷考虑为简谐力, 因此在初步设计时可以通过下式进行估算[17]:
| $ L=\frac{1}{2}\rho {{U}^{2}}\mathit{D}{{C}_{\rm{L}}}\sin \left( {{\omega }_{\rm{s}}}t \right). $ |
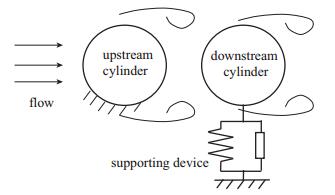
尾涡驰振现象发生于流动中沿流向两平行圆柱体之间,结合了非流线体驰振和尾涡诱导振动的特点.固定上游圆柱,当两个圆柱体的相对位置合适时,下游圆柱体可以产生较大振幅的横向振动[18],图 4给出了尾涡驰振能量采集的示意图.当前针对尾涡驰振,尚未有解析形式的气动载荷供理论和数值研究.
|
| 图 4 圆柱体尾涡驰振能量采集示意图 Fig.4 Schematic of energy harvesting based on the wake galloping phenomenon |
总体来说, 基于圆柱体后缘涡的气动弹性能量采集系统分析, 较多地使用了CFD手段.然而对于整个气动弹性能量采集领域, CFD并没有被广泛使用, 其主要原因依然在于CFD运算量过于庞大, 即相对于气动弹性能量采集应用来说计算花费过大.相比之下, 应用气动理论与工程模型显得比较高效.未来研究中为了提高CFD运算效率减少运算时间, 可以采用降阶模型等技术改善这一现状.
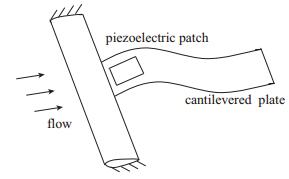
3 板或机翼能量采集系统气动建模悬臂平板或机翼结构在气流中自激产生LCO是典型的气动弹性失稳现象, 二者的机理都与机翼颤振一致.如图 5所示, 前缘固定后缘自由的柔性悬臂压电平板处于轴向均匀流动中, 当来流速度超过临界值时, 平板的LCO使压电换能器产生电能输出, 实现能量采集[19].类似地, 受到横向来流作用的悬臂平板也能够用于能量采集.
|
| 图 5 平板气动弹性能量采集示意图 Fig.5 Schematic of plate-based aeroelastic energy harvesting |
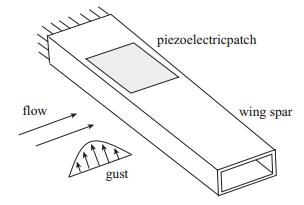
对于飞行器机翼, 可以将目标能量源着眼于大气紊流阵风等扰动导致的气动弹性响应[20]. 图 6给出了一种基于机翼的能量采集方案[6], 如图所示, 压电片粘接于机翼翼盒的上下表面, 当机翼受到离散阵风的扰动时, 机翼将产生阵风响应,此时换能器产生一定量的电压输出.
|
| 图 6 机翼气动弹性响应能量采集示意图 Fig.6 Schematic of wing-based aeroelastic energy harvesting from the gust excitation |
对于平板或机翼气动弹性能量采集系统, 其气动模型研究可以借鉴翼段能量采集系统.三维非定常涡格法是常用的线性非定常气动载荷的求解方法[21].此外,二维气动模型, 如Theodorsen理论, 可以和片条理论结合使用, 将沿展向各个截面的气动载荷通过升力线模型组合起来, 近似分析三维机翼[22].另外, 前缘固定的悬臂平板的气动弹性分析中, CFD技术也得到了较为广泛的应用.由于结构的柔性或机翼的大展弦比构型, 平板或机翼同样很可能产生大挠度和大转角, 尤其在其自由端位置最为严重, 此时, 同样需要考虑大迎角下的气动非线性, 气动建模应考虑三维非线性模型.
4 结论本文主要对当前气动弹性能量采集分析中的气动建模进行了综述.针对不同类型的气动弹性能量采集系统, 分别对气动模型进行了总结和讨论.基于翼段柔性平板和机翼的气动弹性能量采集研究中, 气动模型目前广泛使用的依然是线性非定常气动模型, 能够较便捷快速地完成分析,但不能较好地计算结构大振幅下的振动, 很可能导致估算的电能输出偏高, 准定常和非定常失速模型的应用弥补了这一缺点,前者还便于非线性动力学近似解析分析,但由于它们都是半经验的二维模型,也具有一定局限性,因此,在未来研究中应考虑使用三维非线性气动模型.另一方面, 非流线体驰振能量采集系统气动模型的研究广泛应用准定常假设, 后续研究中可以考虑构建非定常模型, 与准定常模型实现对比; 圆柱体涡致振动能量采集的研究中则相对较多地应用了CFD技术计算气动载荷.对于上述各类气动弹性能量采集系统, 未来工作都可以考虑使用更加高效的CFD手段, 对现有模型进行验证.
| [1] |
Lee B H, Price S J, Wong Y S. Nonlinear aeroelastic analysis of airfoils: bifurcation and chaos[J]. Progress in Aerospace Sciences, 1999, 35(3): 205-334. DOI:10.1016/S0376-0421(98)00015-3 |
| [2] |
Truitt A, Mahmoodi S N. A review on active wind energy harvesting designs[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(9): 1667-1675. DOI:10.1007/s12541-013-0226-4 |
| [3] |
吴沂宁, 李道春, 向锦武. 基于气动弹性振动的能量采集[A]. //第十四届全国空气弹性学术交流会会议[C]. 西安, 2015. Wu Y N, Li D C, Xiang J W. Energy harvesting based on aeroelastic vibrations[A]. //14th National Academic Conference on Aeroelasticity[C]. Xi'an, 2015(in Chinese). |
| [4] |
Wu Y, Li D, Xiang J. Performance analysis and parametric design of an airfoil-based piezoaeroelastic energy harvester[A]. //56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference[C]. Kissimmee, 2015.
|
| [5] |
Erturk A, Vieira W G, Marqui C, et al. On the energy harvesting potential of piezoaeroelastic systems[J]. Applied Physics Letters, 2010, 96(18): 184103. DOI:10.1063/1.3427405 |
| [6] |
Xiang J, Wu Y, Li D. Energy harvesting from the discrete gust response of a piezoaeroelastic wing: modeling and performance evaluation[J]. Journal of Sound and Vibration, 2015, 343: 176-193. |
| [7] |
Abdelkefi A, Ghommem M, Nuhait A O, et al. Nonlinear analysis and enhancement of wing-based piezoaeroelastic energy harvesters[J]. Journal of Sound and Vibration, 2014, 333(1): 166-177. DOI:10.1016/j.jsv.2013.08.032 |
| [8] |
Abdelkefi A, Nuhait A O. Modeling and performance analysis of cambered wing-based piezoaeroelastic energy harvesters[J]. Smart Materials and Structures, 2013, 22(9): 095029. DOI:10.1088/0964-1726/22/9/095029 |
| [9] |
Abdelkefi A, Nayfeh A H, Hajj M R. Design of piezoaeroelastic energy harvesters[J]. Nonlinear Dynamics, 2012, 68(4): 519-530. DOI:10.1007/s11071-011-0233-x |
| [10] |
Bryant M, Garcia E. Modeling and testing of a novel aeroelastic flutter energy harvester[J]. Journal of Vibration and Acoustics, 2011, 133(1): 011010. DOI:10.1115/1.4002788 |
| [11] |
Bibo A, Alhadidi A H, Daqaq M F. Exploiting a nonlinear restoring force to improve the performance of flow energy harvesters[J]. Journal of Applied Physics, 2015, 117(4): 045103. DOI:10.1063/1.4906463 |
| [12] |
Dai H L, Abdelkefi A, Javed U, et al. Modeling and performance of electromagnetic energy harvesting from galloping oscillations[J]. Smart Materials and Structures, 2015, 24(4): 045012. DOI:10.1088/0964-1726/24/4/045012 |
| [13] |
Zhu J, Zhang W. Coupled analysis of multi-impact energy harvesting from low-frequency wind induced vibrations[J]. Smart Materials and Structures, 2015, 24(4): 045007. DOI:10.1088/0964-1726/24/4/045007 |
| [14] |
Mehmood A, Abdelkefi A, Hajj M R, et al. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder[J]. Journal of Sound and Vibration, 2013, 332(19): 4656-4667. DOI:10.1016/j.jsv.2013.03.033 |
| [15] |
Abdelkefi A, Hajj M R, Nayfeh A H. Phenomena and modeling of piezoelectric energy harvesting from freely oscillating cylinders[J]. Nonlinear Dynamics, 2012, 70(2): 1377-1388. DOI:10.1007/s11071-012-0540-x |
| [16] |
Akaydın H D, Elvin N, Andreopoulos Y. Wake of a cylinder:a paradigm for energy harvesting with piezoelectric materials[J]. Experiments in Fluids, 2010, 49(1): 291-304. DOI:10.1007/s00348-010-0871-7 |
| [17] |
Nayyar A, Stoilov V. Power generation from airflow induced vibrations[J]. Wind Engineering, 2015, 39(2): 175-182. DOI:10.1260/0309-524X.39.2.175 |
| [18] |
Jung H J, Lee S W. The experimental validation of a new energy harvesting system based on the wake galloping phenomenon[J]. Smart Materials and Structures, 2011, 20(5): 055022. DOI:10.1088/0964-1726/20/5/055022 |
| [19] |
Tang L, Païdoussis M P, Jiang J. Cantilevered flexible plates in axial flow:energy transfer and the concept of flutter-mill[J]. Journal of Sound and Vibration, 2009, 326(1/2): 263-276. |
| [20] |
Anton S R, Erturk A, Inman D J. Multifunctional self-charging structures using piezoceramics and thin-film batteries[J]. Smart Materials and Structures, 2010, 19(11): 115021. DOI:10.1088/0964-1726/19/11/115021 |
| [21] |
Dunnmon J A, Stanton S C, Mann B P, et al. Power extraction from aeroelastic limit cycle oscillations[J]. Journal of Fluids and Structures, 2011, 27(8): 1182-1198. DOI:10.1016/j.jfluidstructs.2011.02.003 |
| [22] |
Wu Y, Li D, Xiang J. Design and analysis of energy harvester based on aeroelastic vibration[A]. //The 9th International Conference on Vibration Engineering and Technology of Machinery[C]. Nanjing, 2013.
|



