2. 国家计算流体力学实验室, 北京 100191
2. National Laboratory for Computational Fluid Dynamics, Beijing 100191, China
Boltzmann方程[1]是描述气体分子运动状态和运动规律的确定论基本方程, 主要描述单原子气体或简单气体的分子输运特性. 不考虑外力场影响的Boltzmann方程如公式(1)所示
| $ \frac{{\partial f}}{{\partial t}} + \mathit{\boldsymbol{\xi }} \cdot \frac{{\partial f}}{{\partial \mathit{\boldsymbol{r}}}} = \int\limits_{{R_3}} {\int_0^{{\rm{4 \mathsf{ π} }}} {\left( {{f^*}f_1^* - f{f_1}} \right){\xi _{\rm{r}}}\sigma {\rm{d}}\varOmega {\rm{d}}{\mathit{\boldsymbol{\xi }}_1}} } $ | (1) |
其中, f为气体分子的速度分布函数;t,r,ξ分别为时间、位置空间坐标、分子速度;ξr为碰撞分子的相对运动速度;σ为微分碰撞截面, 与分子之间的作用力模型相关;Ω为两个分子碰撞后相对速度的方向;R3表示ξ1的三维速度空间积分.
Boltzmann方程通过对气体分子速度分布函数矩积分得到流动的宏观参数, 可描述从稀薄流到连续流跨流域气体流动由非平衡态向平衡态演化的过程[2]. 然而, 直接采用理论分析或数值方法研究Boltzmann方程很难实现, 困难在于[3-4]: (1) 几率密度分布函数f具有至少7个自变量, 维度太高; (2) 碰撞项高度非线性, 且具有高维积分特点, 并与分子碰撞模型相关, 极其复杂. 虽然Aqarwal等[5]、Kolobov等[6]在求解Boltzmann方程或广义Boltzmann方程(generalized Boltzmann equation,GBE)方面取得了一些进展, 但也并未实现对碰撞项的直接求解, 并且由于求解过程复杂, 计算代价很大, 导致很难应用到工程中.
正是由于Boltzmann方程具有高维度、复杂碰撞积分项的特点, 对于跨流域非定常问题, 特别是稀薄过渡区的低速非定常流动, 其数值求解应该考虑基于Boltzmann的运动模型方程[7-12]. 近年, Polikarpov等[8]通过求解非定常Shakhov模型方程得到了气流穿过方形切口的瞬态流动, 并说明定常流场建立的时间与背压压比和气体稀薄度相关. Lihna-ropoulos等[9]通过数值求解时间依赖的BGK运动方程分析了圆柱管道中的气体启动过程. Chigullapalli等[7]求解Boltzmann-ESBGK模型方程发展了一种三维非定常稀薄流动求解器. 实践表明, 基于Boltzmann模型方程的数值求解方法是模拟稀薄流到连续流跨流域非定常流动的有效手段.
为了求解Boltzmann模型方程以得到跨流域数值模拟方法, 李志辉等在速度空间采用离散速度坐标法, 位置空间应用计算流体力学有限差分方法, 建立起从稀薄流到连续流的跨流域气体动理论统一算法(gas-kinetic unified algarithm, GKUA)[13-14], 并在定常流动研究中得到了较好的应用[15-16]. 实际上, 统一算法的求解过程是通过长时间非定常输运模拟得到最终的定常流动状态, 因此可通过技术改进得到整个非定常气体流动演化过程. 前期已分析了一维、二维跨流域非定常流动特征与稀薄效应对非定常流场影响机制[17], 并用于求解分析稀薄平面喷流扩散进入真空环境的非定常过程[18]. 结果表明, 基于GKUA的非定常流动求解器对于高真空自由分子流、稀薄流、过渡流等流区的超声速非定常流动具有较好适用性. 因此, 本文对连续流区的经典Karman涡街问题进行模拟, 以确认该跨流域非定常流动模拟算法对于连续流区低速流动的适应性.
1 控制方程及计算方法 1.1 控制方程GKUA能够求解各种模型方程[19], 包括BGK[20], ES-BGK[21],Shakhov [22]或者其他模型. 对于氮气或者空气, 室温状态下分子的转动能就已完全激发[23], 因此采用考虑转动自由度影响的双原子气体动理论模型方程能够更好地描述氮气流动. 此外, 众多学者已经对高温条件下多原子气体分子的振动能开展了有意义的分子动力学建模分析和数值计算工作[24-27], 后续如果研究高速、高温气体动力学问题时应该加以考虑.
基于对转动自由度松弛变化特性的Rykov模型研究[28-30], 采用转动惯量描述气体分子的自旋运动, 将分子总角动量守恒作为一个碰撞不变量, 在求解Boltzmann模型方程的统一算法理论框架[13-16]下, 构建考虑转动非平衡效应的Boltzmann模型方程
| $ {\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {f_0}}}{{\partial t}} + {\xi _i}\frac{{\partial {f_0}}}{{\partial {x_i}}} = {\nu _{\rm{r}}}\left( {f_0^{\rm{r}} - {f_0}} \right) + {\nu _{\rm{t}}}\left( {f_0^{\rm{t}} - {f_0}} \right)}\\ {\frac{{\partial {f_1}}}{{\partial t}} + {\xi _i}\frac{{\partial {f_1}}}{{\partial {x_i}}} = {\nu _{\rm{r}}}\left( {f_1^{\rm{r}} - {f_1}} \right) + {\nu _{\rm{t}}}\left( {f_1^{\rm{t}} - {f_1}} \right)} \end{array}} \right.} $ | (2) |
| $ {\nu _{\rm{r}}} = \frac{{{P_{\rm{t}}}}}{{{\mu _{\rm{t}}}}}\frac{1}{Z},{\nu _{\rm{t}}} = \frac{{{P_{\rm{t}}}}}{{{\mu _{\rm{t}}}}}\left( {1 - \frac{1}{Z}} \right) $ |
| $ \begin{array}{l} f_0^{\rm{r}} = n{\left( {\frac{m}{{2{\rm{ \mathsf{ π} }}kT}}} \right)^{3/2}}\exp \left( { - \frac{{m{c^2}}}{{2kT}}} \right) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {1 - \frac{2}{{15}}{\omega _0}\frac{{q_i^{\rm{t}}}}{P}\frac{{m{c_i}}}{{kT}}\left( {\frac{5}{2} - \frac{{m{c^2}}}{{2kT}}} \right)} \right] \end{array} $ |
| $ \begin{array}{l} f_0^{\rm{t}} = n{\left( {\frac{m}{{2{\rm{ \mathsf{ π} }}k{T_{\rm{t}}}}}} \right)^{3/2}}\exp \left( { - \frac{{m{c^2}}}{{2k{T_{\rm{t}}}}}} \right) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {1 - \frac{2}{{15}}\frac{{q_i^{\rm{t}}}}{{{P_{\rm{t}}}}}\frac{{m{c_i}}}{{k{T_{\rm{t}}}}}\left( {\frac{5}{2} - \frac{{m{c^2}}}{{2k{T_{\rm{t}}}}}} \right)} \right] \end{array} $ |
| $ \begin{array}{l} f_1^{\rm{r}} = nkT{\left( {\frac{m}{{2{\rm{ \mathsf{ π} }}kT}}} \right)^{3/2}}\exp \left( { - \frac{{m{c^2}}}{{2kT}}} \right) \cdot [1 - \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{2}{{15}}{\omega _0}\frac{{q_i^{\rm{t}}}}{P}\frac{{m{c_i}}}{{kT}}\left( {\frac{5}{2} - \frac{{m{c^2}}}{{2kT}}} \right) + {\omega _1}(1 - \delta )\frac{{q_i^{\rm{r}}m{c_i}}}{{PkT}}} \right] \end{array} $ |
| $ \begin{array}{l} f_1^{\rm{t}} = \varepsilon n{\left( {\frac{m}{{2{\rm{ \mathsf{ π} }}k{T_{\rm{t}}}}}} \right)^{3/2}}\exp \left( { - \frac{{m{c^2}}}{{2k{T_{\rm{t}}}}}} \right) \cdot [1 - \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{2}{{15}}\frac{{q_i^{\rm{t}}}}{{{P_{\rm{t}}}}}\frac{{m{c_i}}}{{k{T_{\rm{t}}}}}\left( {\frac{5}{2} - \frac{{m{c^2}}}{{2k{T_{\rm{t}}}}}} \right) + (1 - \delta )\frac{{q_i^{\rm{r}}m{c_i}}}{{\varepsilon nk{T_{\rm{t}}}}}} \right] \end{array} $ |
式中, 下标i表示空间维度方向; 角标t,r分别表示弹性碰撞和非弹性碰撞, 如νt和νr是弹性碰撞频率和非弹性碰撞频率; μ为黏性系数; Z为非弹性碰撞松弛因子;xi为位置空间坐标;ξi为气体分子速度分量;c为气体分子热运动速度;n,T,P分别为气体分子数密度、气体流动温度和压力;k为Boltzmann常数;m为分子质量;δ对于分子间相互作用规律来说是一个常数δ=μt/(mnD), D是自扩散系数.
物理空间宏观流动参数可以由f0和f1在速度空间上积分[13, 28]求得
| $ {n = \int {{f_0}} {\rm{d}}\mathit{\boldsymbol{\xi }},n{U_i} = \int {{\xi _i}} {f_0}{\rm{d}}\mathit{\boldsymbol{\xi }}} $ |
| $ {\frac{3}{2}k{T_{\rm{t}}} = \frac{1}{n}\int {\frac{{m{c^2}}}{2}} {f_0}{\rm{d}}\mathit{\boldsymbol{\xi }},\quad q_i^{\rm{t}} = \int {{c_i}} \frac{{m{c^2}}}{2}{f_0}{\rm{d}}\mathit{\boldsymbol{\xi }}} $ |
| $ {\varepsilon = \frac{1}{n}\int {{f_1}} {\rm{d}}\mathit{\boldsymbol{\xi }},q_i^{\rm{r}} = \int {{c_i}} {f_1}{\rm{d}}\mathit{\boldsymbol{\xi }},\frac{5}{2}kT = \frac{3}{2}k{T_{\rm{t}}} + \varepsilon } $ |
| $ {k{T_{\rm{r}}} = \varepsilon ,{P_{\rm{t}}} = nk{T_{\rm{t}}},P = nkT} $ |
黏性系数μ和非弹性碰撞松弛因子Z可定义为如下的形式[29-30]
| $ {{\mu _{\rm{t}}} = \mu \left( {{T_{\rm{t}}}} \right) = \mu \left( {{T_*}} \right){t^{2/3}}/\varphi (t),t = {T_{\rm{t}}}/{T_*}} $ |
| $ {\varphi (t) = 0.767 + 0.233{t^{ - 1/6}}\exp [ - 1.17(t - 1)]} $ |
| $ \begin{array}{l} Z\left( {{T_{\rm{t}}},{T_{\rm{r}}}} \right) = \frac{3}{4}{\rm{ \mathsf{ π} }}\frac{{\varphi (t)}}{{{t^{1/6}}}}\frac{{9t}}{{t + 8}}\left( {\frac{{{T_{\rm{r}}}}}{{{T_{\rm{t}}}}}} \right)[0.461 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {0.5581\left( {\frac{{{T_{\rm{r}}}}}{{{T_{\rm{t}}}}}} \right) + 0.0358{{\left( {\frac{{{T_{\rm{r}}}}}{{{T_{\rm{t}}}}}} \right)}^2}} \right] \end{array} $ |
对于氮气N2而言, T*=91.5 K, δ=1/1.55.
1.2 无量纲化和速度空间的离散采用气体动理论数值计算方法可直接捕捉速度分布函数随时间的演化. 空间坐标、时间、数密度、流动速度、温度、黏性的无量纲参考量为[13-16]
| $ {L,L/\sqrt {2R{T_\infty }} ,{n_\infty },\sqrt {2R{T_\infty }} } $ |
| $ {{T_\infty },\frac{5}{{16}}m{n_\infty }\sqrt {2{\rm{ \mathsf{ π} }}R{T_\infty }} {\lambda _\infty }} $ |
而能量(包括平动能和转动能)的无量纲参考量以及分布函数f0和f1的无量纲参考量分别为
| $ {m{n_\infty }{{\left( {2R{T_\infty }} \right)}^{3/2}},{n_\infty }{{\left( {2R{T_\infty }} \right)}^{ - 3/2}}} $ |
| $ {m{n_\infty }R{T_\infty }{{\left( {2R{T_\infty }} \right)}^{ - 3/2}}} $ |
其中, λ∞为来流未扰动区域的分子平均自由程, 来流气体分子最可几热运动速度Cm∞作为特征速度: Cm∞=
对于二维流动, 为了对速度空间进行降维处理, 在对速度分布函数方程(2)应用离散速度坐标法之前, 需要引入3个约化速度分布函数, 对模型方程和基于速度空间的宏观流动矩积分进行约化处理, 这样可以减少对计算机内存的需求, 提高计算效率.
| $ {{g_1} = \int_{ - \infty }^{ + \infty } {{f_0}} {\rm{d}}{\xi _z},{g_2} = \int_{ - \infty }^{ + \infty } {\xi _z^2} {f_0}{\rm{d}}{\xi _z}} $ |
| $ {{g_3} = \int_{ - \infty }^{ + \infty } {{f_1}} {\rm{d}}{\xi _z}} $ |
得到关于二维约化速度分布函数gi(t, x, y, ξx, ξy), i=1, 2, 3的方程. 在此基础上, 使用离散速度坐标法对速度分量ξx,ξy进行数值离散.
应用离散速度坐标方法将物理空间的坐标(x, y)转换到计算平面(ζ, η), 模型方程转化成为每个离散速度坐标点上包含非线性源项的双曲型守恒方程
| $ \frac{{\partial \varPhi }}{{\partial t}} + \frac{{\partial F}}{{\partial \zeta }} + \frac{{\partial E}}{{\partial \eta }} = S $ | (3) |
其中,Φ=J[g1σ, ε, g2σ, ε, g3σ, ε]T, F=U·Φ, E=V·Φ, S=J·S. giσ, ε=giσ, ε(t, x, y), σ=1, 2,…,N1, ε=1, 2,…,N2, N1和N2分别为速度空间坐标ξx和ξy的离散点数. J为Jacobi变换矩阵, J=∂(x, y)/∂(ζ, η).
| $ {\bar U = {\zeta _x} \cdot {\xi _{x\sigma }} + {\zeta _y} \cdot {\xi _{y\varepsilon }}} $ |
| $ {\bar V = {\eta _x} \cdot {\xi _{x\sigma }} + {\eta _y} \cdot {\xi _{y\varepsilon }}} $ |
在离散速度坐标法中, 采用合适的积分规则对分布函数在速度空间进行矩积分, 其中积分所依赖的分布函数仅在某些离散速度坐标点上有确定值. 对分布函数在全速度域上的积分可基于这些离散速度点上的分布函数值得到. 求解方式是采用Gauss-Hermite数值积分法, 将全域积分转变为基于权重因子的求和. 基于此, 构造某些自适应选取的离散速度坐标点(ξxσ, ξyε), 以及对速度空间这些点上的分布函数值进行合理迭代求解至关重要, 这将直接影响数值模拟算法的收敛性和适用性. 值得注意的是, 这些离散速度坐标点确定的速度分布函数值必须保持正定性.
1.3 适于非定常流动计算的差分方法对于非定常流场的数值计算, 除了差分格式须满足耗散控制、色散控制和激波控制条件以保证计算过程中的稳定性、不产生虚假波动以及良好地捕捉激波外, 还应特别满足保频谱原则, 并且要求计算网格和边界计算方法要与内点计算匹配协调[31-32]. 一般采用固定时间步长的方法进行显式的时间推进, 但时间步长必须满足流场计算的格式稳定性条件.
基于非定常时间分裂方法[4, 13-16, 19]将控制方程(3)分裂成为包含非线性源项的碰撞松弛方程和计算平面(ζ, η)上的对流运动方程. 采用3阶WENO格式[19, 33]离散速度分布函数方程的对流项. 源项的碰撞松弛积分采用3阶Runge-Kutta方法求解. 考虑到在真实气体流动中对流运动和碰撞松弛具有相似的过程, 在数值计算中需要前向时间步长和后向时间步长的耦合迭代. 基于此, 在时间推进上采用基于非定常时间分裂法的3阶显式Runge-Kutta[34]时间推进, 得到在各个离散速度坐标点处数值求解约化速度分布函数方程的气体运动论耦合迭代数值格式
| $ {\varPhi ^{n + 1}} = {L_{\rm{s}}}\left( {\frac{{\Delta t}}{2}} \right){L_\eta }\left( {\frac{{\Delta t}}{2}} \right){L_\zeta }(\Delta t){L_\eta }\left( {\frac{{\Delta t}}{2}} \right){L_{\rm{s}}}\left( {\frac{{\Delta t}}{2}} \right){\varPhi ^n} $ | (4) |
其中, 下标s表示源项, ζ, η为计算平面坐标. (4)式表示在Δt时间步长之后的分布函数值通过半时间步长(Δt/2)的两次松弛演化得到, 这样可以提高该差分离散格式的时间精度.
方程(4)的每一项对应于非线性方程(3)的数值计算, 其中Ls, Lη和Lζ分别表示碰撞松弛源项以及两个计算平面坐标方向的对流运动项的差分方程.
| $ {\frac{{\partial \varPhi }}{{\partial t}} = S} $ |
| $ {\frac{{\partial \varPhi }}{{\partial t}} + \frac{{\partial E}}{{\partial \eta }} = 0} $ |
| $ {\frac{{\partial \varPhi }}{{\partial t}} + \frac{{\partial F}}{{\partial \zeta }} = 0} $ |
引入3阶WENO格式[35]对计算平面进行扫描. 对于时间项, 可以使用Runge-Kutta法(RK-3)来提高精度.
| $ {{\varPhi ^{(1)}} = {\varPhi ^{(n)}} + \Delta t \cdot L\left( {{\varPhi ^{(n)}}} \right)} $ |
| $ {{\varPhi ^{(2)}} = \frac{3}{4}{\varPhi ^{(n)}} + \frac{1}{4}{\varPhi ^{(1)}} + \frac{1}{4}\Delta t \cdot L\left( {{\varPhi ^{(1)}}} \right)} $ |
| $ {{\varPhi ^{(n + 1)}} = \frac{1}{3}{\varPhi ^{(n)}} + \frac{2}{3}{\varPhi ^{(2)}} + \frac{2}{3}\Delta t \cdot L\left( {{\varPhi ^{(2)}}} \right)} $ |
数值计算过程中的时间步长Δt由格式稳定条件约束
| $ \Delta t = {\rm{CFL}}/\max \left( {\frac{{{\nu _{\rm{r}}} + {\nu _{\rm{t}}}}}{2},\frac{{|\bar U|}}{{\Delta \zeta }},\frac{{|\bar V|}}{{\Delta \eta }}} \right) $ |
其中, CFL为时间步长调节系数, 一般CFL < 1.
2 Karman涡街形成及运动的数值模拟 2.1 问题描述一定条件下的定常来流绕过钝体时, 物体两侧可能会周期性地脱离出旋转方向相反、排列规则的双列线涡, 经过非线性作用后会形成Karman涡街. 以圆柱绕流为例, 低Reynolds数时圆柱后方有一对尾涡; 随着Re的增加, 尾迹出现震荡; 继续增加Re, 近尾迹中涡交替脱落, 进入下游, 形成持续较长距离的稳定涡列, 即Karman涡街[36]. 本文选取Re=1 200时作为典型计算条件, 对应的计算状态如表 1所示, 气体为氮气.
| 下载CSV 表 1 低速Karman涡街算例的典型计算状态 Tab.1 Classical computing condition for low-speed Karman vortex street case |
圆柱直径d=1 m, 数值计算过程中流场网格关于x轴对称(如图 1所示), 物理空间的网格量为(301×201), 分子速度空间的离散速度点为(16×16), 关于速度空间的矩积分采用Gauss-Hermite积分法. 圆柱尾迹区Karman涡街的形成、发展、运动及耗散过程如图 2所示, 图中给出的是不同时刻流场压力等值线云图. 初始时刻流场完全处于来流状态, 壁面扰动从t=0时刻开始传播. 对于低速流动, 扰动向全流场传播. 在图 2(a)所示的t=0.014 s时刻, 物面边界扰动已经传播到离圆柱较远的距离, 圆柱周围流场基本成形. 此时能够明显看到圆柱头部区域的高压、圆柱上下两侧的低压以及圆柱后方的扰动区都是上下对称的. 到图 2(b)所示的t=0.024 s时刻, 圆柱后端尾迹区出现了上下对称的两个低压旋涡结构. 可以看到, 低压旋涡结构的产生是由逆压梯度导致的流动分离. 分离出的旋涡持续向下游流动, 并逐渐发展、扩大. 到图 2(c)所示的t=0.057 s时刻, 尾迹区两个涡在向下游流动的同时相互接触、互相影响, 但此时两个旋涡依然是对称结构. 而在图 2(d)的t=0.569 s时刻, 尾迹区两个旋涡结构“对称破缺”, 上下两个涡交替“扩大—收缩”, 并继续向下游流动. 这种对称性被打破的现象来源于流场的非稳态演化, 与外界干扰、网格结构等并无关系. 随着旋涡结构的持续运动、发展、相互作用, 到图 2(e)的t=0.687 s时刻形成了“拟序结构”的尾迹区旋涡序列, 并最终形成了图 2(f), (g)所示“Karman涡街”非定常流动状态. 其中, 图 2(f)和(g)分别是半个周期的Karman涡街运动耗散过程, 旋涡结构呈现上下交替演化现象, 从图中可以看到Karman涡街脱落、发展、运动、耗散的整个过程.

|
| 图 1 低速圆柱绕流的物理空间网格 Fig.1 Grid system in physical space for low-speed flow past a cylinder |

|
| 图 2 低速圆柱绕流不同时刻的压力等值线云图 Fig.2 Pressure contours of low-speed flow past a cylinder at different time |
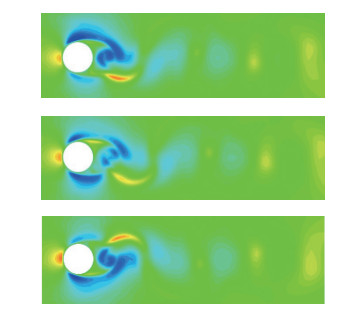
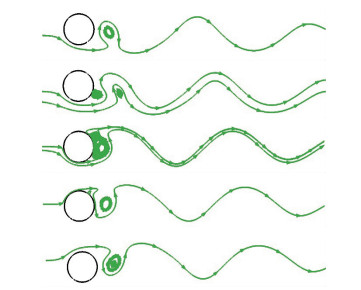
图 3给出了圆柱绕流尾迹区在半个周期内的Karman涡街交替脱落现象. 从流场的温度等值线云图中能够更明显地看到圆柱上下顶点稍靠后的位置交替“甩出”涡旋结构, 及其涡脱离的整个过程. 有意思的是, 甩出的涡旋结构为低压、低温, 而另一侧对应被压缩的区域则是高压、高温. 产生的Karman涡街在离圆柱尾部4d距离以后逐渐被耗散掉. 图 4详细绘出了半个周期内的流线图, 展示了圆柱尾迹区下半部甩出旋涡到上半部甩出旋涡的交替演化过程.
|
| 图 3 圆柱绕流尾迹区半个周期内的Karman涡街交替脱落现象(温度) Fig.3 Alternately dropping phenomenon of the Karman vortex street in half period at the wake-region of flow past a cylinder(temperature contours) |
|
| 图 4 圆柱绕流尾迹区半个周期内的流线图 Fig.4 Streamlines in half period at the wake-region of flow past a cylinder |
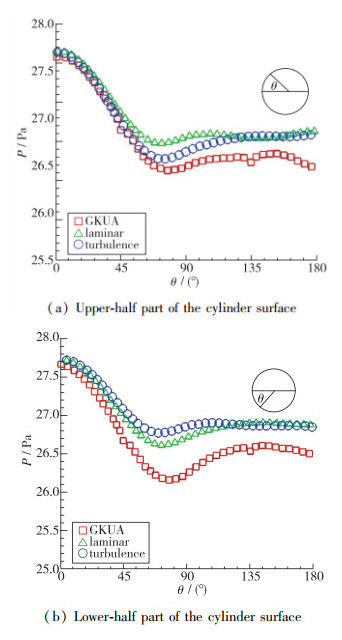
图 5给出了本文GKUA得到圆柱上下表面的压力分布与连续流区N-S方程数值计算结果的比较, 其中N-S方程计算中分别采用了层流模型和两方程k-ε湍流模型(RANS). 可以看到, GKUA得到的表面压力分布规律与连续流区经典N-S方程基本一致. 对于该低速流动, 迎风面压力值略高于背风区, 且GKUA得到的迎风面压力分布与层流模型和湍流模型都吻合较好. 背风面压力值的差别相对来说要大一些, 但也在可控范围内(最大偏差低于2.3%). 同时可以看出, 上下表面压力分布的不对称性正体现出了流动的非定常特性, 这跟尾迹区涡的交替脱落紧密相关.
|
| 图 5 圆柱上下表面压力比较 Fig.5 Comparison of pressures on the cylinder surface |
分析圆柱绕流尾迹区Karman涡街的演化规律能够测算出该状态下Karman涡街的周期Tp≈0.087 66. 表征Karman涡街非定常运动的Strouhal数(Sr)与旋涡发射频率
| $ {S_{\rm{r}}} = \frac{{\bar \omega d}}{{\bar v}} = \frac{d}{{{T_{\rm{p}}}\bar v}} $ |
其中, 旋涡发射频率
该状态下圆柱绕流数值计算得到的Strouhal数与文献[37]中的实验值比较如表 2所示. 可以看到, 本文数值计算得到的表征Karman涡街非定常流动特征的Strouhal数与实验值和公认理论值0.21都是非常接近的. 考虑到数据量的问题, 在数值计算过程中并没有保存任意时刻的流场结果, 而是隔一定时间保存一次, 导致Karman涡街的周期估算值存在一定偏差. 鉴于此, 本次圆柱绕流尾迹区Karman涡街的数值模拟结果是可信的.
| 下载CSV 表 2 圆柱绕流计算得到的Strouhal数与文献比较 Tab.2 Comparison of the Strouhal numbers from simulation and experiment |
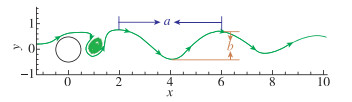
Karman涡街的尺寸比定义为b/a, 该参数可以用来描述涡列, 其中a为同涡列中相邻旋涡之间的距离, b为两列旋涡的间隔(见图 6). von Karman[38]给出涡列稳定的必要条件为尺寸比b/a≈0.281. 虽然后人指出Karman涡街稳定的尺寸比并不严格等于0.281[39], 但不同计算条件下相差不多. 本文数值计算圆柱Karman涡街的尺寸比b/a=0.283, 与von Karman理论推导的结果非常接近(见表 3), 进一步验证了气体动理论统一算法模拟Karman涡街等非定常流动问题是适用的.
|
| 图 6 Karman涡街尺寸比示意图 Fig.6 Sketch of the length ratios for Karman vortex street |
| 下载CSV 表 3 圆柱Karman涡街尺寸比的计算值与理论值比较 Tab.3 Comparison of the length ratios from simulation and theory analysis |
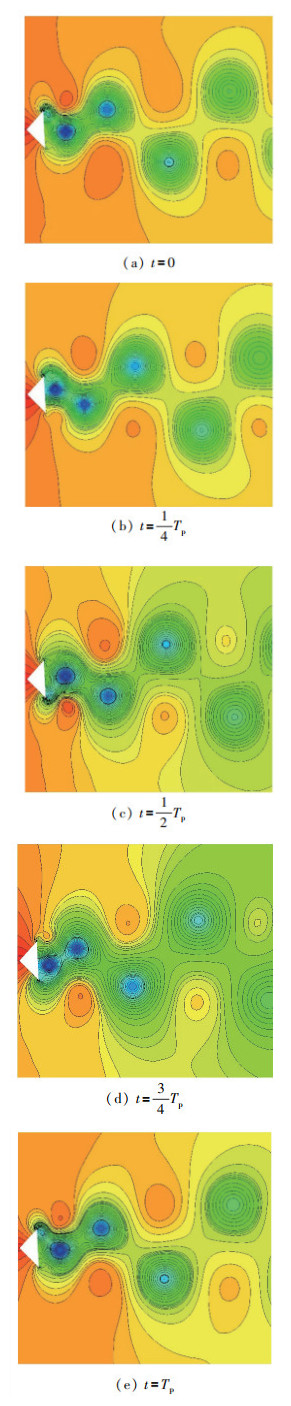
圆柱绕流的Karman涡街是由流动的对称性破缺引起的, 而非对称尖劈绕流则由于流场本身的非对称性, 诱导产生的Karman涡街在空间上是非对称的, 但在时间上呈现出周期变化的规律. 非对称尖劈的物理空间流场网格如图 7所示, 规模为58 403个网格点, 分子速度空间采用(32×32)的Gauss-Hermite积分法. 图 8给出了一个周期内非对称尖劈诱导涡街的流场压力等值线云图, 其中t=0表示该周期的起始时刻, 并不是初始时刻. 可以看到, 上下尖劈诱导产生的涡系结构在向下游发展时是非常规整的, 形成了相互干扰又彼此独立的拟序结构. 在图 8(a)该周期开始时刻, 上部尖劈出现诱导涡分离现象; 到图 8(b)Tp/4时刻上部诱导涡发育完全, 脱离尖劈向下游运动; 到图 8(c)Tp/2时刻下部尖劈开始产生诱导涡; 到图 8(d)3Tp/4时刻下部诱导涡发育完全, 也向下游运动; 到图 8(e)t=Tp时刻上部尖劈又产生新的诱导涡. 如此循环往复, 构成了非对称尖劈诱导Karman涡街的非定常流动过程.

|
| 图 7 非对称尖劈绕流的物理空间网格 Fig.7 Grid system in physical space for flow past an asymmetric wedge |
|
| 图 8 非对称尖劈绕流一个周期内的压力等值线云图 Fig.8 Pressure contours of flow past an asymmetric wedge in one period |
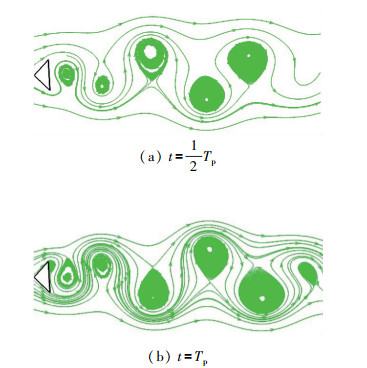
图 9给出了一个周期内t=Tp/2, t=Tp两个时刻的非对称尖劈绕流下游的涡系结构发展, 其中展示的是流线图. 可以看到, 非对称尖劈下游涡系结构比圆柱绕流下游的拟序结构要复杂得多, 前者上下尖角诱导产生的涡核大小略有差别, 且相隔半个周期的涡系结构并不关于y轴对称. 这些差异是由尖劈的非对称性引起的.
|
| 图 9 尖劈下游涡系结构 Fig.9 Vortex at the wake-region of flow past an asymmetric wedge |
本文在气体动理论统一算法框架下, 应用离散速度坐标法和3阶WENO格式, 以及3阶Runge-Katta时间推进法, 数值求解考虑转动自由度影响的Rykov模型方程, 得到了能模拟双原子气体跨流域非定常流动问题的一种确定论数值计算方法. 对经典的二维Karman涡街非定常流动现象的模拟, 说明了该跨流域非定常模拟方法能够适用于连续流区的低速流动, 并复现了关于Karman涡街流动现象的一些规律和理论:
(1) 低速圆柱绕流的Karman涡街是由于流动演化的对称性破缺而产生周期性变化规律, 与圆柱外形、流场网格等无关;
(2) 圆柱绕流的Karman涡街不仅在时间上有周期性变化规律, 而且圆柱上下诱导产生的拟序结构在空间上也具有对称性, 这种空间对称性并不体现在同一时刻, 而是体现在半个周期上的空间对称;
(3) 圆柱绕流的诱导涡产生必然是发生在圆柱上下顶点靠后的逆压梯度区;
(4) 非对称尖劈诱导产生的Karman涡街并不具有空间对称性, 但依然表现出时间上的周期性变化, 且其涡系结构更加复杂.
致谢 本工作得到973计划(2014CB744100), 国家自然科学基金(11902339, 11325212)资助.| [1] |
Boltzmann L. Weitere studien uber das warmeg-leichgewicht unter gasmolekulen[J]. Sitzungs Berichte Kaiserl. Akad. Der Wissenschaften, 1872, 66(2): 275-370. |
| [2] |
Chapmann S, Cowling T G. The mathematical theory of non-uniform gases[M]. 3rd ed. Cambridge: Cambridge University Press, 1990.
|
| [3] |
李启兵, 徐昆. 气体动理学格式研究进展[J]. 力学进展, 2012, 42(5): 522-537. Li Q B, Xu K. Progress in gas-kinetic scheme[J]. Advances in Mechanics, 2012, 42(5): 522-537. (in Chinese) |
| [4] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一算法研究[J]. 空气动力学学报, 2003, 21(3): 255-266. Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to contin-uum[J]. Acta Aerodynamica Sinica, 2003, 21(3): 255-266. DOI:10.3969/j.issn.0258-1825.2003.03.001 (in Chinese) |
| [5] |
Agarwal R K, Tcherimmissine F G. Computation of hypersonic shock wave flows of diatomic gases and gas mixtures using the generalized Boltzmann equation[R]. AIAA 2010-813, 2010.
|
| [6] |
Kolobov V I, Arslanbekov R R. Towards adaptive kinetic-fluid simulations of weakly ionized plasmas[J]. Journal of Computational Physics, 2012, 231: 839-869. DOI:10.1016/j.jcp.2011.05.036 |
| [7] |
Chigullapalli S, Alexeenko A. Unsteady 3D rarefied flow solver based on Boltzmann-ESBGK model kinetic equa-tions[R]. AIAA 2011-3993, 2011.
|
| [8] |
Polikarpov A P, Graur I. Unsteady rarefied gas flow through a slit[J]. Vacuum, 2014, 101: 79-85. DOI:10.1016/j.vacuum.2013.07.006 |
| [9] |
Lihnaropoulos J, Valougeorgis D. Unsteady vacuum gas flow in cylindrical tubes[J]. Fusion Engineering and Design, 2011, 86(9/11): 2139-2142. |
| [10] |
Chen S Z, Guo Z L, Xu K. Simplification of the unified gas kinetic scheme[J]. Physical Review E, 2016, 94(2): 023313. DOI:10.1103/PhysRevE.94.023313 |
| [11] |
Liu C, Xu K. A unified gas kinetic scheme for continuum and rarefied flows V: multiscale and multi-component plasma transport[J]. Communications in Computational Physics, 2017, 22(5): 1175-1223. DOI:10.4208/cicp.OA-2017-0102 |
| [12] |
Guo Z L, Wang R J, Xu K. Discrete unified gas kinetic scheme for all Knudsen number flows. Ⅱ. Thermal compressible case[J]. Physical Review E, 2015, 91(3): 033313. DOI:10.1103/PhysRevE.91.033313 |
| [13] |
Li Z H, Zhang H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. DOI:10.1016/j.jcp.2003.08.022 |
| [14] |
Li Z H, Zhang H X. Numerical investigation from rarefied flow to continuum by solving the Boltzmann model equa-tion[J]. International Journal of Numerical Methods in Fluids, 2003, 42(4): 361-382. DOI:10.1002/fld.517 |
| [15] |
Li Z H, Zhang H X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry[J]. Journal of Computational Physics, 2009, 228(4): 1116-1138. DOI:10.1016/j.jcp.2008.10.013 |
| [16] |
Li Z H, Zhang H X, Fu S, et al. A gas kinetic algorithm for flows in microchannel[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(3): 261-270. |
| [17] |
Wu J L, Li Z H, Peng A P, et al. Numerical simulations of unsteady flows from rarefied transition to continuum using gas-kinetic unified algorithm[J]. Advances in Applied Mathematics and Mechanics, 2015, 7(5): 569-596. DOI:10.4208/aamm.2014.m523 |
| [18] |
Wu J L, Li Z H, Peng A P, et al. Numerical study on rarefied unsteady jet flow expanding into vacuum using the gas-kinetic unified algorithm[J]. Computers & Fluids, 2017, 155: 50-61. |
| [19] |
Li Z H, Peng A P, Zhang H X, et al. Rarefied gas flow simulations using high-order gas-kinetic unified algori-thms for Boltzmann model equations[J]. Progress in Aerospace Sciences, 2015, 74: 81-113. DOI:10.1016/j.paerosci.2014.12.002 |
| [20] |
Bhatnagar P L, Gross E P, Krook M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511-525. DOI:10.1103/PhysRev.94.511 |
| [21] |
Holway Jr J H. New statistical models for kinetic theory: methods of construction[J]. The Physics of Fluids, 1966, 9(9): 1658-1673. DOI:10.1063/1.1761920 |
| [22] |
Shakhov E M. Generalization of the Krook kinetic relaxation equation[J]. Fluid Dynamics, 1968, 3(5): 95-96. DOI:10.1007/BF01029546 |
| [23] |
Nagnibeda E, Kustova E. Non-equilibrium reacting gas flows: kinetic theory of transport and relaxation processes[M]. Berlin, Heidelberg: Springer, 2009.
|
| [24] |
张贺. 统一气体动理论格式分子振动模型研究[D]. 西安: 西北工业大学, 2015. Zhang H. Study on molecular vibrational model based on unified gas-kinetic scheme[D]. Xi'an: Northwestern Polytechnical University, 2015(in Chinese). |
| [25] |
Wang Z, Yan H, Li Q B, et al. Unified gas-kinetic scheme for diatomic molecular flow with translational, rotational, and vibrational modes[J]. Journal of Computational Physics, 2017, 350: 237-259. DOI:10.1016/j.jcp.2017.08.045 |
| [26] |
Liu S, Yu P B, Xu K, et al. Unified gas-kinetic scheme for diatomic molecular simulations in all flow regimes[J]. Journal of Computational Physics, 2014, 259: 96-113. DOI:10.1016/j.jcp.2013.11.030 |
| [27] |
彭傲平, 李志辉, 吴俊林, 等. 含振动能激发Boltzmann模型方程气体动理论统一算法验证与分析[J]. 物理学报, 2017, 66(20): 204703. Peng A P, Li Z H, Wu J L, et al. Validation and analysis of gas-kinetic unified algorithm for solving boltzmann model equation with vibrational energy excitation[J]. Acta Phyica Sinica, 2017, 66(20): 204703. DOI:10.7498/aps.66.204703 (in Chinese) |
| [28] |
Rykov V A. A model kinetic equation for a gas with rotational degrees of freedom[J]. Fluid Dynamics, 1975, 10(6): 959-966. DOI:10.1007/BF01023275 |
| [29] |
Rykov V A, Titarev V A, Shakhov E M. Shock wave structure in a diatomic gas based on a kinetic model[J]. Fluid Dynamics, 2008, 43(2): 316-326. DOI:10.1134/S0015462808020178 |
| [30] |
Rykov V A, Titarev V A, Shakhov E M. Numerical study of the transverse supersonic flow of a diatomic rarefied gas past a plate[J]. Computational Mathematics and Mathematical Physics, 2007, 47(1): 136-150. DOI:10.1134/S0965542507010149 |
| [31] |
张涵信, 沈孟育. 计算流体力学-差分方法的原理和应用[M]. 北京: 国防工业出版社, 2003. Zhang H X, Shen M Y. Computational fluid dynamics-fundamentals and applications of finite diffe-rence methods[M]. Beijing: National Defence Industry Press, 2003. (in Chinese) |
| [32] |
张涵信. 关于非定常流动的计算问题[C]. 第六届全国流体力学学术会议论文集, 上海: 中国力学学会, 2001: 23-31. Zhang H X. Numerical problems for unsteady flows[C]. 6th Countrywide Hydrodynamics Conference, Shanghai, 2001: 23-31(in Chinese). |
| [33] |
Shu C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[R]. NASA/CR-97-206253, ICASE Report No. 97-65, 1997.
|
| [34] |
邓小刚, 刘昕, 毛枚良, 等. 高精度加权紧致非线性格式的研究进展[J]. 力学进展, 2007, 37(3): 417-427. Deng X G, Liu X, Mao M L, et al. Advances in high-order accurate weighted compact nonlinear schemes[J]. Advances in Mechanics, 2007, 37(3): 417-427. DOI:10.3321/j.issn:1000-0992.2007.03.009 (in Chinese) |
| [35] |
Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [36] |
董双岭, 吴颂平. 关于卡门涡街形状稳定性的一点分析[J]. 水动力学研究与进展, 2009, 24(3): 326-331. Dong S L, Wu S P. An analysis of the stability of Karman vortex street configurations[J]. Chinese Journal of Hydrodynamics, 2009, 24(3): 326-331. (in Chinese) |
| [37] |
Schlichting H. 边界层理论[M]. 徐燕侯, 等, 译. 北京: 科学出版社, 1988. Schlichting H. Boundary layer theory[M]. Beijing: Science Press, 1979(in Chinese). |
| [38] |
von Kármán T. Uber den Mechanismus des Widerstands, den ein bewegter Korper in einer Flussigkeit erfahrt[J]. Gottingen Nachr. Math. Phys. Klasse, 1912, 12: 509-517. |
| [39] |
唐少杰, 庄逢甘, 忻鼎定. 卡门涡街的慢不稳定性[J]. 力学学报, 1996, 28(2): 129-134. Tang S J, Zhuang F G, Xin D D. On the slow instability of Karman vortex street[J]. Acta Mechanica Sinica, 1996, 28(2): 129-134. (in Chinese) |



