近年来, 随着航空科学技术的发展, 飞行器的功能得到了不断拓展, 无人机、微型飞行器、平流层飞艇等在军事和民用方面得到了广泛应用[1].这些飞行器大多工作在低Reynolds数条件下, 在该条件下翼型的气动性能问题得到了越来越多的关注.
不同于常规Reynolds数(一般指Re > 106)流动, 在低Reynolds数(一般指104 < Re < 106)情况下[2], 翼型的气动性能会急剧下降, 并伴随着强非线性效应, 最终表现为阻力系数增加, 升力系数下降等问题.经研究, 普遍认为翼型的气动性能恶化与流动的分离相关.在低Reynolds数条件下, 翼型的表面边界层抗逆压梯度能力变差, 上表面边界层比较容易产生流动分离.分离的剪切层以分离泡的形式存在, 由于Kelvin-Helmholtz机制的作用[3], 分离的剪切层会经历湍流的转捩并最终形成湍流边界层[4].
分离泡是不稳定的, 它的结构常常依赖于Reynolds数、翼型攻角、翼型表面曲率和来流的湍流度.分离泡的位置和强度对翼型的气动性能和飞行稳定性影响较大, 它的存在会造成升力的损失、气动噪声的增强和阻力的增加, 转捩后的湍流边界层也将产生高摩擦阻力.针对这种情况, 科研工作者对低Reynolds数翼型流动进行了大量的实验和数值模拟研究, 并积极探索有效的流动控制方法.
实验方面, Horton[5]针对层流分离泡进行了细致的研究, 发现其在低Reynolds数翼型绕流中广泛存在, 建立了层流分离泡模型. Mueller等[6]和Selig等[7]在不同湍流度条件下通过风洞实验研究了低Reynolds数翼型绕流, 发现边界层的分离、转捩和再附过程与翼型的气动性能密切相关. Elimelech等[8]利用水洞实验对翼型绕流进行了研究, 发现翼型绕流在低Reynolds数条件下存在从层流到湍流的3个转变过程. Burgmann等[9]利用PIV技术研究了绕SD7003翼型流动, 通过对展向结构的测量发现了一种“半月形”漩涡结构的存在.
数值模拟方面, Yuan等[10]在Re=6.0×104条件下对绕SD7003翼型流动进行了一系列的大涡模拟, 研究得到了低Reynolds数条件下的流动特征, 并分析了亚格子模型和网格分辨率对大涡模拟的影响. Hoarau等[11]通过直接数值模拟研究了三维绕NACA0012翼型流动的转捩过程. Deng等[12]在攻角α=4°和Re=1.0×105条件下通过直接数值模拟研究了绕NACA0012翼型流动的分离、转捩和再附过程、Kelvin-Helmholtz不稳定性等问题. Gageik等[13]在Re=5.0×105的条件下对NACA0012翼型进行了直接数值模拟, 研究了涡的产生机制以及网格对计算结果的影响.国内的叶建等[14]在低Reynolds数条件下通过直接数值模拟研究了二维绕NACA0012翼型流动, 并得到了流场在不同攻角时的特性.白鹏等[15-16]在不同Reynolds数条件下研究了绕SD8020翼型流动的分离涡结构随攻角的变化, 并提出了后缘分离泡模型.
翼型流动控制方面, 国内外许多学者对抑制流动分离的抽吸控制[17-19]进行了研究, 优化了抽吸控制的参数并取得了初步的控制效果; Shan等[20]在α=6°和Re=1.0×105条件下利用直接数值模拟研究了主动控制以及被动控制形式的涡流发生器在NACA0012翼型流动的应用, 发现主动控制相比于被动控制能更好抑制流动分离.文献[21-23]中研究了柔性行波模型即局部主动变形在翼型绕流控制中的应用. Munday等[24]、郭秋亭[25]、刘强等[26]研究了蒙皮的振动对流场结构的影响, 发现合适的振动可以抑制流动分离并改善流场结构.
在流动分离的众多控制方案中, 抽吸控制得到了广泛研究并取得了较为显著的控制效果.然而, 目前抽吸控制大多基于固定的抽吸系数, 并未参考流场内部信息, 而且优化的抽吸参数仅适合特定的流动状态.实际上, 在低Reynolds数翼型绕流中, 分离区前缘的边界层为层流, 并且具有远离壁面的法向速度, 如果在控制区域内采用反向控制方案[27], 理论上可以根据流场信息抽吸分离区内的低能流体并抑制流动的分离.另外, 反向控制方案在平板边界层和槽道湍流中得到了广泛研究并取得了较好的减阻控制效果, 然而其在翼型绕流中的应用还鲜有报道, 由于流动结构的不同, 控制方案的有效性还须进一步验证.本文尝试将反向控制方案分别应用于抑制流动分离和湍流边界层减阻控制中, 并研究控制效果与机理.
1 数值研究方法 1.1 数值方法本文采用隐式大涡模拟(implicit large eddy simulation, ILES)方法对低Reynolds数翼型绕流的主动控制问题进行了研究.控制方程为三维曲线坐标系下完整形式的N-S方程, 无黏项的离散采用一种高分辨率、耗散可控的低色散差分格式[28], 黏性项的离散采用4阶中心差分格式, 在对其中的法向导数计算时进行特殊处理以避免奇偶失联现象[29].为了尽可能减小几何诱导误差, 对几何不变量及其它几何量的计算采用了文献[30]中的方法.在时间推进方面, 采用稳定性好、收敛速度快的隐式双时间步LU-SGS方法.在边界条件的处理上, 采用基于特征变量的两步插值法以保证边界格式的精度并减小远场边界的非物理反射[31].
1.2 程序验证本节利用标准二维NACA0012翼型对不同攻角、Mach数、Reynolds数的绕流流场进行了数值模拟, 并将计算结果与参考文献[32-33]中的结果进行比较来验证本文求解程序的准确性.计算网格采用O型网格, 网格点设置为416×91, 流向Nx=416, 法向Nz=91, 其中垂向第1层网格高度为1×10-4C(C为弦长).
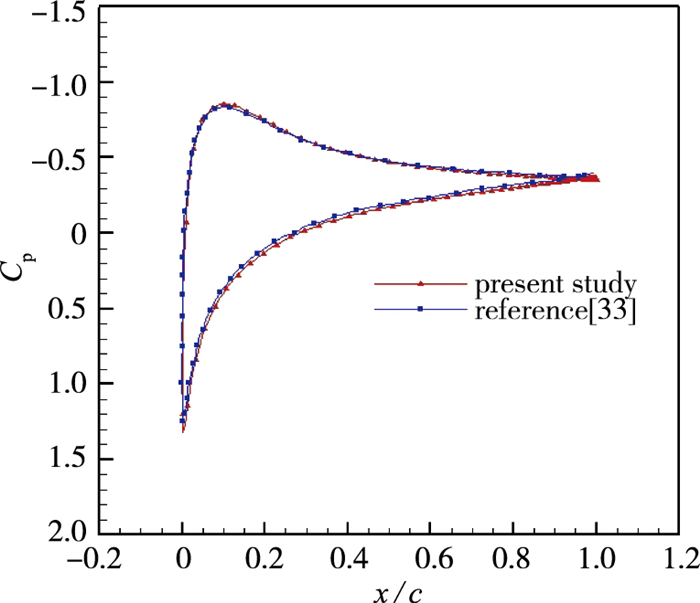
表 1给出了M=0.5, α=0°, Re=5 000条件下计算的分离位置与文献[32-33]的对比. 图 1给出了M=0.8, α=10°, Re=500时的压力系数, 表 2给出了该条件下的升力系数和阻力系数.
| 下载CSV 表 1 计算分离点与参考值比较 Tab.1 Comparisons of separation points |
|
| 图 1 M=0.8, α=10°, Re=500时计算结果 Fig.1 Results at M=0.8, α=10°, Re=500 |
| 下载CSV 表 2 计算结果与参考值比较 Tab.2 Comparisons of numerical results |
两组算例的计算结果均表明计算的分离点、升力系数和压差阻力系数与文献[32-33]吻合较好, 显示了本文求解程序的有效性与准确性.
1.3 计算网格针对α=6°, Re=1×105, M=0.2的三维绕NACA0012翼型流动, 本文通过隐式大涡模拟研究了边界层的分离及再附过程和分离泡的形成机制.
首先对网格的分辨率进行选择.本文选用5组计算网格对流场分别进行模拟: (1)208×40×61, (2)416×60×91, (3)600×60×101, (4)910×60×131, (5)1 300×80×151. 表 3中显示的是不同的网格分辨率情况下计算得到统计平均的分离点与再附点的位置.从表中可以看出, 当网格分辨率较低时计算结果偏差较大, 无法准确预测分离点和再附点的位置, 而随着网格的增多、分辨率的提高, 计算得到的统计平均分离点和再附点逐渐趋于稳定值.但是网格量的增加意味着计算量的急剧增大, 本文综合考虑了计算量和计算精度的要求, 选择mesh 4作为隐式大涡模拟的计算网格.
| 下载CSV 表 3 不同网格下的计算分离点与再附点比较 Tab.3 Comparisons of computational separation and reattachment points |
展向网格均匀分布, 近壁面第1层网格距离壁面5×10-5C.外边界采用远场边界条件, 内边界采用等温无滑移壁面边界条件, 展向边界采用周期性边界条件.由于采用无反射边界条件, 经过数值验证, 当远场边界取4C~6C时可以很好地模拟流场, 展向距离取0.06C.计算中自由来流湍流度为0.08%, 物理推进步长取Δt=1×10-5C/U∞.
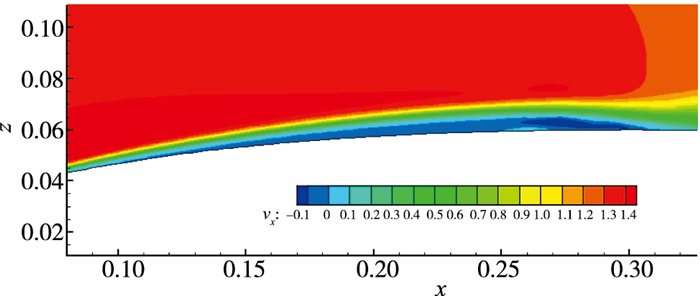
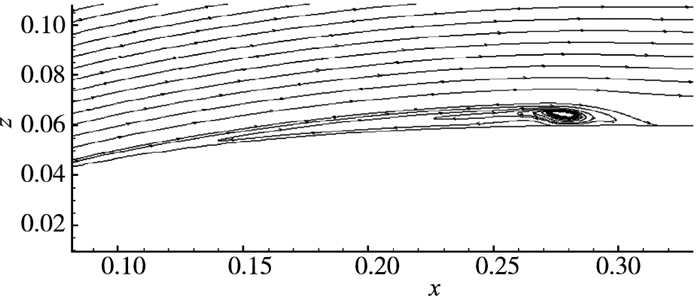
2 低Reynolds数翼型绕流的隐式大涡模拟 2.1 统计平均流场特征当流动状态稳定时, 对流场信息进行了统计平均处理.本节中显示的计算结果均为流场展向平均后再进行时间平均的结果. 图 2显示的是平均流向速度云图.从图中可以看出, 流动在x=0.09C处发生分离, 在x=0.31C处实现再附, 整个分离泡的平均长度为0.22C. 图 3中显示的是统计平均的流线图, 图中不仅显示了分离点与再附点的位置, 也显示了分离泡的中心位置, 约为x=0.27C.文献[34]中定义分离点至分离泡的中心为分离区的特征长度Lsep, 本节的计算结果为Lsep=0.18C.
|
| 图 2 时间和展向平均的流向速度分布 Fig.2 Contours of streamwise velocity after time and spanwise average |
|
| 图 3 时间和展向平均的流线图 Fig.3 Time and spanwise averaged streamlines |
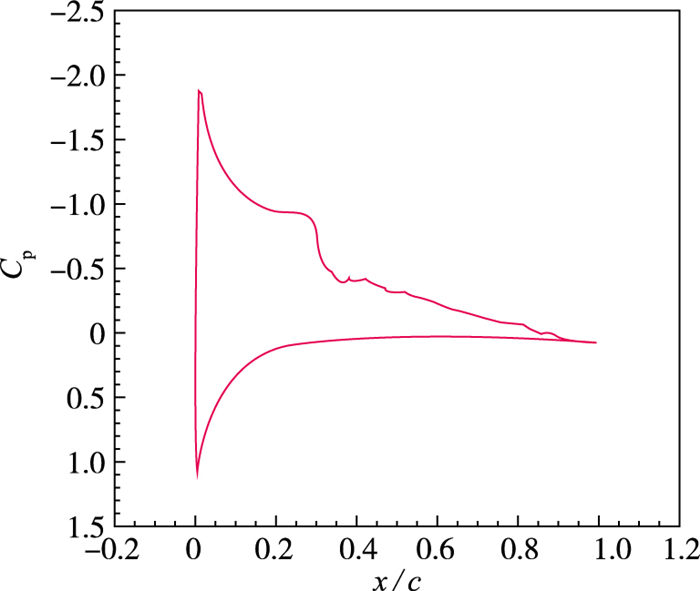
图 4给出了翼型表面的平均压力系数曲线, 可以看出由于较强的逆压梯度, 在前缘x=0.09C处出现了流动分离, 此后的分离区为低压低速水平段.在x=0.31C附近由于湍流的转捩, 使得翼型表面逆压梯度再次形成, 加速了回流流动的速度.
|
| 图 4 压力系数 Fig.4 Mean pressure coefficients |
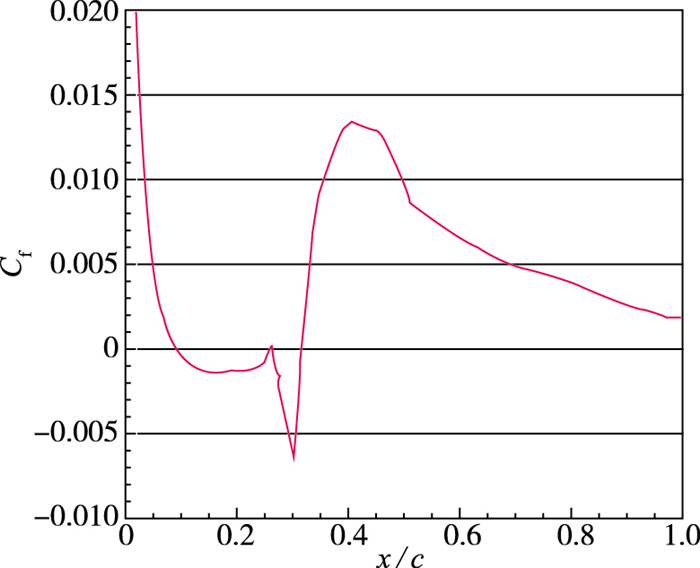
图 5给出了翼型表面的摩擦阻力系数曲线, 可以看出在x=0.09C~0.25C以及x=0.27C~0.31C区域摩擦系数为负值, 相应于分离泡的回流流动.在x=0.25C位置处, 摩擦系数迅速变化且此时湍动能急剧增加, 表明此时流动开始由层流向湍流转捩.
|
| 图 5 摩擦阻力系数 Fig.5 Mean skin friction coefficients |
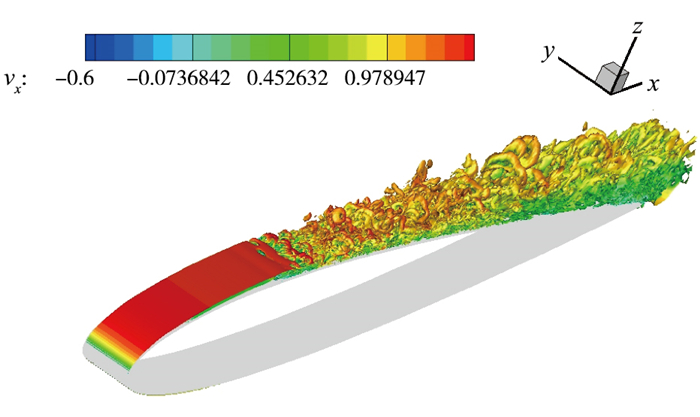
为了显示近壁区的涡结构, 本文利用Q判据对涡结构进行判别.翼型上表面的三维涡结构如图 6所示, 其中颜色分布代表流向速度vx大小.图中直观地显示了涡的形成、发展、脱落直至破碎的过程.在层流边界层向湍流转捩之前, 自由剪切层呈现二维特征, 从前缘开始与翼型上壁面分离并沿着流向分离逐渐变大; 平均在x≈0.25C附近, 剪切层在展向开始扭曲并出现涡的脱落, 而脱落的二维涡结构迅速扭曲断裂并最终发展为不同尺度发卡涡结构.此时的边界层也正经历从层流向湍流的转捩过程.转捩后的边界层由于较强的湍流剪切应力带入了外界的能量, 使得湍流边界层在x=0.31C附近实现再附.
|
| 图 6 流向涡等值面 Fig.6 Streamwise vortex isosurface |
从上节的计算中得到, 在α=6°, Re=1×105, M=0.2的条件下, 分离泡的长度为0.22C, 较长分离泡的存在会对翼型的气动性能和稳定性带来不利影响, 而且层流边界层向湍流的转捩使得翼型表面的摩擦阻力系数显著增加.本节我们尝试在翼型前缘利用壁面垂向反向控制方案对绕翼型流动进行控制, 期望通过控制减弱流动分离, 推迟湍流的转捩, 改善翼型的气动性能.
3.1 反向控制算法壁面垂向反向控制方案即在壁面处施加与边界层某位置大小相等方向相反的垂向速度.其具体的算法如下[27]:
| $ \phi _{\rm{w}}^{+}({{t}_{n+1}})=-w_{\rm{s}}^{+}({{t}_{n}}) $ |
其中, ws+(tn)为n时刻流场中某探测位置的垂向速度, ϕw+(tn+1)为n+1时刻在壁面处施加的垂向速度.在实际操作中, 通过在探测到的速度上乘以系数k改变控制的幅度, 此时算法为:
| $ \phi _{\rm{w}}^{+}({{t}_{n+1}})=-kw_{\rm{s}}^{+}({{t}_{n}}) $ |
由2.1节可知, 流场在x=0.09C处发生分离, 参照文献[20]的流场控制位置, 本节在x=0.1C~0.15C处, 在上壁面实施壁面垂向反向控制.然而在x=0.1C~0.15C处, 边界层为层流, 并不满足壁面湍流分层模型, 为了方便叙述, 类比于湍流边界层将壁面参数无量纲化, 并取
| $ {{y}^{+}}=y{{u}_{\tau }}/\nu $ |
其中, uτ是以壁面应力定义的壁湍流速度尺度.本节共选取了y+=10, 12, 14这3个探测位置; 控制参数k取为k=1, 具体参数如表 4所示.
| 下载CSV 表 4 反向控制的控制参数 Tab.4 Parameters values for opposition control scheme |
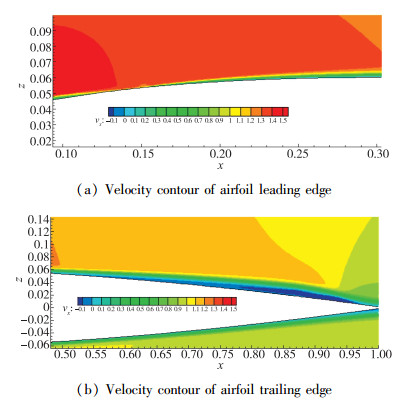
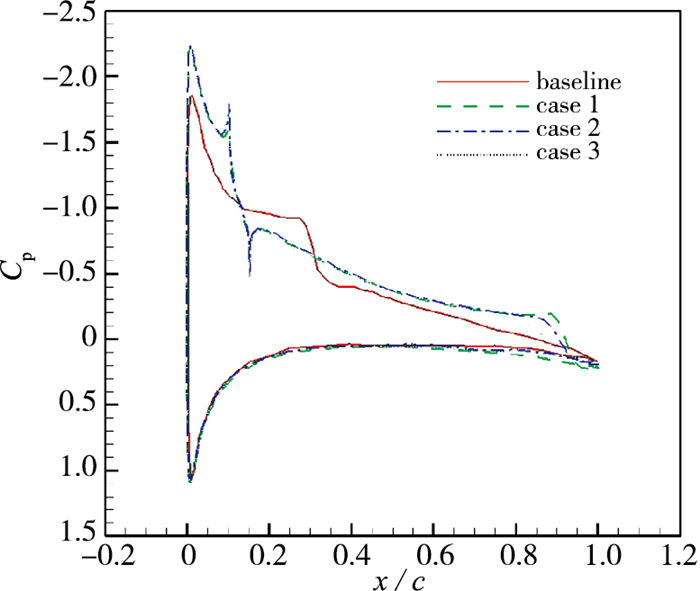
在下文的计算结果中, baseline代表未加控制的流场, case 1表示算例1, case 2表示算例2, case 3表示算例3. 图 7显示的是y+=12, k=1时的平均速度分布.从图中可以看出, 反向控制有效地抑制了翼型前缘的流动分离, 并将转捩点推迟到了尾缘.由于探测位置处流体具有沿上壁面法向离开的速度分量, 因此在此处实施反向控制相当于壁面抽吸, 然而与传统的抽吸控制不同的是, 反向控制依赖于流场内某探测位置处的流动信息, 控制具有实时性和高效性.反向控制的应用吸除了前缘边界层内低能量的流体, 使得附面层变薄, 同时增加了流动动量, 这增强了边界层抗逆压梯度能力.流动动量的增加也使得前缘壁面处压力变低, 这与图 8中压力系数的变化一致.从图中还可以看出转捩点的后移使得上壁面压力保持较低值, 这也是升力系数增加的原因.
|
| 图 7 y+=12, k=1时翼型表面的速度分布 Fig.7 Velocity contours at y+=12, k=1 |
|
| 图 8 压力系数 Fig.8 Mean pressure coefficients |
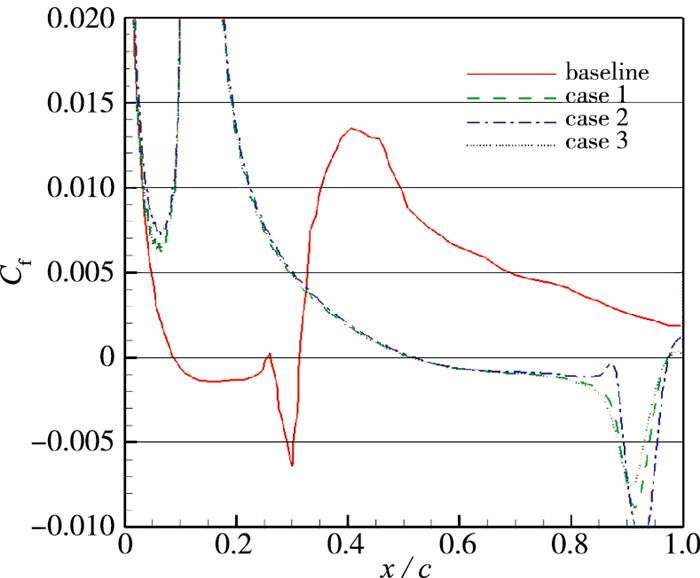
图 9给出了翼型上表面摩擦阻力系数沿弦长的分布, 在控制区域0.1C~0.15C位置处阻力系数增长较大, 这是因为在壁面处对低能流体的抽吸加强了边界层内的剪切流动, 抽吸系数越大, 剪切力也越大, 图中的结果反映了探测位置在y+=10, 12, 14的反向控制在壁面处的抽吸系数过大, 这也是y+分别为10, 12, 14时3种控制方案的计算结果相差不大的原因. 表 5给出了反向控制之后升力系数和摩擦阻力系数的变化, 其中升力系数提高了约15%, 而摩擦阻力系数则增大了29%左右.
|
| 图 9 阻力系数 Fig.9 Mean skin friction coefficients |
| 下载CSV 表 5 控制后的升力系数和摩阻系数 Tab.5 Lift and skin friction coefficients after control |
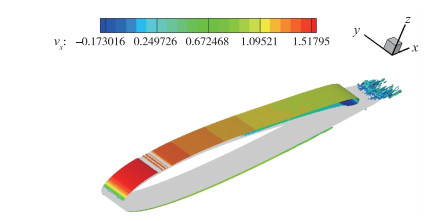
图 10给出了y+=12时流动的涡结构, 直观地显示了边界层的变化.经过流动控制, 附面层变薄并在较大范围内保持了层流流动, 但在边界层内沿着流向逆压梯度不断变大, 在翼型中部x=0.52C附近出现流动分离并在尾部x=0.95C附近实现流动再附, 形成长度约为0.43C的回流区.
|
| 图 10 y+=12, k=1时的流向涡等值面 Fig.10 Streamwise vortex isosurface at y+=12, k=1 |
计算结果显示当控制幅度k=1时, 反向控制有效抑制了翼型前缘的流动分离并将湍流转捩位置推迟到了尾缘, 这对提高翼型前缘的稳定性而言具有重要意义; 然而由于抽吸系数过大, 翼型表面摩擦阻力系数并未得到有效降低.为了在保证控制分离效果的同时有效降低摩擦阻力, 我们尝试适当缩小反向控制的控制幅度.下文测试y+=12, k为0.10时的反向控制方案.计算结果中, baseline代表未加控制的流场, case 2表示算例2, case 4表示k=0.10时的流场.
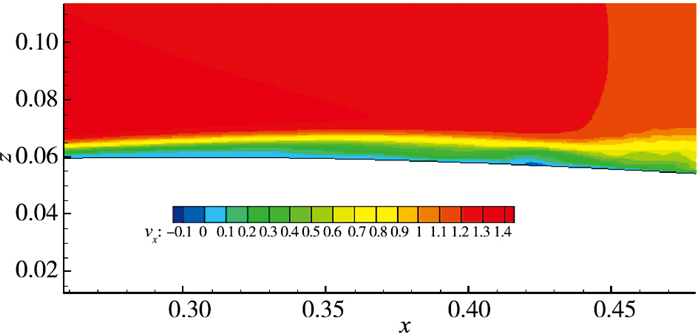
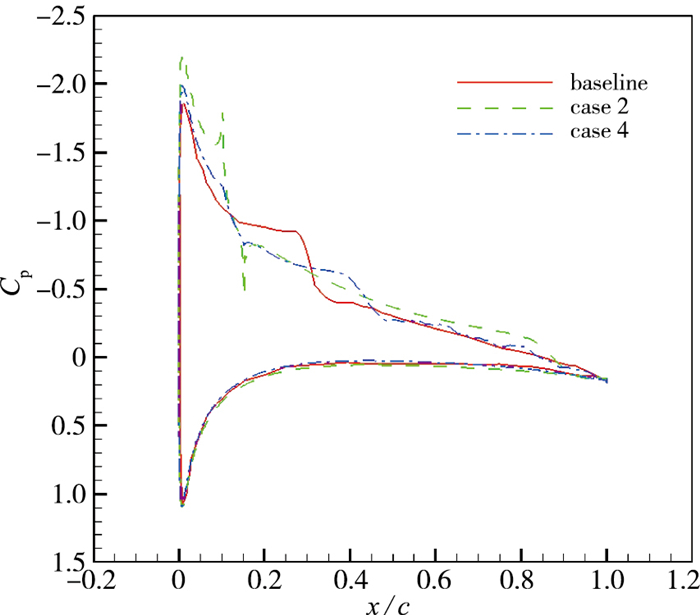
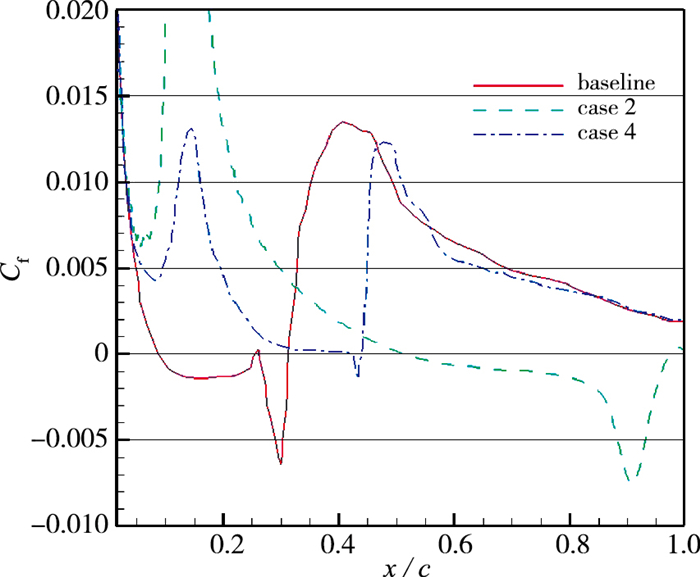
图 11显示的是翼型表面的平均流向速度分布, 图 12和图 13分别为压力系数与阻力系数.从图中可以看出, 当y+=12, k=0.10时的反向控制同样有效控制了翼型前缘的流动分离, 增强了其抗逆压梯度的能力, 推迟了转捩, 并在x=0.42C~0.43C之间形成了长度约为0.01C的短分离泡. 图 13中显示当k=0.10时控制区域阻力系数相比于k=1时得到了大幅度降低, 证明了适当缩小反向控制方案的控制幅度可以在保持控制效果的同时有效降低壁面摩擦阻力系数, 这对提高翼型气动性能而言非常重要.
|
| 图 11 y+=12, k=0.10时翼型表面的平均流向速度分布 Fig.11 Velocity contours at y+=12, k=0.10 |
|
| 图 12 压力系数 Fig.12 Mean pressure coefficients |
|
| 图 13 阻力系数 Fig.13 Mean skin friction coefficients |
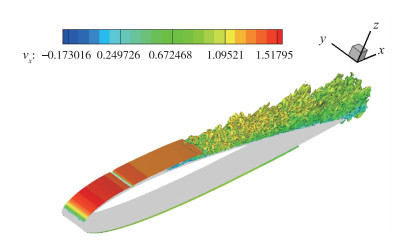
表 6直观地给出了缩小控制幅度后升力系数和摩擦阻力系数的变化, 其中升力系数提高了3%, 而阻力系数仅增大了4%左右. 图 14为y+=12, k=0.10时的流向涡等值面, 直观地给出了边界层以及流向涡的变化.
| 下载CSV 表 6 控制后的升力系数和摩阻系数 Tab.6 Lift and skin friction coefficients after control |
|
| 图 14 y+=12, k=0.10时的流向涡等值面 Fig.14 Streamwise vortex isosurface at y+=12, k=0.10 |
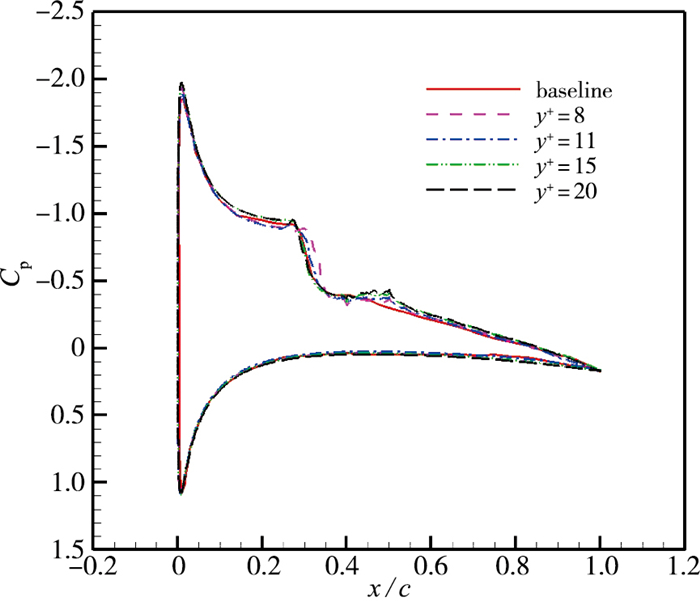
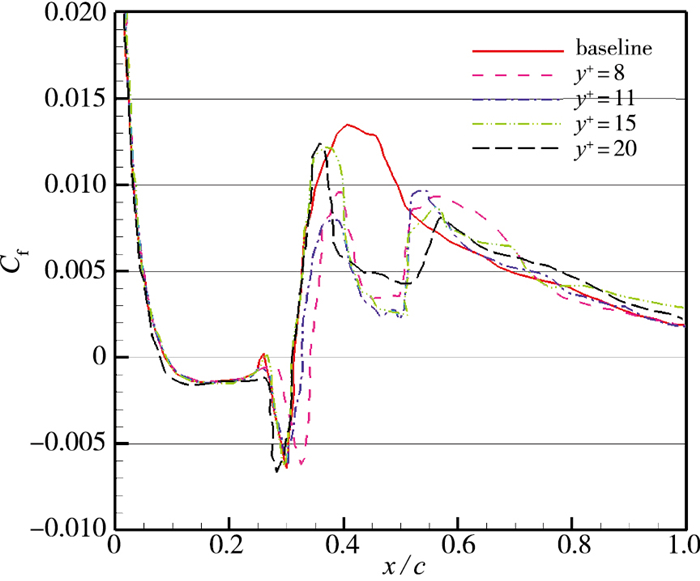
本节测试壁面垂向反向控制方案在翼型绕流中对湍流边界层的控制效果.取控制区域为x=0.4C~0.5C, k=1, 探测位置分别取y+=8, 11, 15, 20.控制前后的计算结果如图 15, 16所示.其中baseline代表未加控制的流场.图中给出的是控制前后压力系数和上壁面摩擦阻力系数的变化, 从图中可以看出, 施加反向控制后, 压力系数曲线除了在控制区域有轻微的波动外没有较大变化, 而控制区域的壁面摩擦阻力系数相比于控制之前有显著变化. 表 7给出的是控制后的升阻力系数变化情况, 结果显示4种控制方案均取得了一定减阻效果, 而当y+=11减阻效果最好, 阻力系数减小了27%左右.
|
| 图 15 压力系数 Fig.15 Mean pressure coefficients |
|
| 图 16 阻力系数 Fig.16 Mean skin friction coefficients |
| 下载CSV 表 7 控制后的升力系数和摩阻系数 Tab.7 Lift and skin friction coefficients after control |
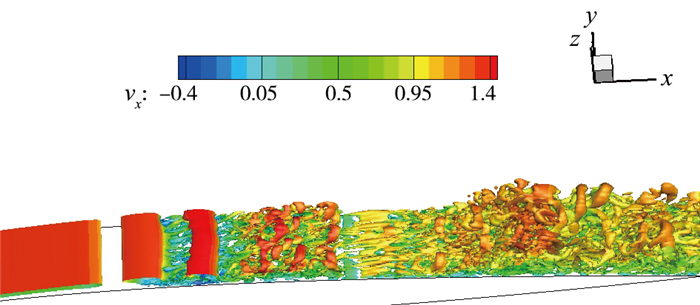
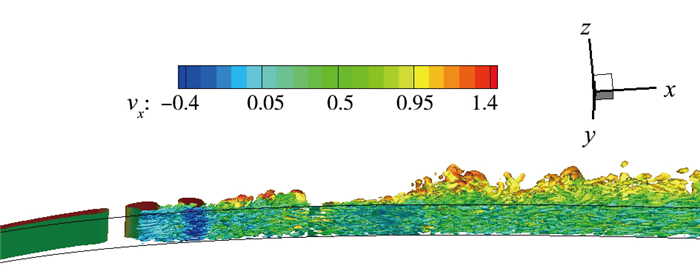
y+=11时的近壁区瞬时涡结构如图 17和图 18所示, 图 17为涡结构的俯视图, 而图 18显示的是从壁面朝上的仰视图.图中直观地显示了涡结构在控制前后的变化, 控制后近壁区的流向涡结构明显减少, 而且壁面处的流向速度也明显低于未控制区域.实际上反向控制的作用相当于在壁面和探测位置之间形成了虚拟壁面, 阻断了流向涡在法向的输运, 从而减少了控制区域内的涡结构, 减弱了猝发过程, 使得高摩阻力得到有效降低, 这也解释了图 16摩擦阻力系数在控制区域得到有效降低的原因.
|
| 图 17 流向涡等值面(俯视图) Fig.17 Streamwise vortex isosurface(downward view) |
|
| 图 18 流向涡等值面(仰视图) Fig.18 Streamwise vortex isosurface (upward view) |
本文利用隐式大涡模拟对低Reynolds数条件下的三维绕NACA0012翼型流动进行了研究, 并在此基础上尝试利用反向控制方案对翼型绕流中的分离区和湍流边界层分别进行了控制研究.主要结论为:
(1) 反向控制方案应用于分离区前缘部分时相当于基于流场某探测位置信息的壁面抽吸控制, 控制具有实时性和高效性.当探测位置为y+=10, 12, 14时, 控制抽吸了前缘的低能流体, 使得附面层变薄并增强了其抗逆压梯度能力, 使转捩点推迟到了尾缘, 同时增加了升力系数; 但由于抽吸系数过大, 增强了控制区域的剪切流动, 并未有效降低摩擦阻力系数.适当减小控制幅度时, 反向控制方案在保持控制分离效果的同时, 有效降低了壁面摩擦阻力系数, 较大提高了翼型气动性能.
(2) 反向控制方案应用于湍流边界层时, 在探测位置与固体壁面之间形成了虚拟壁面, 有效阻断了流向涡的法向输运, 并抑制了猝发过程, 从而有效减小了壁面处的高摩擦阻力.计算发现当y+=8, 11, 15, 20时反向控制均一定程度减小了壁面摩擦阻力, 而当y+=11时控制减阻效果最好, 证明了在平板或槽道湍流中具有较好控制效果的控制方案在翼型绕流中依然有效.
(3) 反向控制方案在分离区和湍流边界层均取得了较好的控制效果, 这也为下一步对低Reynolds数翼型绕流制定统一有效的流动控制方案提供了依据.
| [1] |
Selig M S, Guglielmo J J. High-lift low Reynolds number airfoil design[J]. Journal of Aircraft, 1997, 34(1): 72-79. DOI:10.2514/2.2137 |
| [2] |
冉景洪, 刘子强, 白鹏. 相对厚度对低雷诺数流动中翼型动态气动力特性的影响[J]. 空气动力学学报, 2008, 26(2): 178-185. Ran J H, Liu Z Q, Bai P. The effect of relative thickness to the dynamic aerodynamic characteristics about pitching airfoils[J]. Acta Aerodynamica Sinica, 2008, 26(2): 178-185. (in Chinese) |
| [3] |
Alam M, Sandham N D. Direct numerical simulation of short' laminar separation bubbles with turbulent reattachment[J]. Journal of Fluid Mechanics, 2000, 410(1): 1-28. |
| [4] |
Lumley J L. Flow control:passive, active and reactive flow management by mohamed Gad-el-Hak[J]. SIAM Review, 2001, 43(4): 726-727. |
| [5] |
Horton H P. Laminar separation bubbles in two and three dimensional incompressible flow[D]. London: Queen Mary University of London, 1968. http://www.researchgate.net/publication/285599356_Laminar_separation_bubbles_in_two_and_three-dimensional_incompressible_flow
|
| [6] |
Mueller T J, Batil S M. Experimental studies of separa-tion on a two-dimensional airfoil at low Reynolds numbers[J]. AIAA Journal, 2015, 20(4): 457-463. |
| [7] |
Selig M, Guglielmo J, Broern A, et al. Experiments on airfoils at low Reynolds numbers[C]. 34th Aerospace Sciences Meeting and Exhibit, Reno: AAIA, 2013. http://www.researchgate.net/publication/269078444_Experiments_on_airfoils_at_low_Reynolds_numbers?_sg=Mell-W9PkGY8vU7jgni49oH__o9I3xTvwVjVJgdhgwLAm9nyEYQcS6n6oYUOESQgfFpgALOKW_zxlp2EHZQz8Q
|
| [8] |
Elimelech Y, Arieli R, Iosilevskii G. On the onset of transition at low Reynolds number flow over airfoils[C]. 4th AIAA Theoretical Fluid Mechanics Meeting, Toronto, Ontario, Canada: AIAA, 2013. https://arc.aiaa.org/doi/abs/10.2514/6.2005-5311
|
| [9] |
Burgmann S, Brücker C, Schröder W. Scanning PIV measurements of a laminar separation bubble[J]. Experiments in Fluids, 2006, 41(2): 319-326. DOI:10.1007/s00348-006-0153-6 |
| [10] |
Yuan W, Xu H, Khalid M, et al. A parametric study of LES on laminar-turbulent transitional flows past an airfoil[J]. International Journal of Computational Fluid Dyna-mics, 2006, 20(1): 45-54. DOI:10.1080/10618560600578492 |
| [11] |
Hoarau Y, Braza M, Ventikos Y, et al. Organized modes and the three-dimensional transition to turbulence in the incompressible flow around a NACA0012 wing[J]. Journal of Fluid Mechanics, 2003, 496: 63-72. DOI:10.1017/S0022112003006530 |
| [12] |
Deng S T, Jiang L, Liu C Q. DNS for flow separation control around an airfoil by pulsed jets[J]. Computers & Fluids, 2007, 36(6): 1040-1060. |
| [13] |
Gageik M, Klioutchnikov I, Olivier H. Comprehensive mesh study for a direct numerical simulation of the transonic flow at Rec=500000 around a NACA0012 airfoil[J]. Computers & Fluids, 2015, 122: 153-164. |
| [14] |
叶建, 林国华, 邹正平, 等. 低雷诺数下二维翼型绕流的流场特性分析[J]. 航空动力学报, 2003, 18(1): 38-45. Ye J, Lin G H, Zou Z P, et al. The analysis of flow around a 2-D airfoil at low Reynolds number[J]. Journal of Aerospace Power, 2003, 18(1): 38-45. (in Chinese) |
| [15] |
白鹏, 崔尔杰, 李锋, 等. 对称翼型低雷诺数小攻角升力系数非线性现象研究[J]. 力学学报, 2006, 38(1): 1-8. Bai P, Cui E J, Li F, et al. Study of the nonlinear lift coefficient of the symmetrical airfoil at low Reynolds number near the 0ångle of attack[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 1-8. (in Chinese) |
| [16] |
白鹏, 崔尔杰, 周伟江, 等. 翼型低雷诺数层流分离泡数值研究[J]. 空气动力学学报, 2006, 24(4): 416-424. Bai P, Cui E J, Zhou W J, et al. Numerical simulation of laminar separation bubble over 2D airfoil at low Reynolds number[J]. Acta Aerodynamica Sinica, 2006, 24(4): 416-424. (in Chinese) |
| [17] |
Huang L, Huang P G, LeBeau R P, et al. Numerical study of blowing and suction control mechanism on NACA0012 airfoil[J]. Journal of Aircraft, 2004, 41(5): 1005-1013. DOI:10.2514/1.2255 |
| [18] |
张旺龙. 低雷诺数下附面层分离的抽吸控制及优化[D]. 南京: 南京理工大学, 2014. Zhang W L. Suction control and its optimization of boundary layer separation at low Reynolds numbers[D]. Nanjing: Nanjing University of Science and Technology, 2014(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10288-1016035477.htm |
| [19] |
Saeed T I, Graham W R, Hall C A. Boundary-layer suction system design for laminar-flying-wing aircraft[J]. Journal of Aircraft, 2011, 48(4): 1368-1379. DOI:10.2514/1.C031283 |
| [20] |
Shan H, Jiang L, Liu C Q, et al. Numerical study of passive and active flow separation control over a NACA0012 airfoil[J]. Computers & Fluids, 2008, 37(8): 975-992. |
| [21] |
Sahin M, Sankar L N, Chandrasekhara M S, et al. Dynamic stall alleviation using a deformable leading edge concept-a numerical study[J]. Journal of Aircraft, 2012, 40(1): 77-85. |
| [22] |
Lee B S, Ye K, Joo W, et al. Passive control of dynamic stall via nose droop with gurney flap[C]. 43rd AIAA Aero-space Sciences Meeting and Exhibit, Reno, Nevada: AIAA, 2005. http://arc.aiaa.org/doi/abs/10.2514/6.2005-1364?mi=8emnlt&af=R&contents=articlesChapters&countTerms=true&field1=Contrib&target=default&text1=Lee%2C+Dong-Ho
|
| [23] |
吴介之. 涡动力学引论[M]. 北京: 高等教育出版社, 1993. Wu J Z. Introduction to vorticity and vortex dynamics[M]. Beijing: Higher Education Press, 1993. (in Chinese) |
| [24] |
Munday D, Jacob J. Active control of separation on a wing with oscillating camber[J]. Journal of Aircraft, 2002, 39(1): 187-189. DOI:10.2514/2.2915 |
| [25] |
郭秋亭. 局部主动变形翼型和折叠翼变形飞机动态气动特性数值模拟研究[D]. 绵阳: 中国空气动力研究与发展中心, 2009. Guo Q T. Numerical simulation of the dynamic aerodynamic characteristics about partial flexible airfoils and folding wing aircraft[D]. Mianyang: China Aerodynamics Research and Development Center, 2009(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-90113-2010024444.htm |
| [26] |
刘强, 刘周, 白鹏, 等. 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究[J]. 力学学报, 2016, 48(2): 269-277. Liu Q, Liu Z, Bai P, et al. Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at low Reynolds number[J]. Chinese Journal of Theoretical and Applied Mecha-nics, 2016, 48(2): 269-277. DOI:10.6052/0459-1879-15-188 (in Chinese) |
| [27] |
Choi H, Moin P, Kim J. Active turbulence control for drag reduction in wall-bounded flows[J]. Journal of Fluid Mechanics, 1994, 262: 75-110. DOI:10.1017/S0022112094000431 |
| [28] |
Sun Z S, Ren Y X, Larricq C, et al. A class of finite difference schemes with low dispersion and controllable dissipation for DNS of compressible turbulence[J]. Journal of Computational Physics, 2011, 230(12): 4616-4635. DOI:10.1016/j.jcp.2011.02.038 |
| [29] |
Shen Y Q, Yang B Y, Zha G C. Implicit WENO scheme and high order viscous formulas for compressible flows[C]. 25th AIAA Applied Aerodynamics Conference, Miami, Florida: AIAA, 2007.
|
| [30] |
Zhu Y J, Sun Z S, Ren Y X, et al. A numerical strategy for freestream preservation of the high order weighted essentially non-oscillatory schemes on stationary curvili-near grids[J]. Journal of Scientific Computing, 2017, 72(3): 1021-1048. DOI:10.1007/s10915-017-0387-x |
| [31] |
Sun Z S, Ren Y X, Zha B L, et al. High order boundary conditions for high order finite difference schemes on curvilinear coordinates solving compressible flows[J]. Journal of Scientific Computing, 2015, 65(2): 790-820. DOI:10.1007/s10915-015-9988-4 |
| [32] |
Mavriplis D J, Jameson A. Multigrid solution of the Navier-Stokes equations on triangular meshes[J]. AIAA Journal, 1990, 28(8): 1415-1425. DOI:10.2514/3.25233 |
| [33] |
Jameson A, Katz A J. Meshless methods for computational fluid dynamics[D]. Stanford, CA, USA: Stanford University, 2009. http://www.researchgate.net/publication/252815704_Meshless_methods_for_computational_fluid_dynamics
|
| [34] |
Mittal R, Kotapati R B, Cattafesta L. Numerical study of resonant interactions and flow control in a canonical separated flow[C]. 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada: AIAA, 2005. http://www.researchgate.net/publication/228662201_Numerical_study_of_resonant_interactions_and_flow_control_in_a_canonical_separated_flow
|



