在现代先进歼击机的设计中, 机动性的地位越来越重要, 例如第四代战斗机的4S标准中, 超机动性排在首位.在低速、大迎角、高俯仰速率下进行可控机动是战斗机超机动性的核心要求.在飞机进行低速大迎角、高俯仰速率的飞行过程中, 飞机周围的流场处于强非定常状态, 因此飞机的气动特性与定常状态有很大不同.从飞机试飞的结果来看, 在飞机进行大迎角俯仰机动时, 飞机升力会产生迟滞环[1].目前, 边条翼在歼击机中的应用十分广泛, 如俄罗斯的苏-27、我国的J-20等.边条翼布局的战斗机进行大迎角俯仰机动时, 其气动力也会产生迟滞环, 故研究带边条三角翼也就是双三角翼做大振幅俯仰机动时的流动特性、探究其迟滞现象背后的机理, 从而准确预测这种气动迟滞现象对当今先进歼击机的设计具有重要意义.
目前, 静态双三角翼的研究可分为两大方面, 气动力测量和流场测量. Mahon等[2-3]对75°/62°和80°/62°双三角翼进行了测力和实验, 结果表明双三角翼具有显著的增升作用.与单三角翼不同, 双三角翼流场最大的特征是存在两个涡, 一般把前面后掠角较大的边条前缘产生的涡叫边条涡, 把拐点之后的主翼前缘产生的涡叫做主翼涡. Hoeijmakers等[4]进行了双三角翼的片光流动显示实验, 实验表明, 主翼涡在拐点之后产生, 并在之前产生的边条涡的诱导速度作用下围绕边条涡旋转并最终与边条涡融合, 同时, 在主翼涡的作用下, 边条涡的轨迹也会发生明显的向外移动现象. Zhang等[5]利用PIV技术对70°/50°双三角翼的旋涡相互作用和非定常性进行了研究, 并与单三角翼的结果进行了对比, 发现双三角翼的主翼涡要比单三角翼的主翼涡更远离机翼上表面, 并且破裂得更早(即涡破裂迎角更小).他们还对PIV结果进行了POD分析, 并认为两个涡即使在距离很远的情况下依然存在很强的相互作用.
在双三角翼进行动态俯仰运动时, 其升力曲线会存在迟滞环, 前人关于动态双三角翼的研究主要集中在气动力测量和对涡破裂的分析两大方面. Den等[6-7]研究了76°/40°双三角翼小振幅(最大不超过16°)俯仰运动, 通过表面压力测量和流动显示实验对涡破裂进行了分析, 发现在双三角翼的小振幅俯仰实验中存在迟滞现象. Hebbar等[8]研究了不同俯仰频率下76°/40°双三角翼的定速俯仰运动, 在上仰时涡破裂位置较静态时滞后, 下俯时涡破裂位置提前. Grismer等[9]给出了不同缩减频率下80°/60°后掠角双三角翼的法向力系数和涡破裂位置随迎角的变化关系, 随着缩减频率的增加, 法向力系数的迟滞环增大, 涡破裂位置的滞后与提前都随缩减频率的增加而增加. Myose等[10]和Ericsson[11]的研究结果中也存在类似的现象. Liu等[12-13]利用DDES模型模拟了俯仰机动过程中双三角翼前缘涡的非定常特性和涡破裂现象.在80°/65°双三角翼在迎角为30°~42°之间进行俯仰运动时, 涡破裂位置与迎角之间存在大约90°的相位差.
在目前的研究中, 对于双三角翼俯仰的研究主要集中在较低的缩减频率下, 对于以较高缩减平台俯仰的研究较少, 特别是k>0.2时, 并且很少与单三角翼进行对比.在双三角翼的俯仰运动中, 边条的影响目前还存在疑问, 故本研究通过测力实验和数值模拟, 研究双三角翼在不同缩减频率下的非定常气动力特性, 并与单三角翼结果进行对比, 研究边条在不同俯仰缩减频率下的作用机制, 探究双三角翼在大振幅非定常俯仰过程中的流动机制, 为超机动性飞机的设计和改进提供理论依据.
1 实验及计算设置 1.1 实验设置 1.1.1 实验装置本项实验研究在北京航空航天大学沙河校区陆士嘉实验室的回流式水槽实验中开展, 水槽实验段的尺寸为4 000 mm(长)×400 mm(宽)×525 mm(高), 实验段的有效流速范围为0~0.5 m/s, 最大湍流度不超过1%, 研究使用的自由来流速度U∞= 0.15 m/s.
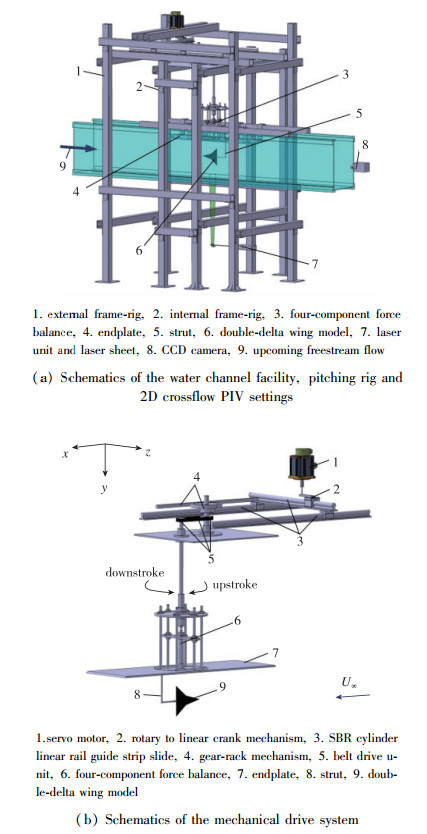
双三角翼的大振幅非定常俯仰运动由实验中搭建的俯仰运动平台实现, 如图 1所示.该平台主要由外部框架, 内部框架, 机械传动系统及控制与测量系统4大部分组成.外部框架用来支撑机械传动系统, 内部框架用来支撑模型和测力系统.为了尽可能减小机械振动对实验测量的影响, 内外部框架彼此互相独立并且采用皮带齿轮传动.机械传动系统由1台1 kW的台达伺服电机(ECMA-E31310H), 1个台达驱动器(ASDA1021AB), 1个12:1的减速器(PL20), 曲柄滑块机构, 齿轮齿条传动机构以及皮带齿轮传动机构组成(如图 1(b)所示).传动时, 曲柄滑块机构将伺服电机产生的圆周运动转化为类正弦运动, 经齿轮齿条和皮带齿轮传动机构将类正弦运动传递给模型.模型迎角会通过角度传感器传送给主控电脑.
|
| 图 1 实验装置示意图 Fig.1 Schematic diagram of experimental device |
模型非定常力用一个四分量测力天平测量, 天平量程为2 N.为保证天平不浸入水中, 将天平通过支杆与实验模型相连, 实验时先单独测量支杆受力, 在最终的测量结果中将支杆受力减去, 以消除支杆的影响.
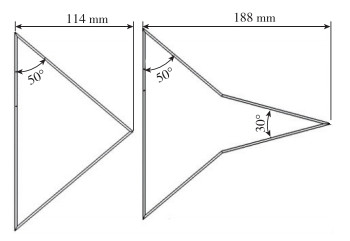
1.1.2 实验模型实验所用模型为边条后掠角为75°、主翼后掠角为50°的无弯度平板双三角翼模型和后掠角为50°的单三角翼模型(如图 2所示), 模型前缘和后缘双面45°倒角.双三角翼由铝合金板精加工而成, 主翼根弦长为114 mm, 总长188 mm, 厚度4 mm.俯仰运动的旋转轴与机翼根弦垂直, 距双三角翼后缘38 mm.三角翼的根弦长与双三角翼主翼根弦长相同, 为114 mm, 其他参数均与双三角翼模型相同.
|
| 图 2 实验模型 Fig.2 Experimental model |
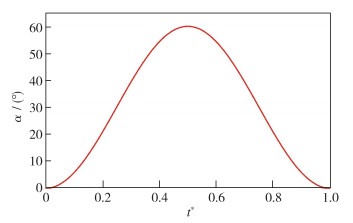
实验中自由来流的速度为0.15 m/s, 以主翼弦长为参考的Reynolds数为Re=1.69×104.实验中水洞的最大阻塞度不超过8%.双三角翼俯仰运动的迎角范围为0~60°, 运动形式为余弦函数, 运动的时间历程如图 3所示.在实验过程中, 双三角翼模型先上仰到60°, 再由60°下俯到0°, 完成一个周期的循环.
|
| 图 3 俯仰运动时间历程 Fig.3 Time history of pitching motion |
测力实验选取了5个俯仰频率, 分别为0.012 5, 0.25, 0.5, 0.1, 0.2 Hz.在机翼俯仰运动过程中, 来流速度与俯仰速度的比值为影响流动的决定性参数, 故取缩减频率k作为表示来流速度与俯仰速度比值的无量纲参数. k与俯仰频率f的关系为
| $ k = \frac{{\pi fc}}{{{U_\infty }}} $ |
实验的缩减频率分别为0.03, 0.06, 0.12, 0.24, 0.48.
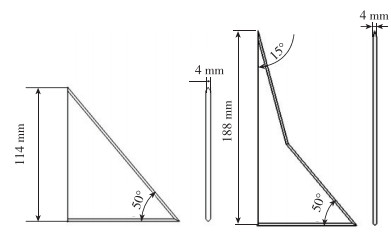
1.2 计算设置 1.2.1 计算模型与计算方法为减小网格数量, 提高计算精度, 本研究中的数值模拟采用半模进行计算.数值计算选用的模型参数与实验模型相同, 为50°三角翼半模和75°/50°双三角翼半模(如图 4所示).
|
| 图 4 计算模型 Fig.4 Numerical simulation model |
图 5为S75W50模型的数值网格在壁面附近的划分情况, 考虑到边条上存在前缘涡、二次分离等复杂的流动现象, 因此对该区域的网格进行加密; 因模型近壁面的速度梯度较大, 故在模型近壁面区域也进行了加密.

|
| 图 5 S75W50模型近壁区网格划分 Fig.5 Grid division in near wall area of S75W50 model |
数值模拟使用FLUENT软件平台, 控制方程采用有限体积法离散, 对流项采用2阶迎风格式, 扩散项采用中心差分格式, 压力与速度耦合方式采用SIMOLEC算法, 物面边界条件采用无滑移物面, 入口采用速度入口边界条件, 出口采用压力出口边界条件, 对称面采用对称边界条件.
数值模拟的湍流模型采用延迟分离涡模拟方法(delayed detached-eddy simulation, DDES). DDES方法是广义的RANS-LES混合模型的一种.由于单纯的RANS模型对由大范围分离流动占主导的复杂流场的模拟一直不太理想, 而LES对空间分离流场具有较好的模拟效果, 但是近壁区模拟须耗费大量的计算资源, Spalart等[14]针对这种情况提出了DDES模型, 该方法在物面附近采用RANS模型有效地处理边界层的流动, 在远离物面的流动区域内采用大涡模拟(LES)计算大范围分离流动, 这种方法综合了RANS和LES的优势, 改进了高Reynolds数下大分离流动的数值模拟能力.
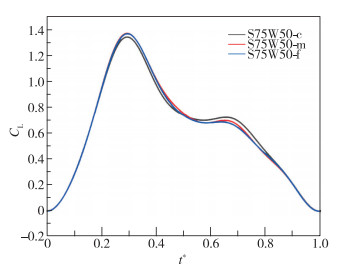
1.2.2 网格无关性验证为检验计算结果的精度与可靠性, 进行了网格无关性验证.分别绘制了3个不同密度的网格, 网格数量分别为3×106, 5×106和7×106, 分别利用3个网格计算了k=0.06时S75W50的升力曲线, 如图 6所示.
|
| 图 6 k=0.06时S75W50不同网格升力曲线 Fig.6 S75W50 lifting curves with different grids at k=0.06 |
由图 6可知, 当网格密度发生改变时, 3种网格计算出的曲线基本重合, 升力最大值及最大值取值位置如表 1所示.在3种不同的计算网格下, 最大升力系数和取得最大升力系数的迎角基本保持不变.因此, 可认为本研究中的数值模拟方法具有网格无关性.
| 下载CSV 表 1 网格数对升力最大值的影响 Tab.1 Effects of the girds on maximum lift |
为了尽可能地增加计算精度并减小计算资源, 本研究中的数值模拟采用网格数为5×106的medium网格.
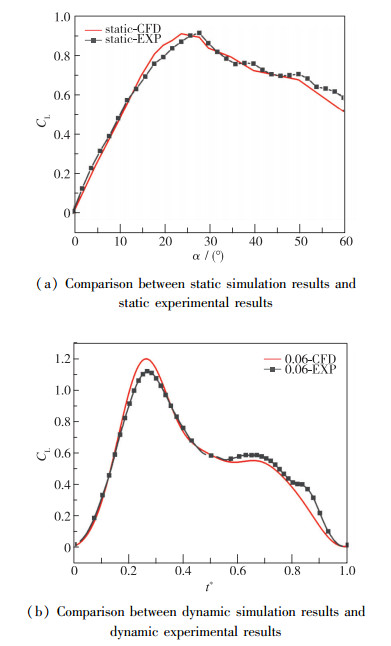
1.2.3 数值模拟精度验证首先,对比了静态下W50三角翼的计算结果与水槽实验结果, 如图 7(a)所示, 实验结果与计算结果近似.随后进行了动态结果的验证, 如图 7(b)所示, 实验结果与计算结果近似相同, 可证明本研究中的数值模拟结果具有较强的可靠性.
|
| 图 7 计算结果与实验结果对比 Fig.7 Comparisons between simulation results and experimental results |
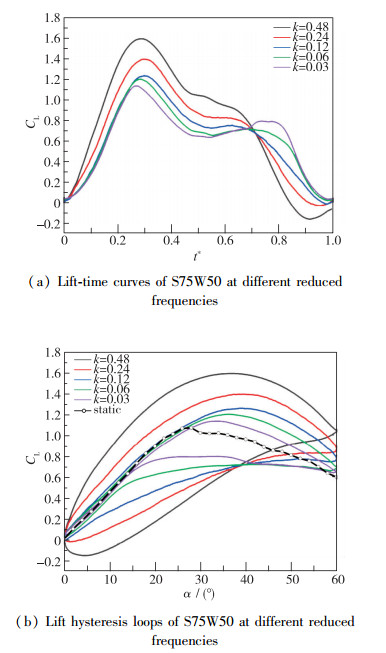
不同缩减频率下S75W50升力-时间曲线和迟滞环结果如图 8所示.
|
| 图 8 不同缩减频率S75W50升力结果 Fig.8 Lift results of S75W50 at different reduced frequencies |
由图 8(a)可知, 不同缩减频率下的S75W50升力-时间曲线在形状上具有相似性.在运动的开始阶段, 都存在一个快速的上升期, 但不同缩减频率下的斜率不同.当缩减频率k < 0.12时, 上升期的斜率相同, 曲线基本重合, 而当k>0.12时, 上升期的斜率明显增大.由图 6(b)迟滞环结果可知, 当k < 0.12时, 上升期升力曲线与静态时的升力曲线重合.这是因为当k较小时, 流动处于准非定常状态, 此时流场中的定常效应还不十分明显, 而随着缩减频率k的增大, 流场中的非定常效应占比越来越大, 因此其升力与静态时相比有较大的增量.
升力最大值所在位置随着缩减频率的变化而变化.当k < 0.12时, 升力的最大值位置随缩减频率的增加而向右移动, 当k>0.12时, 升力最大值位置几乎不变.升力最大值的位置与前缘涡的破裂位置密切相关, 较高的缩减频率能延缓前缘涡的破裂, 使双三角翼的失速迎角增大.
在达到升力最大值后, 5个工况下的升力系数都开始快速下降, 并在周期50%处, 也就是迎角为60°附近形成一段平台期.在此阶段, 升力系数随缩减频率的增加而增加.由模型的运动方程可知, 在最大迎角附近, 模型的俯仰角速度较小, 升力主要由在上仰时残留的旋涡结构诱导产生.随着缩减频率的增加, 机翼上表面残留的涡增加, 故在平台期能产生较大的升力.
在模型的下俯阶段, 缩减频率较小(k < 0.06)时, 升力出现了上升, 并且在迟滞环曲线中观察到下俯时的升力曲线与静态和上仰时几乎重合, 说明在此过程中机翼上表面的旋涡重新恢复, 为机翼提供涡升力, 随着缩减频率的增加, 旋涡恢复得更晚, 甚至完全没有恢复, 因此在下俯阶段随着缩减频率的增加, 机翼升力减小.
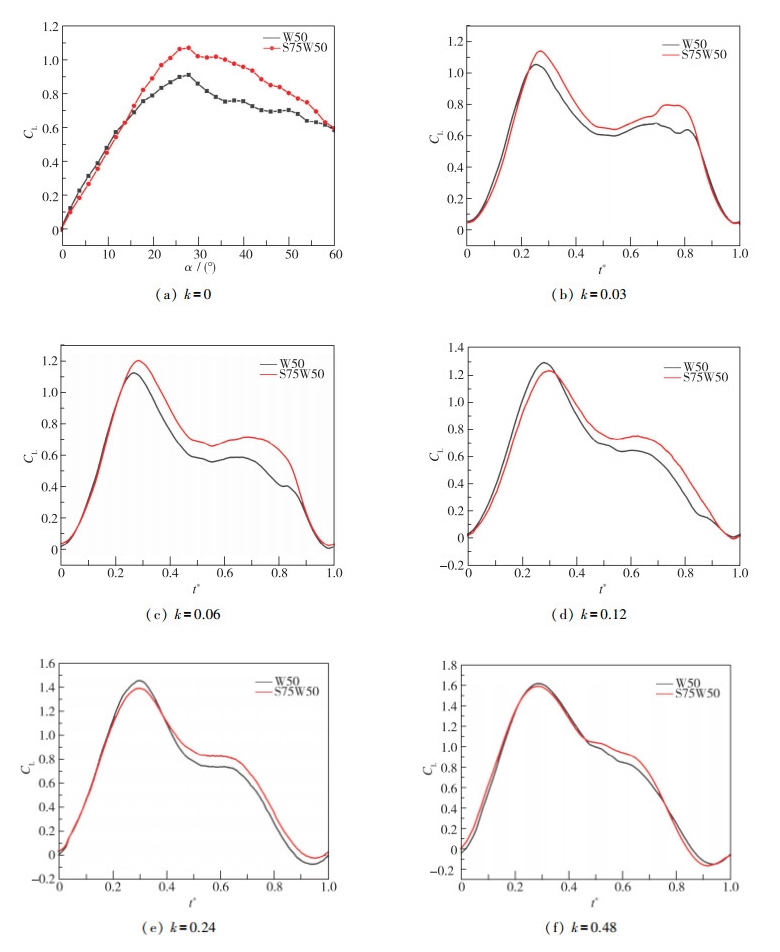
2.2 S75W50与W50测力结果对比分析S75W50与W50测力结果对比如图 9所示.在静态时, 由于S75W50的大后掠边条产生的前缘涡较强, 在18°迎角后, W50的前缘涡已经开始破裂, 使升力线斜率减小.而S75W50的前缘涡破裂较晚, 因此S75W50的升力系数较大.
|
| 图 9 不同缩减频率S75W50与W50升力结果对比 Fig.9 Comparisons of S75W50 and W50 lift results at different reduced frequencies |
在不同频率下, 上升期二者的升力近似相同.在k=0.03,0.06时, S75W50升力系数最大值较大, 而当k=0.12,0.24时, S75W50的升力系数最大值小于W50, 当k=0.48时, 二者的升力系数最大值几乎重合.而在运动经过升力最大值点后的升力下降期, S75W50的升力大于W50.这与二者在俯仰的不同阶段前缘涡的形态的变化有关, 将在第3部分中重点分析.
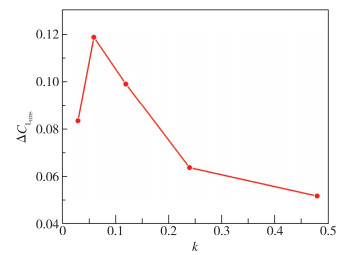
两个模型升力差值的均方根(RMS)随缩减频率的变化如图 10所示.当缩减频率k>0.06时, 升力差值的均方根随缩减频率的增加而减小, 说明随着缩减频率的增加, 两模型升力曲线的差别减小.
|
| 图 10 模型升力差值的均方根(RMS)随缩减频率的变化 Fig.10 Curve of RMS of lift difference of two models with reduced frequency |
这与涡升力在整体升力中的占比减小有关.随着缩减频率的增加, 机翼的俯仰速度增加, 机翼的俯仰线速度对来流产生上洗或下洗作用, 使三角翼在同一时刻的不同流向位置存在不同的等效迎角, 即模型产生了等效弯度.对于S75W50, 前方边条翼部分与俯仰轴的距离较远, 在较大的缩减频率下, 模型等效弯度很大, 等效迎角很小甚至为负, 故此时不会产生边条涡, 或产生的边条涡较弱, 涡升力对整体升力的贡献减小.随着缩减频率的增加, 由等效弯度产生的附加环量力、由加速度产生的附加质量力等非涡力的大小逐渐增加.在双三角翼中, 边条部分的面积仅占双三角翼整体面积的10.6%左右, 边条对等效弯度的作用和附加质量力的影响较小, 故随着缩减频率的增加, S75W50与W50俯仰过程中非定常升力曲线的差别逐渐减小.
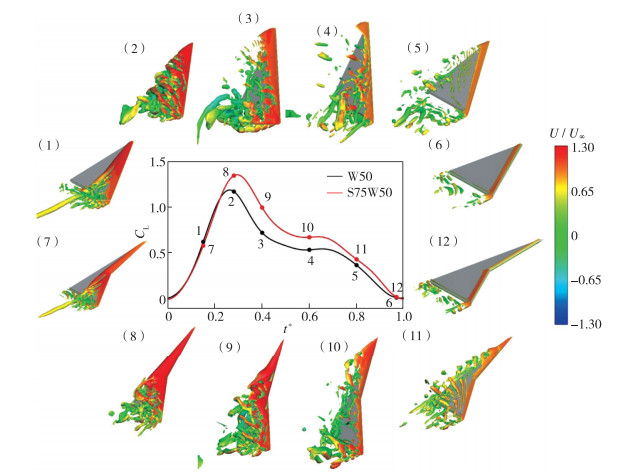
3 CFD模拟流场结果分析 3.1 k=0.06俯仰运动流场结果分析图 11为k=0.06时W50与S75W50的前缘涡对比, 分别选取了W50与S75W50俯仰运动过程中的6个典型时刻的前缘涡形态来对比分析机翼俯仰运动的流动机制.本研究中所用的旋涡识别方法为Q准则, 图中的旋涡由Q=50等值面表示.
|
| 图 11 k=0.06时W50与S75W50的前缘涡对比 Fig.11 Comparison of leading-edge vortices between W50 and S75W50 at k=0.06 |
如图 11中(1)和(7)所示, 在上仰开始阶段t*=0.15处, 也就是升力的上升期中, W50与S75W50都有前缘涡产生, 且前缘涡较集中, 破裂点在后缘附近.由两机翼的拓扑关系可知, 两模型上表面受前缘涡影响的区域占整个机翼上表面面积的比值相同, 故二者的升力系数大小类似.随着机翼继续上仰, 当t*=0.28时, 两模型的升力接近最大值, 此时前缘涡形态如图 11中(2)和(8)所示, W50的前缘涡已经完全破裂, 而S75W50的前缘涡还没有完全破裂, 破裂点位于边条翼与主翼的连接处, 但二者破裂的旋涡还在机翼上表面, 这些离散的涡量也能影响机翼上表面, 产生负压, 故此时的S75W50升力系数较大.当机翼俯仰运动经过升力最大位置后, 升力进入下降期, t*=0.4旋涡形态如图 11中(3)和(9)所示, W50的前缘涡已经完全破裂, 且破碎的旋涡已经流走, 不在机翼表面, S75W50的前缘涡还没有完全破裂, 破裂点继续向翼尖移动, 故此时二者的升力都下降但S75W50的升力较大.
t*=0.6的旋涡如图 11中(4)和(10)所示, 此时机翼运动到最大迎角60°附近, 由图可知此时的前缘涡已经完全破裂, 但此时的运动速度较小, 可认为在此期间的流动为准静态流动, 因此在t*=0.5附近升力曲线存在一段平台期.在t*=0.8附近, 升力曲线又进入下降期, 此时上表面旋涡几乎完全耗散, 仅剩的一些旋涡也距离机翼上表面较远, 此时的下降可认为是纯势流作用, 随着模型迎角的减小, 升力下降.当模型继续下俯, 在t*=0.94时, 升力达到最小值, 此时的旋涡如图 11中(6)和(12)所示, 上表面完全不存在旋涡, 升力近似为0.
综上所述, 在低频俯仰过程中, 两模型升力产生差异的主要原因是旋涡形态不同, S75W50双三角翼模型能产生较强的边条涡, 而W50单三角翼模型产生的前缘涡较弱, 在俯仰运动过程中比双三角翼模型的边条涡更早破裂, 使其升力小于双三角翼.
3.2 k=0.48俯仰运动流场结果分析图 12为k=0.48时W50与S75W50的前缘涡对比.在上仰的开始阶段, t*=0.15时, 如图 12中(1)和(7)所示, 此时W50已经有前缘涡产生, 而S75W50的主翼上有前缘涡产生, 而边条翼上没有前缘涡产生, 此时双三角翼边条的等效迎角很小, 即此时边条翼与水流的相对速度小, 因此并没有前缘涡产生, 故边条不产生额外的涡升力, 甚至对升力有损失作用, 所以此时两模型升力近似.当机翼继续上仰, 达到t*=0.28时, 如图 12中(2)和(8)所示, W50已经产生了较强的前缘涡, 而S75W50在边条上的前缘涡较弱, 可影响的机翼上表面范围小, 因此此时的S75W50升力低于W50升力.当升力进入下降期后, 图 12中(3)和(9)为t*=0.4时前缘涡分布, 此时W50的前缘涡破裂点已经接近前缘, 升力下降, 而S75W50的边条涡还没有破裂, 因此在此期间二者的升力大小逐渐趋近, 直至S75W50的升力超过W50.当t*=0.6时, 如图 12中(4)和(10)所示, W50的前缘涡已经完全破裂, 但S75W50的旋涡还没有完全破裂, 边条上依然存在前缘涡, 故此时S75W50的升力较大.
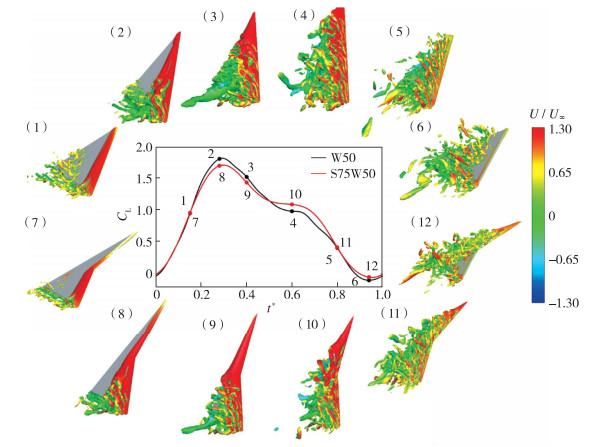
|
| 图 12 k=0.48时W50与S75W50的前缘涡对比 Fig.12 Comparison of leading-edge vortices between W50 and S75W50 at k=0.48 |
当t*=0.8时, 此时两模型处于快速下俯状态, 上表面前缘涡如图 12中(5)和(11)所示, 两模型上表面都存在着复杂但强度较弱的旋涡结构, 此时这些弱涡结构依然会对表面的压力分布产生影响, 使上表面出现负压区, 但对照升力曲线, 此时两模型的升力均快速下降, 与涡结构不符. t*=0.8时两模型上下表面压强分布如图 13所示, 上表面确实受到旋涡的影响存在负压区, 但机翼下表面也存在较大的负压, 此负压在机翼后缘处最大, 沿机翼前缘方向逐渐减弱.此逐渐向机翼前缘扩散的负压区使机翼升力快速下降.
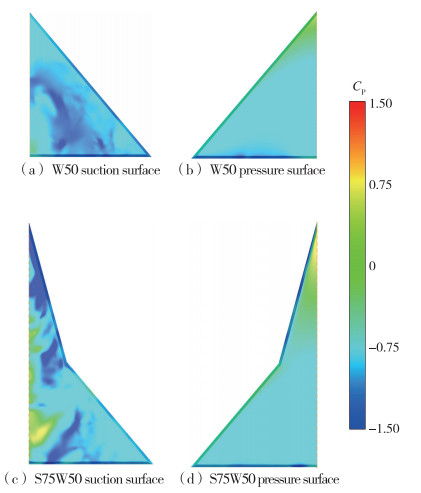
|
| 图 13 k=0.48, t*=0.8时W50与S75W50上下表面压强分布 Fig.13 Pressure distributions of W50 and S75W50 suction and pressure surfaces at k=0.48 and t*=0.8 |
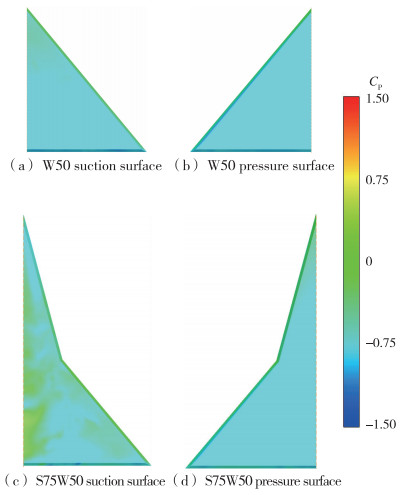
当t*=0.94时, 模型升力达到最小值, 此时机翼上表面的弱涡结构逐渐消散.此时两模型上下表面压强分布如图 14所示, 下表面的负压已经扩散到整个机翼, 模型上下均为负压, 使此时的升力达到最小值.
|
| 图 14 k=0.48, t*=0.94时W50与S75W50上下表面压强分布 Fig.14 Pressure distributions of W50 and S75W50 suction and pressure surfaces at k=0.48 and t*=0.94 |
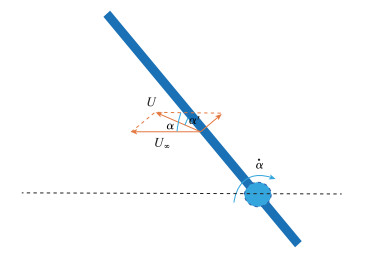
当双三角翼进行连续的俯仰运动时, 运动的机翼会对来流产生上洗或下洗作用, 使机翼的等效迎角发生变化, 如图 15所示.在机翼上仰的过程中, 水流相对于机翼的速度不再是远前方来流速度U∞, 而是U∞与当地转动速度叠加而成的合成速度U, U与模型的夹角即为等效迎角α′.
|
| 图 15 等效迎角示意图 Fig.15 Schematic diagram of equivalent angle of attack |
模型在绕固定转轴旋转时, 其弦向各点的线速度不同, 故各点存在不同的等效迎角, 即三角翼整体存在一个等效弯度.
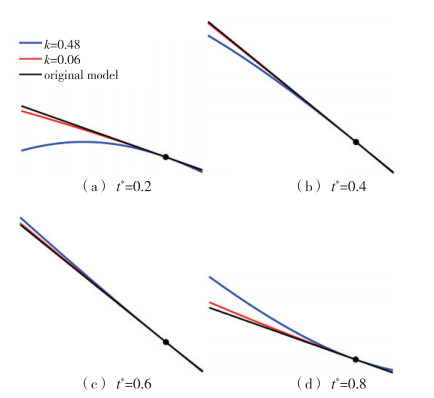
图 16为不同缩减频率下双三角翼在一个运动周期内不同时刻的等效弯度示意图.双三角翼上仰的前期, 如图 16(a)所示, 在较小的缩减频率(k=0.06)下, 双三角翼附加等效弯度后与原模型的差别较小; 但在较大的缩减频率(k=0.48)下, 经变换后的模型与原模型差别较大, 特别是双三角翼前方的边条部分等效迎角很小, 故在较高缩减频率下双三角翼的边条上并没有前缘涡产生, 使双三角翼模型与单三角翼模型的升力近似相等.双三角翼上仰的后期, 如图 16(b)所示, 两个缩减频率下的等效弯度都较小, 此时的升力主要由旋涡结构决定, 此过程中前缘涡逐渐破裂, 使两模型的升力均进入快速下降期.
|
| 图 16 不同时刻双三角翼等效弯度示意图 Fig.16 Schematic diagram of equivalent bending of double-delta wing at different times |
双三角翼下俯的开始阶段, 如图 16(c)所示, 此时的等效弯度影响较小, 三角翼升力主要由涡升力决定.而到了下俯的后期, 高缩减频率下等效弯度的影响逐渐增大, 等效弯度的作用成为双三角翼升力的决定性因素, 所以双三角翼和单三角翼的升力又趋于一致.
综上所述, 在较低的缩减频率下, 由等效弯度而产生的附加环量力较小, 影响升力的主要因素为前缘涡, 双三角翼的前缘涡较强, 故低频下双三角翼的升力系数较大.在较高的缩减频率下, 等效弯度产生的附加环量力较大, 特别是在一个俯仰周期的开始和结束阶段, 等效弯度不仅能直接产生较强的环量力, 还能影响前缘涡的产生和发展, 使双三角翼边条的作用减弱, 故在较高的缩减频率下双三角翼和单三角翼的升力系数差别较小.
4 结论(1) S75W50双三角翼在进行俯仰运动时, 其气动力会产生迟滞环, 且随着缩减频率的增加, 迟滞环增大.
(2) 当缩减频率较小时, S75W50双三角翼在迎角较小时升力迟滞环会收缩成近似一条线, 即在模型静态、上仰和下俯时的升力相同.
(3) 随着缩减频率的增加, W50与S75W50的升力曲线趋于一致.
(4) 在较低缩减频率下, 如k=0.06, 机翼升力与前缘涡形态密切相关, 即前缘涡是影响升力的主要因素.
(5) 在较高缩减频率下, 如k=0.48, 机翼前缘涡不再是影响升力的主要因素, 由机翼等效弯度产生的附加环量力也对升力有很大贡献.
| [1] |
Zagainov G I. High maneuverability. Theory and practice[R]. AIAA 93-4737, 1993.
|
| [2] |
Mahon M C, Wentz W H. An experimental investigation of the flow fields about delta and double-delta wings at low speeds[R]. NASA-CR-521, 1966.
|
| [3] |
Mahon M C, Wentz W H. Further experimental investigations of delta and double-delta wing flow fields at low speeds[R]. NGR-17-003-003, 1967.
|
| [4] |
Hoeijmakers H W, Vaatstra W, Verhaagen N G. Vortex flow over delta and double-delta wings[J]. Journal of Aircraft, 1983, 20(9): 825-832. |
| [5] |
Zhang X, Wang Z J, Gursul I. Interaction of multiple vortices over a double delta wing[J]. Aerospace Science and Technology, 2016, 48: 291-307. |
| [6] |
Den Boer R G, Cunningham A M. Low-speed unsteady aerodynamics of a pitching straked wing at high incidence-Part I:test program[J]. Journal of Aircraft, 1990, 27(1): 23-30. DOI:10.2514/3.56824 |
| [7] |
Den Boer R G, Unningham A M. Low-speed unsteady aerodynamics of a pitching straked wing at high incidence-Part II:Harmonic analysis[J]. Journal of Aircraft, 1990, 27(1): 31-41. DOI:10.2514/3.45893 |
| [8] |
Hebbar S, Platzer M A, Li F H. A visualization study of the vortical flow over a double-delta wing in dynamic motion[R]. AIAA 1993-3425, 1993.
|
| [9] |
Grismer D S, Nelson R C. Double-delta-wing aerody-namics for pitching motions with and without sideslip[J]. Journal of Aircraft, 1995, 32(6): 1303-1311. |
| [10] |
Myose R, Lee B K, Hayashibara S, et al. An experimental study of the breakdown of leading-edge vortices on dia-mond, cropped, delta, and double delta wings during dynamic pitching[R]. AIAA 97-1930, 1997.
|
| [11] |
Ericsson L E. Vortex characteristics of pitching double-delta wings[J]. Journal of Aircraft, 1999, 36(2): 349-356. |
| [12] |
Liu J, Sun H S, Liu Z T, et al. Numerical investigation of unsteady vortex breakdown past 80°/65° double-delta wing[J]. Chinese Journal of Aeronautics, 2014, 27(3): 521-530. DOI:10.1016/j.cja.2014.04.018 |
| [13] |
Liu J, Luo K Y, Sun H S, et al. Dynamic response of vortex breakdown flows to a pitching double-delta wing[J]. Aerospace Science and Technology, 2017, 72: 564-577. |
| [14] |
Spalart P R, Deck S, Shur M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181-195. |




