计算成像技术[1-3]作为光学成像技术的一个重要分支, 以其非侵入性、高分辨率等优势, 被广泛应用于生物医学、材料科学、航空航天等领域[4-5].层析成像技术是计算成像的一个典型例子, 其原理是基于视线法(line of sight, LOS)对目标函数场进行重建[6].在燃烧诊断领域, 层析成像得到了深入而广泛的研究[4], 而其中吸收光谱层析(tomographic absorption spectroscopy, TAS)技术以其用途广泛、环境适应性强、设备结构简单、可实现温度及物质浓度场同时重建等优势, 成为了燃烧诊断中常采用的手段与近年来相关研究的热点[7-9].
在TAS技术的应用中, 求解基于LOS的辐射反问题是实现目标函数场重构的关键, 而TAS中的反问题往往具有病态性, 因此反演算法的选择对重建的效果有着显著的影响[10].用于TAS的反演算法多发展自医学成像、工业过程控制等领域, 主要包括代数重建(algebraic reconstruction technique, ART)算法[11], Landweber算法[12]、最大似然期望最大化(maximum likelihood expectation maximiza-tion, MLEM)算法[13]、最小二乘分解(least square QR decomposition, LSQR)算法[14]、联合代数重建(simultaneous algebraic reconstruction technique, SART)算法[15]等.目前针对上述算法, 已有系统的研究, 该类算法的应用虽已近成熟, 但仍存在对噪声敏感、精度受火焰参数影响较大等问题[10], 仍有进一步进行研究与改进的必要.
先验条件包含了待求解函数场已知的特性, 引入先验条件的约束对层析反演问题的病态性有一定的缓解作用[16].在层析反演问题的研究中, 平滑性、稀疏性等先验条件有较广泛的应用, 如Tikhonov正则化[17], 全变分凸集投影(total variance-projections onto convex sets, TV-POCS)算法[18]等, 分别将重建目标场的连续性、全变分作为正则化的目标函数, 利用先验条件在原反演问题中添加约束, 以获得物理上更加真实的解.除上述算法外, 在迭代反演算法中引入超限化进行改进也是结合先验条件进行反演求解的一种代表性方法.这种方法由Butnariu等于2007年提出, 以解决临床医学中成像技术的大规模约束优化问题[19].超限化算法的思路是在传统的迭代过程中加入扰动, 使此迭代序列收敛到先验条件约束下的一个近似最优解. ART算法和MLEM算法是TAS反演的常用算法, 目前对ART算法的超限化[20-22]及期望最大化(expectation maximization, EM)算法的超限化[23-25]已有了颇为深入的研究, 并在CT图象重建、医学成像等领域有着广泛的应用, 但尚未应用在TAS技术中.鉴于ART算法和MLEM算法在TAS反演中的良好性能, 以及其超限化在其他领域中的优秀表现, 本文选择这两种算法进行超限化研究.
本文通过计算机仿真, 引入超限化思想对现有的层析反演算法进行了改进, 并对其在TAS技术中的应用进行了模拟, 就相关结果作出了讨论.在仿真中, 研究了超限化算法对两种典型火焰场的重建效果, 并就不同火焰场适合采用的先验条件进行了讨论.对比了ART, MLEM两种常用的层析反演算法及其超限化算法的性能及其抑制噪声误差的能力.
1 原理及算法介绍 1.1 TAS原理关于TAS的原理已有较为详细的介绍[15, 26-27].当一束固定波长的激光穿过目标气体时, 其光强将会因吸收而衰减.对于一个各项参数均匀分布的区域, 当激光在此区域中穿过长度为L时, 入射光强I0与透射光强It之间的关系可由Beer-Lambert定律表示为[10]
| $ I_{0} / I_{\rm t}=\exp (S(T, \lambda) \cdot P \cdot L \cdot C \cdot \phi(\lambda, T, C)) $ | (1) |
式中, T为温度; λ为激光波长; S为吸收谱线强度; 为温度和波长的函数; P为压强; C为目标物质浓度; ϕ为线型函数, 与波长、温度、浓度有关.
公式(1)可进一步简化, 写成如下的形式
| $ p=-\ln \left(I_{\rm t} / I_{0}\right)=x(\lambda) \cdot L $ | (2) |
式中, p为当地的吸收强度, x为吸收系数.求得x(λ), 即可利用谱线强度、线型函数等关系式得到当地的温度、浓度等参数.因此, TAS反演中的主要问题即是求得吸收系数x的分布.
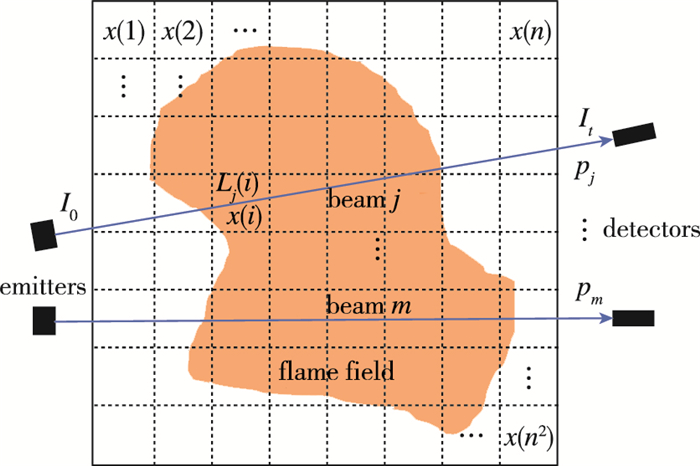
如图 1所示, 将所测量的二维火焰区域离散划分为n × n的网格, 只要网格尺寸足够小, 即可假设每个网格中的温度、浓度等参数是均匀分布的.设共有m条光线穿过火焰区域, 则其中第j条光线的吸收强度p(j)可表示为
| $ p(j)=\int x(\lambda, L) \mathrm{d} L \approx \sum_{i=1}^{n^{2}} x(i) L_{j}(i) $ | (3) |
|
| 图 1 二维火焰场TAS系统示意图 Fig.1 Illustration of TAS system in a two-dimensional flame field |
式中, x(i)为第i个网格的吸收系数, Lj(i)表示第j条光线穿过第i个网格的长度.公式(3)可写成矩阵的形式
| $ \boldsymbol{p}=\boldsymbol{L}\cdot \boldsymbol{x} $ | (4) |
式中, p∈Rm, x∈Rn2, L∈Rm×n2称权重系数矩阵, 可根据光线排布方式算出.在TAS中, p为测量值, 在已知p与L的情况下求x即为反演的过程, 须采用合适的算法进行求解.
1.2 反演算法简介 1.2.1 ART算法ART算法是层析成像反演中应用最广泛的迭代方法之一, 最初由Kaczmarz提出[27], Gordon等在1970年将其应用在层析反演中[11].其迭代过程可表示为
| $ \boldsymbol{x}^{(k+1, i)}=\boldsymbol{x}^{(k, i)}-\lambda_{\mathrm{ART}} \frac{\boldsymbol{L}_{i} \boldsymbol{x}^{(k, i)}-p_{i}}{\left\|\boldsymbol{L}_{i}\right\|_{2}^{2}} \boldsymbol{L}_{i}^{\mathrm{T}} $ |
其中, k表示第k次迭代, i在每次迭代中由1~m依次增加, Li表示权重矩阵的第i行, pi表示右项中的第i个元素, λART∈(0, 2)为松弛因子, 影响迭代的收敛速度.一般来说, 较大的松弛因子可以加快收敛速度, 但使得结果更容易发散.在本文的研究中, 根据经验将λART的值设置为0.7.
ART算法作为迭代算法, 须设置终止条件以结束迭代.将两次迭代得到x的相对差值ε作为迭代终止的判定指标.当ε < 10-4, 或迭代次数超过500次时, 迭代终止, 此时得到的x为反演结果.终止条件以公式的形式可写为
| $ \varepsilon=\left\|\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}\right\| /\left\|\boldsymbol{x}^{(k)}\right\| <10^{-4} $ |
此外, 迭代的初始值x(0)可任意选取.本文取零向量作为迭代的初始值.
1.2.2 MLEM算法MLEM算法首先由Dempster等在1977年提出[13], 自20世纪80年代以来, 被广泛应用于层析成像分析[28-29].在不考虑光线宽度的情况下, 其原理用公式可表示为[28]
| $ x_{j}^{(k+1)}=\frac{\sum_{i=1}^{m} L_{i j} \frac{p_{i}}{\tilde{p}_{i}}}{\sum_{i=1}^{m} L_{i j}} x_{j}^{(k)} $ |
式中, k表示迭代次数, j表示x(k)向量中的第j个元素, 在每次迭代中从1~n2依次枚举, i表示权重矩阵的第i行,
| $ \tilde{p}_{i}=\sum_{j=1}^{n^{2}} L_{i j} x_{j}^{(k)} $ |
MLEM算法对初始值有要求.迭代的初始值为
| $ x_{j}^{(0)}=\frac{\sum_{i=1}^{m} \bar{p}_{l}}{c_{j}} $ |
式中, cj为经过第j个网格的光线数目,
| $ \bar{p}_{l}=\frac{p_{i}}{\sum_{j=1}^{n^{2}} L_{i j}} $ |
对于终止条件的定义, MLEM的迭代终止条件与前文所言的ART算法相同, 此处不再赘述.
1.3 超限化算法超限化算法是一种有效的求解大规模约束优化问题的算法[30].该优化问题的模型可描述为
| $ \text{min}(\varphi (\boldsymbol{x}))\quad \text{ s}\text{.t}\text{. }\quad \boldsymbol{L}\cdot \boldsymbol{x}=\boldsymbol{p} $ |
其中, φ(x)为目标约束函数, 采用两种目标函数:平滑性, 即Tikhonov正则化模型; 以及全变分(total variance, TV)正则化模型.两目标函数分别定义为[24]
| $ \operatorname{Tik}(x)=\sum\limits_{r \in R}\left(x_{r}-\frac{1}{8} \sum\limits_{l \in M_{r}} x_{l}\right) $ |
其中, R为火焰场中不处于网格最边缘一圈的点集, Mr为R中一点r周围的8个点构成的点集.
| $ TV(x)=\sum\limits_{c\in C}{\sqrt{{{\left( {{x}_{c}}-{{x}_{c\text{r}}} \right)}^{2}}+{{\left( {{x}_{c}}-{{x}_{c\text{h}}} \right)}^{2}}}} $ |
其中, C为不处于网格最右一列和最下一行的点集, cr, ch为其中一点c右侧与上方的点.
超限化算法的步骤包括[19]:第1步, 对当前迭代结果在目标函数φ(x)的下降方向上添加扰动, 并验证该扰动是否使目标函数下降, 若不是, 则减小扰动直到目标函数下降; 第2步, 对加扰动后的结果进行迭代, 得到的迭代结果需要使残差下降, 否则减少扰动直到满足条件.之后的步骤与ART算法相同, 重复上述的迭代过程直到满足迭代的终止条件.
| 下载CSV 表 1 算法伪码 Tab.1 Superiorization algorithm |
其中, k为迭代次数, β为任意正实数, 0 < γ < 1, v为目标函数下降方向上的扰动, res为残差, 定义为
| $ res=\sqrt{{{\left( \frac{{{p}_{i}}-\left\langle {{\boldsymbol{L}}_{i}}, \boldsymbol{x} \right\rangle }{{{p}_{i}}} \right)}^{2}}} $ |
一般来说, 残差越小说明越接近方程组的解.
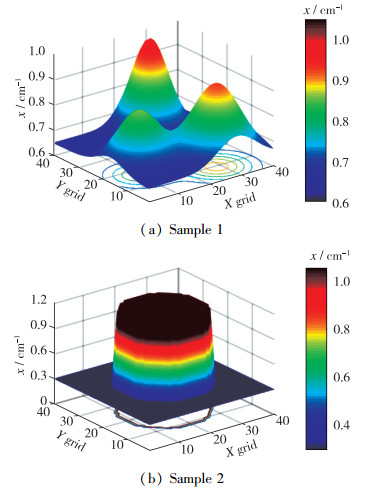
2 仿真方案设计 2.1 火焰样例仿真中采用的火焰场如图 2所示.模拟了两种代表性的二维火焰场, 在样例中以吸收系数的分布反映火焰场的特征. 图 2中, 水平两坐标轴分别表示X, Y两方向的网格; 纵轴表示吸收系数x, 单位为cm-1.火焰场1为3个不同位置、不同形状的二维Gauss分布的叠加, 用以模拟实际燃烧中火焰的非对称性; 火焰场2为柱状分布, 用以模拟分段平滑的火焰场, 如McKenna火焰[31]等.
|
| 图 2 火焰样例 Fig.2 Samples of flame |
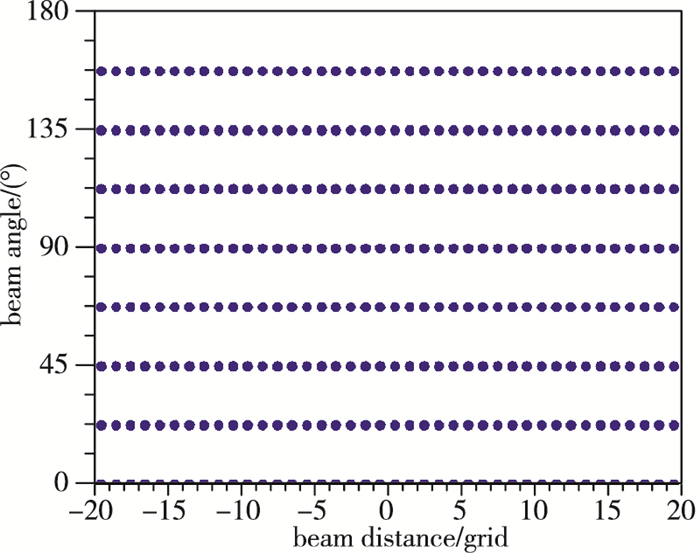
光线排布的Radon图[32-33]如图 3所示.在40×40的网格分割的火焰场中, 在若干个平均分布的方向上均匀排布光线, 每个方向排布40条.投影方向个数设置为4~24个不等, 以便研究其对重建精度的影响. 图 3所示情况为8个角度的光线排布.
|
| 图 3 光线排布Radon图 Fig.3 Radon plot of beam arrangement |
火焰重建仿真包括以下4个步骤:第1步, 通过已知火焰场分布xact和权重矩阵L计算出真实的吸收强度阵列pact; 第2步, 为模拟实际的测量情况, 在吸收强度的真实值上加上随机噪声, 得到吸收强度的测量值pmes; 第3步, 根据吸收强度的测量值pmes和权重矩阵L, 分别通过加入了超限化的反演算法和未加超限化的该算法重建得到火焰场xrec, 并记录重建所用的时间及迭代次数; 第4步, 将不同噪声下各算法得到的火焰场重建值进行对比, 分析模拟结果.
噪声的添加方法为在吸收强度的真实值上加上一个均匀分布的随机项, 并将其上限定义为噪声的强度.噪声的详细定义为
| $ p_{\operatorname{mes}}(j)=p_{\mathrm{act}}(j) \cdot(1+u \% \cdot r d) $ |
pmes(j)以及pact(j)分别为第j条光线吸收强度的测量值与真实值, u%为噪声水平, rd为(-1, 1)区间上均匀分布的随机数.对0.5%~5%水平的噪声的影响进行了研究.结果分析中, 重建结果的误差定义为
| $ \text { error }=\sqrt{\frac{\left\|\boldsymbol{x}_{\mathrm{rec}}-\boldsymbol{x}_{\mathrm{act}}\right\|}{\left\|\boldsymbol{x}_{\mathrm{act}}\right\|}} $ |
迭代的次数上限、收敛条件等采用1.2, 1.3节中的定义及取值.
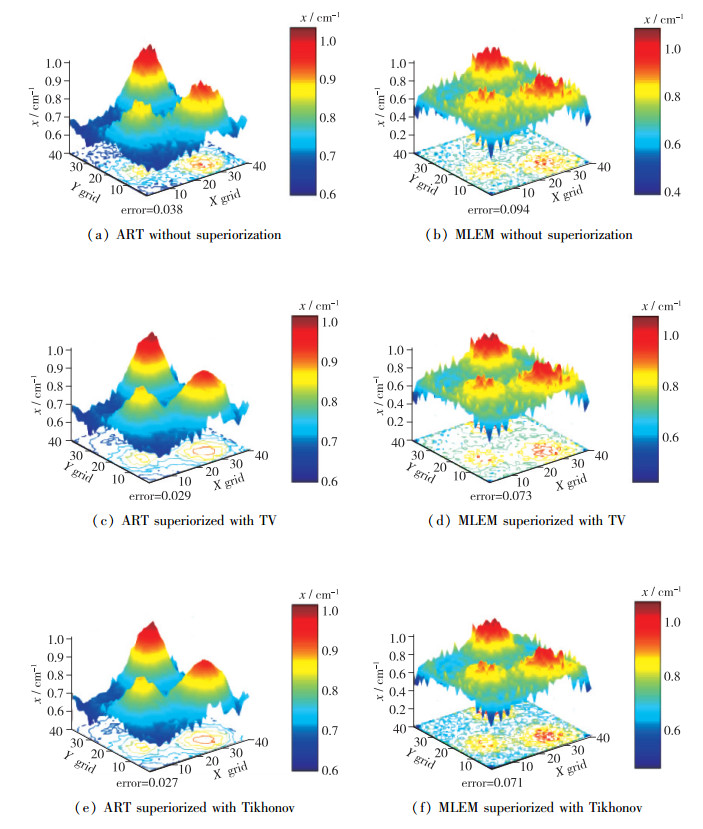
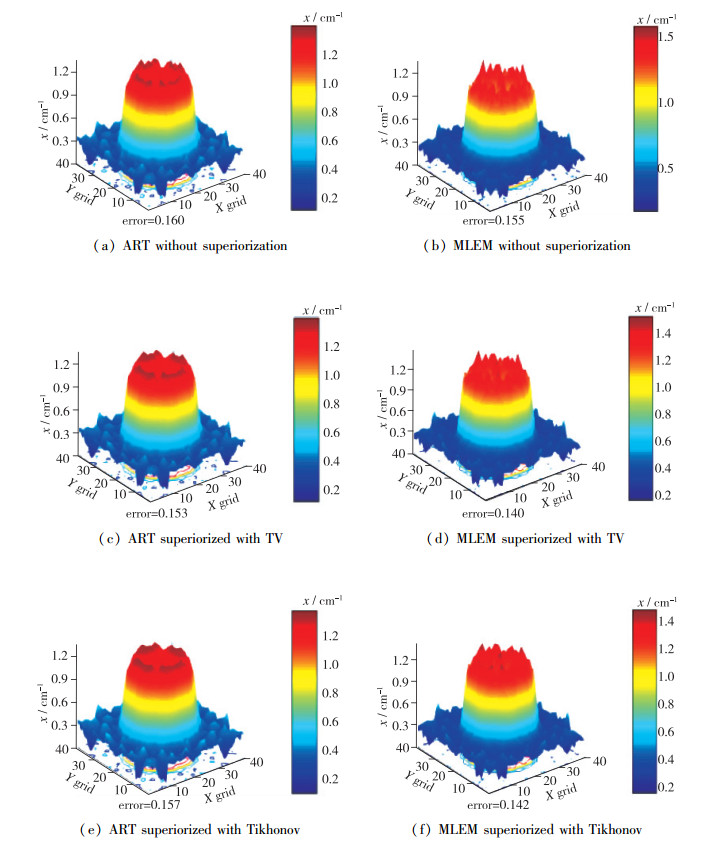
3 仿真结果及分析 3.1 重建结果在1.0%的噪声条件下, 利用8个方向的投影对两火焰场进行了仿真重建, 各算法的结果分别如图 4, 5所示.其中, 水平两坐标轴分别表示X, Y两方向的网格; 纵轴表示吸收系数x, 单位为cm-1.
|
| 图 4 火焰场1重建结果 Fig.4 Reconstruction results of flame field 1 |
|
| 图 5 火焰场2重建结果 Fig.5 Reconstruction results of flams field 2 |
从重建结果中可以看出, 在上述的模拟条件下, 对于火焰场1, ART系的重建算法较MLEM算法有着较好的重建效果; 而超限化算法的引入减小了重建误差, 对于两种算法的重建效果都有着一定的提升; 且采用Tikhonov正则化比采用全变分作为目标函数有着更好的效果.对于火焰场2, 几种算法都有着较大的重建误差, 而MLEM系算法的重建效果要稍好; 超限化的引入同样有着降低误差的效果; 在火焰场2的重建中, 使用全变分作为目标函数有着更好的效果.
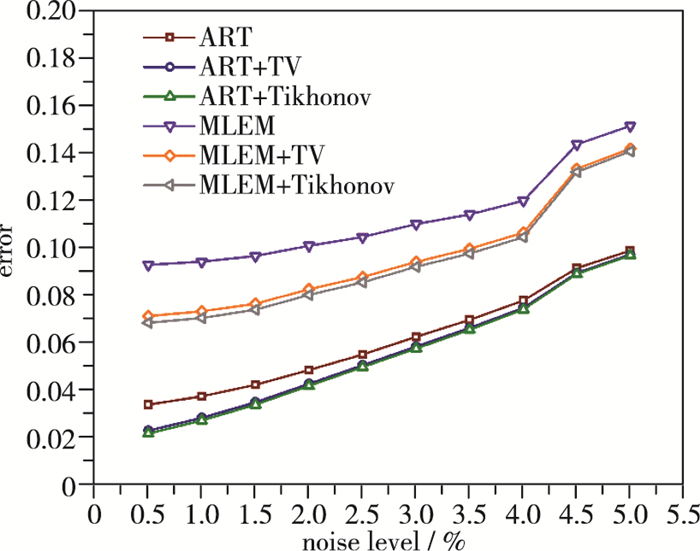
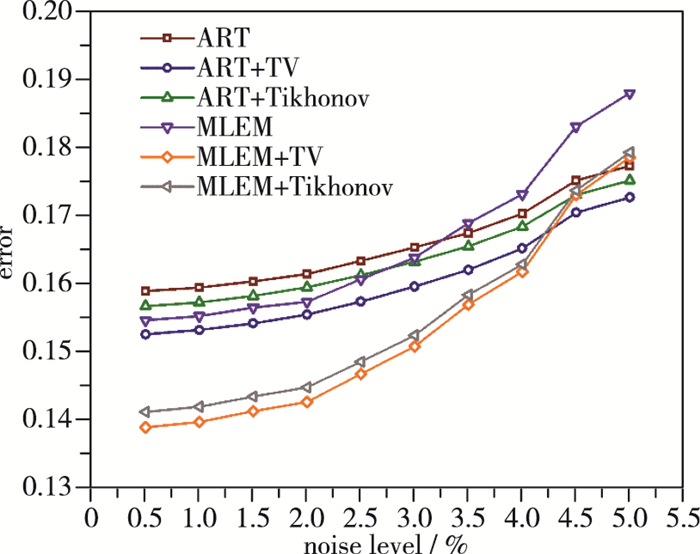
3.2 噪声的影响在实际的测量中, 测量噪声对重建结果往往会有着较大的影响.因此对不同强度噪声下超限化算法的效果进行测试是很有必要的.仿真采用8个投影方向, 噪声水平为0.5%~5%.结果如图 6, 7所示.
|
| 图 6 不同噪声条件下对火焰场1重建误差 Fig.6 Reconstruction errors of flame field 1 under different noise levels |
|
| 图 7 不同噪声条件下对火焰场2重建误差 Fig.7 Reconstruction errors of flame field 2 under different noise levels |
由图 6可知, 对于火焰场1, 在不同噪声条件下, 加入了超限化的算法都比相应的层析算法有着更小的重建误差, 而超限化的引入对MLEM算法性能的提升比ART算法更加明显.然而, 注意到噪声较高时超限化算法降低误差的效果趋于不明显, 可以认为超限化的引入并没有提高算法抵抗噪声能力的效果.
对于火焰场2, 可以由图 7得到相似的结论.虽然引入超限化后, ART算法与MLEM算法的重建误差都有所下降, 但并不能认为其抵抗噪声的能力提高了.从图中也可看出, 在引入超限化前后, MLEM算法对于噪声都更为敏感.
3.3 光线数的影响在TAS中, 测量光线蕴含着火焰场的信息, 每条光线都对应着反问题中线性方程组的一个方程.光线的排布、数目对重建的效果、效率、资源消耗等有着重要的影响.在本文的研究中, 光线数与投影的方向数成正比, 更多的投影方向往往能更加全面地反映火焰场的信息, 但需要更多的计算资源.因此, 对不同投影数下超限化算法的效果进行了研究.仿真采用1%的随机噪声, 投影数为4~24个方向不等, 绕火焰场均匀分布.
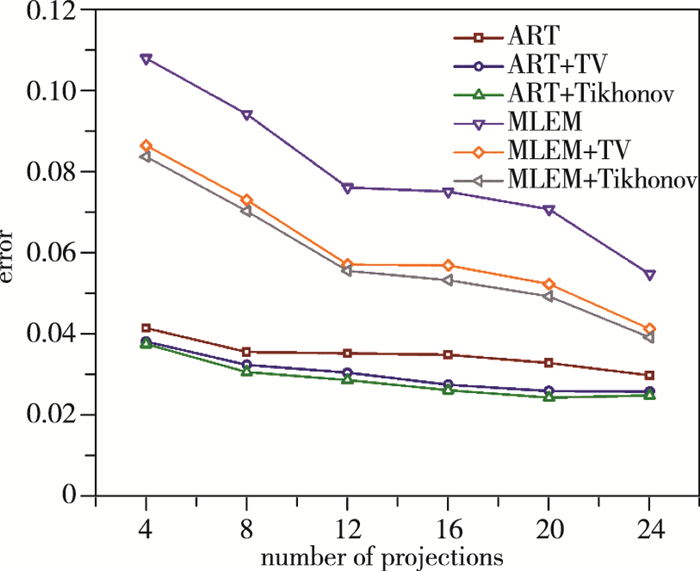
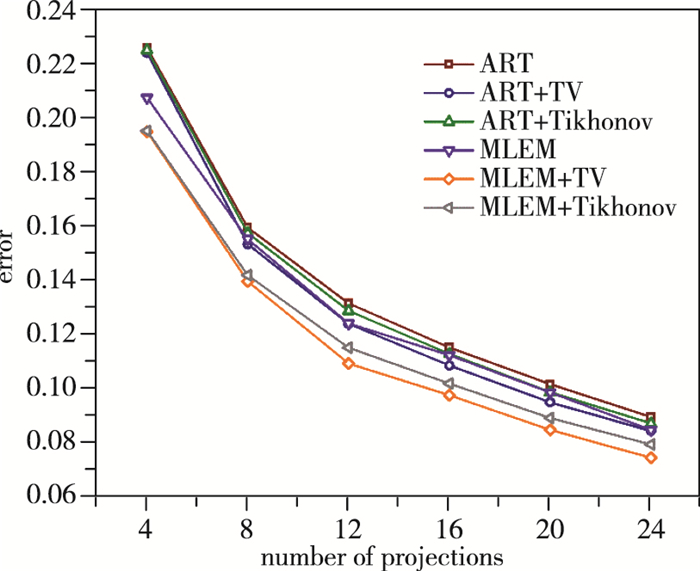
由图 8, 9可知, 对于两火焰场, 更多的投影方向数往往会得到更小的重建误差.对于火焰场2, 可以认为在光线数更多时, 引入超限化能给重建结果带来更加明显的提升.从火焰场1的重建结果中, 则难以看出超限化的效果与投影数有着明显关系.
|
| 图 8 不同投影数下对火焰场1重建误差 Fig.8 Reconstruction errors of flame field 1 withdifferent projection numbers |
|
| 图 9 不同投影数下对火焰场2重建误差 Fig.9 Reconstruction errors of flame field 2 withdifferent projection numbers |
在医学成像中, 超限化算法除提高成像质量外, 也有提高重建速度的作用[30].同样, 在TAS中, 提高计算的速度和效率也是很重要的.因此, 对超限化算法对计算效率的影响进行了研究.研究手段包括比较各算法引入超限化前后重建误差随迭代次数的收敛速度、统计迭代收敛时所需的迭代次数以及时间等.仿真实验在1%的噪声、8个投影方向的条件下进行.
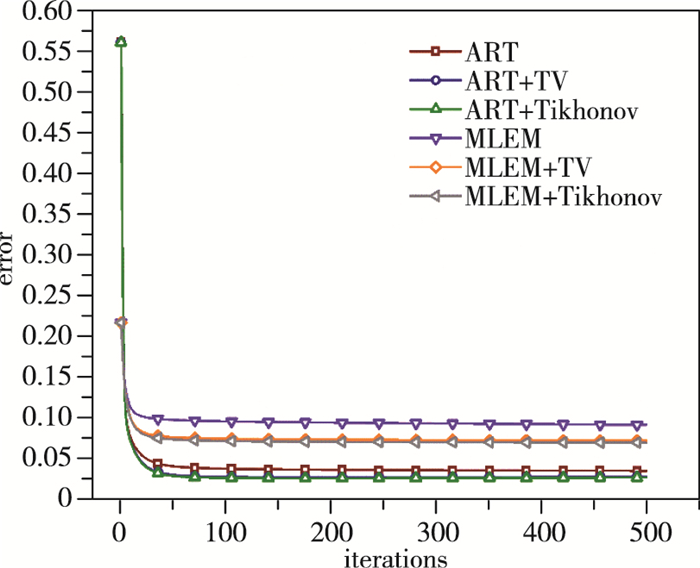
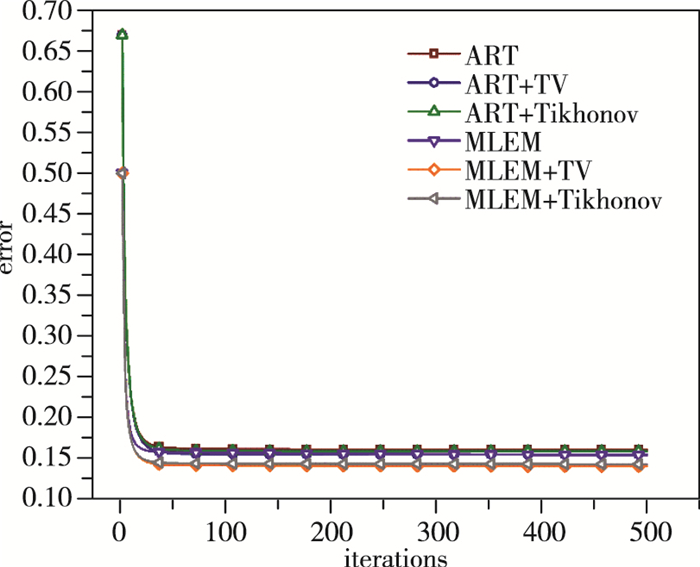
由图 10, 11可知, 对于两火焰场, 在任意的迭代次数时, 引入超限化的算法都相应地有着更小的重建误差, 但超限化算法的重建误差随迭代数并未明显表现出更快的下降趋势.因此并不能看出在此条件下超限化能够加快收敛速度.
|
| 图 10 火焰场1重建误差随迭代变化曲线 Fig.10 Reconstruction errors of flame field 1 with iteration processes |
|
| 图 11 火焰场2重建误差随迭代变化曲线 Fig.11 Reconstruction errors of flame field 2 with iteration processes |
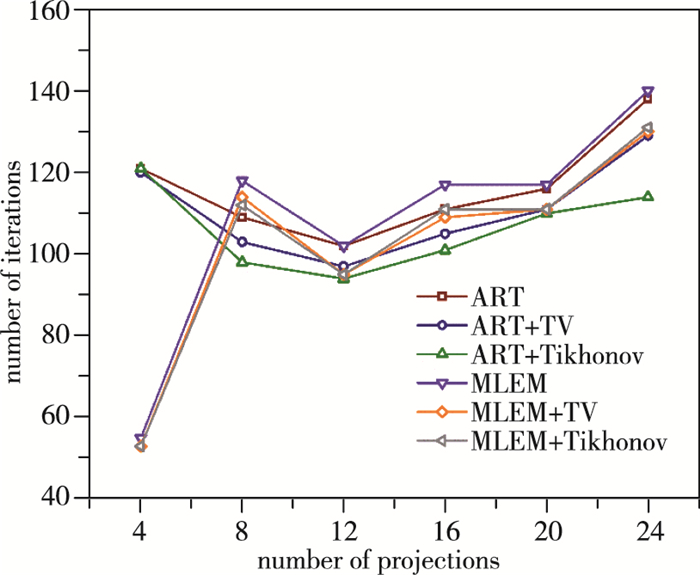
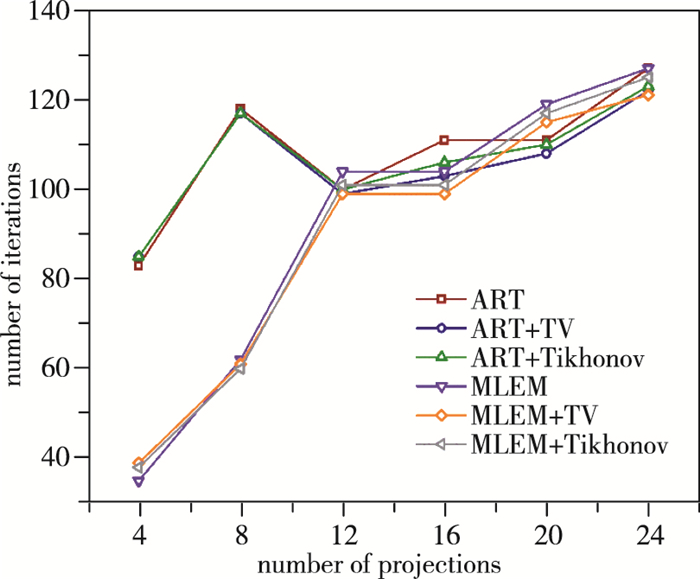
由图 12, 13可知, 对于两火焰场, 除投影数为4以外, 超限化算法都相应地在更小的迭代数时趋于收敛, 且投影数越多时差距越明显.投影数为4时, 引入超限化前后收敛所需的迭代次数差距也不大, 因此可以认为超限化有着加快收敛速度的作用.对于火焰场1, 采用Tikhonov正则化作为目标函数会有着更快的收敛速度; 而对于火焰场2, 采用全变分作为正则项有着更快的收敛速度.这也与重建误差的结果相同.
|
| 图 12 不同投影数下火焰场1重建收敛所需迭代次数 Fig.12 Number of iterations before convergence for flame field 1 with different projection numbers |
|
| 图 13 不同投影数下火焰场2重建收敛所需迭代次数 Fig.13 Number of iterations before convergence for flame field 2 with different projection numbers |
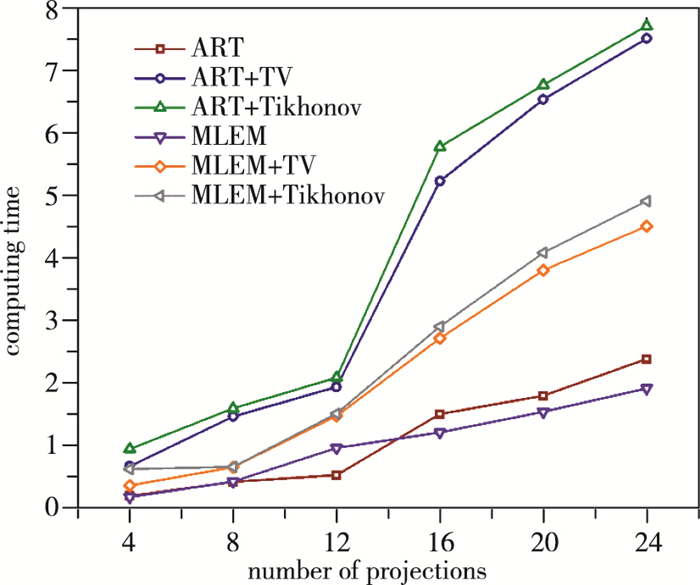
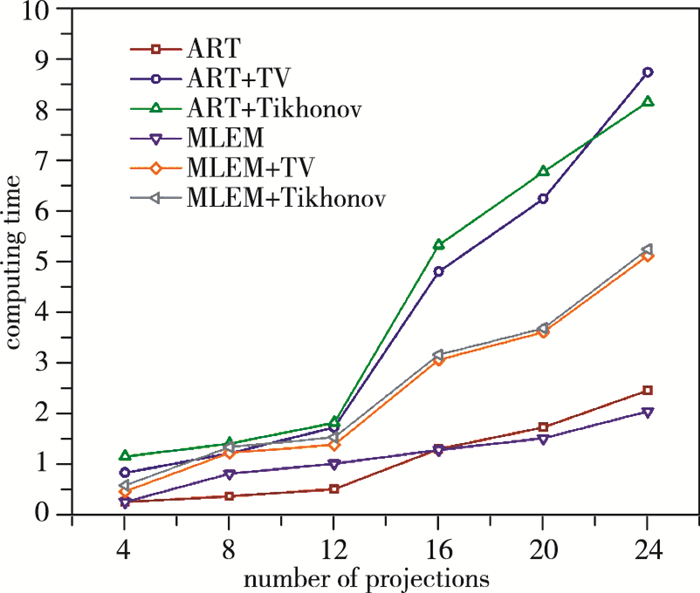
由图 14, 15可知, 对于两火焰场, 一方面更多的投影方向数意味着更长的计算时间; 另一方面, 对于相同的投影数, 超限化算法都将需要更长的计算时间.这是因为虽然超限化算法收敛所需的迭代数较少, 但迭代过程较复杂, 每一步迭代所需的时间较长.此外, 对于两火焰场, 全变分作为目标函数往往计算速度比Tikhonov正则化要快.
|
| 图 14 不同投影数下火焰场1重建计算时间 Fig.14 Computing times for flame field 1 with different projection numbers |
|
| 图 15 不同投影数下火焰场2重建计算时间 Fig.15 Computing times for flame field 2 with different projection numbers |
本文通过对两种典型火焰场TAS重建的计算机仿真, 对比了不同层析反演算法、不同目标函数下超限化算法的重建效果, 模拟了测量噪声、测量光线数等条件对重建的影响, 研究了超限化算法的计算效率, 验证了TAS中超限化对ART算法、MLEM算法的改进作用.结论如下:
(1) 引入超限化对层析反演算法的重建精度有一定的提升作用;
(2) 对于不同的火焰场, 采用合适的先验条件作为目标函数, 才能得到更好的重建效果, 如Tikhonov正则化函数适合整体平滑的火焰场, 全变分则适合分段光滑的火焰场;
(3) 引入超限化并不能增强层析反演算法抵抗测量噪声的能力;
(4) 超限化虽然能加快迭代的收敛速度, 但计算速度较慢.即在相同的收敛条件下, 加入了超限化的算法达到收敛需要的迭代次数更少, 但需要的时间更长.上述效应在测量光线数较多时更加明显.
致谢 本研究得到了国家自然科学基金(51706141, 51906122)的资助, 在此表示感谢.| [1] |
Sun J, Xu C L, Zhang B, et al. Three-dimensional temperature field measurement of flame using a single light field camera[J]. Optics Express, 2016, 24(2): 1118-1132. |
| [2] |
Meyer T R, Halls B R, Jiang N B, et al. High-speed, three-dimensional tomographic laser-induced incandes-cence imaging of soot volume fraction in turbulent flames[J]. Optics Express, 2016, 24(26): 29547-29555. |
| [3] |
Halls B R, Thul D J, Michaelis D, et al. Single-shot, volumetrically illuminated, three-dimensional, tomogra-phic laser-induced-fluorescence imaging in a gaseous free jet[J]. Optics Express, 2016, 24(9): 10040-10049. |
| [4] |
Cai W W, Kaminski C F. Tomographic absorption spectroscopy for the study of gas dynamics and reactive flow[J]. Progress in Energy and Combustion Science, 2017, 59: 1-31. |
| [5] |
Herman G T. Fundamentals of computerized tomography:Image reconstruction from projection[M]. 2nd ed. London: Springer, 2009: 1-26.
|
| [6] |
Herman G T. Image reconstruction from projections[M]. Berlin: Springer-Verlag, 1979: 64-68.
|
| [7] |
Tsekenis S, Tait N, McCann H. Spatially resolved and observer-free experimental quantification of spatial resolution in tomographic images[J]. Review of Scientific Instruments, 2015, 86(3): 035104. |
| [8] |
Cai W W, Kaminski C F. A tomographic technique for the simultaneous imaging of temperature, chemical species, and pressure in reactive flows using absorption spectroscopy with frequency-agile lasers[J]. Applied Physics Letters, 2014, 104(3): 034101. |
| [9] |
李可.基于吸收光谱技术的燃烧场温度与浓度层析成像方法研究[D].南京: 东南大学, 2016. Li K. Study on tomography of temperature and concentration in combustion based on absorption spectrum techno-logy[D]. Nanjing: Southeast University, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10286-1016328901.htm |
| [10] |
Yu T, Cai W W. Benchmark evaluation of inversion algorithms for tomographic absorption spectroscopy[J]. Applied Optics, 2017, 56(8): 2183-2194. |
| [11] |
Gordon R, Bender R, Herman G T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography[J]. Journal of Theoretical Biology, 1970, 29(3): 471-481. |
| [12] |
Landweber L. An iteration formula for Fredholm integral equations of the first kind[J]. American Journal of Mathematics, 1951, 73(3): 615-624. |
| [13] |
Dempster A P, Laird N M, Rubin D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society. Series B, 1977, 39(1): 1-38. |
| [14] |
Paige C C, Saunders M A. LSQR:an algorithm for sparse linear equations and sparse least squares[J]. ACM Transactions on Mathematical Software, 1982, 8(1): 43-71. |
| [15] |
Andersen A H, Kak A C. Simultaneous algebraic reconstruction technique (SART):a superior implementation of the ART algorithm[J]. Ultrasonic Imaging, 1984, 6(1): 81-94. |
| [16] |
Daun K J, Grauer S J, Hadwin P J. Chemical species tomography of turbulent flows:Discrete ill-posed and rank deficient problems and the use of prior information[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2016, 172: 58-74. |
| [17] |
Tikhonov A N. Inverse problems in heat conduction[J]. Journal of Engineering Physics, 1975, 29(1): 816-820. |
| [18] |
Sidky E Y, Kao C M, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT[J]. Journal of X-Ray Science and Technology, 2006, 14(2): 119-139. |
| [19] |
Butnariu D, Davidi R, Herman G T, et al. Stable convergence behavior under summable perturbations of a class of projection methods for convex feasibility and optimization problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 540-547. |
| [20] |
Censor Y, Davidi R, Herman G T. Perturbation resilience and superiorization of iterative algorithms[J]. Inverse Problems, 2010, 26(6): 065008. |
| [21] |
Davidi R, Herman G T, Censor Y. Perturbation-resilient block-iterative projection methods with application to image reconstruction from projections[J]. International Transactions in Operational Research, 2009, 16(4): 505-524. |
| [22] |
Nikazad T, Davidi R, Herman G T. Accelerated perturbation-resilient block-iterative projection methods with application to image reconstruction[J]. Inverse Problems, 2012, 28(3): 035005. |
| [23] |
Luo S S, Zhou T. Superiorization of EM algorithm and its application in single-photon emission computed tomography (SPECT)[J]. Inverse Problems & Imaging, 2014, 8(1): 223-246. |
| [24] |
Garduno E, Herman G T. Superiorization of the ML-EM algorithm[J]. IEEE Transactions on Nuclear Science, 2014, 61(1): 162-172. |
| [25] |
Jin W, Censor Y, Jiang M. Bounded perturbation resilience of projected scaled gradient methods[J]. Computational Optimization and Applications, 2015, 63(2): 365-392. |
| [26] |
Herman G T, Lent A, Lutz P H. Relaxation methods for image reconstruction[J]. Communications of the ACM, 1978, 21(2): 152-158. |
| [27] |
Kaczmarz S. Angenaherte aufl osung von systemen linearer gleichungen[J]. Bulletin International de L' Academie Polonaise des Sciences et des Lettres, 1937, 35: 355-357. |
| [28] |
Shepp L A, Vardi Y. Maximum likelihood reconstruction for emission tomography[J]. IEEE Transactions on Medical Imaging, 1982, 1(2): 113-122. |
| [29] |
Lange K, Carson R. EM reconstruction algorithms for emission and transmission tomography[J]. Journal of Computer Assisted Tomography, 1984, 8(2): 306-316. |
| [30] |
张艳春. Superiorization算法的理论研究和改进及其在CT和MRI中的应用[D].开封: 河南大学, 2016. Zhang Y C. Theoretical study and improvement of superiorization algorithm and its application in CT and MRI[D]. Kaifeng: Henan University, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10475-1016202337.htm |
| [31] |
Cai W W, Li X S, Li F, et al. Numerical and experimental validation of a three-dimensional combustion diagnostic based on tomographic chemiluminescence[J]. Optics Express, 2013, 21(6): 7050-7064. |
| [32] |
Twynstra M G, Daun K J. Laser-absorption tomography beam arrangement optimization using resolution matrices[J]. Applied Optics, 2012, 51(29): 7059-7068. |
| [33] |
Terzija N, Davidson J L, Garcia-Stewart C A, et al. Image optimization for chemical species tomography with an irregular and sparse beam array[J]. Measurement Science and Technology, 2008, 19(9): 094007. |



