在高Mach数飞行条件下, 飞行器表面气体会出现振动能激发、离解及电离等现象, 对气动力/热分布产生显著影响[1]; 开展该类现象的模拟对地面试验设备的能力提出了极高的要求[2]. 自由活塞激波风洞是一类得到广泛应用的高焓地面模拟设备; 从20世纪中叶以来, 自由活塞激波风洞在高温气体动力学研究领域发挥着关键作用[3-4], 典型如澳大利亚昆士兰大学的T4[5-6], 美国加州理工学院的T5[7-8], 德国DLR的HEG[9-10], 日本国家航天实验中心的HIEST[11-12], 英国牛津大学的T6[13]等. 中国航天空气动力技术研究院自主研发了一套2 m量级的自由活塞激波风洞, 并在2017年投入使用[14].
自由活塞激波风洞的结构可分为4个主要部分: 活塞压缩器、激波管、喷管和试验段(及其附属的真空罐体). 此类设备运行原理与激波风洞相似, 即通过膜片的破裂产生入射激波, 入射激波在激波管末端(激波管与喷管连接处)反射后对管内试验气体形成二次加压加热, 随后高温高压试验气体经过喷管并形成高Mach数试验流场. 自由活塞激波风洞的特点在于利用重活塞压缩高压段内的气体(一般为氦气、氩气或二者的混合气体), 使其达到较高的温度与压力, 大幅提升破膜后激波管内激波强度, 进而提升驻室气体的总温, 满足高总焓值模拟需求[15-16]. 活塞压缩器的运行状态很大程度上决定了自由活塞激波风洞的性能, 而压缩管内流动状态的计算是活塞压缩器运行预测的关键和主要的难点所在. 因此, 从该类设备诞生以来, 压缩管内的流动规律受到持续的关注.
对活塞压缩器压缩管中的流动预测包括理论和数值两类方法. Stalker在提出自由活塞激波风洞概念之初便对压缩管的运行进行了理论建模[17], 随后压缩管的模型被Hornung[18], Itoh等[19],Tanno等[20]和朱浩等[21-22]进行了发展和完善, 提出了诸如压缩管调谐运行、延长定压驱动时间等一系列运行理念. 压缩管运行理论研究主要基于压缩管内气体等熵压缩的假设. 压缩管流动的数值预测方法包括Euler法[23-24]、Lagrange法[25-26]及任意Lagrange Euler方法(arbitrary Lagrange Euler, ALE)[27-28]等. 数值模拟工作通常以破膜后激波管的流动为主要研究对象, 对压缩管内流动的深入分析相对较少. 在真实压缩管流动中, 存在激波和对流传热等非等熵现象, 这些现象在数值模拟和实验结果中亦有所体现[20, 29]; 非等熵现象的存在会导致理论模型对活塞压缩器运行的预测出现误差, 影响其准确度. 虽然一些基于经验的方法被用于修正这些现象所产生的影响[19], 但目前非等熵效应对压缩管流动的影响研究仍然较为欠缺, 激波、传热等现象引起的熵变及其导致的等熵理论与真实压缩过程间的预测误差值得评估.
针对上述背景, 本文对FD-21自由活塞激波风洞活塞压缩器进行准一维数值模拟和理论分析. 通过数值结果与风洞实验结果的对比, 对典型流动进行阐述和解释, 深化对压缩管流动中复杂波系现象及参数变化过程的认识; 在此基础上, 研究压缩过程中压缩管内气体熵的变化规律, 并初步探索归一化的方法; 进一步地, 利用熵变曲线对现有理论进行修正, 估算熵变对被压缩气体温度和压力的影响, 以期为活塞压缩器的运行提供更为可靠的理论指导.
1 研究方法 1.1 实验设备及运行状态FD-21风洞是一座采用自由活塞压缩惰性气体破膜形成强激波, 从而提升试验气体总温的大尺寸高焓激波风洞. 该风洞主要结构由图 1(a)给出. 其中, 高压储气室容积24 m3, 可承压20 MPa; 压缩管长75 m, 内径668 mm; 激波管长34 m, 内径290 mm; Ma=10喷管出口直径1.8 m; 试验段及真空罐总容积230 m3. 投入使用的活塞质量为124~400 kg. 压缩管与激波管通过一道08Al材质的主膜片隔开, 膜片上铣“*”形槽以保证其破裂的稳定性. 该风洞于2017年完成硬件设备建设与活塞压缩器的初步调试[14, 30].

|
| 图 1 FD-21自由活塞激波风洞 Fig.1 FD-21 free piston shock tunnel |
为监测压缩管内的流动状态并确定主膜片的破膜压力, 压缩管内设置了一系列应变压力传感器. 图 1(b)是风洞压缩管与激波管结构及压力测点位置的示意图. 本文重点研究喷管名义总温为2 700 K的试验状态, 其主要运行参数由表 1给出. 表中pA0,pCT0分别为高压储气室和压缩管的初始压力, mp为活塞质量, mHe, CT和mAr, CT分别为压缩管内初始充入氦气和氩气的质量.
| 下载CSV 表 1 活塞压缩器运行参数 Tab.1 Experimental condition of the piston compressor |
朱浩归纳了自由活塞激波风洞中活塞压缩过程的理论模型[21, 31]. 高压储气室气体经过等熵非定常膨胀至活塞速度后作用在活塞背面, 驱动活塞向前移动; 压缩管内氦氩气体被活塞压缩, 这一压缩过程也被假设为等熵的. 主膜片破膜后, 压缩管内高压氦氩气体进入激波管, 激波管入口处流动Mach数为1. 活塞压缩过程的控制方程为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{{\rm{d}}^2}{x_{\rm{p}}}}}{{{\rm{d}}{t^2}}} = \frac{1}{{{m_p}}}\frac{{{\rm{ \pi }}{d_{{\rm{CT}}}}^2}}{4}\left( {{p_{{\rm{dr}}}} - {p_{{\rm{CT}}}}} \right) + f}\\ {{p_{{\rm{dr}}}} = {p_{{\rm{A0}}}}{{\left( {1 - \frac{{{\gamma _{\rm{A}}} - 1}}{2}\frac{1}{{{c_{{\rm{A0}}}}}}\frac{{{\rm{d}}{x_{\rm{p}}}}}{{{\rm{d}}t}}} \right)}^{\frac{{2{\gamma _A}}}{{{\gamma _A}^{ - 1}}}}}}\\ {{\rm{d}}{p_{{\rm{CT}}}} = \frac{{{\gamma _{{\rm{CT}}}}{p_{{\rm{CT}}}}}}{{ - x}}{u_{{\rm{p}},{\rm{n}}}}{\rm{d}}t}\\ {{u_{{\rm{p}},{\rm{n}}}} = \frac{{{\rm{d}}{x_{\rm{p}}}}}{{{\rm{d}}t}},{\rm{before}}\;\;{\rm{diaphragm}}\;\;{\rm{rupture}}}\\ {{u_{{\rm{p}},{\rm{n}}}} = \frac{{{\rm{d}}{x_{\rm{p}}}}}{{{\rm{d}}t}} - \frac{{{d_{{\rm{ST}}}}^2}}{{{d_{{\rm{CT}}}}^2}}\frac{1}{{{\rho _{{\rm{CT}}}}}}\left( {{{\left( {{\gamma _{{\rm{CT}}}}\frac{{{p_{{\rm{CT}}}}}}{{{\rho _{{\rm{CT}}}}}}} \right)}^{\frac{1}{2}}}{{\left( {\frac{2}{{{\gamma _{{\rm{CT}}}} + 1}}} \right)}^{\frac{1}{2}}}} \right) \cdot }\\ {\;\;\;\;\;\;\;\;\left( {{\rho _{{\rm{CT}}}}{{\left( {\frac{2}{{{\gamma _{{\rm{CT}}}} + 1}}} \right)}^{\frac{1}{{{\gamma _{{\rm{CT}}}} - 1}}}}} \right),{\rm{after}}\;\;{\rm{diapragm}}\;\;{\rm{rupture}}}\\ {\frac{{{\rm{d}}{\rho _{{\rm{CT}}}}}}{{{\rm{d}}t}} = \frac{{{\rho _{{\rm{CT}}}}}}{{ - {x_{\rm{p}}}}}{u_{{\rm{p}},{\rm{n}}}},{\rm{after}}\;\;{\rm{diapragm}}\;\;{\rm{rupture}}} \end{array}} \right. $ | (1) |
式中,t为时间, dCT和dST分别为压缩管和激波管直径, xp为活塞的位置, pdr和pCT分别为高压储气室气体在活塞表面形成的压力和被压缩氦氩气体的压力, γA, γCT分别为高压储气室内气体和被压缩气体比热比, cA0为高压储气室气体初始声速, up, n表示考虑气体流出后被压缩气体的等效压缩速度, f为活塞摩擦力项. 求解采用4阶Runge-Kutta方法. 该理论模型是FD-21自由活塞激波风洞设计与状态调试的重要依据[21-22, 26, 31-34].
1.3 准一维数值模拟程序在利用理论模型对压缩管流动进行预测的同时, 本文也开展了准一维数值模拟工作, 以获得压缩管内更多流动细节. 数值模拟程序基于Lagrange坐标系, 程序中网格运动、动量及能量方程分别为
| $ \left\{ \begin{array}{l} {\rm{d}}{x_{j \pm 1/2}}/{\rm{d}}t = {u_{j \pm 1/2}}\\ {\rm{d}}\left( {{m_j}{{\bar u}_j}} \right)/dt = {p_{j - 1/2}}{A_{j - 1/2}} - {p_{j + 1/2}}{A_{j + 1/2}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\bar p}_j}\left( {{A_{j + 1/2}} - {A_{j - 1/2}}} \right) - {{\bar F}_{{\rm{wall}}}}\\ {\rm{d}}\left( {{m_j}{{\bar e}_j} + {m_j}\bar u_j^2/2} \right)/{\rm{d}}t = {p_{j - 1/2}}{A_{j - 1/2}}{u_{j - 1/2}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{j + 1/2}}{A_{j + 1/2}}{u_{j + 1/2}} + {{\bar q}_j} \end{array} \right. $ |
式中, xj±1/2和uj±1/2分别为网格界面的位置及其移动速度, mj为网格内气体质量, uj为网格内气体平均速度, pj±1/2和Aj±1/2分别为网格界面处的压力和管路面积, ej和uj分别为网格气体平均比内能和平均速度, Fwall和qj分别为网格内壁面摩擦力和热流率[25]. 计算采用NND格式, 时间推进为2阶Runge-Kutta方法, 网格的移动速度uj±1/2通过求解Riemann问题获得, Riemann求解器为HLLC与精确Riemann解混合求解器(当界面两侧物理量变化不大时用HLLC求解, 当变化较大时求精确Riemann解). 活塞在高压储气室一侧的压力通过理论模型进行计算(即式(1)中的pdr), 在压缩管一侧的压力由数值模拟直接给出. 初始条件下, 压缩管内为氦氩混合气体, 每个网格内的壁面摩阻Fwall和网格与壁面的传热qj分别通过文献[35]给出的流动阻力公式和文献[36]给出湍流边界层传热公式进行计算.
| $ \left\{ \begin{array}{l} {{\bar F}_{{\rm{wall}}}} = - {\rm{ \mathsf{ π} }}{{\bar \rho }_j}f{{\bar u}_j}\left| {{{\bar u}_j}} \right|\bar D\left( {{x_{j + 1/2}} - {x_{j - 1/2}}} \right)/8\\ {{\bar q}_j} = h{\rm{ \mathsf{ π} }}\bar D\left( {{x_{j + 1/2}} - {x_{j - 1/2}}} \right)\left( {{T_{\rm{w}}} - {{\bar T}_{{\rm{aw}}}}} \right) \end{array} \right. $ |
式中, ρj为网格内气体平均密度, f为基于Reynolds数和可压缩性修正的摩擦因子, D为水力学直径, h为热传导系数, Tw和Taw分别为壁面温度和绝热壁温. 计算采用迭代式自适应时间步以在CFL数小于0.5的前提下提高计算速度. 数值计算的初始条件与表 1给出的实验条件一致, 压缩管内气体网格数为1 000.
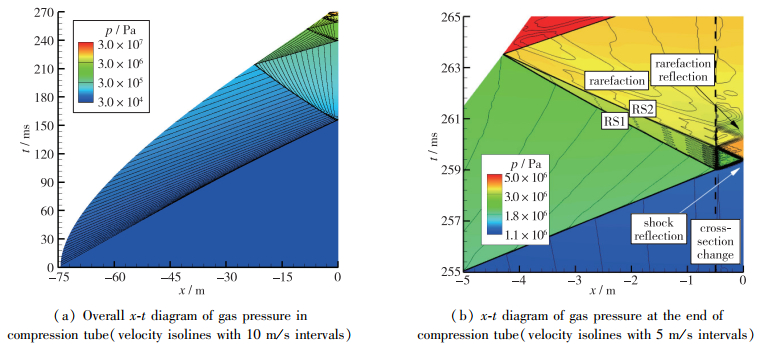
2 结果与讨论 2.1 压缩管中的流动现象图 2(a)给出数值模拟中压缩管x-t压力云图. 从图中可知, 在高压空气的驱动下, 活塞逐渐加速到一个相对稳定的速度. 活塞的加速运动在压缩管中产生了一系列压缩波并汇聚为弱激波; 在其传播过程中由于后方压缩波的追赶而不断增强. 此后这一激波在活塞与压缩管末端膜片之间多次反射, 持续对压缩管内的氦氩气体形成压缩. 图 2(b)给出了通过压缩管末端流动的x-t压力云图, 从图中可知, 由于压缩管末端膜片前存在管路直径的变化, 激波在压缩管末端形成多次反射. 入射激波部分在变截面处反射, 形成第1反射激波(reflected shock 1, RS1); 部分传入细直径管路并在膜片位置反射. 反射激波从右向左到达变截面位置后形成透射(图中标为第2反射激波reflected shock 2, RS2)并在该位置反射稀疏波. 稀疏波向右侧传播并在膜片位置反射. 在压缩的初期, 后续的波系会追赶上第1反射激波, 因此压缩管中的流动整体比较规则; 在压缩的后期, 由于活塞与膜片距离较近, 后续波系在追赶上第1反射激波前就已在活塞端面反射, 流场中的多个波系会一直持续.
|
| 图 2 压缩管内流动x-t图 Fig.2 x-t diagrams of the compression tube flow |
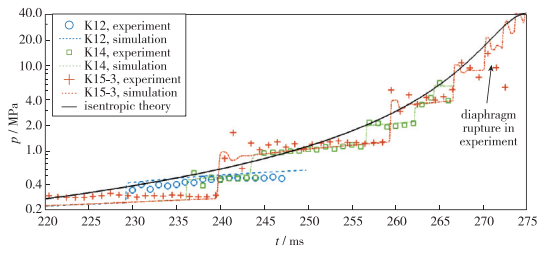
图 3给出了压缩管不同位置测压实验结果与计算及理论结果的对比. 从该图可知, 数值模拟对于激波每次经过后的压力均有较好的刻画. 等熵压缩理论可大致反映压缩管内压力变化的趋势, 但在压缩的后期(260 ms以后), 等熵压缩理论压力预测结果与激波刚反射时的波后压力相当, 高于压缩管内压力的总体水平. 实验中的膜片破裂发生于271 ms, 此后压力测量值开始降低; 理论和数值结果均只考虑氦氩气体被压缩过程, 未在计算中模拟破膜现象. 此外, 由于压缩管末端变直径形成的多次反射激波-稀疏波系结构, 测点位置的压力值在压缩末期会有剧烈振荡, 这在压力测量结果及数值结果中均有体现.
|
| 图 3 压缩管压力的理论、数值与实验结果对比 Fig.3 Comparison of theoretical, numerical and experimental results of gas pressure in compression tube |
由上述实验和数值结果可知, 由于活塞的起动加速, 压缩管内会产生激波, 并伴随压缩过程在压缩管内多次反射. 激波的传播会导致压缩管内熵的增加. 气体的黏性导致的熵变包括黏性耗散引起的熵增和边界层对流传热所导致的熵减, 其中后者占据主要地位[37]. 为探索活塞压缩器运行状态对系统熵变的影响规律, 本文设计了一系列计算状态开展数值模拟. 具体工况由表 2给出, 主要考察的参数包括高压储气室空气压力pA0, 活塞质量mp, 压缩管总长LCT, 被压缩气体初始压力pCT0. 数值结果中压缩管内的熵变水平以平均比熵变化量s-s0表示, 其表达式为
| $ s - {s_0} = \sum\limits_j {\left( {{m_j}\frac{{{R_{{\rm{CT}}}}}}{{{\gamma _{{\rm{CT}}}} - 1}}\ln \left( {\frac{{{{\bar p}_j}}}{{{p_{{\rm{CT0}}}}}}} \right){{\left( {\frac{{{{\bar p}_j}}}{{{\rho _{{\rm{CT0}}}}}}} \right)}^{ - \gamma }}} \right)/\sum\limits_j {{m_j}} } $ |
| 下载CSV 表 2 压缩管熵变的计算工况 Tab.2 Simulation conditions of entropy change examination in compression tube |
被压缩气体的压缩程度通过压缩比λ表示, 其表达式为
| $ \lambda = {V_0}/V $ |
式中,RCT为被压缩气体的气体常数, ρj为网格内气体平均密度, ρCT0为被压缩气体的初始密度, V0和V分别是被压缩气体初始体积和被压缩后的体积. 每个计算状态均包含无黏无传热和有黏有传热两个算例: 激波导致的熵变直接由无黏无传热结果提取得到; 黏性引起的熵变通过有黏有传热工况提取的熵变与无黏无传热结果相减给出.
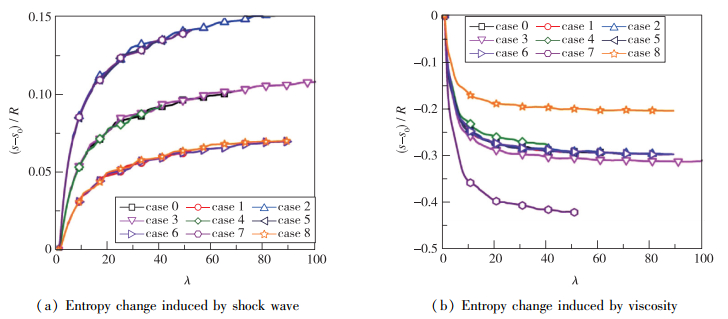
图 4(a), (b)分别给出了不同计算条件下激波所引起的熵变和黏性引起的熵变. 对流传热(黏性)引起的熵减也明显强于激波引起的熵增, 在被压缩气体熵的变化中占据主导地位. 除了熵变与压缩比的显著相关性之外, 激波引起的熵增主要与驱动压力、活塞质量和压缩管总长相关, 受被压缩气体初压的影响不显著, 该类熵变与组合参数LCTpA0/mp成正比; 黏性引起的熵减主要与压缩管总长相关, 受其他参数的影响不显著, 该类熵变可认为与参数LCT成正比. 将两类熵变分别归一化, 其表达式为
| $ \left\{ \begin{array}{l} {\left( {\frac{{s - {s_0}}}{{{R_{{\rm{CT}}}}}}} \right)_{{\rm{all}}}} = {\left( {\frac{{s - {s_0}}}{{{R_{{\rm{CT}}}}}}} \right)_{{\rm{shock}}}} + {\left( {\frac{{s - {s_0}}}{{{R_{{\rm{CT}}}}}}} \right)_{{\rm{heat}}\;\;{\rm{transfer}}}}\\ {\left( {\frac{{s - {s_0}}}{{{R_{{\rm{CT}}}}}}} \right)_{{\rm{shock}}}} = \frac{{{L_{{\rm{CT}}}}}}{{75}}\frac{{{p_{{\rm{A0}}}}}}{{2.86 \times {{10}^6}}}\frac{{205}}{{{m_{\rm{p}}}}} \cdot \frac{{{s_{\rm{I}}}\left( \lambda \right)}}{{{R_{{\rm{CT}}}}}}\\ {\left( {\frac{{s - {s_0}}}{{{R_{{\rm{CT}}}}}}} \right)_{{\rm{viscosity}}}} = \frac{{{L_{{\rm{CT}}}}}}{{75}} \cdot \frac{{{s_{\rm{V}}}\left( \lambda \right)}}{{{R_{{\rm{CT}}}}}} \end{array} \right. $ | (2) |
|
| 图 4 压缩管内熵变曲线 Fig.4 Entropy change profile in compression tube |
式中,sI和sV分别为归一化后的激波和黏性分别引起的熵变. 二者与压缩比的关系可由拟合公式式(3)近似给出.
| $ \left\{ \begin{array}{l} \frac{{{s_{\rm{I}}}}}{{{R_{{\rm{CT}}}}}} = 0.023538\ln \lambda \\ \frac{{{s_{\rm{V}}}}}{{{R_{{\rm{CT}}}}}} = - 0.3 + \exp \left( {\ln 0.3 - 0.1788\left( {\lambda - 1} \right)} \right) \end{array} \right. $ | (3) |
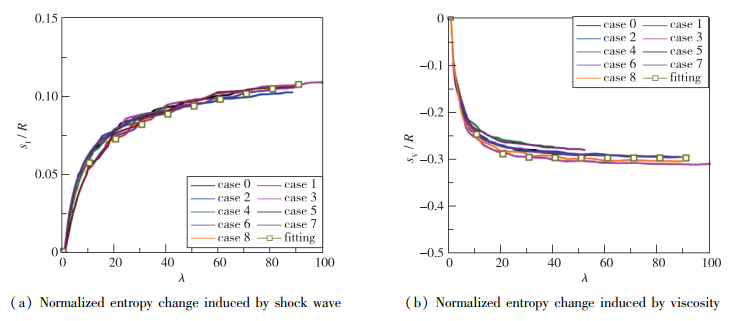
图 5给出了不同条件计算结果的归一化情况及其与拟合公式的对比. 拟合公式可以较精确地反映两类熵变随压缩比的变化规律, 利用式(2)和式(3)即可对压缩过程中压缩管内的熵变进行预测.
|
| 图 5 归一化的压缩管熵变曲线 Fig.5 Normalized entropy change profile in compression tube |
压缩管内气体受到压缩之后温度升高, 与壁面进行热交换后总熵降低, 其幅度大于黏性耗散和激波引起的熵增, 主导了压缩管内熵的变化. 通过熵的定义可知, 同样压缩比条件下, 较低的熵值对应较低的压力. 然而, 由于压缩管内激波的存在导致压力分布不均, 增大了压缩管压力的等熵理论结果和数值结果之间的对比难度, 在图 3所给出的压力对比中, 可以看到等熵理论结果比数值结果略高的趋势, 但这一对比缺乏直观性和定量性. 通过对图 2的观察可知, 在激波与活塞端壁接触并发生反射的瞬间, 压缩管内压力较为平均, 方便理论结果与数值结果的对比.
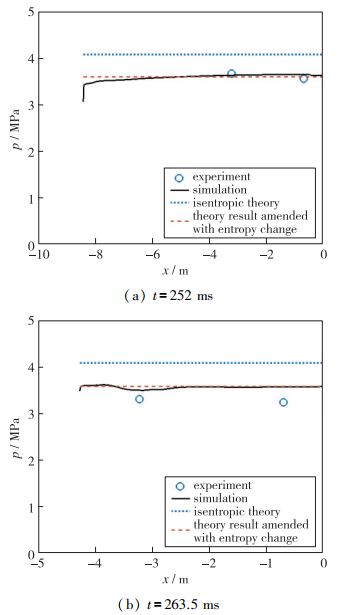
图 6给出了t=252 ms和t=263.5 ms两个不同时刻压缩管内压力分布的等熵理论预测值、数值模拟结果和实验测量结果. 从图中的对比可知, 考虑非等熵效应的数值结果对压缩管内的压力预测更为准确, 等熵压缩理论的压力预测偏高约10%. 利用式(2)和式(3)所给出的压缩管内熵变曲线, 通过式(4)
| $ \left\{ \begin{array}{l} {p_{{\rm{CT}}}} = {p_{{\rm{CT0}}}}{\lambda ^{{\gamma _{{\rm{CT}}}}}}\exp \left( {\left( {{\gamma _{{\rm{CT}}}} - 1} \right)\left( {s - {s_0}} \right)/{R_{{\rm{CT}}}}} \right)\\ {T_{{\rm{CT}}}} = {T_{{\rm{CT0}}}}{\lambda ^{{\gamma _{{\rm{CT - 1}}}}}}\exp \left( {\left( {{\gamma _{{\rm{CT}}}} - 1} \right)\left( {s - {s_0}} \right)/{R_{{\rm{CT}}}}} \right) \end{array} \right. $ | (4) |
可以对压缩管内气体温度和压力的总体水平进行估算, 式中TCT和TCT0分别为压缩管内平均温度及其初始值. 在对应压缩比条件下, 熵变修正后的压力预测结果在图 6中通过红色虚线给出. 与原有理论相比, 这一结果与数值解和实验值均更为吻合. 这一压力值比等熵结果偏低10%左右, 而通过式(4)的形式可知, 非等熵条件下压缩管内的温度也会比等熵结果低约10%. 这一降幅也与文献[19]中给出的传热导致被压缩气体温降程度一致. 这两方面的差异均会导致实际破膜产生的激波Mach数低于理论预测值. 换言之, 原有基于等熵压缩的活塞压缩器运行理论因其忽略了压缩管内的熵变而高估了设备在同等压缩比下的驱动能力.
|
| 图 6 典型时刻压缩管内压力分布的等熵压缩理论、数值模拟和实验结果对比 Fig.6 Comparison of theoretical, numerical and experimental results of pressure distribution in compression tube at typical moments |
本文针对FD-21自由活塞激波风洞活塞压缩器的典型运行状态展开数值模拟和理论研究, 分析了压缩管内的波系结构和参数变化, 归纳了压缩过程的熵变规律, 并进一步提出了活塞压缩器理论模型的非等熵修正方法. 主要结论包括:
(1) 活塞的加速过程会在压缩管中生成激波, 并在含有变直径结构的压缩管末端形成复杂的反射现象, 导致压缩管末端的压力振荡;
(2) 等熵理论对压缩管内压力的预测值较数值和实验结果偏高, 典型时刻理论预测压力较数值结果高约10%, 表明压缩管内熵的变化对压力等参数产生了较为明显的影响;
(3) 压缩管内的熵变来源可分为两项: 激波引起的熵变和黏性引起的熵变. 利用一系列变参数的数值模拟, 两项熵变可分别被归一化, 归一化后的熵变仅与压缩比相关;
(4) 通过对归一化结果进行拟合, 利用归一化分析的结果可以获得了压缩过程中压缩管内的熵变公式, 并对理论预测模型进行了修正, 修正后压缩管内压力预测值与实验和数值结果更为吻合.
致谢 感谢国家重点研发计划资助项目(2019YFA0405200和2019YFA0405300)、装发预研基金(61402060502)和自然科学基金(11972332)的支持.| [1] |
Anderson J D Jr. Hypersonic and high-temperature gas dynamics[M]. 2nd ed.. Reston: American Institute of Aeronautics and Astronautics, 2006.
|
| [2] |
Lu F K, Marren D. Advanced hypersonic test facilities[M]. Reston: American Institute of Aeronautics and Astronautics, Inc, 2002.
|
| [3] |
陈星, 谌君谋, 毕志献, 等. 自由活塞高焓脉冲风洞发展历程及试验能力综述[J]. 实验流体力学, 2019, 33(4): 65-80. Chen X, Shen J M, Bi Z X, et al. Review on the development of the free-piston high enthalpy impulse wind tunnel and its testing capacities[J]. Journal of Experiments in Fluids Mechanics, 2019, 33(4): 65-80. (in Chinese) |
| [4] |
Igra O, Seiler F. Experimental methods of shock wave research[M]. Switzerland: Springer, 2016.
|
| [5] |
Gai S L. Free piston shock tunnels: developments and capabilities[J]. Progress in Aerospace Sciences, 1992, 29: 1-41. DOI:10.1016/0376-0421(92)90002-Y |
| [6] |
Boyce R R, Takahashi M, Stalker R J. Mass spectrometric measurements of driver gas arrival in the T4 free-piston shock-tunnel[J]. Shock Waves, 2005, 14(5/6): 371-378. DOI:10.1007/s00193-005-0276-3 |
| [7] |
Hornung H. Performance data of the new free-piston shock tunnel at GALCIT[R]. AIAA 1992-3943, 1992.
|
| [8] |
Marineau E C, Hornung H G. Heat flux calibration of T5 hypervelocity shock tunnel conical nozzle in air[R]. AIAA 2009-1158, 2009.
|
| [9] |
Beck W H, Eitelberg G, McIntyre T J, et al. The high enthalpy shock tunnel in Göttingen[C]. Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville: American Institute of Aeronautics and Astronau-tics, 1992.
|
| [10] |
Eitelberg G. Calibration of the HEG and its use for verification of real gas effects in high entalpy flows[R]. AIAA 93-5170, 1993.
|
| [11] |
ItohK, Komuro T, Sato K, et al. Characteristics of free-piston shocktunnel HIEST: 1st report, tuned operation of free-piston driver[J]. Transactions of the Japan Society of Mechanical Engineers Series B, 2002, 68: 2968-2975. DOI:10.1299/kikaib.68.2968 |
| [12] |
Itoh K, Ueda S, Komuro T, et al. Hypervelocity aerothermodynamic and propulsion research using a high enthalpy shock tunnel HIEST[R]. AIAA 99-4960, 1999.
|
| [13] |
McGilvray M, Doherty L J, Morgan R G, et al. T6: the Oxford University stalker tunnel[R]. AIAA 2015-3456, 2015.
|
| [14] |
Chen X, Bi Z X, Ma H D, et al. Development of a new large-scale free-piston shock tunnel[C]. Proceedings of the 21st International Space Plane and Hypersonic Systems and Technology Conference. Xiamen: American Institute of Aeronautics and Astronautics, 2017.
|
| [15] |
谌君谋, 陈星, 毕志献, 等. 高焓激波风洞试验技术综述[J]. 空气动力学学报, 2018, 36(4): 543-554. Shen J M, Chen X, Bi Z X, et al. Review on experimental technology of high enthalpy shock tunnel[J]. Acta Aerodynamica Sinica, 2018, 36(4): 543-554. DOI:10.7638/kqdlxxb-2017.0165 (in Chinese) |
| [16] |
卢洪波, 陈星, 谌君谋, 等. 新建高焓激波风洞Ma=8飞行模拟条件的实现与超燃实验[J]. 气体物理, 2019, 4(5): 13-24. Lu H B, Chen X, Shen J M, et al. Flight condition achievement of Mach number 8 in a new shock tunnel of CAAA and its scramjet experimental investigation[J]. Physics of Gases, 2019, 4(5): 13-24. (in Chinese) |
| [17] |
Stalker R J. A study of the free-piston shock tunnel[J]. AIAA Journal, 1967, 12(5): 2160-2165. |
| [18] |
Hornung H G. The piston motion in a free-piston driver for shock tubes and tunnels[R]. GALCIT FM 88-1, 1988.
|
| [19] |
Itoh K, Ueda S, Komuro T, et al. Improvement of a free piston driver for a high-enthalpy shock tunnel[J]. Shock Waves, 1998, 8(4): 215-233. DOI:10.1007/s001930050115 |
| [20] |
Tanno H, Itoh K, Komuro T, et al. Experimental study on the tuned operation of a free piston driver[J]. Shock Waves, 2000, 10: 1-7. DOI:10.1007/s001930050174 |
| [21] |
朱浩. 自由活塞激波风洞理论设计与运行模拟[R]. 北京: 中国航天空气动力技术研究院, 2012: 35-67. Zhu H. Theoretical design and operating simulation of the free piston shock tunnel[R]. Beijing: China Academy of Aerospace Aerodynamics, 2012: 35-67(in Chinese). |
| [22] |
朱浩, 沈清, 宫建. 自由活塞激波风洞定压驱动时间研究[J]. 空气动力学学报, 2014, 32(1): 45-50. Zhu H, Shen Q, Gong J. The constant pressure time of piston driver in free piston shock tunnel[J]. Acta Aerodynamica Sinica, 2014, 32(1): 45-50. (in Chinese) |
| [23] |
Mitsuda M, Oda T, Kurosaka T, et al. Numerical and experimental study for free piston expansion tube[R]. AIAA 94-2528, 1994.
|
| [24] |
Wilson G J. Time-dependent quasi-one-dimensional simulations of high enthalpy pulse facilities[C]. Proceedings of the AIAA 4th International Aerospace Planes Conference, Orlando: American Institute of Aeronautics and Astronautics, 1992.
|
| [25] |
Jacobs P A. Quasi-one-dimensional modeling of a free-piston shock tunnel[J]. AIAA Journal, 1994, 32(1): 137-145. DOI:10.2514/3.11961 |
| [26] |
朱浩, 江海南, 张冰冰. 自由活塞激波风洞的入射激波衰减[J]. 航空学报, 2017, 38(12): 121328. Zhu H, Jiang H N, Zhang B B. Attenuation of incident shock waves in free piston shock tunnels[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(12): 121328. (in Chinese) |
| [27] |
Bensassi K, Lani A, Chazot O, et al. Arbitrary Lagrangian Eulerian simulation of a moving piston in hypersonic ground test facility[R]. AIAA 2012-3265, 2012.
|
| [28] |
李海燕, 李志辉, 吕治国, 等. 自由活塞压缩管ALE方法数值模拟[J]. 力学学报, 2016, 48(2): 348-352. Li H Y, Li Z H, Lv Z G, et al. Arbitrary Lagrangian Eulerian simulation of free piston compression tube[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(2): 348-352. (in Chinese) |
| [29] |
Schemperg K, Mundt C. Study of numerical simulations for optimized operation of the free piston shock tunnel HELM[R]. AIAA 2008-2653, 2008.
|
| [30] |
Gu S D, Olivier H. Capabilities and limitations of existing hypersonic facilities[J]. Progress in Aerospace Sciences, 2020, 113: 100607. DOI:10.1016/j.paerosci.2020.100607 |
| [31] |
朱浩. 自由活塞激波风洞理论[M]. 北京: 科学出版社, 2019. Zhu H. The theories of free piston shock tunnels[M]. Beijing: Science Press, 2019. (in Chinese) |
| [32] |
张冰冰, 毕志献, 朱浩, 等. FD-21高能脉冲风洞重活塞压缩过程的计算及试验研究[C]. 第十八届全国激波与激波管学术会议论文集, 北京: 中国力学学会激波与激波管专业委员会, 2018. Zhang B B, Bi Z X, Zhu H, et al. Experimental study of the compression process in a free piston shock tunnel FD21[C]. Proceedings of the 18th Chinese National Symposium on Shock Waves, Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2018(in Chinese). |
| [33] |
易翔宇, 陈星, 毕志献, 等. 自由活塞激波风洞压缩管-激波管流动分析及4000K状态调试[C]. 首届中国空气动力学大会, 绵阳: 中国空气动力研究与发展中心, 2018. Yi X Y, Chen X, Bi Z X, et al. Analysis of the compression-shock tube flow in a free piston shock tunnel and the tuning of 4000 K test condition[C]. Proceedings of the 1st Chinese Conference of Aerodynamics, Mianyang: Chinese Aerodynamics Research Society, 2018(in Chinese). |
| [34] |
Zhu H, Shen Q, Gong J. Fast simulation of flows in shock tube with area change[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30(3): 260-263. |
| [35] |
Schlichting H. Boundary-layer theory[M]. Kestin J, trans. New York: McGraw-Hill, 1968.
|
| [36] |
Holman J P. Heat transfer[M]. New York: McGraw-Hill, 1981.
|
| [37] |
童秉纲, 孔祥言, 邓国华. 气体动力学[M]. 北京: 高等教育出版社, 2012. Tong B G, Kong X Y, Deng G H. Gas dynamics[M]. Beijing: Higher Education Press, 2012. (in Chinese) |




