| 基于小波变换的SAR图像处理研究 |
2. 海军大连舰艇学院 舰船指挥系, 大连 116000;
3. 海军大连舰艇学院 学员五大队, 大连 116000
2. Ship Command Department, Dalian Naval Academy of Navy, Dalian 116000, China;
3. Five Cadets Team, Dalian Naval Academy of Navy, Dalian 116000, China
SAR图像能够体现目标的结构与电磁散射的特征, 其图像对目标位置、方位角等因素极其敏感, 而目标区域混杂的大量杂波极大干扰了目标位置、方位角的检测, 进而影响了目标的识别、鉴定能力。在SAR图像目标识别之前首先对二维信号进行小波变换处理, 之后将二维信号从时域转换到变换域中, 再对变换域中的二维信号变换系数进行处理, 最后对处理后的系数进行反变换, 最终实现将图像去除噪声的目的。
1 SAR目标识别基本流程SAR目标识别的基本原理是利用目标与环境在图像灰度、纹理及几何构成等方面的差异, 检测出和目标对应的单元进而分类识别, 其基本识别流程由图像去噪、分割、特征提取、分类识别及识别结果输出等步骤组成[1], 如图 1所示。
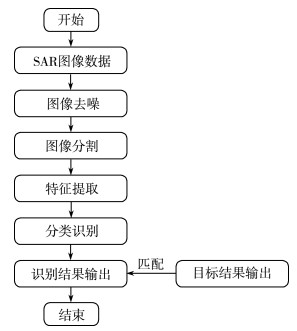 |
| 图 1 SAR目标识别流程图 |
由于SAR成像受干扰斑噪声的影响会产生拥有均匀散射系数但不具有均匀灰度的二维信号, 导致出现较多斑点, 严重影响SAR实际运用, 因此选择相关噪声抑制的方法应当兼顾消除噪声与图像细节损耗两个方面。
图像分割指为了减少背景杂波对目标识别的影响, 将图像根据其特性分割成若干区域并提取其中主要目标的方法。接着通过特征提取步骤, 对分割出的主要目标在排除斑点噪声和虚警的基础之上, 提取其纹理、对比度、傅里叶系数等数学特征及几何特征SAR图像。最后以提取的特征为依据经过分类识别步骤判断目标属性, 选择相应算法与数据库中的特征进行匹配, 进而实现对目标的识别。
2 小波变换在SAR图像消噪中的应用分析通常情况下SAR图像生成与传输过程中会受到各种各样噪声的干扰, 而二维信号混杂噪声的原因在于其搜集、获取、编码及传输过程中均不同程度上被可视或不可视的噪声“污染”, 因此给信号的处理、传输及存储造成极大的影响[2]。一旦信噪比(SNR)低于一定数值, 会严重影响图像质量并使图像的熵增大进而掩盖图像中的重要细节, 由此妨碍到信号数据压缩的效果。
对二维信号消噪由最开始在空域内进行发展为在变换域中进行, 对二维信号变换域消噪的本质是采用某种去噪方法进行变换, 将信号从时域转换到变换域中, 接着对变换域中的信号按照此种消噪方法处理, 最后对处理后的信号进行反变换从而实现对二维信号消噪的目的, 对二维信号进行消噪的方法主要有小波变换法、均值滤波消噪法及中值滤波消噪法等。基于小波变换具有低熵性、多分辨率特性、去相关性、基函数选择灵活等优势, 可以考虑在SAR图像去噪环节采用小波变换的方式实现消噪。
2.1 小波变换二维消噪原理二维信号小波变换目前研究中主要以可分离小波为主, 下面给出了构造二维可分离正交小波基的方法[2]。二维多分辨率分析与一维类似, 但空间L2(R)变成L2(R*R), 一维中引入的尺度函数φ(x)变为φ(x, y)。
设{Vj}j∈Z是L2(R)的一个多分辨率分析, 则可以证明, 张量空间{Vj2}j∈Z: Vj2=Vj⊕Vj构成L2(R*R)的一个多分辨率分析, 并且二维多分辨率分析{Vj2}j∈Z的二维尺度函数φ(x, y)为:
| $ \varphi(x, y)=\varphi(x) \varphi(y) \text { 。} $ | (1) |
其中,φ(x)是{Vj}j∈Z尺度函数(一维)。上式说明了二维尺度函数的可分离性。
小波变换常用于图像消噪方法为小波阈值消噪法, 其关键在于阈值的选取与估计, 基本步骤分为三步:
1) 选取适当的小波函数与分解层次对原始信号进行小波分解;
2) 对分解后得到的高频系数进行阈值量化处理;
3) 据分解变换后的低频和高频系数对二维信号图像进行重构。
2.2 小波变换法和其它图像消噪法对比二维信号图像消噪的方法分为两种: 一种是频域的方法, 在二维信号变换之后, 主要通过选择合适的频率带通滤波器对信号进行处理, 再经反变换重构信号, 例如均值滤波消噪法及中值滤波消噪法;另一种是空间域的方法, 在选取合适的图像平滑模板基础之上对图像进行卷积处理, 例如小波变化消噪法。
其中均值滤波法的基本原理是通过多个像素的平均值来代替其他像素灰度, 即将突变点的灰度分散在其相邻点中达到平滑效果, 其优点是操作简单, 但不足之处易造成图像模糊不清。
中值滤波法基本原理是选择一个活动窗口沿着图像移动, 窗口形状根据选择可采用圆形、方形或十字形等, 随后将窗口内所有像素灰度中值来代替窗口中心位置像素灰度值, 即将二维信号中某点相邻域中各点的中值代替该点的数值, 求中值的数值个数由领域的大小决定。该方法的滤波效果的好坏很大程度取决于窗口的形状与大小。
小波变换法用于二维信号消噪, 基本原理是二维信号中有用信号与噪声信号经过小波变换之后, 在不同的分辨率下呈现出不同的规律, 通过设定相应的阈值调整小波系数从而达到信号消噪的目的。
二维信号经过均值滤波处理后, 图像平滑度显著提升但图像边缘模糊度增大, 中值滤波法可以较好保护图像边缘但是易造成图像中细节损失。小波变换法在选择合适阈值前提下可以兼顾图像边缘清晰度与细节损耗。
3 二维信号消噪效果评价指标对二维信号消噪效果的评价, 需要对比客观指标来定量分析消噪后的信号相对于原始信号的好坏, 常用的评价指标有两种, 分别为峰值信噪比PSNR及模糊系数Kblur。
峰值信噪比(PSNR)是原始二维信号与经过处理之后信号之间的均方误差相对于信号最大值平方的对数值[3], 它往往通过均方误差(MSE)进行定义, 对于两个m×n的单色图像I与K, 如果它们之间噪声近似, 均方误差可表示如下:
| $ \mathrm{MSE}=\frac{1}{m \times n} \sum\limits_{i=0}^{m-1} \sum\limits_{j=0}^{n-1}[I(i, j)-K(i, j)]^{2}。$ | (2) |
则峰值信噪比的定义为:
| $ \operatorname{PSNR}=10 \times \log _{10}\left[\left(\frac{2^{n}-1}{\mathrm{MSE}}\right)\right]。$ | (3) |
其单位为dB, 数值越大代表信号失真越小, 消噪效果越好。
模糊系数为经过处理后二维信号边缘能量与原始信号边缘能量的比值, 其数学公式如下[4]:
| $ K_{b l u r}=\frac{S_{1}}{S_{2}}。$ | (4) |
S1为处理后的信号, S2为原始信号。其中边缘能量特征S的数学表达式为:
| $ S=\sum\limits_{i} \sum\limits_{j}|y(i, j, k)|_{\circ}。$ | (5) |
S为第k帧、第i行、第k列信号的亮度值经过空间滤波器处理后得到的数值。Kblur数值范围在0~1之间, 其值越接近于1, 则图像的清晰度越高。
4 MATLAB仿真实验SAR图像中, 最常见的干扰噪声为高斯白噪声与椒盐噪声, 下面通过MATLAB仿真实验, 对比不同阈值标准及噪声环境下小波去噪效果。
4.1 默认阈值消噪为分析原始信号在白噪声与椒盐噪声环境影响下, 小波变换采用不同阈值标准的适用性, 分别在原始模拟信号中加入不同类型的噪声干扰[5], 如图 2所示。
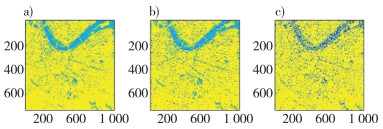 |
| 注: a)原始图像;b)添加椒盐噪声;c)添加白噪声 图 2 模拟信号加噪前后对比 |
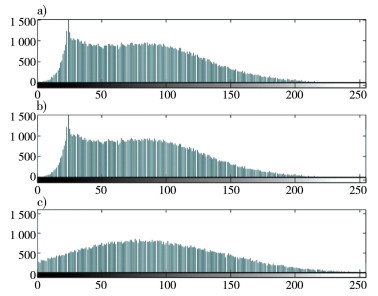 |
| 注: a)原图直方图;b)椒盐直方图;c)高斯直方图 图 3 模拟信号加噪前后直方图 |
通过生成的直方图可以清楚表明, 椒盐噪声对信号区域像素影响不大, 而高斯噪声则对信号区域像素产生显著影响, 容易掩盖信号特征。
首先对噪声信号进行默认阈值消噪, 综合考虑不同小波特性并经过反复试验, 对于模拟信号可采用sym5小波实施消噪[6]。其次明确小波分解的层数, 二维信号图像特征及采用算法决定小波分解的层数, 一般对于SAR模拟信号进行2层分解可以取得较好的消噪效果[7]。最后到得仿真结果如图 4所示。
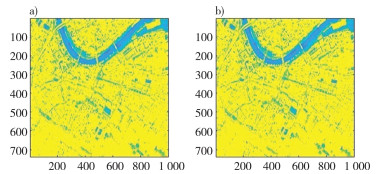 |
| 注: a)消除椒盐噪声后的图像;b)消除高斯噪声后的图像 图 4 默认阈值消噪 |
通过MATLAB实现对二维信号消噪效果指标的计算[8-10], 即计算出峰值信噪比(PSNR)与模糊系数的数值(Kblur), 经过多次计算, 取均值得到数据如表 1所示。
| 表 1 消噪效果量化评估 |
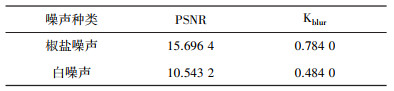 |
通过以上结果可以看出: 含有椒盐噪声的二维信号对原始图像像素分布影响不大, 图像受干扰分布较为均匀。高斯白噪声对原始图像像素分布产生较大影响且干扰分布不均匀, 较多特征点被掩盖。无论是何种类型的噪声干扰, 经过小波默认阈值法消噪处理后, 图像变的更加清晰且总体显得更加平滑。这是因为消噪过程中高频部分已被过滤掉, 即将小波分解结构中的高频系数全部置为0, 然后对信号进行重构处理[11]。重构后的消噪信号比较平滑, 但是也有可能丢失信号的有用成分。经过量化评估对比可知默认阈值消噪法消除椒盐噪声的效果明显优于消除高斯白噪声。
4.2 不同阈值标准去噪效果对比小波变换消除二维信号中噪声效果的好坏取与阈值选取的数值有关, 因此可以采用强制阈值消噪的方式处理二维信号, 选取阈值数值大小10、40、70与100分别对受椒盐噪声干扰的信号进行消噪处理, 结果图 5所示。
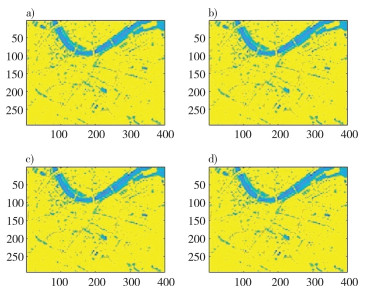 |
| 注: a)消噪后的图像thr=10;b)消噪后的图像thr=40;c)消噪后的图像thr=70;d)消噪后的图像thr=100 图 5 不同阈值大小消噪结果(椒盐噪声) |
计算不同阈值数值下, 对原始信号消噪后得到二维信号的峰值信噪比(PSNR)与模糊系数的数值(Kblur)见表 2。
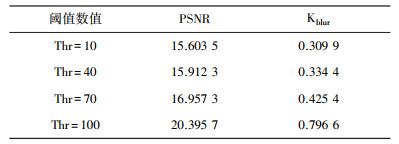
| 表 2 不同阈值数值(椒盐噪声) |
 |
接下来对受高斯白噪声干扰的信号进行相同的信号处理方式, 结果如图 6所示。
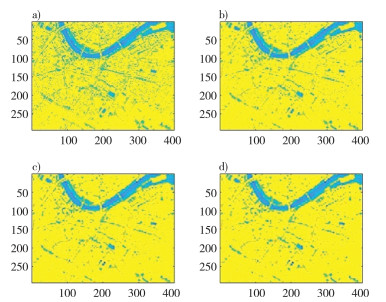 |
| 注: a)消噪后的图像thr=10;b)消噪后的图像thr=40;c)消噪后的图像thr=70;d)消噪后的图像thr=100 图 6 不同阈值大小消噪结果(高斯白噪声) |
同样可得到峰值信噪比(PSNR)与模糊系数的数值(Kblur)见表 3。
| 表 3 不同阈值数值(高斯白噪声) |
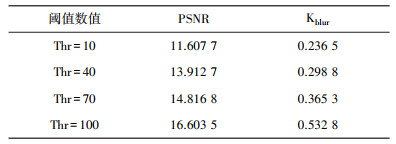 |
总结所得的图像与数据可得, 在相同阈值标准下, 相对于高斯白噪声而言, 小波变换法消噪更适合于椒盐噪声的消除, 处理后的图像更好的保留了原始二维信号的图像特征, 清晰度也相对更好。在同一种类噪声干扰的前提下, 对干扰信号选取不同数值的阈值处理, 通过对比可得, 阈值数值越小, 含噪二维信号的滤波处理越不明显, 阈值数值越大, 原始二维信号中的高频信息损失越多。
4.3 软阈值与硬阈值消噪效果对比软阈值与硬阈值是小波变换中经常选取的阈值标准, 通过以上实验结论可知, 小波变换法在处理同一种类噪声中呈现的规律是相同的且处理椒盐噪声效果相对较好, 因此可对受椒盐噪声干扰的信号分别采取软阈值与硬阈值标准的小波变换, 经过处理后对比, 得到结果如图 7。
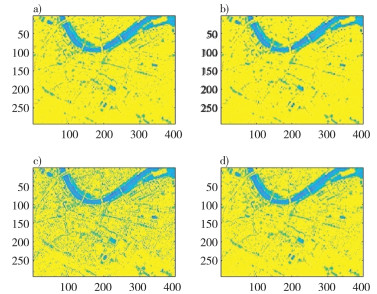 |
| 注: a)原始信号;b)软阈值消噪;c)加入噪声后的信号;d)硬阈值消噪 图 7 软、硬阈值消噪对比 |
分别计算采用软阈值与硬阈值的标准下的峰值信噪比(PSNR)与模糊系数的数值(Kblur)得到表 4。
| 表 4 软阈值与硬阈值 |
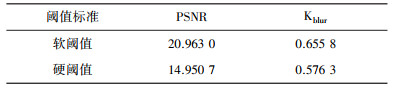 |
由图 7及表 4可知, 小波变换消噪法采用软阈值标准去除噪声的效果要好于采用硬阈值标准, 得到的图像平滑度也更佳。
5 不同阈值标准综合分析对比由以上仿真实验可得, 对干扰信号分别采取默认阈值、软阈值与硬阈值消噪处理后, 得到的结果如图 8与表 5所示。
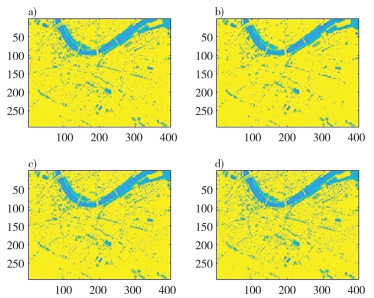 |
| 注: a)原始信号;b)软阈值消噪;c)默认阈值消噪;d)硬阈值消噪 图 8 不同阈值大小消噪结果(高斯白噪声) |
| 表 5 不同阈值标准 |
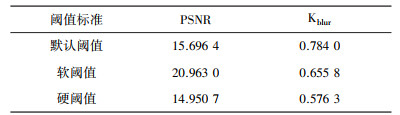 |
对于SAR图像中常见椒盐噪声和白噪声, 小波变换法更适合于消除椒盐噪声的干扰。对于不同种类的干扰, 小波变换法消噪呈现出相同的规律: 选取阈值数值大小与信号去噪效果成正比, 相应图像细节特征随着阈值数值增大而更易损耗。采用软阈值标准去噪效果明显优于默认阈值与硬阈值, 但在图像清晰度上, 默认阈值要比其他两种阈值标准更好。因此在对二维信号处理的实际应用中, 若对图像细节特征要求不高而对信号强度有要求时, 可采用软阈值消噪, 若对图像细节特征有一定要求时, 可采用默认阈值消噪, 通过牺牲信号强度保留图像细节特征。
6 结束语本文分析了SAR图像处理与二维信号小波变换的基本原理, 提出将小波变换应用于SAR图像处理的思路, 通过MATLAB仿真实验研究小波变换对常见噪声处理效果及采用不同阈值标准所呈现的规律, 进行定量分析, 对实际应用中SAR图像处理可采取的小波变换阈值选择标准进行归纳总结。
| [1] |
计科峰. SAR图像目标特征提取与分类方法研究[D]. 长沙: 国防科技大学, 2003.
|
| [2] |
张红, 王超, 张波. 高分辨率SAR图像目标识别[M]. 北京: 科学出版社, 2009.
|
| [3] |
袁飞, 黄连芬, 姚彦. 视频质量客观评价技术研究标准[J]. 检测与仪器, 2007, 31(3): 91-94. DOI:10.3969/j.issn.1002-8692.2007.03.033 |
| [4] |
黄文辉, 陈仁雷, 张家谋. 数字视频图像质量客观方法的改进与实现[J]. 北京邮电大学学报, 2005, 28(4): 87-90. |
| [5] |
王俊卿, 黄莎白, 史泽林, 等. 基于小波变换的图像边缘检测[J]. 系统工程与电子技术, 2004(7): 887-889. DOI:10.3321/j.issn:1001-506X.2004.07.010 |
| [6] |
程正兴. 小波分析算法与应用[M]. 西安: 西安交通大学出版社, 1998.
|
| [7] |
邱庚香, 陈德海. 基于小波变换的信号去噪应用[J]. 江西理工大学学报, 2003, 24(4): 13. |
| [8] |
张兆礼. 现代图像处理技术及Matlab实现[M]. 北京: 人民邮电出版社, 2001.
|
| [9] |
张志涌. 精通Matlab6. 第5版[M]. 北京: 北京航空航天大学出版社, 2003.
|
| [10] |
王家文, 曹宇. Matlab6.5图形图像处理[M]. 北京: 国防工业出版社, 2004.
|
| [11] |
JUNYA LV, YUE LIU. Dataaugmentation based on attributed scattering centers to train robust cnn for sar atr[J]. IEEE Access, 2019, 10(5): 12-15. |
 2021, Vol. 35
2021, Vol. 35

