| 基于多元回归全球气候变化的模型分析 |
全球变暖是指全球气温升高。是由于温室效应不断累增, 进而导致地热系统吸收和发射能量不平衡, 能量进一步累积, 致使全球气温升高, 导致全球变暖。这与人类活动密切相关, 由于人们焚烧化石燃料, 如石油, 煤炭等, 或砍伐森林并将其焚烧时会产生大量的二氧化碳, 即温室气体, 这些温室气体对来自太阳辐射的可见光具有高度透过性, 而对地球发射出来的长波辐射具有高度吸收性, 能强烈吸收地面辐射中的红外线, 导致地球温度上升, 即温室效应。目前在国际社会中, 全球变暖俨然成为各领域科学家关注的焦点。同时全球变暖也给全球带来许多风险, 冰川融化、海平面上升以及一些极端天气的出现, 这无疑是人类所共同面临的挑战。但从大量观测资料发现, 自21世纪以来, 全球年平均表面温度的增温速率明显偏低, 仅为0.03 ℃, 发生了Hiatus(全球变暖停滞状态)[1]。
全球变暖停滞的发生, 加之2019年1月美国三分之二的地区出现了极度寒冷天气, 使得全球变暖现象被质疑。不仅如此, 海洋吸收热量对全球气候变化的影响很大。其中还夹杂着许多其他的因素, 海洋表面温度的变化具有某种震荡的特性, 如厄尔尼诺现象、拉尼娜现象等。这些因素对全球温度变化的研究造成了不小的困难。
1 问题的建模与求解 1.1 对于未来几年气候变化预测对未来几年气候变化进行相应预测, 利用多元线性回归进行求解是一种好的处理方法, 考虑到对未来进行预测, 这对模型预测以及数据处理要求很高, 所以运用stepwise regression方法进行逐步求解是最有效的回归模型。考虑到气候的变化要受多因素的影响, 主要包括地球的吸热放热(主要考虑长波短波因素)、海洋表面温度、CO2浓度、地球表面植被以及人类活动等影响因素[2]。考虑了新增影响因子对已有变量的影响, 同时剔除了一些无关变量对整体模型的影响, 留下有效变量, 以便于求解多变量的多元线性回归模型。
考虑到影响温度变化的全部变量, 利用逐步回归的方法, 选择对影响气温的显著变量建立模型。为了简要说明这个模型, 下面选取了4个解释变量, 研究平均温度为Y, 解释变量:X1CO2浓度、X2地球的吸热、X3地球的放热(主要考虑长波短波因素)、X4海洋表面温度, 其中β0, β1, β2, β3, β4为相应系数。以全球平均温度为因变量, 以如上4个解释变量为自变量做多元线性回归。由于加入其他变量也是利用逐步回归的方法也是一样, 因此我们这里将其余因素设为无关变量。由于数据庞大且复杂, 因此通过分析经纬度这里单独抽取出了世界某处具有代表性的点, 并对其进行了线性回归性分析。
通过SPSS在sst.mnmean.nc网站中提取的相应的123个数据做相关分析, 其中相关数据都是提取近100年来的数据取得均值, 具有一定的代表性, 从中剔除无关数据, 保留有用数据。进而给出相关性检验, 下表给出相关性检验:
| 表 1 相关性检验 |
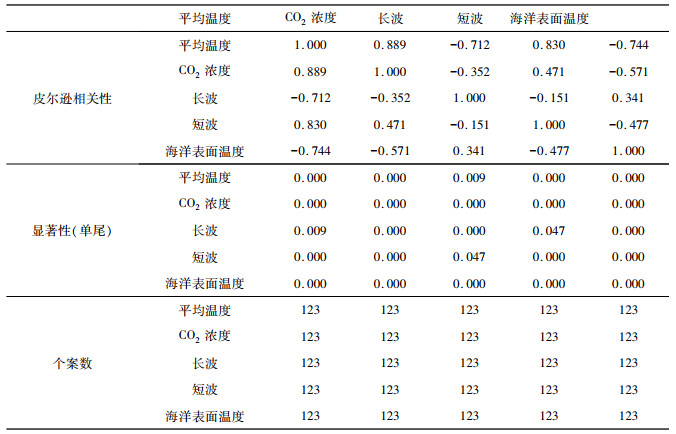 |
通过SPSS做变量的相关分析, 可以看出Y与自变量的相关系数大多都在0.7以上, 说明所选择变量与Y高度线性相关, 所以用Y与自变量做多元线性回归是合适的。且观察相关变量与平均温度的散点图更好说明其相关性。散点图如下:
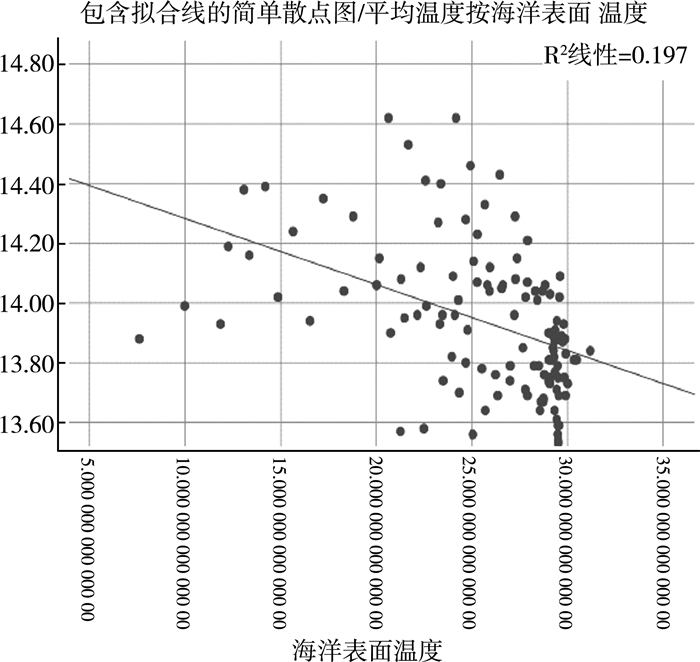 |
| 图 1 平均温度与海洋表面温度 |
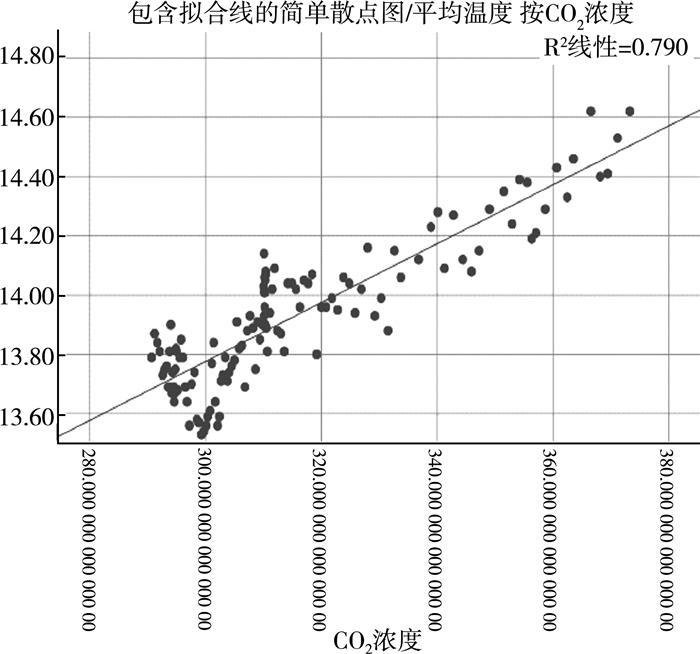 |
| 图 2 平均温度与CO2浓度 |
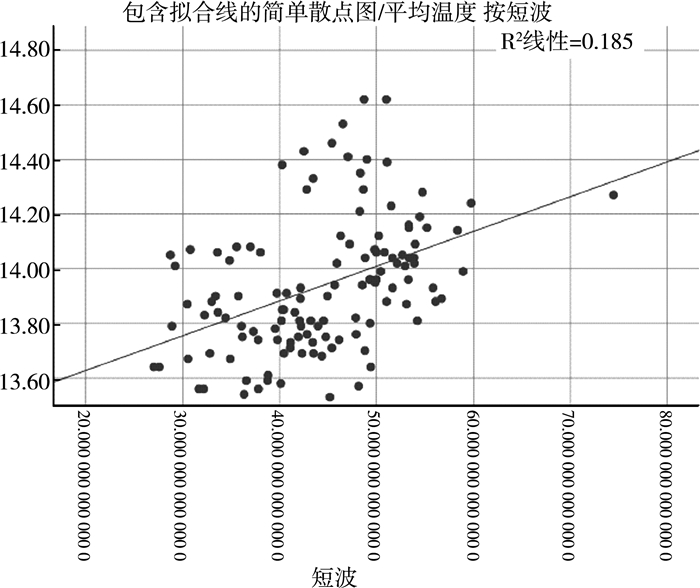 |
| 图 3 平均温度与短波 |
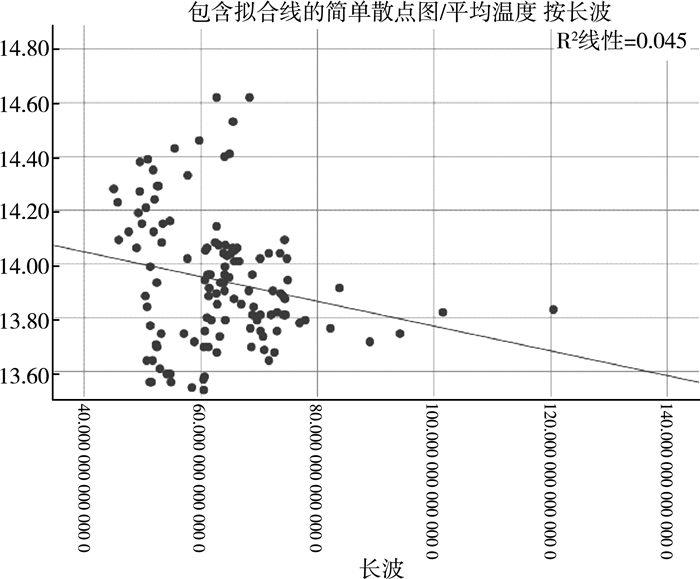 |
| 图 4 平均温度与长波 |
通过系数相关性大小以及散点图判定可知得到全球平均温度与海洋表面温度、CO2浓度、地球吸放热(长波、短波)有着明显相关性。观察数据可知几个相关变量的显著性都是0是小于0.001的, 说明几个相关变量显著性较好。因为样本受多个因素影响, 且各个因素都与气温指数呈现相应的线性关系, 进而可以利用多元回归方程来观察各因素对气温影响的强弱[3]。
从表 2中发现F=122.267, 说明4个自变量整体对因变量Y产生显著线性影响。
| 表 2 变异数分析 |
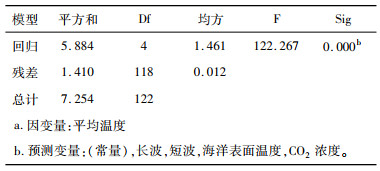 |
可根据上述两表中发现四个解释变量对于平均温度影响显著, 可以通过检验的回归系数, 进而这四个解释变量可以跟因变量建立回归方程。而且地球的吸热、海洋表面温度、CO2浓度起正影响而地球的吸热却对平均温度起负影响, 与常识相违背, 因此可能存在多重共线性。
应用SPSS进行异方差性检验。用斯皮尔曼相关系数检验异方差性也就是检验随机误差项的方差与解释变量观测值之间的相关性。若相关系数较高, 则存在异方差性, 则不能通过异方差性检验, 此时可能会导致参数OLS估计的方差增大, 根据图形分析:
根据图 5-图 7分析可知, 残差是服从正态分布的, p-p图中散点均匀分布在对角线且散点图呈不规则图形没有特定规律, 进而不能认为残差绝对值与解释变量显著相关。所以不存在异方差性。对数据进行处理可得到以下线性方程:
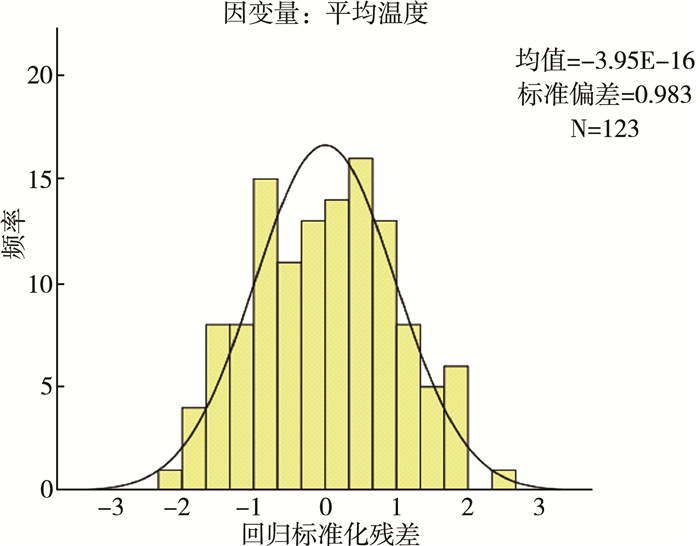 |
| 图 5 直方图 |
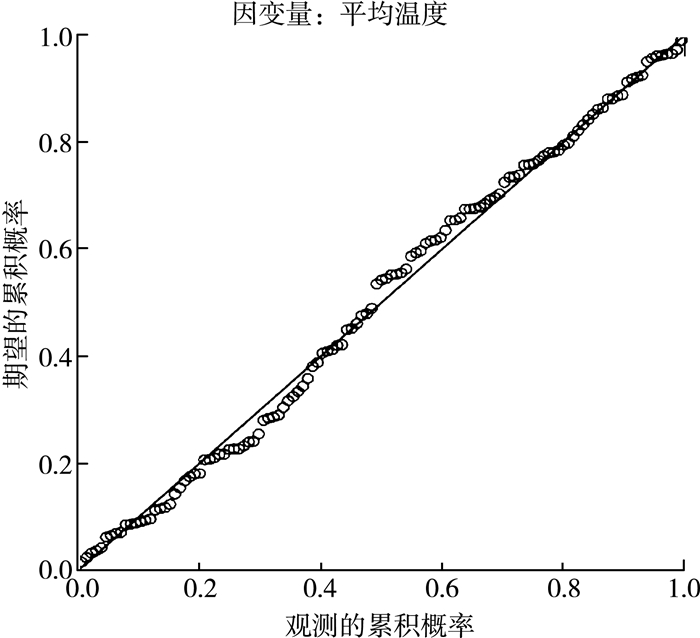 |
| 图 6 标准P-P图 |
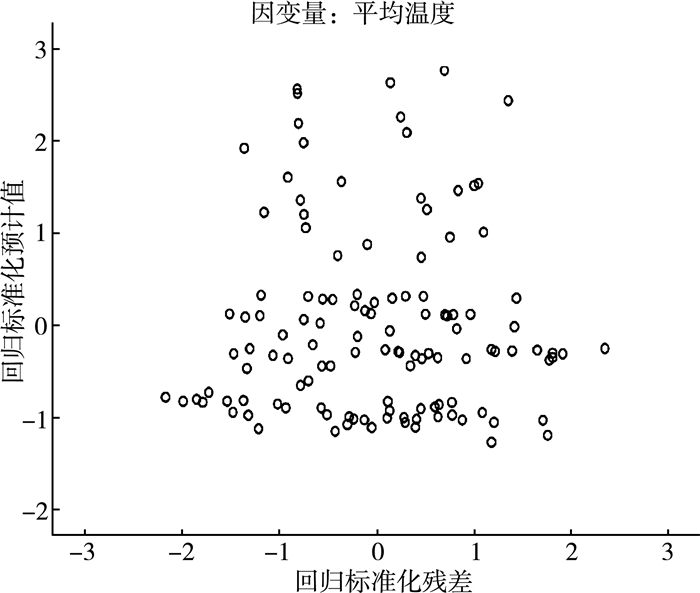 |
| 图 7 散点图 |
| $ \left\{\begin{array}{l} \text { 13. 79 }=\beta_{0}+290.7 \beta_{1}+61.787 \beta_{2}+ \text { 28. } 8972 \beta_{3}+29.476 \beta_{4} \\ \text { 13. } 87=\beta_{0}+291.2 \beta_{1}+65.661 \beta_{2}+ \text { 30. } 469 \beta_{3}+29.741 \beta_{4} \\ \text { 13. } 84=\beta_{0}+290.7 \beta_{1}+69.013 \beta_{2}+ \text { 41. } 5621 \beta_{3}+31.186 \beta_{4} \\ \text { .. } \\ \text { 14. } 62=\beta_{0}+373.2 \beta_{1}+68.3322 \beta_{2}+ \text { 51. } 016 \beta_{3}+20.641 \beta_{4} \end{array}\right. $ | (1) |
可通过SPSS进行的回归分析并求解进而可求得相应的多元回归方程为:
| $ \begin{array}{c} Y=12.11052+1.354541 X_{1}+ \\ 1.568431 X_{2}+3.174641 X_{3}-2.6414 X_{4} \end{array} $ | (2) |
对于模型求解可得到了多元线性回归方程, 可知地球放热对于温度影响最大, 其次CO2浓度对温度影响也较大, 通过观察回归方程可以推出随着时间推移全球CO2浓度会随之升高, 这其中包括人类活动、植被量的减少之间影响CO2浓度, 进而X1会呈现上升趋势, 随着时间变化地球放热量上升, 吸收热量下降, 即X2、X3会呈现一个上升一个下降趋势, 海洋表面温度X4也会随着时间推移逐渐下降。
影响气候变化的因素主要有温度、降雨量、空气湿度等, 其中降雨量以及空气湿度也主要受海洋表表面温度、CO2浓度、地球吸放热(长波、短波)的影响, 进而降雨量、空气湿度两要素也可以类似温度建立同类型的多元回归模型, 这里只考虑了温度的要素, 其余的要素也跟温度类似, 所以没有对其余两要素一一建模。同时其余要素也跟温度成类似的变化趋势, 进而主要阐述关于温度的多元线性回归模型[4]。
经对于回归方程在未来几年中的一系列数据的分析以及对数据相应处理, 可知X1、X2会有上升趋势, X3、X4会有下降趋势, 全球平均温度Y会呈现上升趋势, 根据回归方程多变量的影响因素可判定对于未来几年气候主要变化为温度呈现上升趋势, 降雨量会相应减少, 同时空气湿度会降低, 根据数据分析在未来几年的讨论的相关影响因素变化也会跟平均温度呈现线性关系, 进而未来几年全球主要呈现变暖趋势。
1.2 极端天气与气候变化的关系在两极地区, 由于纬度高, 是全球温度最低的区域, 所以在两极地区的近地面会由于低温而使得空气冷却下沉, 在近地面形成高气压, 被称之为“极地高气压带”, 在近地面空气会从极地高压向四周流出, 形成冷空气向低纬入侵。不仅如此, 极地地区的冷空气还在不断的旋转之中, 形成“极地涡旋”, 南极地区的极地涡旋势力通常更为强大[5]。
极地涡旋:它指的是环绕着地球两极的大面积冷空气和低压, 在冬季涡旋会扩展到北半球, 会将冷空气推向更南方, 极地涡旋带来的最大危险是温度急剧下降, 特别是在不常有寒冷天气的地区[6]。
根据SPSS对极寒天气以及多个因素变量, 提取相应数据做回归分析, 观察变量与极寒温度之间的关系, 得到图表数据如下:
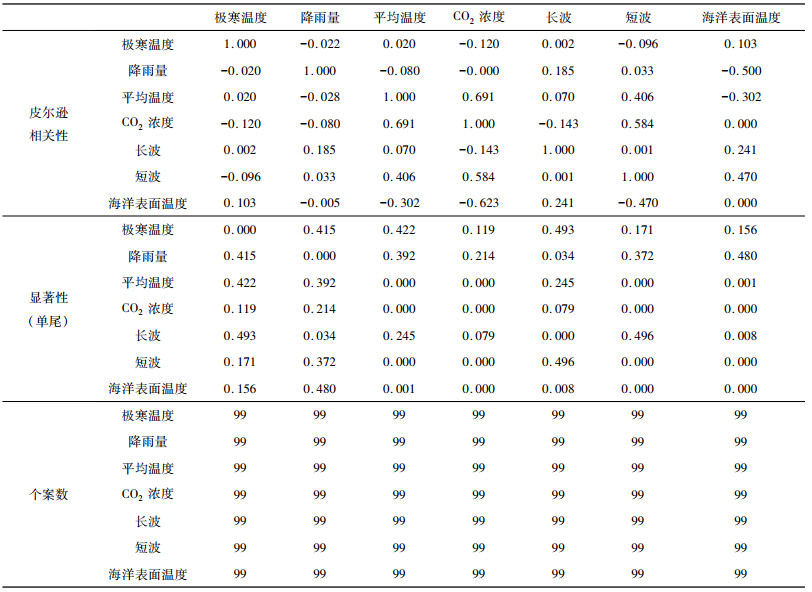
表 3给出的皮尔逊相关系数和显著性回归分析可得到极寒温度与全球平均气温、降雨量、CO2浓度、地球吸放热(长波, 短波)以及海洋表面温度存在明显的相关性, 以便更好说明这些变量与极寒温度的关系。通过对做出的散点图进行分析, 观察它们是否有线性性。散点图如下:
| 表 3 相关性检验 |
 |
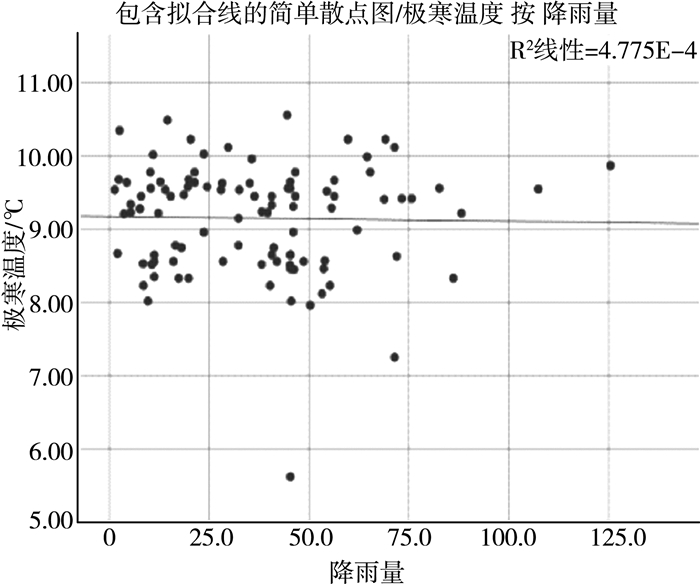 |
| 图 8 极寒温度与平均温度 |
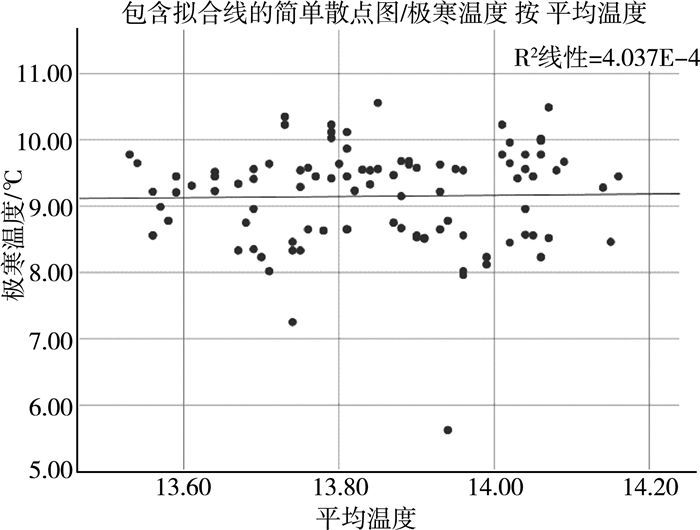 |
| 图 9 极寒温度与降雨量 |
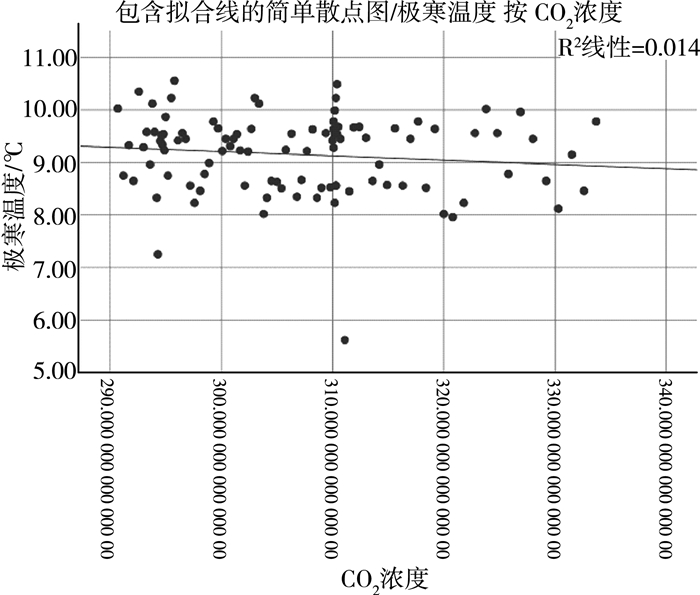 |
| 图 10 极寒温度与CO2浓度 |
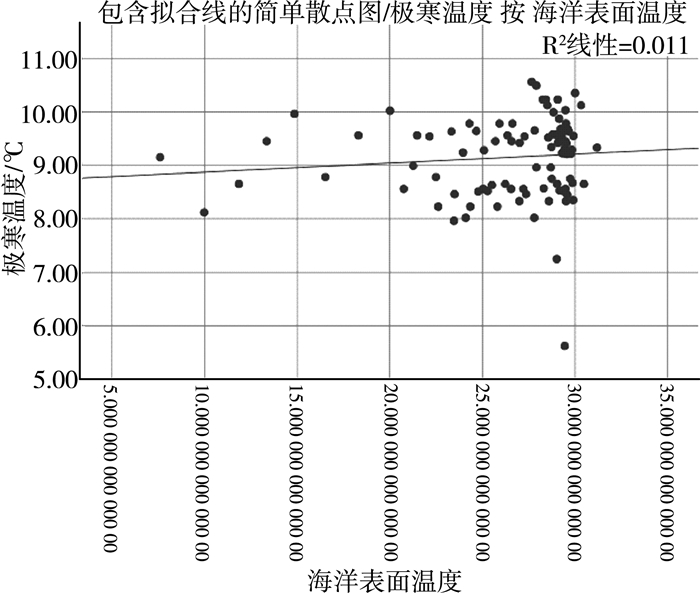 |
| 图 11 极寒温度与海洋表面温度 |
分析散点图可以得到这些相关因素与极寒温度存在明显的线性关系, 所以可以通过多元线性回归模型来说明极寒天气与相关变量的关系。由于极寒温度以及多个因素影响, 且单个因素对其影响强弱不同, 包含正相关与负相关之分, 为了更容易观察极寒温度呈现的趋势, 选取6个解释变量, 研究极寒温度为Z, 解释变量:X1地球的吸热、X2地球的放热(主要考虑长波短波因素)、X3海洋表面温度、X4CO2浓度、y1全球平均温度、y2降雨量, 其中α0, α1, α2, α3, α4, α5, α6为相应系数[7]。以极寒温度为因变量, 以如上6个解释变量为自变量做多元线性回归。下面通过SPSS进行分析可知极寒温度与6个解释变量呈现相应线性关系, 进而利用线性回归来求解。
经过数据处理可得到以下线性方程组:
| $ \left\{\begin{array}{l} 10. 03=\alpha_{0}+13.79 \alpha_{1}+23.6 \alpha_{2}+ \\ ~~~290. 7 \alpha_{3}+61.79 \alpha_{4}+28.88 \alpha_{5}+ \\ ~~~29. 48 \alpha_{6} \\ 8. 75=\alpha_{0}+13.87 \alpha_{1}+41.1 \alpha_{2}+ \\ ~~~291. 2 \alpha_{3}+65.66 \alpha_{4}+30.47 \alpha_{5}+ \\ ~~~29. 74 \alpha_{6} \\ 9. 33=\alpha_{0}+13.84 \alpha_{1}+40.6 \alpha_{2}+ \\ ~~~291. 7 \alpha_{3}+69.01 \alpha_{4}+41.56 \alpha_{5}+ \\ ~~~31. 19 \alpha_{6}\\ 8.65=\alpha_{0}+13.81 \alpha_{1}+11.2 \alpha_{2}+ \\ ~~~292.1 \alpha_{3}+70.18 \alpha_{4}+43.22 \alpha_{5}+ \\ ~~~30.47 \alpha_{6} \\ 10.35=\alpha_{0}+13.73 \alpha_{1}+2.5 \alpha_{2}+ \\ ~~~292.6 \alpha_{3}+70.65 \alpha_{4}+53.334 \alpha_{5}+ \\ ~~~29.99 \alpha_{6} \\ \cdots ~~~~~~~~~~~ \ldots\\ 8.46=\alpha_{0}+14.15 \alpha_{1}+45.3 \alpha_{2}+\\ ~~~332. 6 \alpha_{3}+49.87 \alpha_{4}+53.33 \alpha_{5}+ \\ ~~~27. 35 \alpha_{6} \\ 9. 78=\alpha_{0}+14.06 \alpha_{1}+21.3 \alpha_{2}+ \\ ~~~333. 7 \alpha_{3}+48.96 \alpha_{4}+50.82 \alpha_{5}+ \\ ~~~26. 62 \alpha_{6} \end{array}\right. $ | (3) |
通过SPSS系数求解可以得到以下多元回归方程, 当然其中也会包含误差这里用ε0来说明方程如下:
| $ \begin{array}{c} Z=3.2897+2.5764 y_{1}+0.51914 y_{2}+1 . \\ 3611 X_{1}-0.5621 X_{2}-0.4324 X_{3}+0.910 X_{4}+\varepsilon_{0} \end{array} $ | (4) |
对于得到的多元回归模型可以分析可得极寒天气Z易受全球温度y1变化的影响, 随着全球温度y1的升高, 可得极寒温度Z会呈现上升趋势, 当然极寒天气也会受到其它因素的影响。进而推出全球变暖与极寒现象的出现不会存在矛盾[8]。
2 模型推广本文依据题目所给出的多个变量数据和相关资料, 对于分析多因素影响气候变化运用了多元回归模型, 此模型更加简单和方便, 通过最后的结果可以看出, 文中建立的这个模型的可靠性是比较高的。文中所提到的模型, 应用性极强, 应用范围广, 可以把此模型推广到极热天气出现和气候变化是否有关系或某种极端天气的预测上。
| [1] |
MEEHL G.A., HU A., SANTER B.D.S, et al. Contribution of the interdecadal pacific oscillation to twentie th-century global surface temperature tend[J]. Nature Climate Change, 2016, 6(11): 1005-1008. |
| [2] |
ZEYUAN HU, AIXUE HU, YONGYUN HU. Contri butions of interdecadal pacific oscillation and atlantic multidecadal oscillation to global ocean heat content di stribution[J]. Journal of Climate, 2018, 31(3): 1227-1244. |
| [3] |
郑益之, 陈幸荣, 蔡怡. 全球变暖背景下基于Non-Bo ussinesq POP模式对海平面高度的模拟和预估[J]. 海洋预报, 2018, 35(06): 58-65. |
| [4] |
BROWN B.E., DUNNE R.P., SOMERFIELD P.J., et al. Long-term impacts of rising sea temperature and sea level on shallow water coral communities over a~40 year period[J]. Scientific Reports, 2019, 9(1): 1-12. |
| [5] |
苏京志, 温敏, 丁一汇, 等. 全球变暖趋缓研究进展[J]. 大气科学, 2016, 40(06): 1143-1153. |
| [6] |
孟庆佳, 林鹏飞, 唐晓晖. 20世纪热带海洋海表面温度年际变化的特征[J]. 海洋科学, 2015, 39(03): 59-65. |
| [7] |
章杰, 鱼京善, 来文立. 全球变暖背景下极端降水变化率与气温的响应关系[J]. 北京师范大学学报(自然科学版), 2017, 53(06): 722-726. |
| [8] |
燕青, 张仲石, 王会军, 等. 上新世中期海洋表面温度变化及其与古气候重建数据对比[J]. 科学通报, 2011, 56(06): 423-432. |
 2020, Vol. 34
2020, Vol. 34


