| 面向多源数据融合的贝叶斯估计方法 |
近年来,数据融合技术的理论和方法在各个领域得到了广泛的应用和发展。另外,各种数据融合研究组织以及相关的年会也为它的应用和技术提供了深入的研讨。当前,多传感器数据融合技术[1]已经广泛应用于军事、航天、智能机器人控制等领域,其理论与方法已成为智能信息处理的一个重要研究领域。数据融合技术是多源信息的一种处理方法,它起源于军事领域中的多传感器综合应用,又叫多传感器数据融合(或多源数据融合)[2]。传感器是数据的主要来源。传感器不一定是物理形式的,数据源或者信息源甚至人工数据都可以称为传感器。多源数据融合实际上比单个数据源更具优势。数据融合技术是对多源数据优化处理[3]的多种方法的统称。数据融合技术为分析、估计和校准不同形式的信息,适应海量数据处理的需要、同时利用这些信息进行正确的决策评估提供了可能。
多源数据融合指将同一目标的多个观测结果归入一个统一的结果,用以取代多个观测结果,即将信息从多个数据源融合为统一模式的技术。数据融合系统广泛应用于传感器网络、机器人、视频图像处理和智能系统设计等领域[4]。简单说就是多种数据的综合算法处理的目的是将获得的信息进行关联、相关及识别,并据此作出决策和评估。通过多源数据融合,可以增加置信度、减少模糊性、提高系统可靠性。多传感器系统首要的目标是将来自多个传感器的测量数据及相关数据库的有关信息进行关联、相关等以获得更加全面、可靠的数据信息[5]。然而来自多传感器的数据会遇到许多问题,比如数据的相关,传感器不确定性和环境因素等,而最根本的问题在于传感器测量系统中固有的不确定性。这种不确定性的出现不仅来自测量的不精确性,还来自于各个传感器的不稳定性、不一致性。通过基于贝叶斯估计的多源数据融合方法,进行数据处理,对现有的国内外研究成果进行了学习研究,最后通过实验表明该方法确实有效。
1 国内外研究概述随着电子信息技术的快速发展,数据处理的技术——数据融合也得到了广泛地应用与发展。文献[6]讨论了现有的数据融合方法的优缺点,并研究了在每一种方法的基础上解决特定数据相关、具有挑战性的方面。文中针对测量数据的不一致性,主要是模拟了这种不一致性,融合不同类型的数据来得到数据的一致性。文献[7]系统地论述了Bayes算法的基本思想,结合数据融合过程的需求,从中归纳出该算法存在的局限性,避免这些局限性影响数据融合效果。表明采用Bayes估计算法可以有效地对多源不确定性数据进行融合,并可以适应融合随时间、空间变化的数据需求。文献[8]主要是在工业领域中针对高炉料面检测中多传感器数据难以直接应用的问题,把理论料形与多源数据Bayes融合,使得检测更加精准,为高炉节能减排操作提供了必要的指导。文献[9]提出了一种基于贝叶斯方法的传感器融合策略,可以识别在传感器数据中的不一致性,使杂乱的数据从传感器融合过程中消除。
在多源数据融合系统中,由于噪声或者其他因素破坏了信号中原有的一部分数据,并且无法在以后的处理中提取还原噪声中的原始数据,加之信号本身也不可能包含观测对象的完整信息,导致多传感器提供的数据可能不完整、不精确,包含着大量的不确定性和不一致性。这些因素使数据融合系统无法获得完整、精确的数据。利用贝叶斯估计算法可以有效地对多源不确定性、不一致性数据进行融合,从实质上识别传感器数据的不一致,从而反映所测数据的真实状态。
2 贝叶斯估计 2.1 基本概念贝叶斯理论是英国数学家Thomas Bayes提出的[10],在1764年发表在伦敦皇家学会哲学会刊上的贝叶斯遗稿《机遇理论中一个问题的解》中就包含了贝叶斯公式,贝叶斯对统计推理的主要贡献是使用了“逆概率”这个概念,并把它作为一种普遍的推理方法提出来。贝叶斯估计理论[11]的主要思想是假定要估计的模型参数服从一定分布的随机变量,根据经验给出待估参数的先验分布(也称为主观分布),关于这些先验分布的信息被称为先验信息;然后根据这些先验信息,并与样本信息相结合,应用贝叶斯定理求出待估参数的后验信息;然后得出后验分布的一些特征值,并把它们作为待估参数的估计量。概括的讲就是将关于未知参数的先验信息与样本信息综合,再根据贝叶斯定理,得出后验信息,最后根据后验信息去推断未知参数。贝叶斯估计过程[12]如图 1所示。
 |
| 图 1 贝叶斯估计的推理过程 |
贝叶斯估计[13],设总体X的分布函数F(x, θ),θ为随机变量,p(θ)为θ的先验分布。若是在决策空间D中存在一个决策函数d*(X),使得对决策空间D中任一决策函数d(X),均有:
| $ R\left( {{d^ * }} \right) = \mathop {\inf }\limits_d R\left( d \right),\forall d \in D\left( {下确界} \right), $ | (1) |
则称d*(X)为参数θ的贝叶斯估计量。其中R(d)称为决策函数d*(X)的贝叶斯风险。贝叶斯估计量依赖于先验分布p(θ),即对于不同的p(θ),θ的贝叶斯估计量是不同的。
若给定θ的先验分布p(θ)和平方损失函数:
| $ L\left( {\theta ,d} \right) = {\left( {\theta - d} \right)^2}, $ | (2) |
则θ的贝叶斯估计为:
| $ d\left( x \right) = E\left( {\theta \left| {X = x} \right.} \right) = \int_\theta {\theta p\left( {\theta \left| x \right.} \right)d\theta } , $ | (3) |
其中p(θ|x)为参数θ的后验概率。
2.2 贝叶斯估计算法贝叶斯估计算法[14]和传统方法的主要区别在于是否融合了先验信息和样本信息。贝叶斯估计把待估计的参数看成是符合某种先验概率分布的随机变量;对样本进行观测的过程,就是把先验概率密度转化为后验概率密度,这样就利用样本的信息修正了对参数的初始估计值。
假设在作出观测之前,状态X的信息是独立可用的,则关于X的先验信息可以被概括为先验概率P(X)。贝叶斯定理提供了X的后验条件分布,给出了Z,贝叶斯公式提供了从先验概率P(X)、p(Z)和概率密度函数P(Z|X)计算后验概率的方法:
| $ p\left( {X\left| Z \right.} \right) = \frac{{p\left( {X\left| Z \right.} \right)P\left( X \right)}}{{P\left( Z \right)}}。$ | (4) |
p(X|Z)随着P(X)和P(Z|X)的增长而增长,随着p(Z)的增长而减少。如果Z独立于X时被观察到的可能性越大,那么Z对X的支持度越小。
最大后验估计(MAP):后验估计与先验概率和似然函数之积是成一定比例的,即通过最大化(4)的分子得到:
| $ {{\hat x}_{MAP}} = \arg \max p\left( {X\left| Z \right.} \right) \propto p\left( {X\left| Z \right.} \right)P\left( X \right)。$ | (5) |
由传感器提供的信息通常建模为一个近似于真实值的平均值,概率传感器模型可使测定所获得数据的统计特征更容易[15]。在已知测定量X(即给定样本集)状态的条件下,这个概率模型能够得到传感器Z的概率分布。该分布是针对具体的某个传感器,而且能够通过实验来确定,因此p(Z|X)也服从正态分布。正态分布是一种最常用表示传感器不确定性的分布:
| $ p\left( {Z = {z_s}\left| X \right.} \right) = \frac{1}{{{\sigma _s}\sqrt {2\pi } }}\exp \left\{ { - \frac{1}{2}\frac{{{{\left( {x - {z_s}} \right)}^2}}}{{\sigma _s^2}}} \right\}。$ | (6) |
标准偏差的分布σ是由传感器提供的数据的不确定性的度量。S代表第S个传感器,如果有两个传感器模型[16-18](即S=1, 2)都由上式正态似然函数给出,则从贝叶斯定理中可知,融合的最大后验(MAP)估计为:
| $ \begin{array}{l} {x_{MAP}} = \arg \max \left[ {p\left( {Z = {z_1}\left| {X = x} \right.} \right)p\left( {Z = {z_2}\left| {X = x} \right.} \right)} \right]\\ {x_{MAP}} = \arg \max \left[ {\frac{1}{{{\sigma _1}{\sigma _2}2\pi }}\exp - \left\{ {\frac{{{{\left( {x - {z_1}} \right)}^2}}}{{\sigma _1^2}} + \frac{{{{\left( {x - {z_2}} \right)}^2}}}{{\sigma _2^2}}} \right\}} \right]。\end{array} $ | (7) |
由此给出:
| $ \begin{array}{l} {x_{MAP}} = \frac{{\sigma _2^2}}{{\sigma _1^2 + \sigma _2^2}}{z_1} + \frac{{\sigma _1^2}}{{\sigma _1^2 + \sigma _2^2}}{z_2}\\ \;\;\;\;\;\;\; = \frac{1}{{{r^2} + 1}}{z_1} + \frac{1}{{\frac{1}{{{r^2}}} + 1}}{z_2}。\end{array} $ | (8) |
| $ \sigma _v^2 = \frac{{\sigma _1^2 \cdot \sigma _2^2}}{{\sigma _1^2 + \sigma _2^2}} = 1/\left[ {\left( {{\sigma _1}} \right) - 2 + \left( {{\sigma _2}} \right) - 2} \right]。$ | (9) |
在一些工业环境中,由于传感器故障,或者传感器的一些固有的局限性以及环境中的某些因素,传感器经常提供不准确或者不一致的数据。下面对数据测量的不一致性提出一种改进[9]:
| $ \begin{array}{l} p\left( {X\left| {Z = {z_1},{z_2}} \right.} \right) \propto \frac{1}{{{\sigma _1}\sqrt {2\pi } }}\exp - \frac{{{{\left( {x - {z_1}} \right)}^2}}}{{2\sigma _1^2Fac}} \times \\ \frac{1}{{{\sigma _2}\sqrt {2\pi } }}\exp - \frac{{{{\left( {x - {z_1}} \right)}^2}}}{{2\sigma _2^2Fac}}。\end{array} $ | (10) |
可以看出改进后,增加了因子Fac:
Input:σ1, σ2, z1, z2, xs, ps
Output:xMAP, σv2
过程:1)先求标准偏差的比:r=σ1/σ2;
2) s表示传感器数量,用两个传感器进行测量,所以s←1 to 2;
3) xs, Ps;//测量得到的值;
4) XMAP←x1/(r2+1)+x2/(r-2+1);
5) 根据
6) 融合方差σv2←1/(σ1-2, Fac-1+σ2-2, Fac-1)。
2.5 实验分析 2.5.1 实验数据数据来自于UCI数据库的Sensorless drive diagno sis,是通过2个传感器采样速度为2 000次/s采集的数据。
2.5.2 数据融合后的仿真结果数据与贝叶斯估计方法融合,仿真结果如图 2所示。
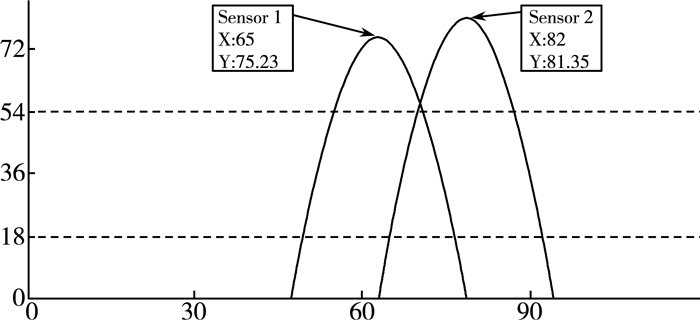 |
| 图 2 数据融合后的仿真结果 |
2.5.3 贝叶斯估计与其他方法的比较
将贝叶斯估计与下限值法、Schoute估计法、空闲时隙数法以及Vogt估计法通过MATLAB仿真进行相对误差比较,结果如图 3所示。从图中可以明显看出贝叶斯估计法的相对误差是最低的。
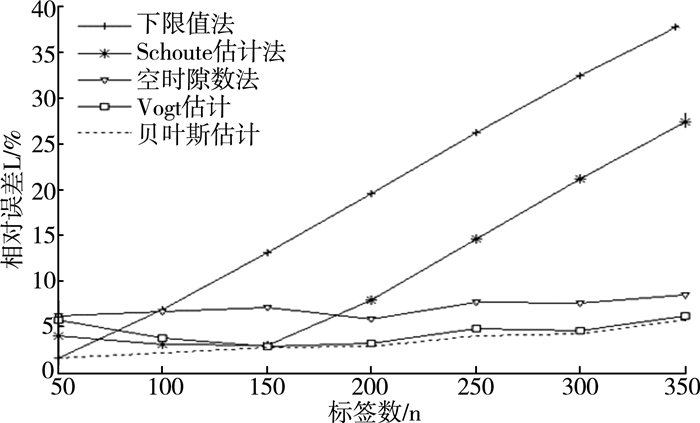 |
| 图 3 不同算法的比较 |
3 结语
多传感器所测得数据具有不确定性和不一致性,故采用贝叶斯估计法对多源数据(即多传感器数据)进行处理。实验证明采用贝叶斯估计算法可以有效地对多源不确定性数据进行融合,从根本上解决传感器数据的不一致,使所测数据能够更加完整、精确。不足之处是贝叶斯估计是利用参数的先验分布进行推断的一种方法,但是要找到一个合适的先验分布并不容易。
| [1] |
黄漫国, 樊尚春, 郑德智, 等. 多传感器数据融合技术研究进展[J]. 传感器与微系统, 2010, 29(3): 5-8. |
| [2] |
刘同明, 夏祖勋, 解洪成. 数据融合技术及其应用[M]. 北京: 国防工业出版社, 2000.
|
| [3] |
袁金国, 王卫. 多源遥感数据融合应用研究[J]. 地球信息科学, 2005, 7(3): 97-99. |
| [4] |
滕召胜, 罗隆福, 童调生. 智能检测系统与数据融合[M]. 北京: 机械工业出版社, 2000.
|
| [5] |
张铁壁. 多传感器数据融合技术在智能压力检测中的应用[J]. 河北工程技术高等专科学校学报, 2003(6): 26-29. |
| [6] |
BAHADOR K, ALAA K, FALCHREDDINE O K. Multisensor data fusion:A review of the state-of-the-art[J]. Information Fusion, 2011(8): 1-14. |
| [7] |
商娟叶. 基于数据融合的Bayes估计算法研究[J]. 自动化与仪器仪表, 2016(2): 118-120. |
| [8] |
苗亮亮, 陈先中, 侯庆文, 等. 高炉料面检测中的多源数据融合[J]. 光学精密工程, 2014, 22(9): 2407-2414. |
| [9] |
MANISH K, DEVENDRA P G, RANDY A Z. A generalized approach for inconsistency detection in data fusion from multiple sensors[J]. 2006 IEEE American Control Conference, 2006(1): 2078-2081. |
| [10] |
DALE A I. Most honorable remembrance:the life and work of thomas bayes[M]. New York: Berlin-Heidelberg, 2003.
|
| [11] |
AMINI K, BOSTAN E, UNSER M. Bayesian estimation for continuous-time sparse stochastic processes[J]. IEEE Transactions on Signal Processing, 2013, 61(4): 907-919. DOI:10.1109/TSP.2012.2226446 |
| [12] |
张瑞. 基于贝叶斯估计的视觉跟踪算法研究[D]. 福州: 福建师范大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10394-1015719739.htm
|
| [13] |
李贤平, 沈崇圣, 陈子毅. 概率论与数理统计[M]. 上海: 复旦大学出版社, 2003, 98-100.
|
| [14] |
宁永成, 侯代文. 递推的贝叶斯估计方法[J]. 四川兵工学报, 2013, 34(10): 130-136. |
| [15] |
张品, 董为浩, 高大冬. 一种优化的贝叶斯估计多传感器数据融合方法[J]. 传感技术学报, 2014, 27(5): 643-648. |
| [16] |
MANYIKA J, DURRANT-WHYTE H. Data fusion and sensor management:a decentralized information-theoretic approach[J]. Ellis Howard Limited, 1994(1): 22-26. |
| [17] |
KUMAR M, GARG D. Three-dimensional occupancy grid with the use of vision and proximity sensors in a robotic workcell[M]. CA: Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, 2004.
|
| [18] |
KUMAR M, GARG D. Intelligent multi sensor fusion techniques in flexible manufacturing workcells[J]. Proceedings of American Control Conference, 2004(2): 5375-5380. |
 2018, Vol. 32
2018, Vol. 32

