| 基于干扰观测器的欠驱动手指滑模控制 |
欠驱动多指手作为机器人通用化的末端执行器, 其控制输入小于控制输出, 以整体系统简洁高效、体积小、质量轻等优点, 得到了迅速的迭代发展, 已经广泛存在于制造业、医疗器械、机器人、航空航天等工业领域。相较于全驱动多指手更符合当下对机器人产业的需求。
欠驱动多指手能够以耦合方式实现相对多样性的抓取任务, 其控制方法多样化。针对欠驱动多指手的控制问题, 国内外学者进行了广泛的研究, 并提出了许多控制方案, 主要有比例积分微分(proportional integral derivative, PID)控制[1]、自适应控制[2]、鲁棒控制[3]、神经网络控制[4]、模糊控制[5]、迭代学习控制[6]、滑模变结构控制[7]、反馈线性化[8]等。Richa Sharma等[9]提出了分数阶模糊PID(fractional order fuzzy PID, FOFPID)控制器应用于双连杆平面刚性机械臂轨迹跟踪问题, 绝对误差积分和控制器输出绝对变化积分两个性能指标最小化权重, 使得机械臂在轨迹跟踪和抑制干扰等方面有着优良的性能。郭永凤[10]通过遗传算法在线优化和调整PID控制器参数, 控制液压机械手轨迹跟踪, 能抑制外界干扰, 提高手指末端定位精度。钱东海等[11]采用终端滑模控制方法, 使用多幂次趋近律提高滑模面收敛速度、降低滑模控制中的抖振现象, 提高机械手抓取控制的鲁棒性。唐庆顺等[12]采用非奇异终端滑模面设计控制律, 引入自适应方法估计未知不确定性, 大大削弱了抖振现象, 实现了机械手轨迹的高精度追踪。
欠驱动由于其控制变量个数小于系统自由度个数而难以精准控制, 将欠驱动多指手单指的二连杆模型简化为单指模型, 手指自身重力部分和未知扰动部分合并为干扰项, 探讨基于干扰观测器的欠驱动多指手末端手指轨迹跟踪控制问题。首先, 设计饱和函数趋近律的滑模控制器, 构造干扰观测器, 实时估计末端手指受到的外界干扰, 并在输入端进行相应的动态补偿, 改善末端手指的轨迹跟踪性能。与传统滑模控制器相比, 本文设计的基于干扰观测器的滑模控制器, 提高了轨迹跟踪精度, 削弱了抖振现象, 增强了控制器的鲁棒性。
1 欠驱动单指动力学模型欠驱动多指手手指为二连杆结构, 其动力学模型如图 1所示, 图中m1, m2分别表示两个连杆的质量;θ1, θ2分别表示连杆与水平方向夹角和连杆之间的夹角;l1, l2分别表示二连杆的长度;lc表示连杆质心到坐标原点的距离;τ表示作用在连杆上的控制力矩。l1杆与电机为齿轮传动, 传动点固定在机体轴上, 电机与l2杆为链条传动, 传动链条的一端也固定在机体轴上, 故l1杆与l2杆运动转角和转动扭矩存在一定比例关系, 比例由两者的传动比确定。由于两杆之间质量存在差距, 且l1比l2长, 手指整体的质心可以近似地认为在l1杆中心稍微靠上的位置。此外该手指二连杆结构的连接处均是刚性连接, 则本欠驱动多指手手指在实际控制方案可以简化为单指控制。
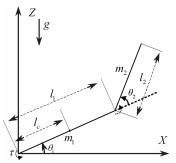 |
| 图 1 欠驱动单指模型 |
利用Newton-Euler方程可得到二连杆的动力学方程[13-14]为:
| $ \boldsymbol{M}(\boldsymbol{\theta}) \mathit{\boldsymbol{\ddot \theta }}+\boldsymbol{V}(\boldsymbol{\theta}, \mathit{\boldsymbol{\dot \theta }}) \mathit{\boldsymbol{\dot \theta }}+\boldsymbol{G}(\boldsymbol{\theta})+\boldsymbol{\tau}_{{\bf{d}}}=\boldsymbol{\tau}, $ | (1) |
其中,θ为手指关节转角位置;
考虑手指建模误差, 有:
| $ \left\{\begin{array}{l} \boldsymbol{M}(\boldsymbol{\theta})=\boldsymbol{M}_0(\boldsymbol{\theta})+{\bf{\Delta }} \boldsymbol{M}(\boldsymbol{\theta}) \\ \boldsymbol{V}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}})=\boldsymbol{V}_0(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}})+{\bf{\Delta }} \boldsymbol{V}(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}}) \\ \boldsymbol{G}(\boldsymbol{\theta})=\boldsymbol{G}_0(\boldsymbol{\theta})+{\bf{\Delta }} \boldsymbol{G}(\boldsymbol{\theta}) \end{array}\right., $ | (2) |
式中M0(θ)、V0(θ,
实际动力学方程为:
| $ \boldsymbol{M}_0(\boldsymbol{\theta}) \ddot{\boldsymbol{\theta}}+\boldsymbol{V}_0(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}}) \dot{\boldsymbol{\theta}}+\boldsymbol{G}_0(\boldsymbol{\theta})=\boldsymbol{\tau}-\boldsymbol{d}, $ | (3) |
其中,d=ΔM(θ)
整理公式(3), 得:
| $ \ddot{\boldsymbol{\theta}}=-\frac{\boldsymbol{V}_0(\boldsymbol{\theta}, \dot{\boldsymbol{\theta}})}{\boldsymbol{M}_0(\boldsymbol{\theta})} \dot{\boldsymbol{\theta}}+\frac{1}{\boldsymbol{M}_0(\boldsymbol{\theta})} \boldsymbol{\tau}-\frac{\boldsymbol{d}}{\boldsymbol{M}_0(\boldsymbol{\theta})}, $ | (4) |
简化后的单手指模型, 参数整理为:
| $ M_0(\theta)=I_1=\frac{4}{3} m_1 l_1^2 ; V_0(\theta, \dot{\theta})=\nu ; G_0(\theta)=\left(m_1+m_2\right) g l_{\mathrm{tc}} \cos \left(\theta_1\right) ; d={\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}} I \ddot{\theta}_1+{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}} \nu \dot{\theta}_1+{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}} G(\theta)+\tau_{\mathrm{d}} ; $ |
式中I1表示l1杆的转动惯量;ν表示手指运动中的黏性摩擦力;ltc表示手指整体质心距转动原点的距离;τd表示手指运动过程中受到的未知非线性干扰。由于手指均为刚体, 且对外作用力较小, 这里假设手指与外界作用时的弹性摩擦力忽略不计;手指运动的黏性摩擦力不易求得, 这里选用库伦摩擦力代替, τfriction=ccsgn(
| $ \ddot{\theta}=-b \dot{\theta}+a \tau-f \text {, } $ | (5) |
其中:
控制方案如图 2所示, 外界干扰主要来源于机械零部件的设计和装配误差、建模不确定部分和系统外部干扰。这部分外界干扰与欠驱动单指的重力共同构成总干扰, 通过设计干扰观测器对总干扰大小进行估计, 并在控制器端进行补偿, 由滑模控制器进行控制, 以提高控制轨迹跟踪精度。
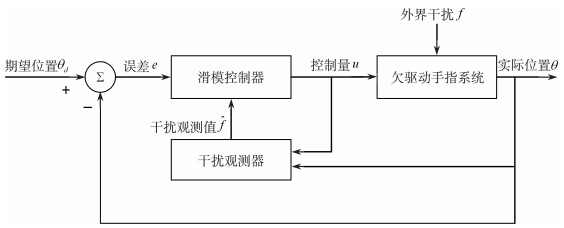 |
| 图 2 欠驱动单指末端轨迹跟踪控制方案 |
2.1 传统滑模控制
为了精准的控制手指末端轨迹, 现做如下假设:
假设一: 期望角度θd及其n阶导数存在且有界。
假设二: 不明确干扰项d有界, 其上界在系统的承受范围之内, 即|d|≤dmax, 则f有界。
定义跟踪误差为e=θd-θ, 其中θd∈R, 其导数为:
| $ s=c e+\dot{e}, $ | (6) |
其中, c>0。
设计传统滑模控制器为:
| $ u=\frac{1}{a}\left[\ddot{\theta}_{\mathrm{d}}+b \dot{\theta}+c \dot{e}+k_{\mathrm{f}} \operatorname{sgn}(s)\right], $ | (7) |
其中,kf为切换增益, 且kf>f。
定义Lyapunov函数为:
| $ V_{\mathrm{t}}=\frac{1}{2} s^2, $ | (8) |
对Vt求导, 可得:
| $ \dot{V}_{\mathrm{t}}=s \dot{s}=s\left(\ddot{\theta}_{\mathrm{d}}+b \dot{\theta}-a u+f+c \dot{e}\right)=s\left(f-k_{\mathrm{f}} \operatorname{sgn}(s)\right)=\left(f-k_{\mathrm{f}}\right)|s| \leqslant 0 \text { 。} $ | (9) |
根据Lyapunov稳定性定理可知传统滑模控制器可以在有限时间内趋于稳定。
2.2 基于干扰观测器的滑模控制器设计为提高控制性能, 对外界干扰进行实时观测, 设计干扰观测器为:
| $ \left[\begin{array}{c} {\dot {\hat {f}}} \\ {\dot {\hat {\omega}}} \end{array}\right]=\left[\begin{array}{cc} 0 & 0 \\ 1 & -b \end{array}\right]\left[\begin{array}{l} \hat{f} \\ \dot{\theta} \end{array}\right]+\left[\begin{array}{l} 0 \\ -a \end{array}\right] u+\left[\begin{array}{l} K_1 \\ K_2 \end{array}\right](\hat{\omega}-\dot{\theta}), $ | (10) |
其中,
设计滑模控制器为:
| $ u=\frac{1}{a}\left[\ddot{\theta}_{\mathrm{d}}+b\dot{\theta}+c \dot{\theta}+\hat{f}+\eta \operatorname{sgn}(s)\right], $ | (11) |
式中|f-
通过Lyapunov稳定性定理对上述滑模控制器的稳定性进行证明。定义如下Lyapunov函数:
| $ \left\{\begin{array}{l} V_1=\frac{1}{2} s^2 \\ V_2=\frac{1}{2 K_1} \tilde{f}^2+\frac{1}{2} \tilde{\omega}^2 \end{array}, \right. $ | (12) |
其中,
| $ \dot{V}_1=s\left(\ddot{\theta}_{\mathrm{d}}+b \dot{\theta}-a u+f+c \dot{e}\right)=s(f-\hat{f}-\eta\operatorname{sgn}(s))=\tilde{f} s-\eta|s| \leqslant 0, $ | (13) |
| $ \dot{V}_2=\frac{1}{K_1} \tilde{f}(\dot{f}-\dot{\hat{f}})+\tilde{\omega}(\ddot{\theta}-\dot{{\hat {\omega}}})=\frac{1}{K_1} \tilde{f} \dot{f}-K_2 \tilde{\omega}^2, $ | (14) |
假设干扰f为慢时变信号, 即
| $ \frac{1}{K_1} \dot{f}=0, $ | (15) |
则
| $ \dot{V}_2=-K_2 \tilde{\omega}^2 \leqslant 0, $ | (16) |
当
取闭环系统的Lyapunov函数为:
| $ V=V_1+V_{2}。$ | (17) |
由上述可得:
上述控制器使用符号函数sgn(s), 会出现抖振现象。为削弱抖振现象, 本文用饱和函数sat(s)代替符号函数sgn(s)。饱和函数表达式为sat(s)=
为验证所设计控制方法的控制性能, 以图 1欠驱动单指为例, 通过MATLAB进行仿真验证, 并与传统滑模控制器进行性能对比。
4.1 仿真参数与初始条件设置仿真时间为10 s。欠驱动单指参数为: l1=0.1 m, m1=0.06 kg, l2=0.05 m, m2=0.036 kg, g=9.81 m/s2, ltc=0.07 m。粘性摩擦系数ν不易测量由库仑摩擦力代替, 假定动摩擦系数cc=0.3。选取初始状态为水平状态, 即θ1=0, 期望转角位置为θ1=
图 3描述了所设计控制器与传统滑模控制的轨迹跟踪对比曲线, 可以看出本文提出的控制方法能够更快的收敛于期望值, 且跟踪轨迹稳定。
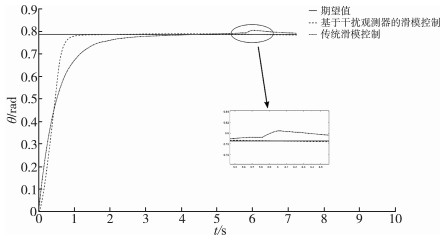 |
| 图 3 轨迹跟踪对比图 |
图 4描述了两种滑模控制器的控制量曲线, 传统滑模控制的控制量抖振现象明显;基于干扰观测器的滑模控制通过引入干扰观测器和使用饱和函数sat(s)代替符号函数sgn(s)后, 极大抑制了抖振现象的发生。
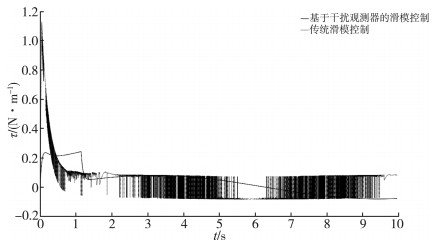 |
| 图 4 控制输入对比图 |
图 5描述了实际干扰与估计干扰的实时关系, 可以看出干扰观测器可以在极短的时间估计出欠驱动单指运动过程中估计外部干扰, 并作出反馈, 上述仿真结果验证了本文控制方法就有较强的稳定性能和鲁棒性能。
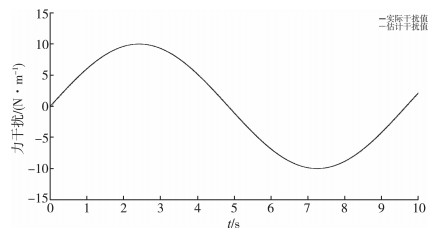 |
| 图 5 实际干扰与估计干扰 |
4.3 干扰观测器的方波响应与误差分析
为测试基于干扰观测器的滑模控制器的干扰估计能力, 将外界干扰设置为如图 6所示的方波信号, 直线表示外界实际干扰值, 虚线表示干扰的估计值, 可以看出干扰估计值小幅超调后快速收敛于实际值, 实际值与估计值的误差很小, 表明干扰观测器有能力实时估计出外界干扰。图 7为外界干扰是3种频率的慢时变正弦信号时的干扰估计误差值, 可以看出误差值稳定后也是正弦信号, 误差的频率由干扰的频率决定, 误差的估计精度也取决于干扰频率。干扰信号频率越高, 估计误差的精度越低, 反之, 干扰信号频率越低, 估计误差的精度越高。仿真结果验证了本文控制方法的精准性。
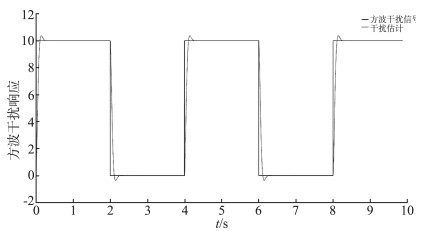 |
| 图 6 干扰观测器的方波信号响应 |
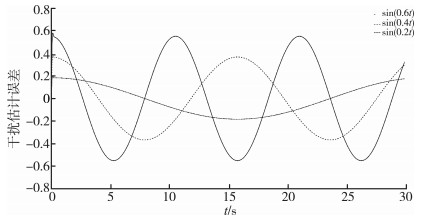 |
| 图 7 不同频率干扰的估计误差 |
5 结论
为了提高控制系统的精准控制性能和鲁棒性能, 建立了欠驱动指模型, 提出了一种基于干扰观测器的滑模控制器。通过引入干扰观测器和饱和函数滑模趋近律, 分别用于实时估计外界干扰值的大小和抑制抖振现象, 干扰估计值作用于控制输入端, 在控制端给出相应补偿。由仿真实验得出, 在存在外界干扰的情况下, 设计的基于干扰观测器的滑模控制器有着良好的控制性能和鲁棒性能, 可以应用于欠驱动多指手的抓取控制。
| [1] |
ALVAREZ RAMIREZ J, CERVANTES I, KELLY R. PID regulation of robot manipulators: stability and performance[J]. Systems & Control Letters, 2000, 41: 73-83. |
| [2] |
王泰华, 田辈辈, 高煜欣. 基于改进自适应算法的机械臂位置/力控制研究[J]. 制造业自动化, 2020, 42(3): 85-89. |
| [3] |
夏鹏程, 罗建军, 王明明. 空间双臂机器人抓捕翻滚目标后的鲁棒稳定控制[J]. 力学学报, 2021, 53(4): 1138-1155. |
| [4] |
郑华辉, 方宗德. 基于自适应神经网络控制的机械臂运动轨迹跟踪误差研究[J]. 机械设计与制造, 2019, 340(6): 139-141. |
| [5] |
LIU Z, WANG F, ZHAND Y. Adaptive visual tracking control for manipulator with actuator fuzzy dead-zone constraint and unmodeled dynamic[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 45: 1301-1312. DOI:10.1109/TSMC.2015.2420037 |
| [6] |
WANG D, HA M, QIAO J. Data-Driven iterative adaptive critic control towards an urban wastewater treatment plant[J]. IEEE Transactions on Industrial Electronics, 2020(99): 1-1. |
| [7] |
席雷平, 何辉, 黄海瑞. 机械臂轨迹跟踪滑模控制中的抖振抑制法研究[J]. 计算机仿真, 2012, 29(5): 188-191. |
| [8] |
赵海滨, 刘冲, 陆志国, 等. 基于Matlab/Simulink的欠驱动机械臂仿真实验[J]. 实验技术与管理, 2018, 35(6): 135-138. |
| [9] |
SHARMA R, RANA K P S, KUMAR V. Performance analysis of fractional order fuzzy PID controllers applied to a robotic manipulator[J]. Expert Systems with Applications, 2014, 41(9): 4274-4289. |
| [10] |
郭永凤. 基于改进PID控制的移动液压机械手轨迹追踪研究[J]. 舰船电子工程, 2019, 39(10): 79-82. |
| [11] |
钱东海, 黄友昕, 董小康, 等. 基于快速终端滑模算法的机械手跟踪控制研究[J]. 中国机械工程, 2017, 28(18): 2237-2241. |
| [12] |
唐庆顺, 金璐, 李国栋, 等. 基于自适应终端滑模控制器的机械手跟踪控制[J]. 山东大学学报(工学版), 2016, 46(5): 45-53. |
| [13] |
BRUNO SICILIANO, KIMON P, VALAVANIS. Controlproblems in robotics and automation[M]. Berlin, Heidelberg: Springer, 2005.
|
| [14] |
刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418. |
| [15] |
林壮, 段广仁, 宋申民. 水平欠驱动机械臂的反步自适应滑模控制[J]. 机器人, 2009, 31(2): 131-136. |
 2023, Vol. 37
2023, Vol. 37


