| 一维高阶非线性晶格链中的负微分热阻 |
最近二十年, 低维体系中的热输运研究一直受到人们的广泛关注。特别是随着纳米材料和纳米制备技术的快速发展, 许多低维材料展现出良好的热性能, 但是关于低维热输运的理论尚未完全建立。研究表明, 在低维体系中, 由于非线性作用的影响, 一些体系中存在负微分热阻效应[1-4]。负微分热阻表现为: 当体系两端存在温差时, 通过体系的稳态热流会随着温差的增加而减小。相反, 如果通过体系的稳态热流随着温差的增加而增大, 则体系具有正微分热阻。负微分热阻效应是设计热晶体管[5]、热逻辑器件[6]的必要条件, 这些热器件可以实现对微纳热流的控制。Yang等[1]提出了具有质量梯度的一维FPU-β晶格模型, 并计算研究了体系中的热传导性质, 结果显示, 当轻粒子端温度高, 重粒子端温度低时, 体系中出现了负微分热阻效应。一维质量梯度FPU-β模型实际上只考虑了粒子间的四次非线性相互作用。我们注意到, 高阶非线性相互作用往往会令晶格体系表现出更丰富的动力学行为, 如孤立波、呼吸子[7-8], 这些非线性激发在一定程度上会对热载流子(声子)产生作用, 从而影响其热输运行为。
本文利用非平衡分子动力学模拟的方法研究了当粒子间具有六次非线性作用时, 一维质量梯度晶格中的热传导及负微分热阻性质。
1 模型与方法考虑具有质量梯度的一维非线性晶格链(图 1), 体系的哈密顿量可以表示为:
 |
| 图 1 一维质量梯度晶格链示意图 |
| $ \begin{array}{l} \ \ \ \ \ \ \ H=\sum\limits_{i}\left(\frac{p_{i}^{2}}{2 M_{i}}+\frac{1}{2}\left(x_{i+1}-x_{i}\right)^{2}+\right. \\ \left.U\left(x_{i}\right)\right)。\end{array} $ | (1) |
其中pi、xi和Mi分别表示第i个粒子的动量、位移和质量;并设定粒子质量取:
| $ M_{i}=M_{\max }-(i-1)\left(M_{\max }-M_{\min }\right) /(N-1)。$ | (2) |
则质量最重的粒子将位于体系的端点处(图 1的左端), 其质量为Mmax;质量最轻粒子将位于体系的另一个端点处(图 1的右端), 质量为Mmin;选取:
| $ \begin{array}{l} \ \ \ \ U\left(x_{i+1}, x_{i}\right)=\frac{k_{4}}{4}\left(x_{i+1}-x_{i}\right)^{4}+\frac{k_{6}}{6} \\ \left(x_{i+1}-x_{i}\right)^{6}。\end{array} $ | (3) |
表示粒子之间的非线性相互作用, k4、k6分别表示四次非线性和六次非线性的强度, 当k6=0, k4≠0时, 就回到一维质量梯度FPU-β晶格链。为了在体系中产生热流, 采用两个温度分别为TL和TH的Nosé-Hoover型热浴, 并分别耦合于体系两端的粒子上;TL和TH分别表示低温和高温热浴的温度。设定系统具有固定边界条件, 即x0=xN+1=0。这样, 链中粒子的运动方程可表示为:
| $ \begin{array}{*{20}{l}} {{{\dot x}_i} = {p_i}/{M_i},}\\ {{M_i}{{\ddot x}_i} = \left\{ {\begin{array}{*{20}{l}} { - {\zeta _L}{{\dot x}_1} - \frac{{\partial {H_1}}}{{\partial {x_1}}},\quad i = 1}\\ { - \frac{{\partial {H_i}}}{{\partial {x_i}}},\quad 2 \le i \le N - 1}\\ { - {\zeta _H}{{\dot x}_N} - \frac{{\partial {H_N}}}{{\partial {x_N}}},i = N} \end{array}} \right.}。\end{array} $ | (4) |
热浴所满足的运动方程分别为:
| $ \dot{\zeta}_{L}=\frac{M_{1} \dot{x}_{1}^{2}}{T_{L}}-1 , $ | (5) |
| $ \dot{\zeta}_{H}=\frac{M_{N} \dot{x}_{N}^{2}}{T_{H}}-1。$ | (6) |
根据维里定理, 单个粒子的动能温度定义为:
| $ T(i)= < p_{i}^{2} / M_{i} >, $ | (7) |
系统达到非平衡稳定后, 流过整个体系的热流定义为:
| $ J=j(i)=<\frac{1}{2} a\left(\dot{x}_{i+1}+\dot{x}_{i}\right)\left(\dot{x}_{i}-\dot{x}_{i+1}\right)>。$ | (8) |
其中<…>代表系综平均, 参数a是晶格常数, 在本文中取a=1。在计算过程中, 用时间平均代替系综平均, 微分方程组通过四阶龙格库塔法则进行求解, 如无特别说明, 则Mmax=10、Mmix=1、TH=0.4、n=100。
2 计算模拟与结果首先, 固定高温热浴的温度, 然后分别将高温热浴耦合到重粒子(Mmax)和轻粒子(Mmix)端, 通过调节低温热浴的温度(TL), 计算研究了当体系达到非平衡稳态时, 流过体系的平均热流。结果显示, 在只有四次非线性势(k6=0)或只有六次非线性势(k4=0)的情况下, 当高温热浴耦合到重粒子端时, 随着低温热浴温度的减小(此时体系两端的温差逐渐增大, 平均温度逐渐减小), 流过体系的平均热流都是逐渐增大的, 都表现为正微分热阻(图 2)。然而, 当把高温热浴耦合到轻粒子端时, 在只有四次非线性势(k6=0)或只有六次非线性势(k4=0)的作用下, 随着低温热浴温度的减小, 流过体系的平均热流一开始会随着温差的增大而增大, 表现为正微分热阻;当低温热浴温度低于某一温度时, 则会出现平均热流随着温差的增大而减小的情况, 即在此区域表现为负微分热阻(图 3), 这表明六次非线性势同样可以令体系中出现负微分热阻效应。此外, 从图 3中还可以看出, 当k4或k6很弱时(0.1), 体系中的非线性效应可以近似忽略不计, 体系退化为一维质量梯度简谐晶格链, 体系中没有负微分热阻效应。
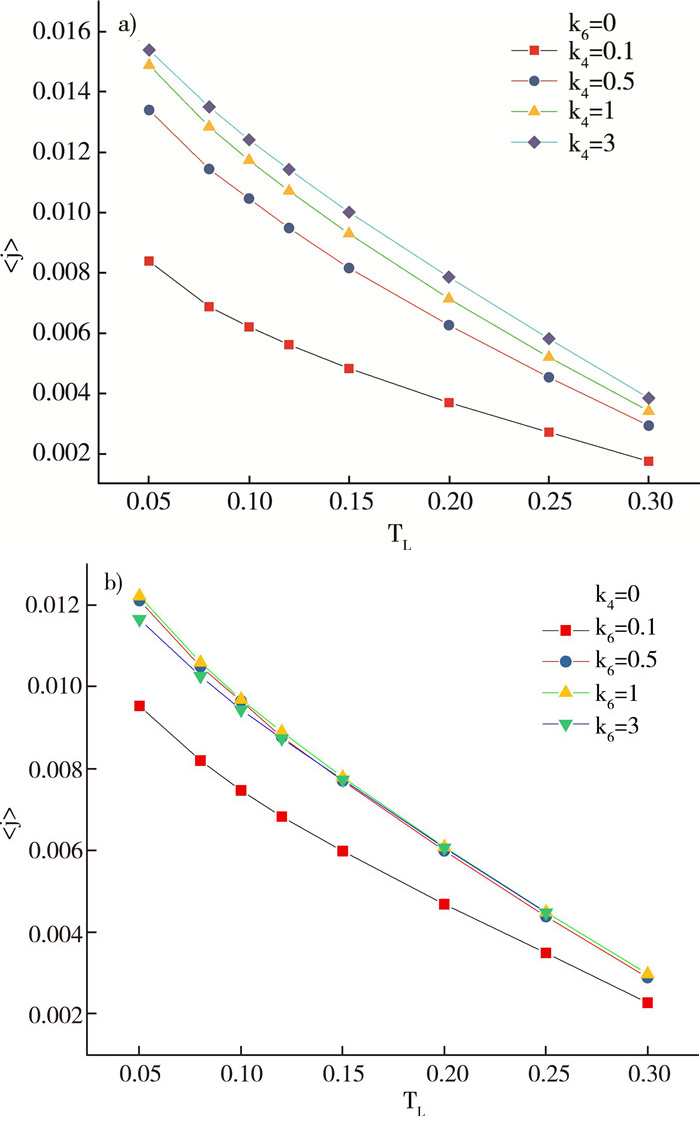 |
| 注: a)只有四次非线性势作用;b)只有六次非线性势作用 图 2 高温热浴TH同重粒子端Mmax耦合时, 体系中的平均热流随低温热浴变化的关系 |
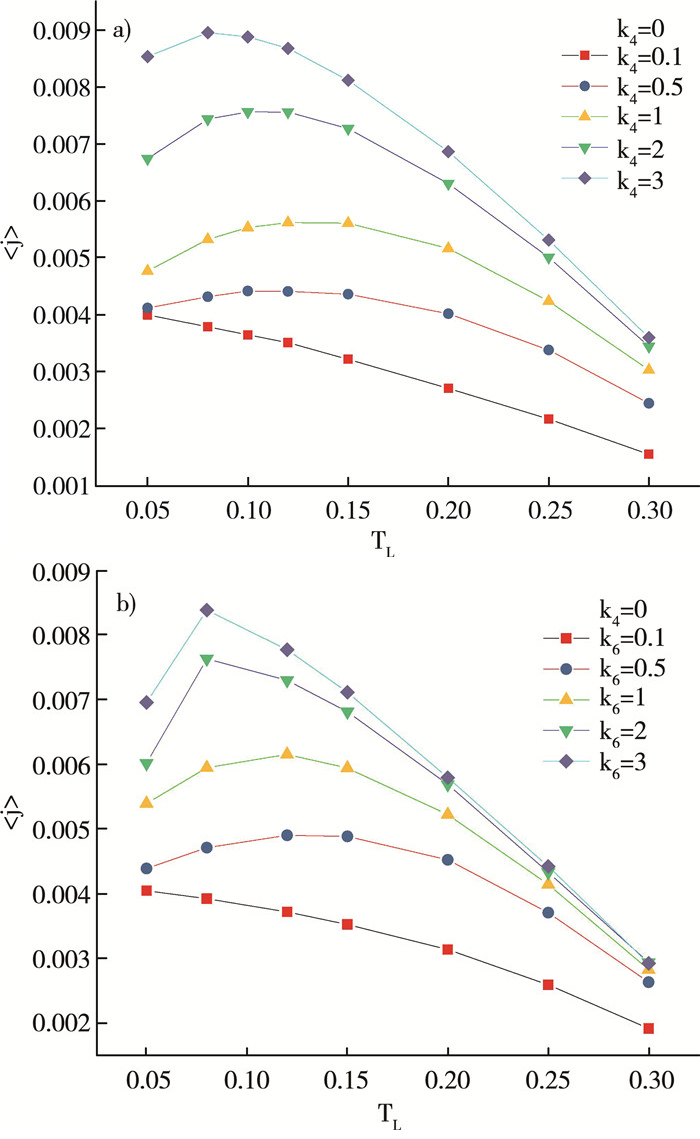 |
| 注: a)只有四次非线性势作用;b)只有六次非线性势作用 图 3 高温热浴TH同轻粒子端Mmin耦合时, 体系中的平均热流随低温热浴变化的关系 |
根据上述结果, 当高温热浴耦合到重粒子端时, 此时体系中只有正微分热阻, 我们计算研究了体系中的平均热流随着四次非线性势强度或六次非线性势强度的变化情况。图 4 a)表明, 随着非线性势强度(k4或k6)的增强, 体系中的平均热流都会趋于饱和。但是, 当高温热浴耦合到轻粒子端时, 体系中会产生负微分热阻效应。此时, 在正微分热阻区域, 体系中的平均热流依然会随着四次非线性势或六次非线性势的增强趋于饱和;不过在负微分热阻区域, 体系中的平均热流会随着四次非线性势或六次非线性势的增强而增大,不会出现饱和的状态(图 4 b))。
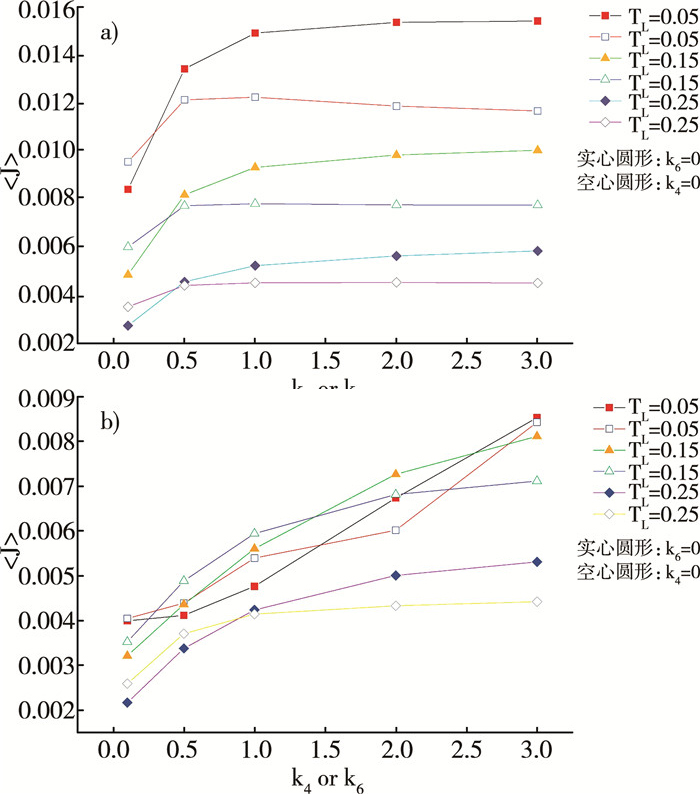 |
| 注: a)高温热浴同重粒子端耦合;b)高温热浴同轻粒子端耦合 图 4 平均热流随四次非线性势强度或六次非线性势强度的变化关系 |
我们还计算研究了在体系取不同的尺寸时, 格点间的六次非线性势对负微分热阻的影响程度。此时高温热浴耦合在轻粒子端, 为了方便比较, 同时给出了相同情况下四次非线性势对负微分热阻的影响情况。从图 5 a) 可以看出, 体系的尺寸比较小时, 具有六次非线性势的晶格链中的负微分热阻区域跟相同情况下具有四次非线性势的晶格链中的负微分热阻区域几乎一样, 只是具有六次势的体系中容许通过的平均热流较大;但当体系的尺寸较大时, 从图 5 b)至d)中可以看出, 具有六次势的晶格链中的负微分热阻区域明显小于只具有四次势的晶格链中的负微分热阻区域。也就是, 当体系的尺寸达到一定值后, 晶格间的六次非线性相互作用会削弱负微分热阻效应。
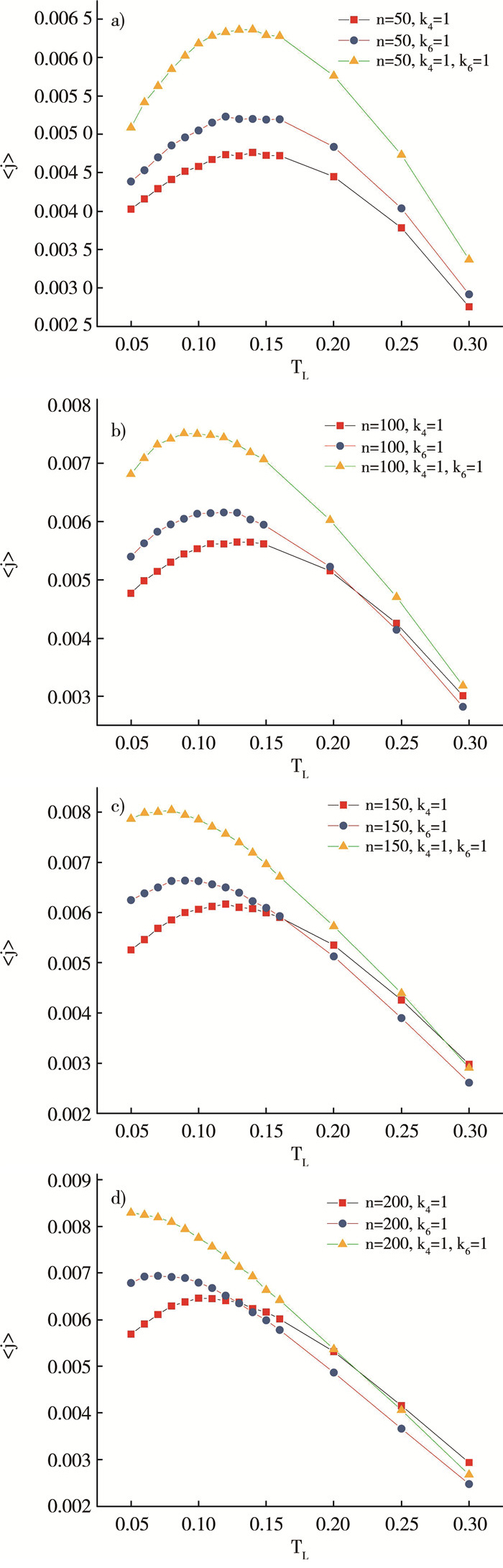 |
| 图 5 不同尺寸下的平均热流随低温热浴TL的变化关系 |
为了进一步说明负微分热阻与系统尺寸之间的关系, 模拟计算了在只考虑四次势和六次势时, 不同尺寸下体系中的平均热流随低温热浴的变化曲线。从图 6 a)中可以看出, 在只考虑四次势时, 负微分热阻区域会随着体系尺寸的增加逐渐减少, 最终负微分热阻趋于消失。其中的黄色竖线表示体系在n=200时, 负微分热阻出现在TL < 0.11的区域内, 此结果跟Yang等的研究结果是一致的[1];在只考虑六次势时, 同样出现负微分热阻区域随着体系尺寸的增加逐渐减少并最终消失的情况, 但是在六次势的作用下负微分热阻区域减少得更快。
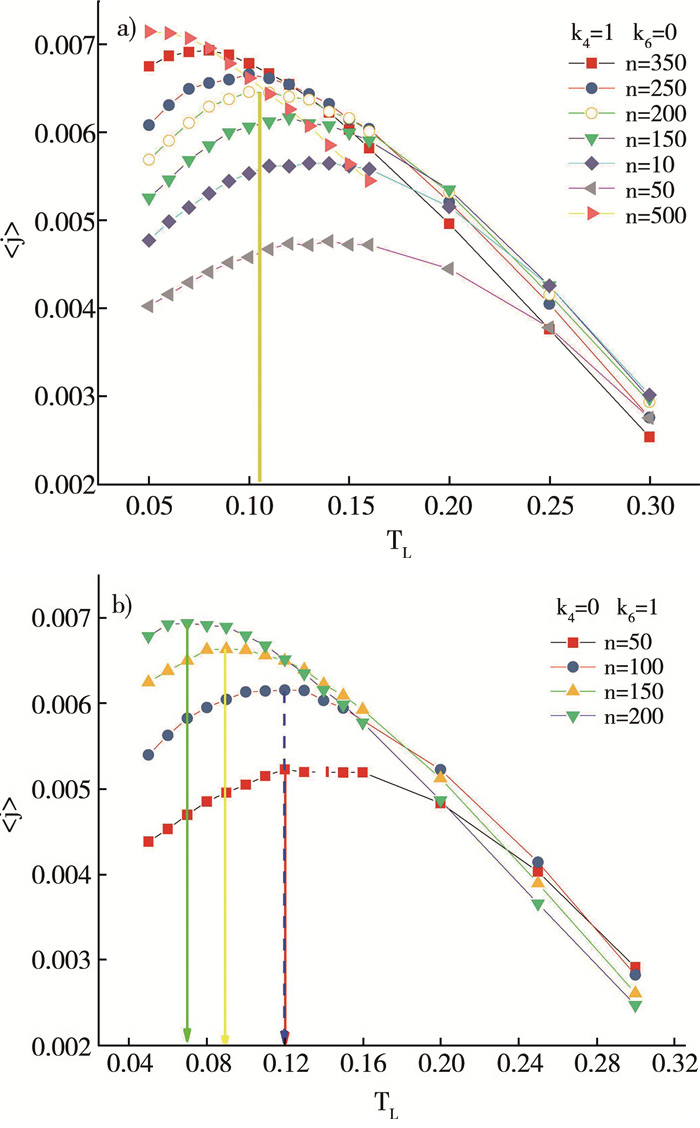 |
| 注: a)只有四次非线性势作用;b)只有六次非线性势作用 图 6 负微分热阻区域随系统尺寸的变化关系 |
3 结论
综上所述, 本文使用非平衡分子动力学模拟的方法系统地研究了在考虑晶格间的六次非线性相互作用时, 一维质量梯度晶格体系中的负微分热阻效应。从结果来看, 在六次势的作用下, 体系中的负微分热阻与只考虑四次势作用时有所不同。此结果更接近于真实体系的情况, 对进一步设计微纳热控制器件有一定理论指导意义。
| [1] |
YANG N, LI N B, WANG L, et al. Thermal rectification and negative differential thermal resistance in lattices with mass gradient[J]. Phys.Rev.B, 2007, 76(2): 020301. DOI:10.1103/PhysRevB.76.020301 |
| [2] |
ROBERTS N A, WALKER D G. A review of thermal rectification observations and models in solid materials[J]. International Journal of Thermal Sciences, 2011, 50(5): 648-662. DOI:10.1016/j.ijthermalsci.2010.12.004 |
| [3] |
ZHANG X, MA K, ZHANG J, et al. Effect of lattice period on thermal current of Frenkel-Kontorova lattices[J]. The European Physical Journal B, 2018, 91(12): 317. DOI:10.1140/epjb/e2018-90523-8 |
| [4] |
CHEN X K, XIE Z X, ZHOU W X, et al. Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction[J]. Carbon, 2016, 100: 492-500. DOI:10.1016/j.carbon.2016.01.045 |
| [5] |
LI B, WANG L, CASATI G. Negative differential thermal resistance and thermal transistor[J]. Appl.Phys.Lett, 2006, 88(14): 143501. DOI:10.1063/1.2191730 |
| [6] |
WANG L, LI B. Thermal logic gates: computation with phonons[J]. Phys.Rev.Lett, 2007, 99(17): 177208. DOI:10.1103/PhysRevLett.99.177208 |
| [7] |
KEVREKIDIS P G, MALOMED B A, SAXENA A, et al. Higher-order lattice diffraction: solitons in the discrete NLS equation with next-nearest-neighbor interactions[J]. Physica D: Nonlinear Phenomena, 2003, 183(1-2): 87-101. DOI:10.1016/S0167-2789(03)00178-7 |
| [8] |
GUO R, HAO H Q. Breathers and multi-soliton solutions for the higher-order generalized nonlinear Schrdinger equation[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(9): 2426-2435. DOI:10.1016/j.cnsns.2013.01.019 |
 2021, Vol. 35
2021, Vol. 35


