| 智能反射面辅助的多用户边缘计算卸载研究 |
随着用户数量和设备类型的大幅增加, 通信技术向高带宽, 高可靠性的方向不断发展[1]。移动边缘计算(mobile edge computing, MEC)作为一种物联网开发通信和计算基础设施的新范式, 通过将计算能力下放到靠近用户端的边缘服务器, 以克服存在通信网络中高延迟和低带宽的缺点。在未来通信网络的设想中, 网络不仅要满足高带宽与高可靠性的需求, 还需要满足绿色通信的未来发展, 因此智能反射面(intelligent reflecting surface, IRS)技术走进人们的视野[2]。
移动边缘计算相较于传统的网络架构具有很多优势, 计算能力的下放为用户带来更低时延的体验, 减少数据传输过程中的能量消耗, 避免核心网络的数据拥堵等, 这些优势使得移动边缘计算技术成为5G和6G中一项关键技术。在无线信道中, 智能反射面通过调整反射波束的形成, 在信号接收处, 多路信号的叠加提高基站接收信号的功率, 从而提升系统在传输信道情况差的条件下, 系统的传输性能。智能反射面的构成简单, 安装灵活多变, 包括无源反射单元以及控制器组成, 无需任何射频链即可实现无源波束形成[3], 智能反射面控制器能够进行反射信号幅度的控制、相位的改变和频率的变换。
在移动边缘计算系统设计中, 计算卸载策略起着至关重要的作用[4]。目前, 在文献[5]中提出二进制卸载策略来是否进行决定本地计算, 还是执行计算卸载将任务卸载到边缘节点处理任务。在文献[6]中提出部分卸载处理方案, 将计算任务分成两部分, 分别在本地与边缘服务器处理。在这些研究中, 通过计算资源分配来达到低时延的效果, 缺少对无线信道控制的关注。在文献[7]中, 在无线信道对比智能反射面与传统中继, 证明了智能反射面辅助的无线系统具有大的能量增益。因此, 将智能反射面技术引入到移动边缘计算系统中, 提高计算卸载过程中通信效率很有必要。
在移动边缘计算模型中引入智能反射面, 提高计算卸载过程中的通信效率; 考虑多用户随机接入的计算卸载场景, 更加符合海量接入的需求; 采用交替优化算法, 分析了用户请求时延最小化的问题, 解决了计算资源分配和智能反射面优化问题。
1 系统模型 1.1 通信模型如图 1所示, 构建智能反射辅助的多用户MEC的模型, 该系统包括一个M天线并搭载边缘服务器的基站, N个无源反射单元和A个有源反射单元的智能反射面, 辅助K个单天线用户处理计算任务。无源反射单元具有最佳单位振幅, 通过反射单元的硬件电路控制设计对入射信号相位的独立控制, 相比无源反射单元, 有源反射单元具备调整的相位和振幅作用。K个单天线用户按每个用户请求顺序来进行排队, 通过TDMA方式卸载[8]。为方便记录, 分别将用户、智能反射面无源和有源反射单元记录为k∈K= { 1, 2, 3, …, K }, n∈N={1, 2, 3, …, N}和a∈A= {1, 2, 3, …, A}。
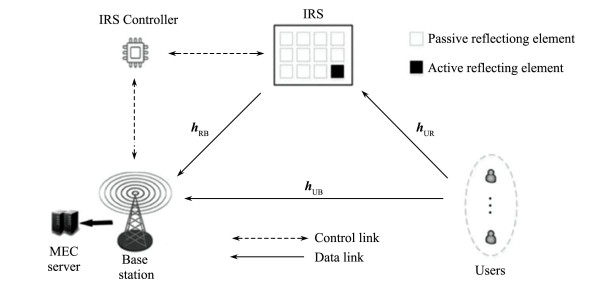 |
| 图 1 上行智能反射面辅助的移动边缘计算网络 |
假设用户, 智能反射面和基站的信道采用块衰落信道模型, 用户请求时间内的信道系数保持不变。由于基站和边缘服务器之间通过有线光缆进行连接, 任务传输时延忽略不计。由于存在高路径损耗, 只记录经过反射面一次反射的信号。用
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left\{ {{\alpha _k} = \left| {{\alpha _k}} \right|{{\rm{e}}^{{\rm{j}}{\theta _k}}}} \right\}, \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = \left\{ {{\beta _k} = \left| {{\beta _k}} \right|{{\rm{e}}^{{\rm{j}}{\vartheta _k}}}} \right\}, $ | (1) |
在上行链路传输数据期间, 用户k的发送信号为sk, 智能反射面的接收信号表示为
| $ {P_a}(\beta ) = {\mathop{\rm tr}\nolimits} \left[ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {\sqrt {{P_k}} {h_{UR}}h_{{\rm{UR}}}^H + \delta _k^2{I_{(N + A)}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^H}} \right], $ | (2) |
基站接收信号如下表示:
| $ {y_k} = \sqrt {{P_k}} \left( {{\mathit{\boldsymbol{h}}_{{\rm{UB}}}} + {\mathit{\boldsymbol{h}}_{{\rm{UR}}}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{\mathit{\boldsymbol{h}}_{{\rm{RB}}}}} \right){s_k} + {\mathit{\boldsymbol{h}}_{{\rm{UR}}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{n_{{\rm{UR}}}} + {n_{{\rm{BS}}}} = \sqrt {{P_k}} {\mathit{\boldsymbol{H}}_k}{s_k} + {n_k}, $ | (3) |
其中, Hk为等效信道的信道增益,
| $ {R_k} = B\ {\log _2}\left( {1 + {{{\mathop{\rm SINR}\nolimits} }_k}} \right) = B\ {\log _2}\left( {1 + \frac{{{P_k}{{\left| {\mathit{\boldsymbol{w}}_k^H{\mathit{\boldsymbol{H}}_k}} \right|}^2}}}{{\delta _k^2\mathit{\boldsymbol{w}}_k^HI{w_k}}}} \right)。$ | (4) |
由于本地计算资源受限, 需将本地部分计算任务上传到基站服务器处理。假设在用户计算任务卸载前, 用户产生计算任务后, 按照请求顺序来处理用户计算任务。假设用户产生的计算任务位数为Dk, 计算任务部分卸载或全部卸载到边缘服务器, 标记计算卸载量为dk, 用户的本地计算时间表示为
| $ T_k^l = \frac{{\left( {{D_k} - {d_k}} \right)\chi }}{{f_k^l}}, $ | (5) |
其中, χ为计算1 bit数据需要的CPU周期数, fkl为用户的计算频率, fkl≤fmaxl, fmaxl为本地计算的最高频率。计算卸载上行传输时间
| $ T_k^{{\rm{up}}} + T_k^e = \frac{{{d_k}}}{{{R_k}}} + \frac{{{d_k}\chi }}{{f_k^e}}。$ | (6) |
通过联合优化dk、wk、Θ, 以实现在用户发射功率、计算频率和边缘服务器计算频率约束下用户的计算平均时延最小化。首先定义用户处理任务的平均时延如下
| $ \bar T = \max \frac{1}{K}\sum\limits_{k = 1}^K {\left[ {T_k^l, \left( {T_k^{{\rm{up}}} + T_k^e} \right)} \right]} = \max \frac{1}{K}\sum\limits_{k = 1}^K {\left[ {\frac{{\left( {{D_k} - {d_k}} \right)\chi }}{{f_k^l}}, \left( {\frac{{{d_k}}}{{{R_k}}} + \frac{{{d_k}\chi }}{{f_k^e}}} \right)} \right]}。$ | (7) |
优化问题以及约束条件表述如下
| $ \begin{array}{l} P1:\mathop {\min }\limits_{{d_k}, {w_k}, \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \bar T, \\ {\rm{s}}{\rm{.t}}{\rm{. }}{C_1}:{d_k} \in \left[ {0, {D_k}} \right]{\rm{, }}\\ \;\;\;\;\;{C_2}:f_k^d \le f_{{\rm{max }}}^d, \\ \;\;\;\;\;{C_3}:\left| {{\varphi _k}} \right| = 1, \\ \;\;\;\;\;{C_4}:0 \le {\theta _k}, {\vartheta _k} \le 2\pi , \\ \;\;\;\;\;{C_5}:f_k^e \le {f_{{{\max }^e}}}, \\ \;\;\;\;\;{C_6}:{P_a}(\beta ) \le P_a^{\max }, \end{array} $ | (8) |
其中, C1是卸载数据量的约束, C2是本地用户计算频率约束, C3是智能反射面单元的反射信号幅度约束, C4是智能反射面单元和有源智能反射单元的反射信号幅度约束, C5是边缘服务器计算频率约束, C6是有源智能反射单元发射功率限制。
2.2 算法设计 2.2.1 卸载变量优化通过优化卸载变量使系统平均处理时延最小, 在固定智能反射面的对角相移矩阵和线性波束成形矢量的前提下, T求和项中前一项为dk的递减函数, 后一项为dk的递增函数。当本地计算时间与边缘计算时间相等时, T达到最小化。给出卸载变量最优解为
| $ d_k^* = \frac{{\chi {D_k}{R_k}f_k^e}}{{\chi {R_k}\left( {f_k^d + f_k^e} \right) + f_k^df_k^e}}。$ | (9) |
确定最优卸载变量dk后, 优化线性接收矢量wk和对角相移矩阵Θ 。在卸载变量优化中, 当本地计算时间与边缘计算时间相等时, T达到最小化。优化问题P1:
| $ \mathop {\max }\limits_{{w_k}, \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \left( {{{{\mathop{\rm SINR}\nolimits} }_k}} \right) = \mathop {\max }\limits_{{w_k}, \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \left( {\frac{{{P_k}{{\left| {\mathit{\boldsymbol{w}}_k^H{H_k}} \right|}^2}}}{{\delta _k^2\mathit{\boldsymbol{w}}_k^HI{w_k}}}} \right). $ | (10) |
当对角相移矩阵确定时, 根据最大比合并原则(maximum ratio combining, MRC)[9], 最佳w如下表示
| $ {w^*} = \sqrt {\frac{P}{{\delta _k^2}}} {\left( {{\mathit{\boldsymbol{I}}_M} + {\mathit{\boldsymbol{h}}_{{\rm{RB}}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^H}h_{RB}^H} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{h}}_{{\rm{UB}}}} + {\mathit{\boldsymbol{h}}_{{\rm{UR}}}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{\mathit{\boldsymbol{h}}_{{\rm{RB}}}}} \right)。$ | (11) |
优化有源智能反射面时, 采用与无源智能反射面相同的方法, 只考虑在基站处引入的高斯白噪声时, I矩阵成为IM单位矩阵, SINR表示如下
| $ \frac{{{P_k}{{\left| {\mathit{\boldsymbol{w}}_k^H\left( {{\mathit{\boldsymbol{h}}_{{\rm{UB}}}} + {\mathit{\boldsymbol{h}}_{{\rm{UR}}}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}{\mathit{\boldsymbol{h}}_{{\rm{RB}}}}} \right)} \right|}^2}}}{{\delta _k^2{{\left\| {{w_k}} \right\|}^2}}} \le \frac{{{P_k}}}{{\delta _k^2{{\left\| {{w_k}} \right\|}^2}}}{\left( {\left| {\mathit{\boldsymbol{w}}_k^H{\mathit{\boldsymbol{h}}_{{\rm{UB}}}}} \right| + \sum\limits_{n = 1}^N {\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}\mathit{\boldsymbol{w}}_k^H{\mathit{\boldsymbol{h}}_{{\rm{RB}}, n}}} \right|} } \right)^2}, $ | (12) |
其中, hUR, n是hUR的第n项, hRB, n是hRB的第n列。等号成立条件为
| $ {\theta ^*} = \arg \left\{ {\mathit{\boldsymbol{w}}_k^H{\mathit{\boldsymbol{h}}_{{\rm{UB}}}}} \right\} - \arg \left\{ {{\mathop{\rm diag}\nolimits} \left( {\mathit{\boldsymbol{w}}_k^H{\mathit{\boldsymbol{h}}_{{\rm{RB}}}}} \right){\mathit{\boldsymbol{h}}_{{\rm{UR}}}}} \right\}, $ | (13) |
智能反射单元的最优反射相位
| $ \begin{array}{l} {{\mathop{\rm SINR}\nolimits} _k} = \frac{{{P_k}}}{{\delta _k^2}} \cdot \frac{{{a_n}{{\left| {{\beta _k}} \right|}^2} + {b_n}\left| {{\beta _k}} \right| + {c_n}}}{{{u_n}{{\left| {{\beta _k}} \right|}^2} + {v_n}}}\\ {a_n} = {\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}} \right|^2}{\left| {{\mathit{\boldsymbol{w}}^H}{\mathit{\boldsymbol{h}}_{{\rm{RB}}, n}}} \right|^2}, {b_n} = 2\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}{\mathit{\boldsymbol{w}}^H}{\mathit{\boldsymbol{h}}_{{\rm{RB}}, n}}} \right|\sqrt {{c_n}} , {c_n} = {\left( {\left| {{\mathit{\boldsymbol{w}}^H}{\mathit{\boldsymbol{h}}_{{\rm{UB}}}}} \right| + \sum\limits_{i = 1, i \ne n}^N {\left| {{\beta _i}{\mathit{\boldsymbol{h}}_{{\rm{UR}}, i}}{\mathit{\boldsymbol{w}}^H}{\mathit{\boldsymbol{h}}_{{\rm{RB}}, i}}} \right|} } \right)^2}, \\ {u_n} = {\left| {{\mathit{\boldsymbol{w}}^H}{\mathit{\boldsymbol{h}}_{{\rm{RB}}, n}}} \right|^2}, {v_n} = {\left\| w \right\|^2} + \sum\limits_{i \in A, i \ne n} {{{\left| {{\beta _i}} \right|}^2}} {\left| {{w^H}{\mathit{\boldsymbol{h}}_{{\rm{RB}}, n}}} \right|^2}, {d_n} = {\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}} \right|^2}{v_n} - {c_n} \end{array} $ | (14) |
有源智能反射面振幅优化问题表述如下
| $ \begin{array}{*{20}{l}} {\mathop {\max }\limits_{_{\left| {{\beta _k}} \right|}} \frac{{{P_k}}}{{\delta _k^2}} \cdot \frac{{{a_n}{{\left| {{\beta _k}} \right|}^2} + {b_n}\left| {{\beta _k}} \right| + {c_n}}}{{{u_n}{{\left| {{\beta _k}} \right|}^2} + {v_n}}}}\\ {{\rm{s}}{\rm{.t}}{\rm{. }}\ {P_a}(\beta ) = \sum\limits_{n \in A} {{{\left| {{\beta _n}} \right|}^2}} \left( {P{{\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}} \right|}^2} + \delta _k^2} \right) \le P_a^{\max }} \end{array}, $ | (15) |
上述问题最大化的封闭解为
| $ {\left| {{\beta _k}} \right|^*} = \min \left\{ {\sqrt {\frac{{P_a^{\max } - \sum\limits_{i \in A, i \ne n} {{{\left| {{\beta _i}} \right|}^2}} \left( {P{{\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}} \right|}^2} + \delta _k^2} \right)}}{{\left( {P{{\left| {{\mathit{\boldsymbol{h}}_{{\rm{UR}}, n}}} \right|}^2} + \delta _k^2} \right)}}} , \frac{{{d_n}}}{{{b_n}}} + \sqrt {\frac{{d_n^2}}{{b_n^2}} + \frac{{{v_n}}}{{{u_n}}}} } \right\}。$ | (16) |
优化算法表述如下。
Algorithm 1:Latency minimization for IRS-aided MEC.
Input: Dk, hUB, hUR, hRB, Θ
Output: dk*, θ*, w*, 丨βk丨
1:K users request processing computing task offloading, task processing queue in order of request
2:Randomly generate αk satisfying constraints C3, C4
3:while objective value has not converged do
4: Calculate dk* according to the formula (9)
5: Calculate w* according to the formula (11)
6: Calculate θ* according to the formula (13)
7: if active intelligent reflecting surface units are deployed then
8: Calculate the optimal丨βk丨* according to the formula (16)
9: end if
10:end while
通过MATLAB平台仿真, 验证所提算法在智能反射面辅助的多用户边缘计算系统中的性能。仿真位置设置如图 2所示。
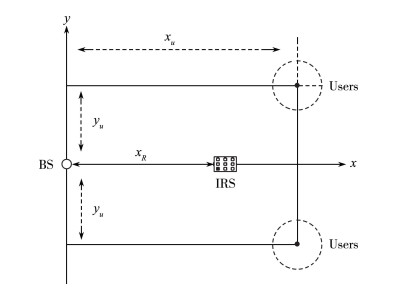 |
| 图 2 仿真场景设置 |
系统包括一个M天线并搭载MEC Server的BS, N个无源反射单元的IRS, A个有源反射的IRS, 辅助K个单天线Users处理计算任务, 单天线Users的位置随机分布在两个半径为r的区域内。假设在基站和用户处部署均匀线性阵列(uniform linear arrays, ULAs), 在IRS处部署N个单元的均匀平面阵列(uniform planar arrays, UPAs)。假设所有节点的阵列元件之间的距离为半波长, BS、IRS和Users的位置分别位于(0, 0), (xR, 0)和分别以(xu, yu), (xu, -yu)为圆心半径为r的小区内。其中设置xR=80 m, yu=10 m, r=5 m和xu={0, 10, 20, …, 160}。
信道都经历大尺度衰落和小尺度衰落, 大尺度衰落采用路径损耗模型, 即
| $ L(d) = {C_0}{\left( {\frac{d}{{{d_0}}}} \right)^{ - \alpha }}。$ | (17) |
其中, C0为d0=1 m的路径损耗, d为实际信道链路距离, α是路径损耗指数, 取值范围为2~4, 仿真验证中用户与BS、用户与IRS和IRS与BS间的路径损耗指数分别设置为3.5、2.2和2.2。对于小尺度衰落服从莱斯分布, 具体表示如下
| $ G = \sqrt {\frac{k}{{k + 1}}} {G^{{\rm{LOS}}}} + \sqrt {\frac{1}{{k + 1}}} {G^{{\rm{NLOS}}}}。$ | (18) |
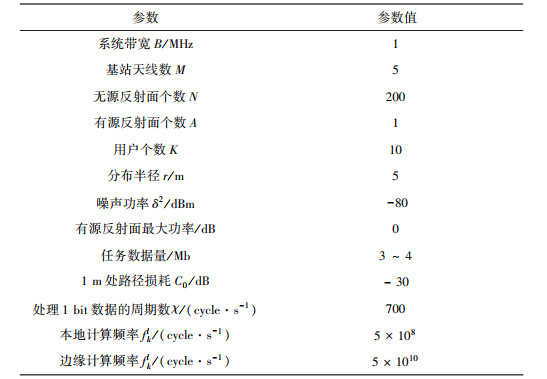
其中, k为莱斯因子, GNLOS为非视距部分, 服从瑞利分布, GLOS为视距部分, 视距分量由根据方位角和仰角离去角和到达角计算的阵列响应向量的乘积给出, 仿真参数设置如表 1所示。
| 表 1 仿真参数设置 |
 |
为了验证所提算法有效性, 通过对比以下方案来验证智能反射面相位和有源智能反射面对计算卸载时延的影响: (1)具有随机相位的传统无源IRS辅助的计算卸载时延(2)具有优化相位的传统无源IRS计算卸载时延(3)具有优化相位的无源IRS和有源IRS辅助的计算卸载时延。
3.2 仿真结果图 3给出了不同计算卸载模式下与用户时延之间的关系。Hybrid IRS, Optimized phase IRS, Random phase IRS分别表示N=200, A=1优化相位的智能反射面, N=200优化相位的无源智能反射面和N=200随机相位的无源智能反射面。由图 3可知, 随机相位的方案中, 系统计算时延随用户的距离增加而增加, 这种场景类似于实际传输场景。与只有无源的智能反射面的方案相比, 混合智能反射面在用户时延方面有更大的优势, 时延的变化随着用户靠近和远离IRS而呈现先下降后增加的趋势。无源优化相位智能反射面方案与混合智能反射面方案, 在时延表现方面, 用户在20~80 m距离间, 时延差距开始表现明显, 混合智能反射面方案达到2 ms时延优势, 用户在80~160 m距离间, 时延差距表现更加明显, 混合智能反射面方案达到10ms时延优势, 随着距离的增加, 混合智能反射面的优势更加凸显。
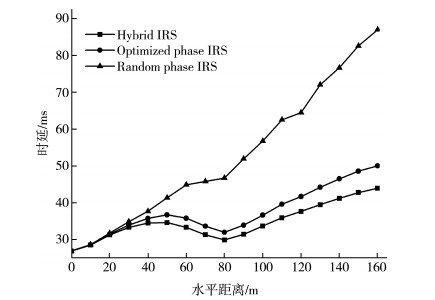 |
| 图 3 计算卸载时延随距离变化图 |
图 4给出了N=200时, 有源反射面个数与时延之间的关系。由图 4可知, 用户请求处理时延随有源智能反射面数量增加而降低。因为有源智能反射面通过放大入射信号幅度和相位, 改善了基站接收信号功率增益, 所以改善了系统传输性能。系统计算性能提升增幅与有源智能反射面数量关系上, 当有源智能反射面个数从0增加到1的过程是系统性能提升最多的, 有源智能反射面个数从1提升到10的过程对系统性能提升较少, 因此在实际的计算模型通过引入少量的有源智能反射面, 对系统的传输性能有很大的提升作用。
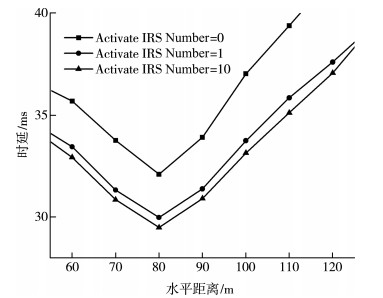 |
| 图 4 有源IRS对计算卸载时延影响 |
图 5给出了智能反射面个数与用户时延之间的关系。由图 5可知, 用户请求处理时延随智能反射面数量增加而降低。智能反射面控制器将更多路径的信号调整反射到接收端基站, 随着反射面数量的增加, 入射路径也增加, 从而使得系统的性能提升。通过合理的部署, 无线信道传输性能得到提升, 从而进一步提高系统边缘计算卸载效率。
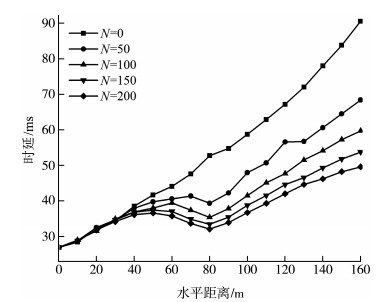 |
| 图 5 无源IRS对计算卸载时延影响 |
4 结论
考虑在有源智能反射面发射功率、无源智能反射面反射信号相位以及用户和边缘服务器计算频率的约束下, 通过交替优化算法优化智能反射面有源反射信号幅度和相位、无源反射信号相位和线性接收矢量和计算卸载变量, 分析了用户计算卸载时延最小化的问题。仿真表明通过优化卸载变量, 能够更好进行资源分配, 降低计算卸载时延, 通过在传统智能反射面中加入有源智能反射面, 能够明显降低用户的计算卸载时延。
| [1] |
孙巍, 宋清洋, 郭磊. 智能反射表面辅助的无线携能通信网络资源分配算法[J]. 通信学报, 2022, 43(2): 34-43. |
| [2] |
张慧雯. 面向移动网络的边缘计算卸载优化研究[D]. 北京: 北京邮电大学, 2021.
|
| [3] |
DI RENZO M, ZAPPONE A, DEBBAH, M, et al. Smart radio environments empowered by reconfigurable intelligent surfaces: how it works, state of research, and road ahead[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(11): 2450-2525. DOI:10.1109/JSAC.2020.3007211 |
| [4] |
BAI T, PAN C, DENG Y, et al. Latency minimization for intelligent reflecting surface aided mobile edge computing[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(11): 2666-2682. DOI:10.1109/JSAC.2020.3007035 |
| [5] |
ZHANG W, WEN Y, GUAN K, et al. Energy-optimal mobile cloud computing under stochastic wireless channel[J]. IEEE Transactions on Wireless Communications, 2013, 12(9): 4569-4581. DOI:10.1109/TWC.2013.072513.121842 |
| [6] |
WANG Y, SHENG M, WANG X, et al. Mobile-edge computing: partial computation offloading using dynamic voltage scaling[J]. IEEE Transactions on Communications, 2016, 64(10): 4268-4282. |
| [7] |
HUANG C, ZAPPONE A, ALEXANDROPOULOS G, et al. Reconfigurable intelligent surfaces for energy efficiency in wireless communication[J]. IEEE Transactions on Wireless Communications, 2019, 18(8): 4157-4170. DOI:10.1109/TWC.2019.2922609 |
| [8] |
DU Y, YANG K, WANG K, et al. Joint resources and workflow scheduling in uav-enabled wirelessly-powered mec for iot systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(10): 10187-10200. DOI:10.1109/TVT.2019.2935877 |
| [9] |
GOLDSMITH A. Wireless communications[M]. Cambridge, U.K.: Cambridge Univ.Press, 2005: 199-200.
|
| [10] |
CHU Z, XIAO P, SHOJAFAR M, et al. Intelligent reflecting surface assisted mobile edge computing for internet of things[J]. IEEE Wireless Communications Letters, 2021, 10(3): 619-623. DOI:10.1109/LWC.2020.3040607 |
 2023, Vol. 37
2023, Vol. 37


