| 基于MATLAB的掌静脉图像增强方法研究 |
图像处理是模式识别一个重要的准备过程。随着计算机技术的发展, 人们对数字图像处理技术的研究越来越深入[1-2]。数字图像处理是通过计算机对图像进行去除噪声、增强、复原、分割、特征提取等处理的方法和技术[3]。通常采集掌静脉图像过程中, 由于噪声、光照等外界环境、采集装置自身的原因[4], 或者采集对象的操作问题, 采集到的掌静脉图像往往不理想, 经常出现图像模糊、图像对比度低, 图像中细节不清晰等问题[5], 严重影响了掌静脉识别的准确率和速度, 因此在提取掌静脉特征信息之前要对掌静脉图像进行预处理增强, 使增强后得到的图像细节特征更清晰、更容易被识别。
图像增强分为基于空域的算法和基于频域的算法[6]。基于空域的算法直接对灰度级做运算[7], 分为点运算和邻域去噪算法[8]。点运算是对每一个像素点进行计算, 按照一定的映射方法将原亮度变换到指定范围或整个动态区域, 而与其他像素点无关。它能使图像像素范围扩大, 使得图像对比度更好, 从而更容易辨识。在某些特定的应用场合, 可以抑制不感兴趣的区域、突出目标区域, 从而扩大目标与周围背景的差距, 以满足特定的需求。点运算包含灰度级校正线性变换和直方图修正等[9]。本文对点运算中的线性变换算法和直方图均衡算法进行研究, 将它们应用于掌静脉图像的图像增强, 并通过MATLAB进行了仿真测试。
1 线性变换图像增强方法及其MATLAB实验图像在成像过程中, 常常会因为曝光不足或曝光过度导致图像过亮或过暗使得图像的灰度值分布在一个集中的范围[10-11], 图像的对比度低、图像细节不清晰[12]。因此将图像的灰度按照线性变换函数进行线性扩展便可以改善图像质量、提高辨识度, 线性变换的方法是一种直接对比度增强方法。例如一图像的灰度范围为[a, b], 用线性变换将灰度范围扩大到[c, d], 可按照以下公式对每一个像素点做线性变换。
| $ g(x, y) = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} c&{, 0 \le f(x, y) < a}\\ {\frac{{d - c}}{{b - a}}f(x, y) + c}&{, a \le f(x, y) < b}\\ d&{, b \le f(x, y) \le 255} \end{array}\\ \end{array} \right. $ | (1) |
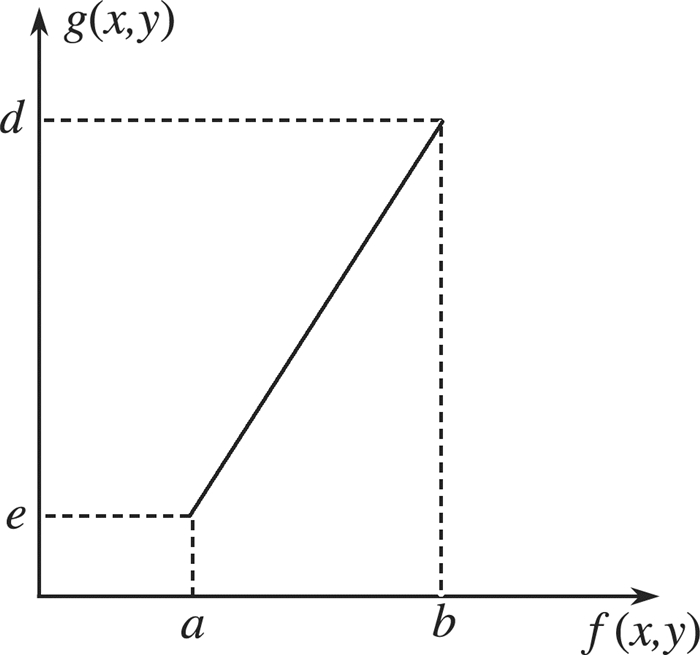 |
| 图 1 线性变换 |
其中f(x, y)为原图像像素值, g(x, y)为变换后的图像像素值。将其应用到掌静脉图像的增强:
I=imread('1.bmp'); %导入图像
[m, n]=size(I); %获取原图像矩阵的行列数
J=zeros(m, n); %定义一个元素全为零的新矩阵用来放变换后的图像
subplot(1, 2, 1), imshow(I); title('原始图像'); %显示原图像
a=70;%确定像素变换范围
b=170;
c=60;
d=180;
K=(d-c)/(b-a); %求变换斜率
for i=1:m; %用两重循环进行灰度线性变换
for j=1:n;
if I(i, j) < 60
J(i, j)=c;
else if I(i, j)>=60&&I(i, j) < 150
J(i, j)=K*I(i, j);
else
J(i, j)=d;
end
end
end
end
A=uint8(J); %将数据变成无符号的8位整型数据
subplot(1, 2, 2), imshow(A); title('线性拉伸图像'); %显示线性拉伸后的图像
运行结果如下:
由图 2可以看出, 线性变换前, 掌静脉图像灰度集中且较暗, 灰度动态范围小, 图像细节不清晰。经过线性拉伸, 图像整体亮度提高, 图像的灰度范围有所增大, 图像整体平淡的情况有所改善, 图像细节特征较原图更清晰。
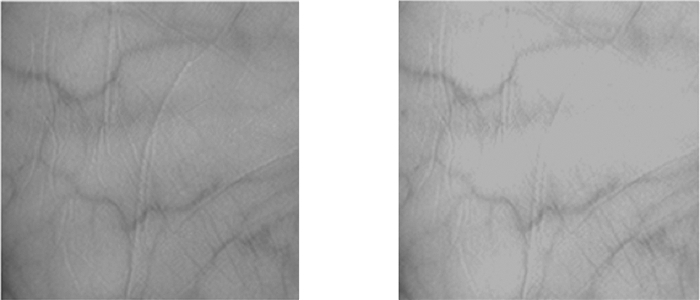 |
| 图 2 原图像(左)与线性拉伸算法处理效果图(右) |
上述线性变换为无差别的、均匀拉伸的线性变换, 在实际应用中, 通常需要对某些感兴趣的区域或图像细节部分进行拉伸, 对不需要的部分进行压缩, 则可以用到分段线性函数。即把灰度值范围分成多个区间, 每个区域分别作线性变换。常用的分段线性变换如下:
| $ g(x, y)=\left\{\begin{array}{cc} {\frac{c}{a} f(x, y)} & {, 0 \leqslant f(x, y)<a} \\ {\frac{d-c}{b-a}[f(x, y)-a]+c} & {, a \leqslant f(x, y)<b} \\ {\frac{M_{f}-z}{M_{f}-b}[f(x, y)-b]+d} & {, b \leqslant f(x, y) \leqslant M} \end{array}\right. $ | (2) |
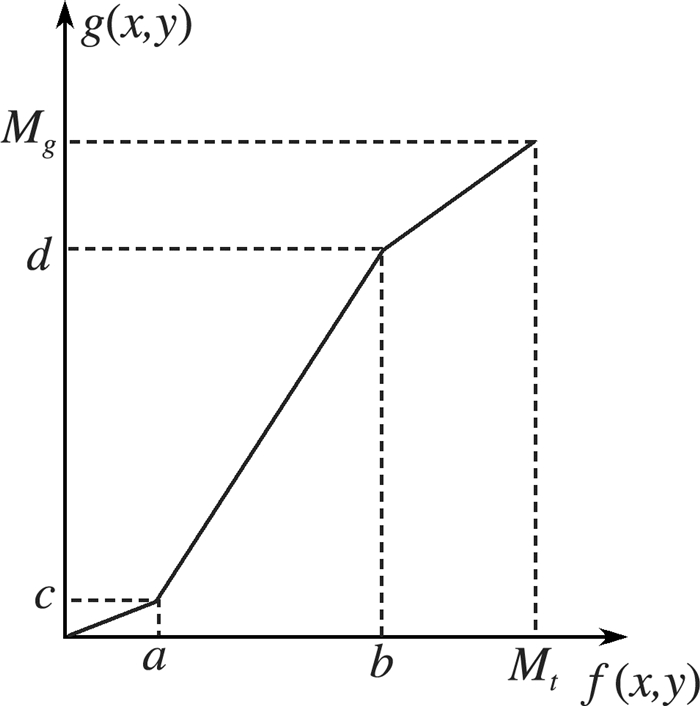 |
| 图 3 分段线性变换 |
经过分段线性变换, [0, a)和[b, M]之间的像素动态范围变小, 图像被压缩, [a, b)之间的像素经过变换动态范围增大, 图像被突出。通过调整节点值以及斜率的大小可灵活地对图像进行拉伸。
将其应用到掌静脉图像增强:
I=imread('1.bmp'); %导入原图像
[m, n]=size(I); %获取原图像矩阵的行列数
J=zeros(m, n); %定义新的矩阵存放变换后的图像矩阵
subplot(1, 2, 1), imshow(I); title('原始图像');
%将1行2列的第1个区域显示原图像
a=70;%节点参数设置
b=140;
c=60;
d=170;
k1=c/a; %求三段斜率
k2=(d-c)/(b-a);
k3=(255-d)/(255-b);
for i=1:m; %用双重循环进行分段线性拉伸
for j=1:n;
if I(i, j) < 80
J(i, j)=k1*I(i, j);
else if I(i, j)>=80&&I(i, j) < 140
J(i, j)=k2*(I(i, j)-a)+c;
else
J(i, j)=k3*(I(i, j)-b)+d;
end
end
end
end
A=uint8(J); %将数据变为8位无符号整型数据
subplot(1, 2, 2), imshow(A); title('分段线性拉伸图像');
%将1行2列的第2个区域显示分段线性拉伸后的图像
运行结果如下:
由图 4可以看出, 分段线性变换将原图中最暗和最亮的小部分进行压缩, 而将含有大部分特征信息的中间区域进行突出, 突出部分的对比度明显增强, 细节信息较原图清晰很多。
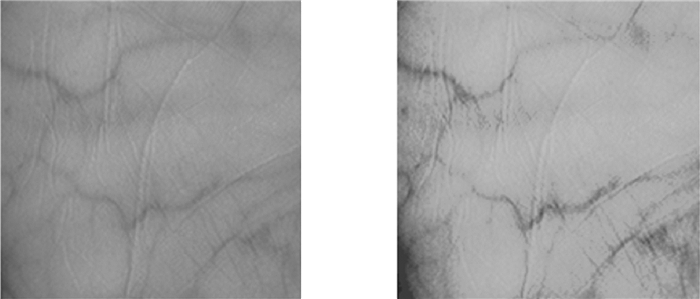 |
| 图 4 原图像(左)与分段线性拉伸处理效果图(右) |
2 直方图均衡化图像增强方法及其MATLAB实验
直方图是图像处理的重要工具, 它能用很少的数据表达图像灰度的统计特征[13], 它统计的是图像的各个灰度级出现的次数或概率[14]。改变了直方图中灰度级的分布也就是改变了图像。直方图均衡化就是基于直方图的统计特征, 重新分配图像像元值, 使一定范围内像元值的数量大致相等[15]。这样可以防止灰度值集中于某个小范围而对比度低, 增加了像素值的动态范围, 从而使图像细节更清晰, 是一种间接增强对比度的方法。
直方图均衡化算法的计算过程如下:
1) 计算原始图像的直方图
将原始图像灰度值划分为L个灰度级, 并统计每个灰度级像素数nk。则原始直方图各概率为P(rk)=nk/N(k=0, 1, 2, …L-1)。其中rk为第k个灰度级, N为总像素数。
2) 将原函数的灰度级rk映射到新的灰度级sk。
累计分布函数sk=∑pk。对sk取整sk=int{(L-1)sk+0.5}, 则灰度级映射对应关系rk→sk。
3) 计算新直方图
统计新直方图各灰度级像素nk, 用pk(sk)=nk/N计算新的直方图。
MATLAB工具箱中提供了直方图均衡化的histeq()函数, 将其应用于掌静脉图像, 如下:
I=imread('1.bmp'); %读取图像
J=histeq(I); %进行直方图均衡化
subplot(2, 2, 1), imshow(I); %在2行2列的第1个区域显示原始图像
title('原始图像');
subplot(2, 2, 2), imhist(I); %在2行2列的第2个区域显示原图像直方图
title('原图像直方图');
subplot(2, 2, 3), imshow(J); %在2行2列的第3个区域显示均衡化后的图像
title('均衡化后的图像');
subplot(2, 2, 4), imhist(J); %在2行2列的第4个区域显示均衡化后的直方图
title('均衡化后图像的直方图');
运行结果如下:
由图 5可以看出, 变换后的图像对比度显著增强, 亮度也增加了; 变换前直方图分布比较集中, 变换后直方图分布比较均匀。
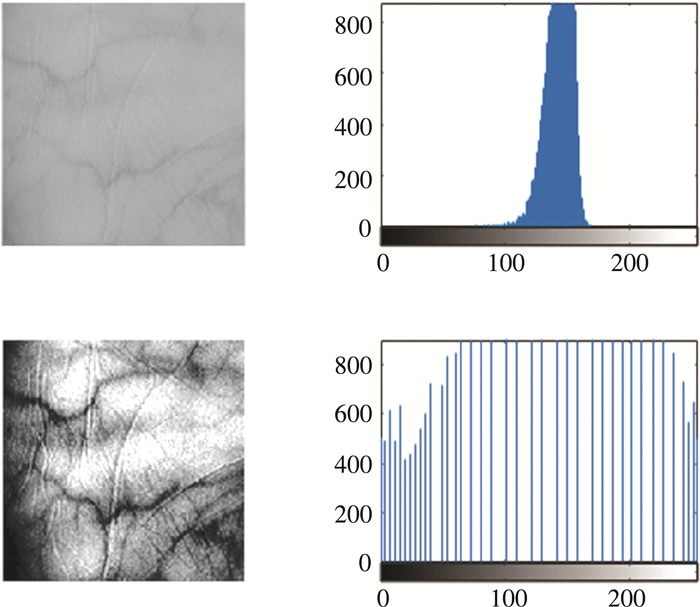 |
| 图 5 原图像(左上)、原图像直方图(右上)、均衡化后的图像(左下)、均衡化处理后的图像直方图(右下) |
直方图均衡化是基于图像全局进行的变换, 虽然增强了图像整体的对比度, 但是不能有效提高图像中某局部对比度、突出某些重要特征, 在某些对局部细节信息要求较高的场合不能很好地发挥作用。为解决这个问题, 将原图像划分成若干个子块, 分别对每一个小块进行直方图均衡化, 并通过双线性插值法把各个小块拼接起来, 提高运算速度, 这就是限定对比度适应性直方图均衡化。MATLAB工具箱中提供了限制对比度适应性直方图均衡化的adapthisteq()函数, 将其应用于掌静脉图像, 如下:
I=imread('1.bmp'); %读取原图像
subplot(1, 3, 1), imshow(I);
title('原始图像'); %在1行3列的第1个区域显示原图像
J=histeq(I); %对原图像进行均衡化操作
subplot(1, 3, 2), imshow(J);
title('直方图均衡图像'); %在1行3列的第2个区域显示直方图均衡图像
K=adapthisteq(I); %对原图像进行限制对比度自适应均衡操作
subplot(1, 3, 3), imshow(K);
title('限制对比度自适均衡图像'); %在1行3列的第3个区域显示限制对比度均衡后的图像
运行结果如下:
由图 6可以看出, 直方图均衡与限制对比度适应性均衡都能显著提高图像对比度, 但是其中限制对比度适应性均衡选择性地对掌静脉纹理特征进行增强, 使图像更清晰, 细节特征更显著。
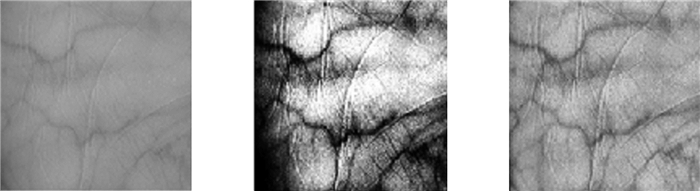 |
| 图 6 原图像(左)、直方图均衡处理后的图像(中)、限制对比度适应性均衡处理后的图像(右) |
3 结论
本文对图像增强中的线性变换方法、分段线性变换方法、直方图均衡方法以及限制对比度适应性直方图均衡方法应用于掌静脉图像的增强, 通过MATLAB的仿真实验可以得出以下结论:
线性变换、分段线性变换均能调节图像对比度, 变换后的对比度增加, 图像质量有所提升; 直方图均衡对整个图像使用相同的变换进行对比度调节, 能显著改善图像质量。此方法适用于像素值分布比较均衡、都太亮或太暗的图像, 但满足不了对图像局部的细节要求高的场合; 限制对比度适应性直方图均衡方法能通过重新分配亮度来调节图像对比度, 该方法更适用于改进图像局部对比度以获得更多图像细节的情况。
| [1] |
章化冰, 凌坚, 练益群. 基于模板匹配的马赛克视频检测方法研究[J]. 中国有线电视, 2010, 11: 1254-1256. DOI:10.3969/j.issn.1007-7022.2010.11.006 |
| [2] |
张楠楠, 刘伟, 王伟. 玉米霉变及黄曲霉素的图像处理检测方法[J]. 中国粮油学报, 2014, 2(29): 82-87. |
| [3] |
唐晓娜.基于样本块的大范围图像修补技术的研究与实现[D].上海: 华东师范大学, 2008.
|
| [4] |
吴艳.基于FPGA的数字图像处理基本算法研究与实现[D].哈尔滨: 哈尔滨工业大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10359-1015710037.htm
|
| [5] |
王晶.水下图像增强与复原研究办法[D].河北: 燕山大学, 2018.
|
| [6] |
聂超.基于直方图的高效图像增强算法研究[D].杭州: 杭州电子科技大学, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D485127
|
| [7] |
马琳, 于宁. 数字图像增强算法分析[J]. 交通科技与经济, 2011, 1(13): 122-125. |
| [8] |
郑秀华.基于MATLAB的图像增强处理方法[D].福建泉州: 华侨大学, 2014.
|
| [9] |
刘万程.基于Visual C++的数字图像处理[D].大连: 大连海事大学, 2014.
|
| [10] |
戈志伟, 姚素英, 徐江涛. 一种应用于CMOS传感器的快速自动曝光控制方法[J]. 天津大学学报, 2010, 10(43): 854-859. |
| [11] |
晁目力, 朱名日, 庄严. 一种高清网络摄像机自动曝光的方法[J]. 桂林电子科技大学学报, 2012, 5(32): 135-138. |
| [12] |
张临临, 基于图像分层和动态压缩的图像细节压缩研究方法[D].西安: 西安电子科技大学, 2013.
|
| [13] |
赵小川, 何灏, 缪远诚. MATLAB数字图像处理实战[M]. 北京: 机械工业大学出版社, 2013: 128-136.
|
| [14] |
赵晓红, 沈绪榜, 张艳宁, 等. 直方图计算的数据并行实现办法[J]. 信号处理, 2005, 21(2): 111-114. DOI:10.3969/j.issn.1003-0530.2005.02.001 |
| [15] |
刘成龙. 精通MATLAB图像处理[M]. 北京: 清华大学出版社, 2015: 267.
|
 2019, Vol. 33
2019, Vol. 33


