| 扩散方程Crank-Nicolson格式的稳定性 |
关于扩散方程Crank-Nicolson格式的研究已有大量结果, 文献[1]构造了扩散系数为1时的一维和二维抛物方程的Crank-Nicolson格式, 并证明它是阶数为二的无条件稳定的差分格式; 文献[2]把二维Crank-Nicolson格式, 由常系数推广到变系数情形, 并证明了它是阶数为二的无条件稳定的差分格式。稳定性作为数值格式的一种属性, 在某种意义下, 格式的稳定性与一致性相结合, 就可以推出数值格式对于原问题的估计的收敛性。而一致性易于验证, 从而研究稳定性是得到收敛性的主要工作。P.D.Lax借助泛函分析的工具, 对一类很广的初值问题证明了差分格式解的收敛性和稳定性的等价定理[3]。J.Douglas采用初等的方法讨论了具体问题, 得到了收敛速度的估计[4]。李荣华综合了Lax和Douglas工作的优点, 给出Lax等价定理的一个初等证明, 去掉了关于初值问题的适定性要求和简化了Douglas的证明[5]。而本文研究的任意正常数的扩散系数的Crank-Nicolson差分格式不仅是无条件稳定的, 而且误差较小, 计算速度快。
1 扩散方程的解析解考虑常系数扩散方程
| $ \left\{\begin{array}{l} u_{t}=a u_{x x}, \quad 0<x<1, t>0, \\ u(x, 0)=g(x), \quad 0 \leqslant x \leqslant 1, \\ u(0, t)=u(1, t)=0, \quad t>0, \end{array}\right. $ | (1) |
其中a为正常数且g(x)不恒为零。
令u(x, t)=h(x)p(t)且是方程(1)的充分光滑解, 所以u(x, 0)=h(x)p(0)=g(x), 由于g(x)不恒为零, 那么h(x)=g(x)/p(0), 进而
| $ \frac{\partial u}{\partial t}=h(x)=\frac{d p}{d t}=\frac{1}{p(0)} g(x) \frac{d p}{d t}, $ |
| $ \frac{\partial^{2} u}{\partial x^{2}}=p(t) \frac{d^{2} h}{d x^{2}}=p(t) \frac{1}{p(0)}, \frac{d^{2} g}{d x^{2}}, $ |
由扩散方程(1)得
| $ \frac{d p}{p}=\frac{a}{g} \frac{d^{2} g}{d x^{2}} d t, $ |
它的解是
| $ p(t)=c \exp \left(\frac{a}{g} \frac{d^{2} g}{d x^{2}} t\right), $ |
其中c是任意常数, 故扩散方程的解析解为
| $ u(x, t)=g(x) \exp \left(\frac{a}{g} \frac{d^{2} g}{d x^{2}} t\right)。$ | (2) |
从u(x, t)的表达式可以看出扩散方程(1)解析解的正负性完全由g(x)的正负性控制。
2 差分格式的建立将区域[0, 1]×(0, +∞)沿x轴和t轴方向进行矩形剖分, 其中空间步长为Δx=h=1/J, 时间步长为Δt=τ, 网格点(xj, tn)记作
| $ x_{j}=j \varDelta x=j h, j=0,1, \cdots, J , $ |
| $ t_{n}=n \varDelta t=n \tau, n=0,1,2, \cdots。$ |
在点(xj, tn+1/2)用一阶中心差商逼近
| $ \begin{array}{l} \frac{u_{j}^{n+1}-u_{j}^{n}}{\tau}=\frac{a}{2}\left\{\frac{u_{j+1}^{n+1}-2 u_{j}^{n+1}+u_{j-1}^{n+1}}{h^{2}}+\right.\\ \left.\frac{u_{j+1}^{n}-2 u_{j}^{n}+u_{j-1}^{n}}{h^{2}}\right\},\end{array} $ | (3) |
初值条件和边值条件离散为
| $ u_{j}^{0}=g_{j},$ | (4) |
| $ u_{0}^{n}=u_{J}^{n}=0,$ | (5) |
且该格式的截断误差为O(τ2+h2), 当τ和h都趋于零时, O(τ2+h2)也趋于零, 所以该差分格式满足相容性。
引理1:差分格式ujn+1=C(xj, τ)ujn稳定的必要条件是τ≤τ0, nτ≤T, 对所有k∈R有
| $ \left|\lambda_{j}(G(\tau, k))\right| \leqslant 1+M \tau, j=1,2, \cdots, p,$ | (6) |
其中,λj(G(τ, k))表示增长矩阵G(τ, k)的特征值;M为常数。条件(6)被称为von Neumann条件。
引理2:如果差分格式的增长矩阵G(τ, k)是正规矩阵, 则von Neumann条件是差分格式稳定的充要条件。
引理3:如果差分格式un+1=Aun的矩阵A是一个正规矩阵, 则谱半径条件
| $ \rho(A) \leqslant 1+M \tau $ |
是差分格式稳定的一个充分必要条件。其中M为常数, un=(u1n, u2n, …, unJ-1)T。
3 Fourier方法定理1:若a为正常数且gj在网格点上有意义, 存在常数τ0>0, 使得当τ≤τ0, nτ≤T时, 则对所有k∈R, 扩散方程(1)的Crank-Nicolson格式(3)-(5)是无条件稳定的。
证明: 将(3)式改写为
| $ \begin{aligned} &(1+a \lambda) u_{j}^{n+1}-\frac{a \lambda}{2} u_{j+1}^{n+1}-\frac{a \lambda}{2} u_{j-1}^{n+1}= \\ &(1+a \lambda) u_{j}^{n}+\frac{a \lambda}{2} u_{j+1}^{n}+\frac{a \lambda}{2} u_{j-1}^{n},\end{aligned} $ | (7) |
其中λ=τ/h2。令ujn=vneikjh, 并带入上式, 得
| $ \begin{array}{l} \ \ \ \ \ \ (1+a \lambda) v^{n+1} e^{i k j h}-\frac{a \lambda}{2} v^{n+1} e^{i k(j+1) h}- \\ \frac{a \lambda}{2} v^{n+1} e^{i k(j-1) h}=(1+a \lambda) v^{n} e^{i k j h}+\frac{a \lambda}{2} v^{n} e^{i k(j+1) h}+ \\ \frac{a \lambda}{2} v^{n} e^{i k(j-1) h}, \end{array} $ |
消去公因子有
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \left(2(1+a \lambda)-a \lambda e^{i k h}-a \lambda e^{-i k h}\right) v^{n+1}= \\ \left(2(1+a \lambda)+a \lambda e^{i k h}+a \lambda e^{-i k h}\right) v^{n}, \end{array} $ |
化简得
| $ \begin{array}{l} \ \ \ \ \ \ \ \ (1+a \lambda-a \lambda \cos k h) v^{n+1}=(1-a \lambda+ \\ a \lambda \cos k h) v^{n}, \end{array} $ |
由此得增长因子
| $ \begin{array}{l} \ \ \ \ \ \ \ \ G(\tau, k)=(1-a \lambda+a \lambda \cos k h) /(1+a \lambda- \\ a \lambda \cos k h), \end{array} $ |
所以有
| $ \begin{aligned} G(\tau, k)=&\left(1-2 a \lambda \sin ^{2} \frac{k h}{2}\right) / \\ &\left(1+2 a \lambda \sin ^{2} \frac{k h}{2}\right), \end{aligned} $ |
因为a>0, λ>0, 所以G(τ, k)≤1, 那么G(τ, k)n≤1, 又Crank-Nicolson格式是常系数差分格式, 由引理1和引理2知Crank-Nicolson格式(3)-(5)是无条件稳定的。
4 矩阵方法(直接方法)定理2:若a为正常数且gj在网格点上有意义, 存在常数τ0>0, 使得当τ≤τ0, nτ≤T时, 则扩散方程(1)的Crank-Nicolson格式(3)-(5)是无条件稳定的。
证明: 可以把(7)式写为向量形式, 即
| $ \begin{aligned} &\left[\begin{array}{cccc} 1+a \lambda & -a \lambda / 2 & & \\ -a \lambda / 2 & 1+a \lambda & \ddots & \\ & \ddots & \ddots & -a \lambda / 2 \\ & & -a \lambda / 2 & 1+a \lambda \end{array}\right] .\\ &\left[\begin{array}{c} u_{1}^{n+1} \\ u_{2}^{n+1} \\ \vdots \\ u_{J-1}^{n+1} \end{array}\right]+\left[\begin{array}{c} u_{1}^{n+1} \\ 0 \\ \vdots \\ u_{J}^{n+1} \end{array}\right]=\\ &\left[\begin{array}{cccc} 1-a \lambda & a \lambda / 2 & & \\ a \lambda / 2 & 1-a \lambda & \ddots & \\ & \ddots & \ddots & a \lambda / 2 \\ & & a \lambda / 2 & 1-a \lambda \end{array}\right]\left[\begin{array}{c} u_{1}^{n} \\ u_{2}^{n} \\ \vdots \\ u_{J-1}^{n} \end{array}\right]+\\ &\left[\begin{array}{c} u_{1}^{n} \\ 0 \\ \vdots \\ u_{J}^{n} \end{array}\right] 。\end{aligned} $ | (8) |
若令
| $ u^{n}=\left(u_{1}^{n}, u_{2}^{n}, \cdots, u_{J-1}^{n}\right)^{T}, $ |
因为u0n=uJn=0, 则(8)式可以写为
| $ A u^{n+1}=B u^{n}, $ | (9) |
其中
| $ A=\left[\begin{array}{cccc} 1+a \lambda & -a \lambda / 2 & & \\ -a \lambda / 2 & 1+a \lambda & \ddots & \\ & \ddots & \ddots & -a \lambda / 2 \\ & & -a \lambda / 2 & 1+a \lambda \end{array}\right], $ |
| $ B=\left[\begin{array}{cccc} 1-a \lambda & a \lambda / 2 & & \\ a \lambda / 2 & 1-a \lambda & \ddots & \\ & \ddots & \ddots & a \lambda / 2 \\ & & a \lambda / 2 & 1-a \lambda \end{array}\right] \text { 。} $ |
令C=A-1B, 则(9)式可以写为
| $ u^{n+1}=A^{-1} B u^{n}=C u^{n}。$ |
令J-1阶方阵
| $ S=\left[\begin{array}{ccccc} 0 & 1 & & & \\ 1 & 0 & 1 & & \\ & \ddots & \ddots & \ddots & \\ & & 1 & 0 & 1 \\ & & & 1 & 0 \end{array}\right], $ |
则A和B可以表示为
| $ A=(1+a \lambda) E-\frac{a \lambda}{2} S , $ |
| $ B=(1-a \lambda) E+\frac{a \lambda}{2} S, $ |
其中E是J-1阶单位矩阵。
又因为矩阵S的特征值[6]为2coskhπ, 所以A的特征值为1+aλ-aλcoskhπ, B的特征值为1-aλ+aλcoskhπ, 从而矩阵C的特征值为
| $ \frac{1-a \lambda+a \lambda \cos k h \pi}{1+a \lambda-a \lambda \cos k h \pi}, k=1,2, \cdots, J-1, $ |
又矩阵C为对称矩阵, 从而C为正规矩阵, 所以对任意的aλ矩阵C的谱半径都有
| $ \begin{gathered} \rho(C)=\max \limits_{1 \leqslant k \leqslant J-1}\left|\frac{1-a \lambda+a \lambda \cos k h \pi}{1+a \lambda-a \lambda \cos k h \pi}\right| \\ =\max \limits_{1 \leqslant k \leqslant J-1}\left|\frac{1-a \lambda(1-\cos k h \pi)}{1+a \lambda(1-\cos k h \pi)}\right| \\ \leqslant 1, \end{gathered} $ |
由于问题是线性的, 故由引理3知Crank-Nicolson格式(3)-(5)是无条件稳定的。
5 数值例子为验证式(3)-(5)的稳定性, 考虑初边值问题
| $ \left\{\begin{array}{l} u_{t}=a u_{x x}, \quad 0<x<1, t>0, a>0, \\ u(x, 0)=\sin \pi x, \quad 0 \leqslant x \leqslant 1 ,\\ u(0, t)=u(1, t)=0, \quad t>0, \end{array}\right. $ | (10) |
根据式(2)可知解析解为
| $ u(x, t)=e^{-\pi^{2} t} \sin \pi x, 0 \leqslant x \leqslant 1, t \geqslant 0。$ |
取h=0.02, τ=0.002 5, λ=τ/h2=6.25为网格比。对不同的系数a, 用Crank-Nicolson格式求出扩散方程(10)在(0.4, 0.02)数值解, 并将它们与解析解的值加以比较。
表 1给出了当网格比λ=6.25时不同系数a下的精确解和数值解, 从表中不仅能看出误差较小, 同时也验证了格式满足2阶的收敛精度。
| 表 1 数值解与解析解间的比较 |
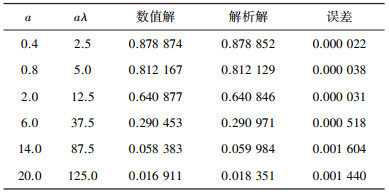 |
从图 1和图 2可以看出, 式(3)-(5)的数值解与精确解的吻合度很好。以上结论均表明Crank-Nicolson格式是无条件稳定的。
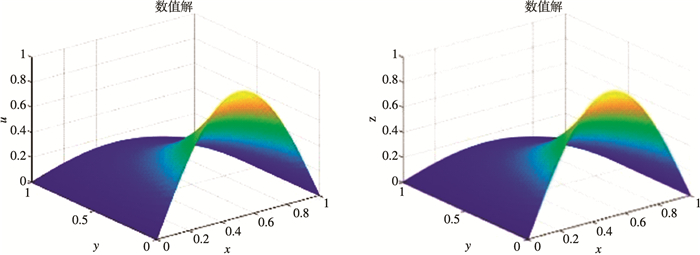 |
| 图 1 aλ=0.2时的数值解和解析解 |
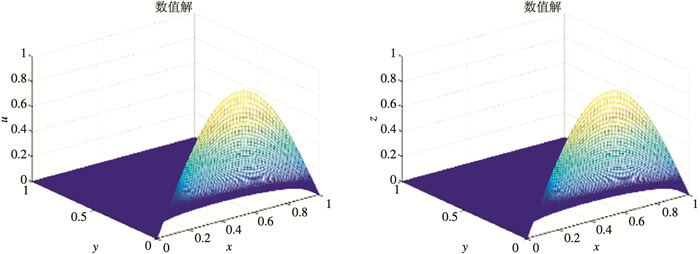 |
| 图 2 aλ=2.0时的数值解和解析解 |
| [1] |
李华, 周维奎, 邓培智. Crank-Nicolson差分格式及其稳定性研究[J]. 矿物岩石, 1998(S1): 3-5. |
| [2] |
卢玉蓉, 何永富, 蔡靖疆, 等. 二维Crank-Nicolson差分格式及其稳定性[J]. 成都理工学院学报, 1999(1): 67-70. |
| [3] |
RICHTMYER R D, MORTON K W. Difference methods for initial value problems[M]. New York: Interscience, 1967.
|
| [4] |
DOUGLAS J. On the relation between stability and convergence in the numerical solution of linear parabolic and hyperbolic differential equations[J]. Journal of the Society for Industrial and Applied Mathematics, 1956(4): 20-37. |
| [5] |
李荣华. 研究差分格式收敛性和稳定性的直接方法[J]. 吉林大学自然科学学报, 1962(1): 73-82. |
| [6] |
陆金甫, 关治. 偏微分方程数值解. 第3版[M]. 北京: 清华大学出版社, 2016.
|
 2021, Vol. 35
2021, Vol. 35


