| 基于语义对称分解哈希的快速ECG信号检测 |
随着社会的进步与发展, 大众对智慧医疗服务需求的提升使传统的医疗服务体系已经无法满足人民对医疗保健的迫切需要, 结合大数据、机器学习、深度学习等的智能医疗为此开辟了新的路径。心电图信号识别问题是医学诊断与人工智能相结合的一个热点问题。ECG可以及早的检测出心律不齐、早搏以及急性心肌梗死等多种心脏疾病, 是心血管疾病诊断的重要依据。心电图信号包含心脏病变的基本信息, 特征是五个被称为基准点的峰值, 以字母P、Q、R、S和T表示, 如图 1所示。QRS波是左右心室的去极化, 用作信号分析的参考点。P波是心房去极化的结果, 而心室引起其余的波峰。信号的筛查、诊断和检测依赖于波的形态, 以及每个峰值的持续时间和组成它的片段。例如, 当QRS波变大变宽时, 可能发生室性早搏。
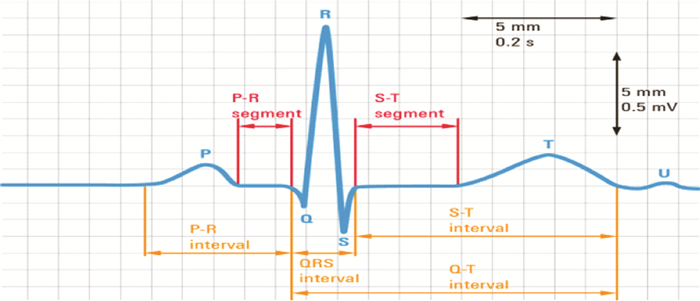 |
| 图 1 心电信号特征波段 |
1 研究现状
深度学习和医学的结合, 已经成为智能医疗领域的重要研究课题和新的发展趋势。目前除了QRS波定位检测算法已经足够成熟可靠外, 其它波段的定位算法可靠性都不高。如果不能对这些波段进行精准定位, 那将在很大程度上影响分类器精度。现在大多数采用传统机器学习框架的论文都采用了这样一种方法: 使用一些数学变换处理ECG信号, 得到较少的系数, 用这些系数来表征心拍, 从而实现对异常信号的检测。王莉莎等[1]基于小波张量化与Tucker分解的ECG分类算法: 将心电信号分帧后进行小波分解;张宇微等[2]采用了随机森林、K-近邻和C4.5三种传统机器学习算法和卷积神经网络算法在MIT-BIH心律不齐数据库上进行了验证分析;孙梦莉等[3]使用基于深度卷积网络结合迁移学习的分类判别算法, 在小数据样本中获得了较好分类性能;瞿文凤等[4]将深度学习技术应用于心电信号的分类识别研究, 提出基于DBN和CNN的心电信号分类方法;Hasan等[5]利用经验模式分解对ECG信号分解去噪, 并使用一维卷积网络对ECG信号特征进行提取和分类。上述方法也存在几个主要不足: 首先是仅使用深度学习模型, 不能充分利用ECG信号特征的多样性;其次是对心拍的分类需要将ECG信号的心拍进行分割[6], 耗时长, 效率低;最后是难以做到数据扩充以提高精度, 易受噪音干扰。针对以上问题, 本文提出一种基于语义对称分解哈希的快速ECG信号检测模型。
2 语义对称分解哈希 2.1 SSDH算法概述哈希得益于逐位XOR操作, 具有占用内部存储小、速度快、准确率高等特点, 被广泛地应用于机器视觉当中。基于哈希的检索方法旨在将具有高维特征、高存储量的数据通过哈希编码来表示, 这既降低了存储空间又提高了检索的效率。基于监督信息的哈希学习因利用监督信息来进行哈希学习, 往往具有更高的检索精度, 监督离散哈希的目标在于利用哈希函数将哈希码回归到其相应的标签上来生成哈希编码库, 从而实现快速的检索目的[7]。
虽然哈希计算简单, 特别适合大规模数据检索, 但是由于其二值的离散约束, 常常遭遇混合整数优化难题。针对该问题, 很多文献将哈希的离散约束松弛为连续变量, 但是这会造成量化损失。部分离散的哈希方法[8]通过交替优化和离散循环坐标下降方法有效地解决了该难题, 但是需要一码一码的学习哈希编码, 非常费时, 效率很低。为此, 我们提出一种快速的语义对称分解哈希算法(SSDH), 利用ECG标签, 生成语义相似矩阵, 再借助于Hadamard矩阵对已有的标签进行重排, 无需任何的迭代和参数调节就能快速生成哈希编码库。最后设计相应的哈希函数, 即可快速的实现ECG信号检测, 具体的流程框图如图 2所示。
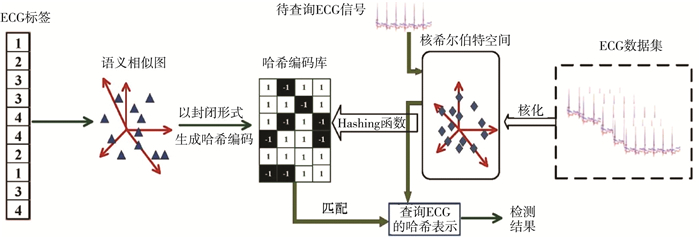 |
| 图 2 快速的SSDH算法流程框 |
2.2 算法实现
给定ECG的样本数据集
| $ {{s}_{ij}}=\left\{ \begin{array}{*{35}{l}} 1, \text{ }if\ \ \ {{y}_{i}}={{y}_{j}}, \\ 0, \text{ }otherwise. \\ \end{array} \right. $ | (1) |
然后对语义相似S进行离散的哈希分解, 直接生成哈希库B=[b1, b2, ⋯, bn]T∈{-1, 1}n×k, 其中k表示预设的哈希编码长度, 矩阵的每一行代表每个ECG信号的哈希编码。具体目标可以描述为:
| $ \begin{aligned} &\min J(B)=\left\|k S-B B^{T}\right\|_{F}^{2} \\ & s.t. B^{T} B=n I_{k}, B \in\{-1, 1\}^{n \times k} . \end{aligned} $ | (2) |
其中, ‖ ‖F表示矩阵Frobenius范数, 正交约束的目的是使得每一码的哈希特征尽可能无关。
由于B的二值离散约束, 上述目标转化为对称离散哈希分解问题[9], 其优化是个NP难题。为此, 本文借助Hadamard矩阵和已有的标签y直接生成离散哈希编码数据库B, 无需任何的迭代过程, 也无需调试任何的参数。
然后将原始ECG样本进行核化处理, 将其映射至再生核希尔伯特空间, 从而提升模型的非线性能力, 本文采用高斯核函数对样本进行非线性核化处理:
| $ \begin{aligned} \varphi\left(x_{i}\right)=&\left[\exp \left(-\frac{\left\|x_{i}-a_{1}\right\|_{2}^{2}}{\sigma^{2}}\right), \cdots, \right.\\ &\left.\exp \left(-\frac{\left\|x_{i}-a_{p}\right\|_{2}^{2}}{\sigma^{2}}\right)\right] \end{aligned} $ | (3) |
其中[a1, ⋯, ap] 表示从m个原始样本中随机选取的p(p < m) 个样本锚点;σ∈(0, 1) 为高斯参数。最后将核化后的数据通过学习的哈希函数映射到离散哈希编码库上, 以达到原始数据与哈希表示的相互匹配。
具体算法流程为:
1) 输入ECG信号标签y=(y1, ⋯, yn)T∈Nn;
2) 预设哈希码长度为k;
3) 根据公式(1)生成语义相似图S;
4) 根据公式(3)非线性核化处理ECG信号;
5) 随机生成矩阵H=Hadamard(k);
6) 利用信号标签y排列Hadamard矩阵H;
7) 生成哈希编码库B=H(y, : )。
生成哈希库之后, 我们还需要设计一个哈希函数f建立原始心电信号数据的再生核希尔伯特空间K={φ(X)|φ(X)∈Rn×p} 与潜在的海明空间H={B|B∈Rn×k} 的映射关系, 也为样本外数据提供可用的哈希函数。常用的哈希函数一般可以分为三类: 线性哈希函数、非线性哈希函数和深度哈希函数。限于篇幅原因, 本文只采用前两种哈希函数。
1) 线性哈希函数: 假设P∈Rp×k为一个线嵌入, 则线性分类器可以通过最小化下列损失构建:
| $ {{f}_{linear}}(P)=\|B-\varphi (X)P\|_{F}^{2}+\lambda \|P\|_{F}^{2} $ | (4) |
其中λ>0是防止过学习的正则化参数。利用最小二乘, 公式4的封闭解可表示为:
| $ P={{\left( {{\left[ \varphi \left( X \right) \right]}^{T}}\varphi \left( X \right)+\lambda I \right)}^{-1}}{{\left[ \varphi \left( X \right) \right]}^{T}}B $ | (5) |
对于任何一个查询样本xq, 其哈希编码可以由h(xq)=sign(PTφ(xq)) 生成。
2) 非线性哈希函数: 本文采用逻辑回归(logistic regression)函数作为非线性分类器, 采用一码一码的学习策略, 也就是学习k个分类器, 一个分类器对应一码, 从而生成查询样本xq哈希编码。针对第J个编码J=W*j, 可以通过最小化下列损失得到:
| $ {{f}_{lr}}(J)=\sum\limits_{i=1}^{n}{\log }\left( 1+\exp \left( -{{B}_{ij}}\varphi {{\left( {{x}_{i}} \right)}^{T}}J \right) \right)+\gamma \|J\|_{F}^{2} $ | (6) |
其中γ是防止过学习正则化参数。样本外数据xq利用哈希函数h(xq)=sign(WTφ(xq)) 即可生成哈希编码。
2.3 算法有效性验证为验证算法的有效性, 本文在国际公共心律失常数据集MIT-BIH上进行实验测试[10]。MIT-BIH数据集中主要包含四类心电图信号, N(正常博动信号), L(左束支传导阻滞), R(右束支传导阻滞)和V(室性早搏)。之前的ECG检测方法大都按照信号的采集和预处理、ECG信号的波形分析与多域特征提取、模型训练与预测等步骤[11]进行, 比如基于前馈神经网络(feedforward neural network, FNN)的ECG检测方法[12], 基于支持向量机(support vector machines, SVM)SVM的检测算法[13]或基于K最近邻(K-nearest neighbor, KNN)的ECG检测方法, 但这些方法能检测分类的心电图类型有限并且在实际应用中检测性能相对较低。卷积神经网络(convolutional neural networks, CNN)相较于前述方法, 性能上有很大的提高[14]。
本文在MIT-BIH数据集中随机选取8 000个样本用于训练, 2 000个样本进行测试, 两类哈希函数的正则化参数统一设置为0.1。一般的, 哈希编码越长, 准确率越高, 为了公平起见, 将哈希编码长度k确定为16。本文CNN算法和SSDH算法对上述N、L、R、V四类心电图信号识别准确率结果如表 1所示。
| 表 1 CNN与SSDH算法的准确率比较 |
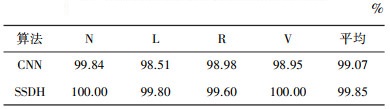 |
实验结果表明, SSDH算法识别的准确率达到了99.85%, 训练时间仅仅需要2 s, 相比于深度CNN测试结果的99.07%提高了接近0.8%, 训练耗时也远低于7层CNN算法的2 min训练时长。
图 3给出算法在哈希码长为16 bits时的准确率和召回率曲线图;图 4给出当训练集上哈希码长为16时, ECG哈希表示与哈希编码库的相似程度;图 5给出测试集上原始信号和提取的哈希表示的概率分布情况。简言之, SSDH算法在精度、查全率和计算时间方面优于传统方法。
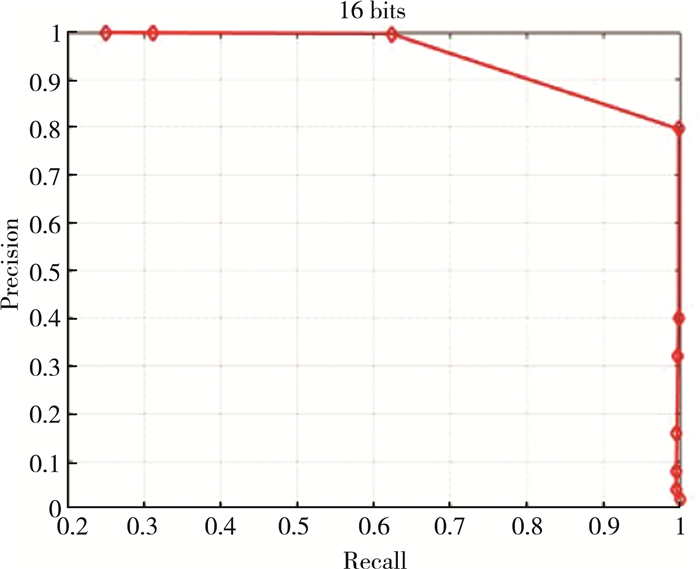 |
| 图 3 快速的SSDH算法的PR曲线图 |
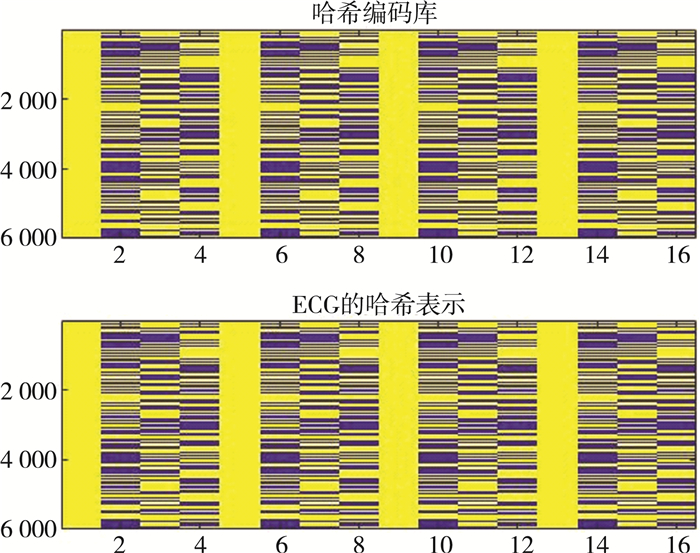 |
| 图 4 ECG哈希表示与哈希编码库的相似对比 |
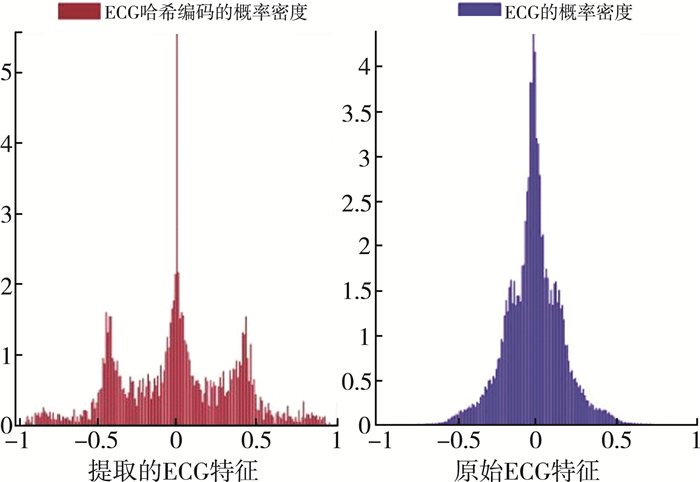 |
| 图 5 ECG哈希表示与原始信号的概率分布对比 |
2.4 算法创新点
本文创新性地提出一种高效离散语义对称分解哈希算法, 快速实施ECG信号的检测并且提高检索的正确率。把任意长度的ECG数据输入通过哈希算法紧致的二进制哈希表示, 在海明空间内实现信号的检测与识别, 既可以降低存储空间又可以提升检测的平均精度和最高精度。亮点在于该离散哈希算法不需要交替优化算法, 不需要迭代, 不依赖于初始值。
3 技术应用经过多年的发展, 心电图技术虽临床应用普遍, 但由于心电信号本身的复杂性和变异性, 传统心电图分析技术存在一定局限性, 无法做到自动、快速、准确地分析, 必须依靠专业医生进行分析解读, 而大部分医疗机构, 特别是基层医院, 专业心电图医师资源匮乏, 使得心电图检查疾病的应用效果受到局限, 大量基层心血管疾病患者无法获得及时、准确的诊断和防控治疗。近些年来, 以CT、MRI以及PET为代表的医学影像技术飞速发展, 医学影像已成为临床精确诊疗的必需手段。随着人工智能的逐渐普及, 心电自动诊断的重要性亦逐渐凸显[15]。心电自动诊断不但可以提供辅助诊断信息, 也可以24 h实时监控, 这对于移动医疗、远程诊断都大有裨益。
本文主要利用语义对称分解哈希的方法提高ECG检索的正确率和速度, 适用于智能医疗领域中通过高效准确的ECG信息检测来预测、识别和精确诊疗心血管异常现象的情况, 预计该技术将在如下领域得到广泛应用:
1) 大量基层医院、个体诊所、养老机构等缺乏专业的心电医生, 此产品的应用将实现患者在这些机构的属地化、快速化心电分析诊断。
2) 减轻大型医院专业心电医生的工作量。既提高工作效率, 又提升诊断水平。
3) 心电监测进入家庭, 使得患者在家中像监测血压、血糖一样方便快捷地进行静态和动态的心电监控。
4) 将可穿戴设备的心电分析和诊断水平提升至专业医生水平, 强化穿戴设备(手表、手环等)的功能。
4 结论本文提出了一种基于语义对称分解哈希(SSDH)的监督学习方法, 根据ECG各个波段具有的不同特点, 来实施ECG检索与信号匹配。SSDH算法对数据标签生成的语义相似进行离散对称哈希分解, 从而生成哈希编码库, 最后学习哈希函数建立海明空间与原始数据核化空间的映射关系。针对离散优化需要通过交替优化或离散循环坐标下降等方法实施混合整数规划问题, SSDH算法借助语义标签排列Hadamard矩阵, 无需迭代和任何参数的调试即可快速地生成哈希编码库。在已有的国际公共数据集MIT-BIH上进行程序设计及仿真测试, 结果表明SSDH算法在极少的训练时间下即可完成对大量ECG信号进行快速分类的任务, 识别精度也超过CNN深度模型。
| [1] |
王莉莎. 基于张量分析的心律失常ECG信号特征研究[D]. 北京: 北京理工大学, 2017.
|
| [2] |
瞿文凤. 基于深度学习的心电信号分类识别方法研究[D]. 成都: 西华大学, 2020.
|
| [3] |
张宇微. 面向心血管疾病识别的心电信号分类研究[D]. 济南: 济南大学, 2019.
|
| [4] |
孙梦莉. 基于深度迁移学习的心电信号分类算法研究[D]. 大连: 大连海事大学, 2020.
|
| [5] |
NAHIAN IBN HASAN, ARNAB BHATTACHARJEE. Deep learning approach to cardiovascular disease classification employing modified ECG signal from empirical mode decomposition[J]. Biomedical Signal Processing and Control, 2019, 52: 128-140. DOI:10.1016/j.bspc.2019.04.005 |
| [6] |
周志波. 基于特征融合CNN模型的ECG信号识别方法研究[J]. 软件导刊, 2020, 19(11): 46-49. |
| [7] |
刘志锋. 分布式快速监督离散哈希算法研究[D]. 重庆: 西南大学, 2020.
|
| [8] |
KOUTAKI GOU, SHIRAI KEIICHIRO, AMBAI MITSURU. Hadamard coding for supervised discrete hashing[J]. IEEE Transactions on Image Processing, 2018, 27(11): 5378-5492. DOI:10.1109/TIP.2018.2855427 |
| [9] |
贾佳. 基于离散监督哈希的图片检索算法研究[D]. 西安: 西安电子科技大学, 2019.
|
| [10] |
朱振宇. 心电信号数据提取算法的设计与实现[D]. 北京: 北京交通大学, 2010.
|
| [11] |
艾嘶吗. 基于心电图信号特征的心率异常检测[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [12] |
王弢, 侯建军, 吴北玲. FNN在心率失常判别中的研究[J]. 北方交通大学学报, 2002, 26(6): 90-93. |
| [13] |
孙波, 杨磊, 郭秀梅, 等. 基于CNN和SVM混合模型的心电信号识别方法[J]. 山东农业大学学报(自然科学版), 2020, 51(2): 283-288. |
| [14] |
史健婷, 吴荣强, 张海楠, 等. 基于卷积神经网络的心电信号分类实现[J]. 信息系统工程, 2020(2): 122-123. |
| [15] |
王莹莹, 薛超, 殷兆芳, 等. 智能诊断在心电图诊断的发展历程及应用进展[J]. 心血管康复医学杂志, 2019, 28(4): 502-505. DOI:10.3969/j.issn.1008-0074.2019.04.28 |
 2021, Vol. 35
2021, Vol. 35


