| 通信系统中8QAM调制下误码率与信噪比关系 |
通信系统中, 为了使数字信号在带通信道中传输, 需要用数字信号对载波进行调制, 将调制的信号传送到更高的频段[1-2]。正交振幅调制(Quadrature Amplitude Modulation, QAM)和多进制相移键控(M-ary Phase Shift Keying, MPSK)在数字调制技术中具有广泛的应用, 但由于QAM的抗干扰性要优于MPSK[3], 因此QAM的利用率更高, 常被应用于普通数字电视以及电视互动业务中[4]。
现代数字传输系统是对二进制序列进行编码传输的系统, 其中1个二进制的0或1称为1个比特(bit)。任何信息都可以数字化为一列二进制比特序列, 经过编码并调制为某个“载体信号”, 再通过信道传输到目的地。在光纤通信中, 信道为光纤, 信息的载体为光波。通常把信号矢量端点的分布图称为“星座图”, 图上的点称为“星座点”[1]。本文主要研究8QAM的调制格式, 其星座图如图 1所示[1]。
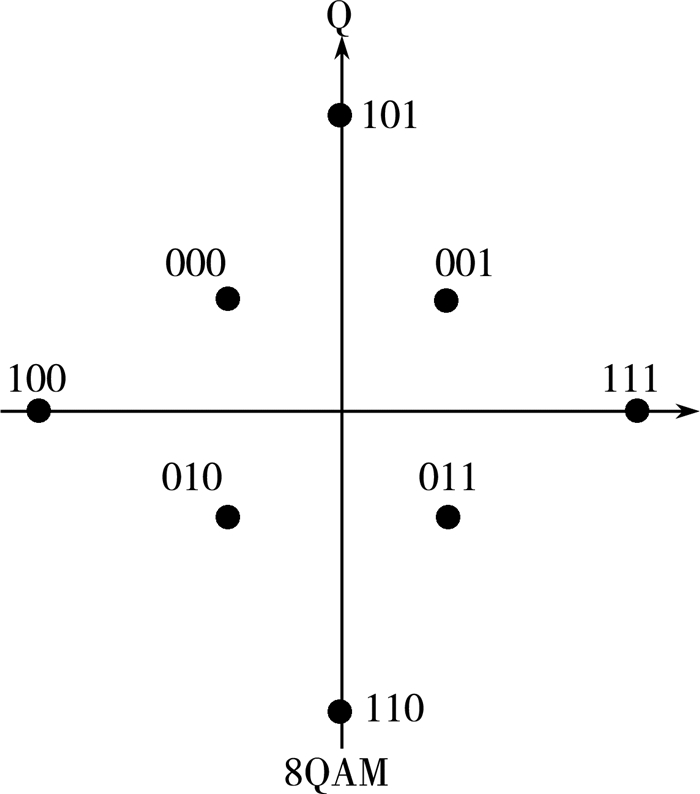 |
| 图 1 8QAM调制格式星座图 |
在恒参信道条件下[5], 信号的传送会受到噪声的干扰, 可能发生错误导致误码。信号经过信道叠加噪声和接收机处理后, 接收端的星座图不再是理想的8个点, 而是会出现扩散, 其中噪声通常服从均值为0的正态分布。当接收机收到1个符号时, 就将发送的符号判定为离该符号最近的星座点。
1 误码率与信噪比的关系误码率(Bit Error Ratio, BER)定义为错误的比特数占总传输比特数的比例。信噪比(Signal to Noise Ratio, SNR)定义为一个电子设备或者电子系统中信号与噪声功率的比例。研究BER与SNR的关系, 即计算比特出错的概率。本文由噪声[5]的定义以及噪声与星座点的关系, 得到了调制后星座点附近比特的概率分布。比特在经过噪声干扰后的横坐标(x)与纵坐标(y)相互独立, 故可以知道二维随机变量(x, y)的联合概率密度。求解过程可以归纳为:
1) 求出比特正确判定为相应星座点的概率。
2) 计算误码率BER=1-正确概率。
如图 1所示, 我们根据概率分布情况, 将8QAM调制格式的八个点归为两类:一类是不在坐标轴上的点{000, 001, 010, 011};另一类是在坐标轴上的点{101, 111, 110, 100}。在以下的计算过程当中, 对于第一类点, 记正确判定的概率为φ1; 对于另一类点, 记正确判定的概率为φ2。
设001的星座坐标为(g, g), 则101的星座坐标为((0, (1+
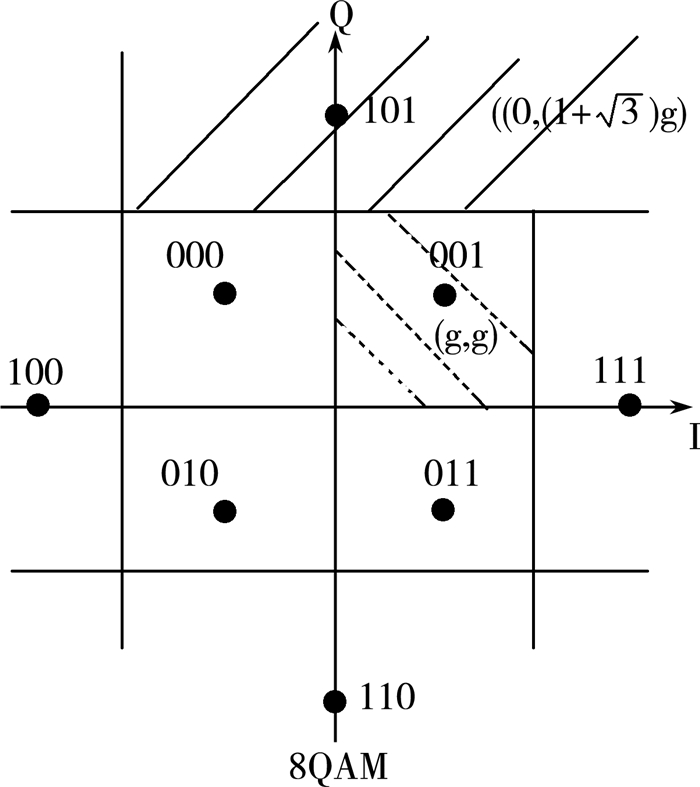 |
| 图 2 判定区域图 |
计算在001点的正确概率φ1。由于x1与y1相互独立, 且(x1, y1)服从二维正态分布[6], 即:
| $ \begin{array}{l} ({x_1}, {y_1}) \sim N(g, g, {\sigma ^2}, {\sigma ^2})\\ {\varphi _1} = \int_0^{\left( {1 + \frac{{\sqrt 3 }}{2}} \right)g} {} \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{({x_1} - g)}^2}}}{{2{\sigma ^2}}}}}d{x_1}\int_0^{\left( {1 + \frac{{\sqrt 3 }}{2}} \right)g} {} \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{({y_1} - g)}^2}}}{{2{\sigma ^2}}}}}d{y_1} \end{array} $ | (1) |
同理, 计算在101点的正确概率φ2。由于x2与y2相互独立, 且(x2, y2)服从二维正态分布[7-8], 即:
| $ \begin{array}{l} ({x_2},{y_2}) \sim N(0,\left( {1 + 3} \right)g,{\sigma ^2},{\sigma ^2})\\ {\varphi _2} = \int_{\left( { - 1 - \frac{{\sqrt 3 }}{2}} \right)g}^{ + \infty } {} \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{x_2}^2}}{{2{\sigma ^2}}}}}d{x_2}\int_{\left( {1 + \frac{{\sqrt 3 }}{2}} \right)g}^{ + \infty } {} \\ \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{({y_2} - \left( {1 + 3} \right)g)}^2}}}{{2{\sigma ^2}}}}}d{y_2} \end{array} $ | (2) |
信号平均功率为[5]:
| $ {p_s} = \frac{{{A^2}}}{M}\sum\limits_{n = 1}^M {} ({c_n}^2 + {d_n}^2) $ | (3) |
其中(cn, dn)为每个星座点的坐标, M为星座点的个数, A为振幅, 2A为信号点之间的最小距离。本问题中A=g, 从而可计算得:
| $ {p_s} = \left( {3 + 3} \right){g^4} $ | (4) |
噪声平均功率为:
| $ {p_n} = {\sigma ^2} $ |
| $ SNR = \frac{{{p_s}}}{{{p_n}}} = \frac{{\left( {3 + 3} \right){g^4}}}{{{\sigma ^2}}} $ | (5) |
又由于:
| $ BER = 1 - \frac{1}{2}({\varphi _1} + {\varphi _2}) $ | (6) |
故由式(1)~(6)可以得到误码率与信噪比关系如下:
| $ \begin{array}{l} BER = 1 - \frac{1}{2}\left[ {1 - erfc\left( {\sqrt {\frac{{SNR}}{{6 + 2\sqrt 3 }}} } \right) - } \right.\\ \frac{1}{2}erfc\left( {\sqrt {\frac{{3SNR}}{{3 + \sqrt 3 }}} } \right){\left. {} \right]^2} - \frac{1}{2}\left[ {1 - \frac{1}{2}erfc\left( {1 + \frac{{\sqrt 3 }}{2}} \right)} \right.\\ \left. {\left. {\sqrt {\frac{{SNR}}{{6 + 2\sqrt 3 }}} } \right]} \right)\left[ {1 - \frac{1}{2}erfc\left( {\frac{1}{2}\sqrt {\frac{{3SNR}}{{6 + 2\sqrt 3 }}} } \right)} \right] \end{array} $ |
其中:
本文基于8QAM调制格式的基本原理, 借助于概率统计学的知识, 详细计算得到了8QAM调制格式下误码率与信噪比的关系表达式。该研究不仅有利于现代通信理论的发展, 更有利于现实生活中通信系统的完善。
| [1] |
曹志刚, 钱亚生. 现代通信原理. [M]. 北京: 清华大学出版社, 2008.
|
| [2] |
涂翔宇, 汤定藩, 张洪珊. QAM原理及其在HFC系统中的应用[J]. 中国有线电视, 2002, 5: 11-14. |
| [3] |
张辉, 曹丽娜. 通信原理. [M]. 北京: 科学出版社, 2007.
|
| [4] |
宫丰奎, 李兵兵, 张乔乔. 全数字QAM解调系统的设计与仿真[J]. 电视技术, 2004(3): 57-59. DOI:10.3969/j.issn.1002-8692.2004.03.018 |
| [5] |
茆诗松, 程依明, 濮晓龙. 概率论与数理统计教程. [M]. 北京: 高等教育出版社, 2011.
|
| [6] |
王琪. 通信原理. 第2版[M]. 北京: 电子工业出版社, 2018.
|
| [7] |
王福昌, 屈代明. 通信原理. 第2版[M]. 北京: 清华大学出版社, 2015.
|
| [8] |
袁国良. 光纤通信原理. 第2版[M]. 北京: 清华大学出版社, 2012.
|
 2019, Vol. 33
2019, Vol. 33


