| 基于改进BINN算法的波浪滑翔机航迹规划研究 |
新世纪以来, 随着各个国家城市化和工业化的迅速发展, 各种陆地资源的消耗巨大, 各个国家逐步放眼于海洋资源的开发, 致力于推广沿岸经济。而随着无人技术的出现和大数据、人工智能等的不断发展, 船舶的自动化程度越来越重要, 逐渐成为未来船艇发展的重点方向, 而基于海洋观测的大尺度长时序以及环境的恶劣程度等问题, 波浪滑翔机的研究便成为海洋观测方面的一个重要的课题[1]。
在波浪滑翔机的发展过程中, 其航迹规划问题一直是一个亟待解决的核心问题, 本课题将利用生物激励神经网络(BINN)算法研究波浪滑翔机的航迹规划问题, 即在一个已知或未知的环境中要求波浪滑翔机根据自身传感器所接受到的关于周围环境的信息, 控制自身的状态(速度、方向等)寻找到一条最优或较优的安全航行轨迹[2-4]。
1 运动空间数学建模研究波浪滑翔机的航迹规划之前, 首先应对波浪滑翔机的运动空间进行环境建模, 为了提高航行轨迹规划算法在大范围的环境内的航迹规划效率, 这里在对波浪滑翔机的运动空间进行环境建模时采用四叉树(Q-tree)的空间分割方法, 该方法是树形数据结构, 在保持环境信息不丢失的前提下可以高效的对环境信息进行压缩, 降低航迹规划过程中的运算规模, 有效提高航迹规划效率[5]。其分割规则如下:
(1) 将波浪滑翔机的二维工作区域作为根节点, 编码为0。
(2) 将根节点沿东西方向和南北方向进行四等分, 每个节点作为根节点的子区域, 并且将这四个子节点依据其所在方位, 由西向东, 由北向南的顺序, 在根节点的编码之后编码为1~4, 即编码为01~04。
(3) 由步骤2所形成的四个子区域中, 如果该子区域中全为障碍物, 则该子区域称为障碍子节点;如果该子区域中没有障碍物, 则称该区域为自由子节点;如果该子区域既有障碍物又有可航行区域, 则该子区域称为混合节点。
(4) 混合节点存在时, 则对该节点按照步骤2与步骤3的划分规则继续分解, 在划分后的节点没有混合节点后停止划分[6]。
利用上述对波浪滑翔机运行空间的分割规则, 图 1、图 2给出了利用该规则进行分解与命名的实例, 其中白色方框与圆圈代表自由子节点, 黑色方框与圆圈代表障碍子节点, 灰色圆圈代表混合节点。
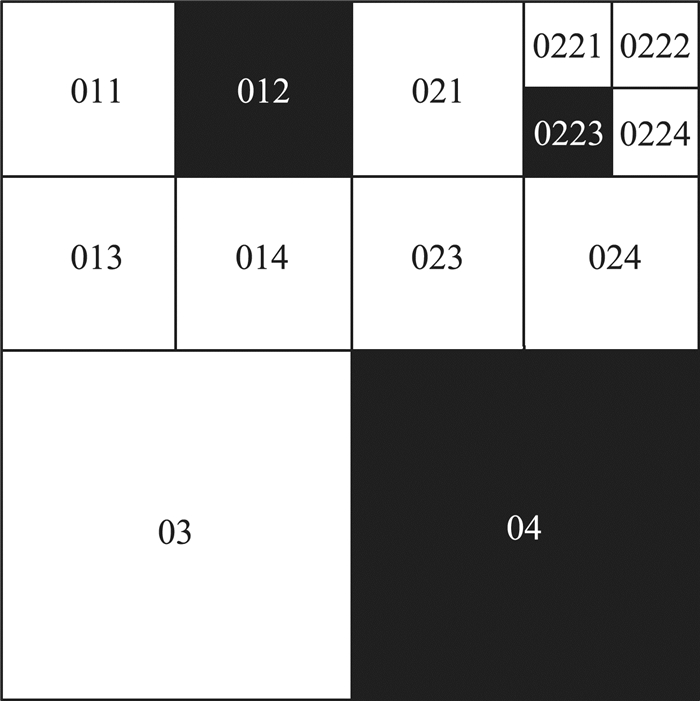 |
| 图 1 四叉树分解实例 |
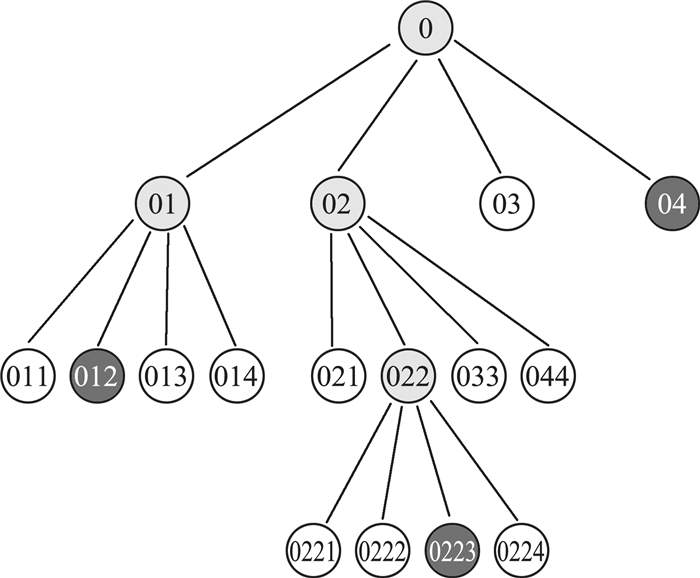 |
| 图 2 四叉树分解命名规则 |
由图 1可知, 如果在给出的环境中利用栅格环境建模, 则其需要的环境栅格数为64, 而这里利用四叉树法进行环境建模仅仅使用了13个栅格, 则波浪滑翔机在进行航迹规划时, 需要计算的栅格数减少了51个, 由此实例可知, 四叉树法大大降低了需要运算的栅格的数量, 提高了波浪滑翔机航迹规划的效率。
2 改进BINN航迹规划算法 2.1 传统算法Yang等在总结了细胞膜电路特性模型之后, 将该模型应用于路径规划中, 由此提出了生物激励神经网络(BINN)算法[7-8]。与其他算法相比, 该算法不需要预先扫描环境, 无需预先学习, 计算机存储容量小, 响应速度快, 低计算复杂度[9]。在该算法中, 波浪滑翔机的航行环境由栅格组成的神经元表示, 每个神经元栅格都对应一个动态活性值, 动态活性值初始状态为0, 而活性值大小可以由分流方程来计算得出, 分流方程如式(1)所示:
| $ \frac{\mathrm{d} x_i}{\mathrm{~d} t}=-A x_i+\left(B-x_i\right) S_E-\left(D+x_i\right) S_I, $ | (1) |
式中, 用xi表示第i个邻接神经元的活性值大小;常数A代表活性值的衰弱速率;常数B和D分别是邻接神经元活性值的上下界;SE和SI分别表示兴奋与抑制性激励;其定义如式(2)、式(3)所示:
| $ S_E=\left[I_i\right]^{+}+\sum\limits_{j=1}^k w_{i j}\left[x_j\right]^{+} $ | (2) |
| $ S_I=\left[I_i\right]^{-}。$ | (3) |
Ii是第i个邻接神经元外部输入激励, 目标点和障碍物的外部输入激励分别为正负E, 其绝对值是一个远大于B的常数[10-11], [a]+=max{a, 0}, [a]-=max{-a, 0}, k为邻接神经元的数量, wij=f(dij)为连接权重, dij为当前神经元与第j个邻接神经元的欧氏距离, 并且当前神经元与邻接神经元只在半径为r0的小范围内有局部连接, 若超出此范围, 即a≥r0时, 则f(a)=0, 当0 < a < r0时, f(a)=u/a, u是一个正常数。利用该算法生成具体路径的表达式为[12]:
| $ p_n \Leftarrow x_{p_n}=\max \left\{x_j, j=1, 2, \cdots, k\right\}, $ | (4) |
式中, k为第pn个神经元的邻接神经元的数量, 波浪滑翔机从起点开始, 判断当前邻域内每个神经元的活性值, 选择相邻神经元活性值最大的位置单元作为下一个位置, 波浪滑翔机从当前位置到达下一个位置后, 将下一个位置作为新的当前位置, 然后以同样的方法到达下一个位置, 以此类推, 直到到达目标点。
2.2 路径修正策略分析因为波浪滑翔机在实际航行过程中, 转向能力较差, 而此算法在轨迹规划过程中可能出现方向突变的问题, 基于此, 在路径栅格生成过程中, 将下一位置栅格的方向考虑进来, 则其具体路径为:
| $ p_n \Leftarrow x_{p_n}=\max \left\{x_j+c_1 T_j, j=1, 2, \cdots, k\right\}, $ | (5) |
式中, c1是一个正常数, Tj是一个关于波浪滑翔机上一个位置U、当前位置V和可能的下一个位置W的函数, 函数定义为Tj=λ/Δθ, 其中Δθ∈[0, π], 表示当前时刻的艏向角与下一时刻的艏向角之间的角度。
| $ {\mathit{\Delta }}\theta=\left|\theta_1-\theta_2\right|=|| \arctan \left(y_c-y_b, x_c-x_b\right)|-| \arctan \left(y_b-y_a, x_b-x_a\right)|| 。$ | (6) |
因为波浪滑翔机实际航行环境可能比较复杂, 在路径规划过程中可能会出现陷入死区的情况, 即邻接神经元的活性值相同的情况, 为有效地避开障碍物并优化路径的平滑度, 解决规划过程中的死区问题, 将波浪滑翔机航迹规划过程中与目标点的距离影响考虑进来[13], 实际实现分析情况如图 3所示。
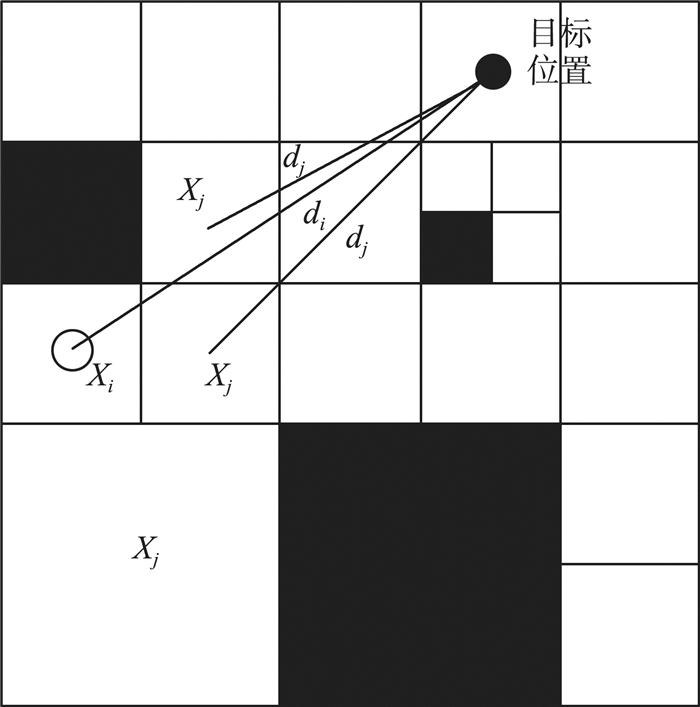 |
| 图 3 航迹规划距离影响机制分析 |
如图 3所示, 波浪滑翔机当前位置所在单元的活性值为Xi, 其到目标点的距离为di;假定当前位置单元的邻接神经元的活性值为Xj, 其到目标点的距离为dj;为了平滑波浪滑翔机的航行轨迹, 解决死区问题[14], 采用如下的航迹修正策略:
| $ p_n \Leftarrow x_{p_n}=\max \left\{x_j+c_2 \frac{d_i}{d_j}, j=1, 2, \cdots, k\right\}, $ | (7) |
式中, c2为一个常数;c2(di/dj)是航迹修正率, 该参数的引入加强了外部的输入激励, 一定程度上改善了死区问题, 使得生成的路径更加理想。
2.3 航迹规划具体步骤全局航迹规划算法步骤流程图如图 4所示。
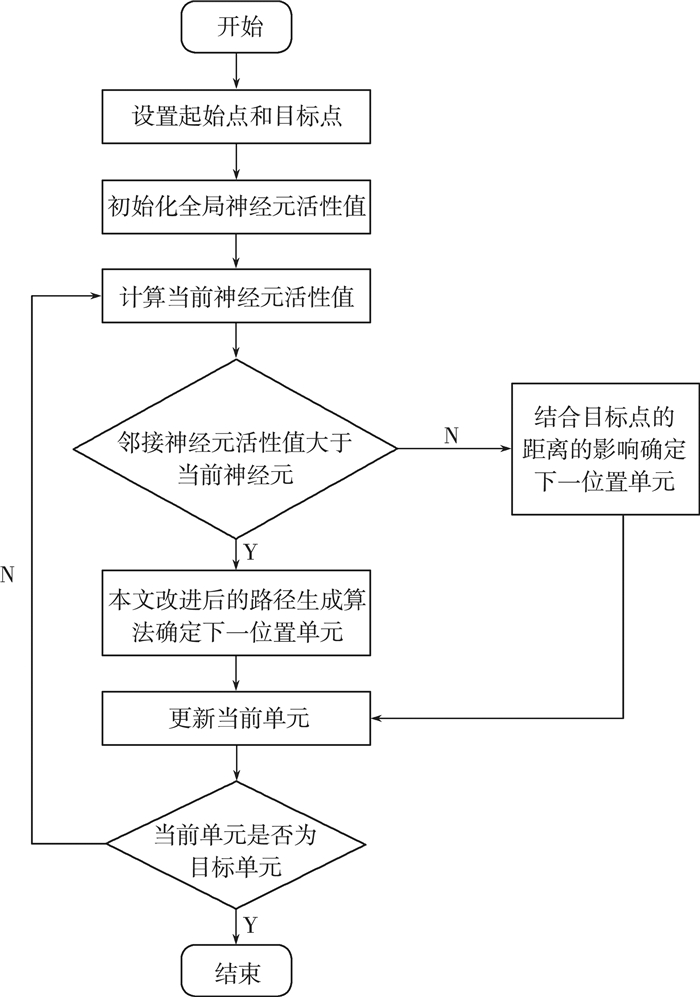 |
| 图 4 算法步骤流程图 |
(1) 设置起始点位置和目标点位置;
(2) 对全局神经元活性值以及各参数进行初始化;
(3) 在神经元活性值作用到整个规划区域之后, 根据活性值计算公式, 计算得出当前神经元以及邻接自由神经元的活性值, 并判断邻接神经元是否大于当前神经元活性值;
(4) 如果邻接神经元大于当前神经元活性值, 则波浪滑翔机移动到此位置单元, 如果出现陷入死区问题, 即邻接神经元小于等于当前神经元活性值情况, 则结合目标点的距离影响确定下一位置单元;
(5) 判断当前位置是否为目标点, 若没有到达目标点则跳转到步骤(3)、(4)继续执行, 否则结束。
3 实验仿真本文运用MATLAB R2020b进行代码编写以及仿真运行。为了验证改进型BINN算法对波浪滑翔机的适用性, 对比传统BINN算法, 将其应用于复杂海域内进行仿真。假定在该复杂海域内随机产生不规则障碍物, 并在该海域内应用四叉树建立环境模型后进行仿真研究。仿真研究中, 波浪滑翔机的起始点与目标点是给定的, 分别用圆圈与五角星表示, 不可通行区域用灰色表示, 白色代表可通行区域, 随机地图生成后, 在此地图上建立四叉树模型, 波浪滑翔机走过的栅格用蓝色表示, 设定环境地图大小为1 024×1 024, 当波浪滑翔机到达目标点时, 认定为任务完成, 航迹规划任务停止执行, 仿真实验对比图如图 5、图 6所示。
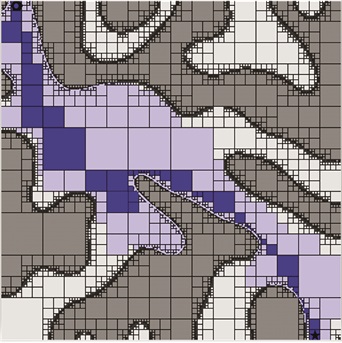 |
| 图 5 传统BINN算法仿真 |
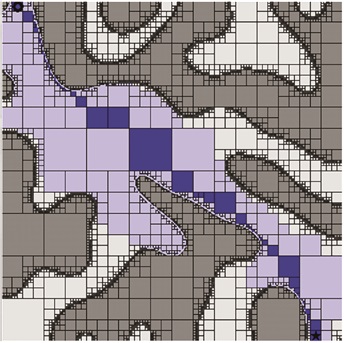 |
| 图 6 改进BINN算法仿真 |
仿真结果表明, 与传统BINN算法相比, 利用改进后的BINN算法生成的路径大大缩短, 对于复杂不规则的地形, 波浪滑翔机可以在保证安全距离的前提下有效避开障碍物, 此外, 通过改进BINN算法与四叉树环境建模相结合, 在大范围的海洋环境进行航迹规划时, 四叉树法环境建模对环境信息进行了高效的压缩, 大大提高了航迹规划过程中的效率与灵活性, 所以改进方法是有效可行的。
4 总结本文针对波浪滑翔机的航迹规划问题, 采用了改进BINN算法与四叉树法相结合的航迹规划方法, 与传统BINN算法相比, 改进的BINN算法规划的航迹大大缩短, 采用四叉树法对环境进行建模, 不仅完整地保留了环境信息, 同时也对环境信息进行了压缩, 从而保证了波浪滑翔机在海洋环境这种大范围区域内进行航迹规划的效率。最后, 仿真实验验证了改进方法的有效性。
| [1] |
毛宇峰. 水下机器人系统体系结构及避障控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [2] |
姜月秋, 李紫嫣, 关启学, 等. 基于改进A*算法的无人机路径规划研究[J]. 兵器装备工程学报, 2020, 41(9): 160-164. |
| [3] |
燕翔, 高军伟, 官晟. 基于模式转变蚁群算法的波浪滑翔机路径规划[J]. 计算机工程与应用, 2019, 55(9): 100-106. |
| [4] |
陈茜. 基于遗传—改进蚁群融合算法的波浪滑翔机路径规划研究[D]. 青岛: 青岛大学, 2020.
|
| [5] |
张阳伟, 乔越, 李成凤. 基于四叉树栅格环境的变步长双向A*算法[J]. 控制工程, 2021, 28(10): 1960-1966. |
| [6] |
赵百轶, 张利军, 贾鹤鸣. 基于四叉树和改进蚁群算法的全局路径规划[J]. 应用科技, 2011, 38(10): 23-28. |
| [7] |
YANG S X, MENG M. An efficient neural network approach to dynamic robot motion planning[J]. IEEE Transactions on Neural Networks, 2000, 13(2): 143-148. DOI:10.1016/S0893-6080(99)00103-3 |
| [8] |
YANG S X, MENG M. Neural network approaches to dynamic collision-free trajectory generation[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2001, 31(3): 302-318. DOI:10.1109/3477.931512 |
| [9] |
吕战永, 曹江涛. 自反馈生物激励神经网络机器人路径规划[J]. 计算机工程与应用, 2014, 50(16): 255-258. DOI:10.3778/j.issn.1002-8331.1208-0394 |
| [10] |
YANG S X, MENG M. Real-time collision-free motion planning of a mobile robot using a neural dynamics-based approach[J]. IEEE Transactions on Neural Networks, 2003, 14(6): 1541-1552. DOI:10.1109/TNN.2003.820618 |
| [11] |
LUO C, YANG S X. A bioinspired neural network for real-time concurrent map building and complete coverage robot navigation in unknown environments[J]. IEEE Transactions on Neural Networks, 2008, 19(7): 1279-1298. DOI:10.1109/TNN.2008.2000394 |
| [12] |
YANG S X, ZHU A, YUAN G, et al. A bioinspired neurodynamics-based approach to tracking cntrol of mobile robots[J]. IEEE Transactions on Industrial Electronics, 2012, 59(8): 3211-3220. DOI:10.1109/TIE.2011.2130491 |
| [13] |
张秦, 段中兴. 基于改进的生物激励神经网络机器人路径规划算法[J]. 计算机测量与控制, 2020, 28(7): 204-209. |
| [14] |
王耀南, 潘琪, 陈彦杰. 改进型生物激励神经网络的路径规划方法[J]. 控制工程, 2018, 25(4): 541-548. |
 2022, Vol. 36
2022, Vol. 36


