| 等加速度控制AMT软起动带式输送机的仿真研究 |
2. 山东大学 机械工程学院,济南 250061
2. School of Mechanical Engineering, Shandong University, Jinan 250061, China
现有带式输送机软起动设备有变频调速设备、交流电机软起动设备、调速型液力偶合器、CST可控起动传输设备等[1-2]。这些软起动设备大多成本较高, 且维护费用也较高, 在应用中有各自的不足。
国内外学者对带式输送机的软起动研究主要集中在如何减小输送带的张力和张力的变化[3-7]。输送带张力的大小与其加速度有关, 因而带式输送机起动时输送带的加速度控制尤为重要。国外广泛采用Harrsion提出的正弦形加速度控制曲线和Nordell提出的三角形加速度控制曲线。国内宋伟刚教授在总结前人的研究基础上在其专著中提出了四种理想起动理念:1)等加速度起动;2)梯形加速度起动;3)组合摆线速度起动;4)组合抛物线速度起动。这几种方式实际应用中都需要电机的调速, 使得系统变得复杂, 从而提高了成本。
AMT(Automated Mechanical Transmission)在汽车上已有了成熟的应用, 且造价低、维护简单。考虑到带式输送机起动与车辆起步之间的相似性, 本文提出以三相异步电机为动力、以AMT作为新的软起动装置, 利用逐级换挡实现带式输送机的软起动。目前AMT技术可满足300 kW以下重型车辆的使用要求[8], 本方案主要应用于300 kW以下中小型带式输送机上。
文中首先分析了AMT软起动带式输送机的工作原理, 然后分析了离合器控制扭矩与输送带加速度的关系, 之后提出了等加速度控制输送带的AMT软起动控制方法, 并在110 kW平运单点驱动带式输送机的基础上进行了AMT软起动带式输送机的建模, 最后进行了起步过程和换挡过程的仿真分析。
1 AMT的工作原理 1.1 车辆AMT的工作原理车辆AMT的基本原理可以简单地描述为:在固定轴式变速器的基础上加装自动换挡执行机构, 采用变速器控制单元控制执行机构, 根据驾驶员的换挡要求, 自动完成离合器的分离、接合和变速器的换挡操作。
AMT控制规律的制定以熟练驾驶员的最佳驾驶方法为依据, 包括起步模式、换挡规律、离合器接合规律等。汽车的换挡规律主要有三种类型:单参数换挡规律、两参数换挡规律和三参数换挡规律。目前车辆上多采用两参数换挡规律, 控制参数多为油门和车速[9-11]。
AMT的核心问题是离合器的最佳接合规律。文献中多将离合器的接合过程分为:克服自由行程阶段、克服阻力阶段、车辆加速阶段和同步无滑磨四个阶段[12]。根据这四个阶段的特点制定离合器的接合规律, 提高起步品质和换挡品质。
1.2 带式输送机AMT的工作原理文中采用三相异步电机作为动力源, 以AMT作为软起动装置, 逐步换挡实现带式输送机的软起动。整个系统组成和原理如图 1所示。
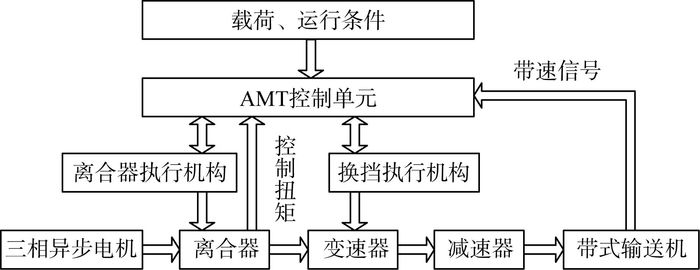 |
| 图 1 AMT软起动带式输送机的组成和原理 |
带式输送机的起动不像汽车需要驾驶员的干预和较高的换挡品质, 文中选择单参数控制规律, 控制参数为带速。各个挡位的目标带速由电机的额定转速及传动装置的传动比计算得到。
对离合器压紧力的控制可实现离合器传递扭矩的控制, 从而控制输送带的加速度。文中参考车辆离合器“快-慢-快”的接合规律, 减少起步冲击和换挡冲击。
2 离合器控制扭矩分析车辆上离合器传递扭矩主要由发动机的输出扭矩来决定, 发动机的扭矩又由油门来控制, 而带式输送机软起动系统中动力源为三相异步电动机, 三相异步电机的输出扭矩由后面带动的负载来决定。因此, AMT软起动系统的电机输出扭矩与离合器的控制扭矩有关。为了使输送机起动过程可控, 研究离合器控制扭矩与输送带的加速度的关系非常必要。
2.1 带式输送机运行阻力带式输送机运行阻力包括:主要阻力、附加阻力、提升阻力和特种阻力。由此, 带式输送机的运行阻力可用下式表示:
| $ {F_f} = {F_H} + {F_N} + {F_{St}} + {F_S} $ | (1) |
式中, Ff为运行阻力(N);FH为主要阻力(N);FN为附加阻力(N);FSt为提升阻力(N);FS为特种阻力(N)。
输送机的运行阻力矩为:
| $ {T_f} = {F_f} \cdot R $ | (2) |
等效到离合器从动轴上的等效阻力扭矩为
| $ {T_L} = \frac{{{T_f}}}{{{i_g} \cdot {i_0} \cdot \eta }} $ | (3) |
式中, R为驱动滚筒半径(m);ig为变速器传动比;i0为减速器传动比;η为传动效率。
2.2 离合器控制扭矩忽略不同挡位变速器输出轴转动惯量的差异(以变速器厂家提供的输出轴转动惯量为依据), 离合器控制扭矩与输送带的加速度关系为:
| $ {T_C} = {T_L} + \frac{{\left( {M \cdot {R^2} + {J_g} \cdot i_0^2 + {J_0} \cdot i_0^2 + {J_{cf}}} \right)}}{{R \cdot {i_g} \cdot {i_0} \cdot \eta }} \cdot \frac{{dv}}{{dt}} $ | (4) |
式中TC为离合器控制扭矩(N·m);M为带式输送机的等效运动质量(kg);Jg为变速器输出轴的转动惯量(kg·m2);J0为减速器输入轴的转动惯量(kg·m2);Jcf为离合器从动盘的转动惯量(kg·m2);v为带速(m/s)。
从式(4)中可以看出, 系统固有参数确定后, 离合器控制扭矩与输送带的加速度成线性关系。当负载和阻力扭矩确定后, 控制离合器的传递扭矩可实现对输送带的加速度控制。
3 等加速度控制AMT软起动带式输送机模型的建立为保证物料与输送带之间不打滑, 输送带的起动加速度一般控制在0.1~0.3 m/s2[5]。由于输送带起动加速度值的限制, 笔者提出等加速度控制AMT软起动带式输送机的方法, 控制输送带的加速度值为0.2 m/s2。
3.1 主要参数1) 三相异步电机Y315S-4:额定功率110 kW;额定转速1480 r/min, 最大扭矩系数2.2, 转子转动惯量3.11 kg·m2。
2) 变速器:某型AMT输出轴的转动惯量10 kg·m2, 最大输入扭矩1900 N·m。8个挡位的传动比分别为14.28、10.62、7.87、5.87、4.375、3.26、2.43、1.80。
3) 离合器:主动件转动惯量2.25 kg·m2, 从动件转动惯量0.135 kg·m2。
4) 减速器:传动比为10。
5) 输送机:运输量1600 t/h, 输送带型号ST1250, 弹性模量E=65σN=81250 kN/m[5], 阻尼系数η=0.1468E=11928 KPa·s[13], 倾角0°, 长度400 m, 带宽1.2 m, 单位长度质量26.64 kg/m;托辊直径133 mm, 槽角35°, 上托辊间距1.2 m, 下托辊间距3 m;驱动滚筒直径1 m、转动惯量262 kg·m2, 拉紧滚筒和尾部改向滚筒直径800 mm、转动惯量87 kg·m2, 90°改向滚筒直径630 mm、转动惯量38 kg·m2。
3.2 三相异步电机建模文献[14]给出了三相异步电机机械特性的实用表达式。从厂家产品目录中查到的有关参数可便于实用表达式建模。
建立三相异步电机电机转差率与电磁转矩之间的关系:
| $ s = \frac{{{n_1} - n}}{{{n_1}}} $ | (5) |
| $ {s_m} = {s_N}\left( {{\lambda _m} + \sqrt {\lambda _m^2 - 1} } \right) $ | (6) |
| $ T = \frac{{2{T_m}}}{{\frac{s}{{{s_m}}} + \frac{{{s_m}}}{s}}} $ | (7) |
式中, s为转差率;n1为同步转速(r/min);n为转子转速(r/min);sm为最大扭矩时的转差率;sN为额定扭矩时的转差率;λm为最大扭矩系数;T为三相异步电机的电磁转矩(N·m);Tm为三相异步电机最大扭矩(N·m)。
3.3 输送机建模输送带具有粘弹性特征, 使得建模变得复杂。文献中研究较多的是Maxwell模型(弹簧和阻尼器串联)和Kelvin模型(弹簧和阻尼器并联)[15-17]。文中采用Kelvin模型。
Kelvin模型的总应力与总应变的关系
| $ \sigma = E\varepsilon + \eta \frac{{d\varepsilon }}{{dt}} $ | (8) |
式中, σ为弹簧与阻尼器的总应力(Pa);ε为弹簧与阻尼器的总应变;E为弹簧的弹性模量(Pa);η为阻尼器的粘性系数(Pa·s)。
带式输送机拉紧装置可分为重锤式、固定式和自动拉紧装置。重锤式拉紧装置在输送机起动和停机时拉紧重锤的惯性力会影响张紧力的变化, 而自动拉紧装置的结构和控制又比较复杂, 为了便于建模, 本文选择固定拉紧方式。
张紧力是由驱动滚筒所传递的最大驱动力、驱动滚筒奔离点的松边张力、驱动滚筒趋入点的紧边张力(输送带最大张力)所决定的。驱动滚筒所传递的最大驱动力由带式输送机工况的运行阻力来决定, 不同工况下运行阻力不同。因此, 张紧力的大小由运行工况来确定。张紧力与驱动滚筒张力的示意图如图 3所示。
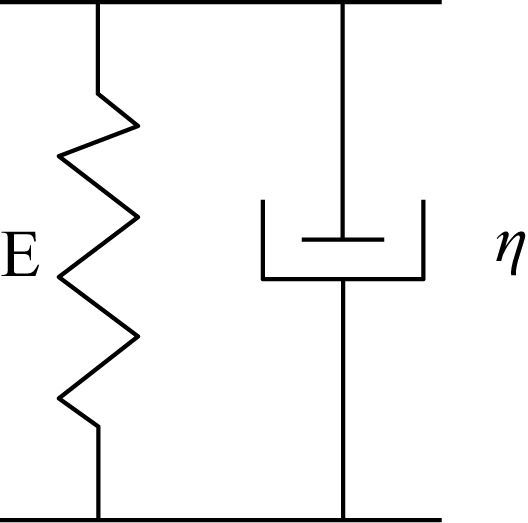 |
| 图 2 Kelvin模型 |
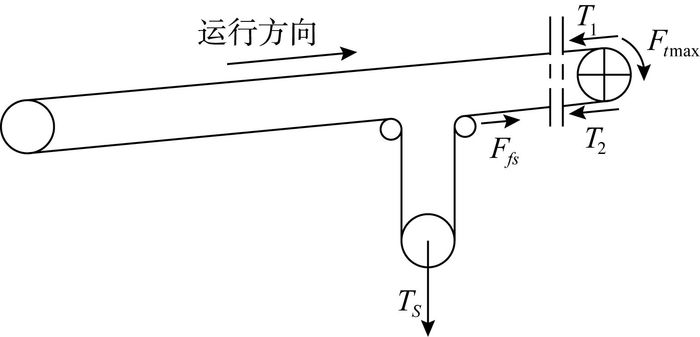 |
| 图 3 张紧力与驱动滚筒张力关系示意图 |
驱动滚筒所传递的最大驱动力、松边张力、紧边张力及张紧力之间的相互关系表达如下:
| $ {T_2} \ge \frac{{{F_{t\max }}}}{{{e^{\mu \alpha }} - 1}} $ | (9) |
| $ {T_1} = {T_2} + {F_{t\max }} $ | (10) |
| $ {T_s} = 2\left( {{T_2} + {F_{fs}}} \right) $ | (11) |
式中, Ftmax为驱动滚筒的驱动力(N);μ为输送带与滚筒间的摩擦系数;α为输送带在驱动滚筒上的围包角(°);T1为驱动滚筒紧边张力(N);T2为驱动滚筒松边张力(N);Ts为张紧力(N);Ffs为拉紧装置与驱动滚筒之间输送带的运行阻力(N)。
3.4 驱动装置建模离合器建模中主要考虑扭矩控制和接合规律。变速器建模中主要考虑变速器类型选择和换挡规律的制定。
根据式(4)来确定不同挡位所需离合器的控制扭矩。传动效率需要试验才能确定, 为简化分析, 文中忽略了传动效率。
带式输送机是大负载、大运行阻力的机械。离合器分离后, 由于带速比较低, 输送带在运行阻力的干扰下带速会急速下降, 加速度出现负值。根据离合器接合四个阶段的不同特点, 遵循离合器“快-慢-快”的接合规律, 接合过快会给系统造成较大的冲击, 接合过慢则会使离合器滑磨时间变长。基于离合器接合规律的要求, 确定离合器分离和接合时间的仿真参数:分离时间0.05 s、接合时间0.4 s[18]。
半接合点离合器控制扭矩由输送机的运行阻力和变速器、减速器的传动比来确定, 即为前面公式(3)所确定的等效阻力矩。按照半接合点之前慢、之后快的接合规律, 离合器的接合规律为:消除离合器自由间隙时间0.05秒, 自由间隙消除到半接合点之前0.25秒, 半接合点之后至加速控制扭矩之前0.10秒。
采用单参数换挡规律, 以各个挡位的目标带速为换挡依据, 确定换挡时刻。换挡时间的仿真参数为0.4 s(摘挡时间0.1 s, 选挡时间0.1 s, 换挡时间0.2 s)。
在AMESim环境下建立AMT软起动带式输送机模型[19], 仿真模型如图 4所示。接下来依据所建立的模型研究满载工况下1挡起动过程和1-8挡换挡过程中系统参数的变化。
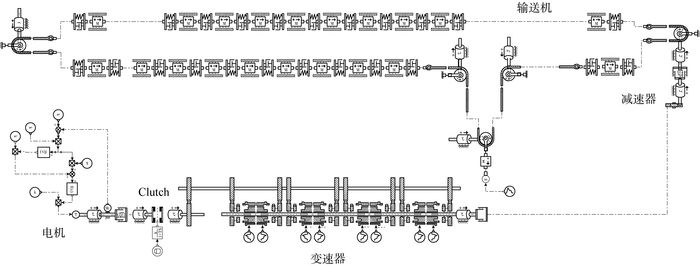 |
| 图 4 AMT软起动带式输送机AMESim模型 |
4 满载工况1挡起动仿真分析
以离合器分离完毕时刻计为0时刻, 之前10 s施加张紧力, 之前2 s空挡起动电机。1挡起动过程主要讨论输送带速度、输送带加速度传递扭矩的变化情况。
从带速曲线可以看出:与头部相比, 输送带尾部的起动有滞后现象, 起动过程中输送带速度稳定上升。
从起动加速度曲线可以看出:(1)起动过程中输送带头部与尾部的加速度波动稍有不同, 尾部的加速度峰值略高;(2)起动过程中输送带的加速度最大峰值0.3 m/s2。
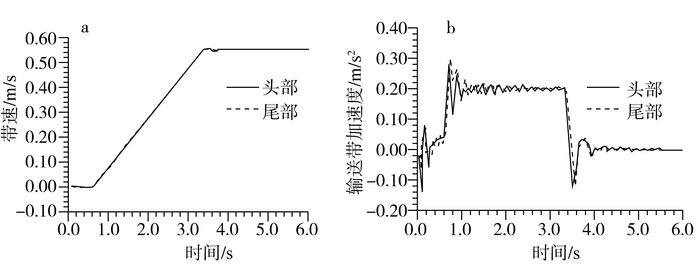 |
| 图 5 满载工况1挡起动过程仿真结果 |
5 满载工况换挡过程仿真分析
AMT软起动带式输送机的基本要求:从低挡依次换挡至高挡的过程中, 输送带由低速爬行逐步加速到目标运行速度(4.303 m/s)并保持稳定运行, 系统主要特征参数的变化在许用范围之内, 输送带的附加动张力尽量小。
换挡过程主要研究输送带、驱动滚筒、离合器、变速器等主要部件特征参数的变化。
5.1 输送带仿真结果换挡过程中带速和输送带加速度的仿真结果如图 6所示。
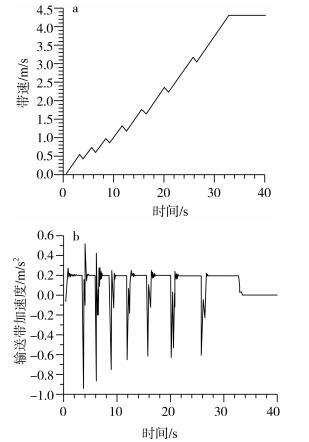 |
| 图 6 换挡过程中带速和输送带加速度变化曲线 |
从带速曲线可以看出:随着挡位的增加, 带速稳定上升, 换挡过程中带速稍有下降。仿真时间至33.10 s时, 输送带达到目标带速4.303 m/s。
从加速度曲线中可以看出:换挡过程中离合器接合瞬间存在短时的加速度突变现象, 之后输送带加速度值趋于稳定, 值为0.2 m/s2, 8挡加速完成后加速度为0, 输送带进入匀速运行阶段。换挡过程中输送带加速度峰值不超过1 m/s2, 对输送带上的物料运行影响不大。
5.2 驱动滚筒仿真结果换挡过程中驱动滚筒处紧边张力和输出扭短的仿真结果如图 7所示。从驱动滚筒紧边张力曲线可以看出:换挡过程中输送带加速度突变引起驱动滚筒紧边张力的突变。驱动滚筒处紧边张力峰值近70 kN, 输送带稳定加速阶段紧边张力在60290 N附近波动, 加速完成后紧边张力保持在45385 N。可见换挡过程中输送带的附加动张力低于10 kN。输送带的纵向拉伸强度为1250 N/mm, 则输送带纵向可承受拉伸力1500 kN。因此驱动滚筒最大张力峰值没有超过输送带拉伸极限。
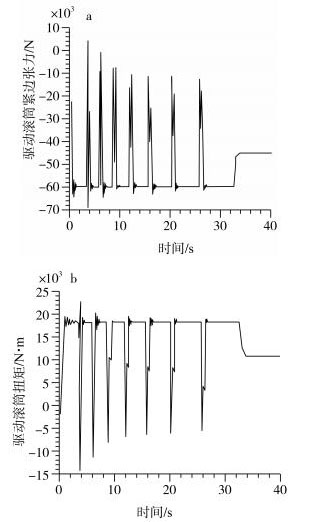 |
| 图 7 换挡过程中驱动滚筒紧边张力和扭矩曲线 |
从驱动滚筒扭矩曲线可以看出:换挡过程中输送带加速度突变引起驱动滚筒扭矩突变。驱动滚筒扭矩变化峰值可达到23 dN·m, 加速时所需驱动滚筒扭矩计算值为18.37 kN·m, 两者差值为5 kN·m, 加速完成后, 驱动滚筒处扭矩稳定在10920 N·m。因此, 驱动滚筒扭矩变化峰值没有超过驱动滚筒许用扭矩极限值52 kN·m。
5.3 离合器、变速器仿真结果换挡过程中离合器、变速器输出扭矩的仿真结果如图 8所示。
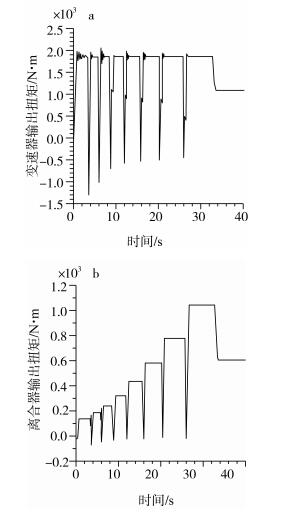 |
| 图 8 换挡过程中AMT驱动装置扭矩曲线 |
从变速器输出扭矩曲线可以看出:输送带加速度突变引起变速器输出扭矩突变。换挡过程中变速器输出扭矩变化峰值可达到2 100 N·m, 加速完成后变速器输出扭矩基本稳定在1 092 N·m。从离合器输出扭矩曲线可以看出:换挡过程中离合器输出扭矩曲线过度平滑, 离合器最大输出扭矩即为变速器输入扭矩, 没有超出变速器最大输入扭矩1 900 N·m的使用要求。因此, 离合器接合规律合理。
6 结论1) 分析了AMT软起动带式输送机的工作原理, 建立了离合器控制扭矩与输送带加速度之间的关系, 指出通过控制离合器传递扭矩可控制输送带的加速度。
2) 建立了等加速度控制AMT软起动带式输送机模型, 以110 kW平运单点驱动带式输送机为例, 依据提出的离合器接合规律和换挡规律对模型进行了仿真分析。仿真结果表明, 0.2 m/s2等加速度控制AMT软起动带式输送机的设计是合理的。
3) AMT换挡期间不可避免存在动力中断, 并带来输送带加速度突变等系统特征参数的变化, 输送带的加速度峰值不超过1 m/s2, 离合器、变速器、驱动滚筒等特征曲线的变化没有超出产品的许用极限。
| [1] |
厉伟, 王帆, 李海波, 等. 带式输送机软起动调速控制器设计[J]. 沈阳工业大学学报, 2008, 30(4): 374-378, 398. |
| [2] |
ROCHA A. V., FRANCA G. J., DOS SANTOS M. E., et al. Increasing long belt-conveyors availability by using fault-resilient medium voltage AC drives[C]. Industry Applications Society Annual Meeting (IAS), 2011 IEEE, 2011:1-8.
|
| [3] |
HARRISON A. Belt conveyor research 1980-2000[J]. Bulk Solids Handling, 2001, 21(2): 159-164. |
| [4] |
李玉瑾. 带式输送机的动态特性分析与软起动设计[J]. 煤炭学报, 2002, 27(3): 29-299. |
| [5] |
宋伟刚. 通用带式输送机设计[M]. 北京: 机械工业出版社, 2006.
|
| [6] |
NORDELL L K. The channar 20km overland-a flagship of modern belt conveyor technology[J]. Bulk Solids Handling, 1991, 11(4): 781-792. |
| [7] |
ARRISON A., ROBERTS A. W. Technical requirements for operating conveyor belts at high speed[J]. Bulk Solids Handling, 1984, 4(1): 99-104. |
| [8] | |
| [9] |
余荣辉, 孙冬野, 秦大同. 机械自动变速系统动力性换挡控制规律[J]. 农业机械学报, 2006, 37(4): 1-4. |
| [10] |
何忠波, 白鸿柏, 张培林, 等. AMT车辆坡道换挡策略与试验研究[J]. 农业机械学报, 2007, 38(2): 13-16. |
| [11] |
葛安林. 车辆自动变速理论与设计[M]. 北京: 机械工业出版社, 1993.
|
| [12] |
孔慧芳. 电控机械式自动变速器中传动与控制的关键技术研究[D]. 合肥工业大学博士论文, 2007: 28-52.
|
| [13] |
韩刚. 带式输送机输送带弹性模量的测试[J]. 起重运输机械, 1998(3): 31-33. |
| [14] |
谢丽蓉, 王智勇, 晁勤. 鼠笼异步电动机机械特性的研究[J]. 中国电机工程学报, 2008, 28(21): 68-72. |
| [15] |
宋伟刚, 邓永胜, 郭立新. 基于功率跟踪控制策略的带式输送机动态设计方法[J]. 东北大学学报(自然科学版), 2002, 23(9): 899-902. |
| [16] |
宋伟刚, 王丹. 7.6km长距离带式输送机系统动力学的计算机仿真[J]. 煤炭学报, 2004, 29(2): 249-253. |
| [17] |
ZUR T. W. Viscoelastic properties of conveyor belts-modeling of vibration phenomena in belt conveyors during starting and stopping[J]. Bulk Solids Handing, 1986, 6(3): 553-560. |
| [18] |
葛安林, 高炳钊, 牛铭奎, 等. AMT车辆液压系统的仿真与应用[J]. 汽车工程, 2002, 24(5): 376-37. |
| [19] |
付永领, 祁晓野. AMESim系统建模和仿真——从入门到精通[M]. 北京: 北京航空航天大学出版社, 2006.
|
 2017, Vol. 31
2017, Vol. 31


