| 基于互惠食饵捕食模型的草原放牧稳定性的研究 |
草地资源虽然属于可再生资源, 但过度使用会使得温带草原退变为荒漠草原最终变为荒漠, 所以需要对草原资源实施科学管理控制。牧民们赖以生存的草原系统属于比较脆弱的生态系统, 因此保护草原系统尤为重要。为保持草原可持续发展, 研究放牧数量和牧草之间的关系可提供理论依据。
安玉锋等[1]采用放牧系统动态模型描述特定空间内牧草和家畜量变过程, 发现牧草增长率和绵羊种群采食率轨迹图中出现2个平衡点, 2个点之间的牧草生产量有贮存效应, 2点之外为存在缺草期, 只有发挥系统耦合的效应能力方可使放牧系统健康发展。张彦宇等[2]在草原放牧系统管理的问题中考虑到环境因素(降水、温度等)存在周期性变化及放牧周期的干扰, 建立存在周期制约作用的草地放牧系统管理的最优控制模型。张慧玲等[3]通过实验就不同耗牛放牧强度对牧草生长的环境进行了研究, 实验结果表明禁止放牧和高强度放牧均会使草原呈现“双向退化现象”, 轻度放牧则会使得牧草保持良好的生长状态。Majumdar Prahlad等[4]研究Caputo型分数阶3种群食物链模型时, 讨论了所需参数条件下的所有可能平衡点。
上述研究对草原牧草和放牧数量进行了系统分析, 牧草和放牧数量之间存在平衡点, 放牧强度过高或者过低, 均对草场不利。但是这些研究几乎都未提及一个重要的因素, 即草场和放牧的牲畜是相互作用和影响的。牧草可为牲畜提供营养, 同样牲畜排除的粪便可作为无机肥料为牧草供给养料[5-8], 因此二者之间存在一种互惠关系。本文考虑牧草和牲畜的互惠关系及阻滞性, 采用食饵捕食模型研究牧草和放牧数量存在的平衡点问题。
1 未考虑自身阻滞一般模型建立食饵捕食模型[9]是生态学中比较常见的数学模型, Volterra模型讲述食饵在不被外界因素影响而独立生长的情况下是呈指数增长的, 从而草在不被影响下也为指数增长, 不妨设草的相对增长率为r1, 则草在t时刻增长率可以用方程表示
| $ x^{\prime}(t)=r_{1} x, $ | (1) |
羊的存在使得草的数量不断减少, 即草在x′(t)时刻的增长率减少, 将(1)改进后, x′(t)满足方程
| $ x^{\prime}(t)=r_{1} x-\sigma_{1} x y, $ | (2) |
其中,σ1为单位数量羊吃草的能力。
同样, 在没在有人工喂养情形下, 羊群离开牧草无法生存, 因此没有牧草时, 会出现负增长。假设羊群在不被外界投喂的情况下独立生存时死亡率为a, 则羊在t时刻的增长率表达式为
| $ y^{\prime}(t)=-a y。$ | (3) |
牧草为羊提供丰富的食物, 从而减少羊的死亡率并且促进羊群数量的增加, 则更为精确的羊在t时刻增长率表达式为
| $ y^{\prime}(t)=-a y+\sigma_{2} x y, $ | (4) |
其中,σ2为单位数量草对羊的供养能力。
草相当于食饵捕食模型中的食饵, 依靠肥沃的土壤和适量的降水等自然资源得以生长, 羊则为捕食者需要以草为生。联立方程(2)和(4)求稳定点
| $ \left\{\begin{array}{l} r_{1} x-\sigma_{1} x y=0 \\ -a y+\sigma_{2} x y=0 \end{array}\right.。$ | (5) |
解得2个稳定点(0, 0)与
通过MATLAB做出式(2)和(4)关系图像如图 1所示。由图 1可知, 牧草和羊群之间联系密切, 随着牧草的增多, 羊群的数量会急剧上升, 达到一定值羊群之间的相互竞争, 牧草的数量会急剧减少, 羊的数量也会随之减少, 循环往复呈周期性变化。随时间变化, 并没有出现相对稳定的状态, 因此可推测平衡点不稳定。
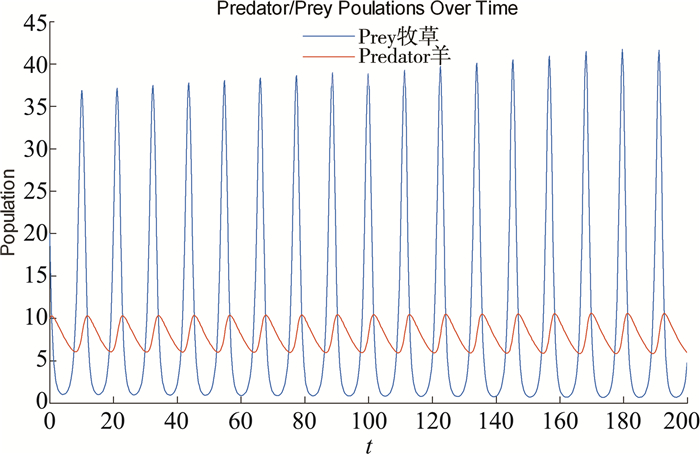 |
| 图 1 牧草和羊群在一般模型下随时间变化关系图像 |
2 互惠模型建立
在饲养牲畜过程中, 羊群或者草均存在自己与自己的竞争, 即常说的自身阻滞。在考虑自身阻滞条件下, 还要加入物种之间相互影响的因素, 即若牧草增多, 则羊群也会随之增加, 直至增加到一个平衡点, 超过平衡点以后羊群和牧草的数量均会下降。为保证牧草的可持续增长, 需要将放牧强度控制在一定范围, 因此研究放牧强度和牧草平衡点[10-11], 采用更加精确的模型:
| $ x^{\prime}(t)=F(x, y)=r_{1} x\left(1-\frac{x}{N_{1}}+\sigma_{1} \frac{y}{N_{2}}\right), $ | (6) |
式中x(t)表示在t时刻牧草的数量, r1为草的相对增长率, N1为温带草原上能容纳草的数量, N2为草原上能容纳羊的最大数量。
| $ y^{\prime}(t)=G(x, y)=r_{2} y\left(-1+\sigma_{2} \frac{x}{N_{1}}-\frac{y}{N_{2}}\right), $ | (7) |
式中y(t)表示在t时刻放牧羊的数量, r2为羊的相对增长率, σ1和σ2反映的是草和羊之间相互的供养能力。
联立(6)和(7)式:
| $ \left\{\begin{array}{c} r_{1} x\left(1-\frac{x}{N_{1}}+\sigma_{1} \frac{y}{N_{2}}\right)=0 \\ r_{2} y\left(-1+\sigma_{2} \frac{x}{N_{1}}-\frac{y}{N_{2}}\right)=0 \end{array}\right.。$ | (8) |
求得3个平衡点分别为(0, 0)、(N1, 0)、
考察平衡点是否稳定有直接法和间接法两种基本方法, 本文采用直接法判断[12-13]。直接法对于一些不能求精确解的方程使用起来非常方便, 可在不知方程解的情况下直接判断平衡点稳定性。首先求得方程组的系数矩阵为
| $ H=\left[\begin{array}{ll} F_{x} & F_{y} \\ G_{x} & G_{y} \end{array}\right], $ | (9) |
其中对方程组系数矩阵中各元素求导如下
| $F_{x}=r_{1}\left(1-\frac{2 x}{N_{1}}+\sigma_{1} \frac{y}{N_{2}}\right), $ | (10) |
| $F_{y}=\frac{r_{1} \sigma_{1} x}{N_{2}} , $ | (11) |
| $G_{x}=\frac{r_{2} \sigma_{2} y}{N_{1}}, $ | (12) |
| $G_{y}=r_{2}\left(-1+\frac{\sigma_{2} x}{N_{1}}-\frac{2 y}{N_{2}}\right) 。$ | (13) |
令m=-(Fx+Gy), n=|H|。平衡点稳定需要满足条件为m>0, n>0;若计算出m<0或者m<0则平衡点均看作是不稳定的。因为稳定点才能作为牧草和羊群放牧强度的阈值, 所以要判断平衡点是否稳定。
将平衡点(0, 0)代入得m=r1-r2(σ2-1), n=-r1r2(σ2-1), 不满足平衡点稳定条件; 将平衡点(N1, 0)代入得m=r1-r2(σ2-1), n=-r1r2(σ2-1), 当σ2<1时满足平衡点稳定条件, 但是却不符合实际, 因为羊群的数量不可能为0, 所以将此平衡点排除。接下来主要研究平衡点
(a) σ1<1, σ2>1, σ1σ2<1时, 第3个平衡点满足条件, 因此该平衡点是稳定的, 牧草和羊群数量在此平衡点附近最有利于两种群生存。
(b) σ1>1, σ2<1, σ1σ2>1时, 第3个平衡点n<0, 因此不满足平衡条件, 平衡点在这种条件下是不稳定的。
给定符合(a)条件的模拟值r1=4, σ1=0.9, r1=0.5, σ2=1.1, N1=300, N2=200, 通过MATLAB做出式(6)和(7)关系图像如图 2所示。由图像可知随着牧草的增多羊群数量也是增加的, 最终趋于稳定。相较于一般模型, 此模型震荡较较小, 比较平稳, 但是长时间将放牧数量控制在稳定的平衡点附近, 也是不利于牧草生长的, 因为长时间的啃食踩踏会导致土壤质量下降。
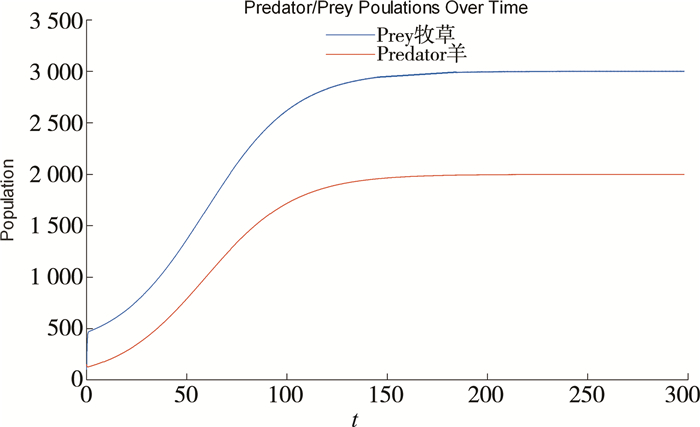 |
| 图 2 牧草和羊群在阻滞模型下随时间变化趋势 |
3 模型优化
倘若将牲畜长时间集中在一个地方放牧, 牲畜长时间啃食践踏牧草, 会造成土壤板结化, 这对牧草可持续生长非常不利[14]。因此为保护牧草再恢复, 不防将牧草分为成年草和幼年草, 对于还未长大的幼年草实施保护, 可以将牧区划片让牲畜去成年草草场吃草, 待到幼年草草场长大, 再将牲畜驱赶至长大的幼年草草场[15-16]。建立含有幼年草增长率项的成年草微分方程:
| $ X^{\prime}(t)=r_{3} Y-\sigma_{3} X Z-b_{1} X+\sigma_{4} Z, $ | (14) |
其中t时刻放牧成年草的数量、不能放牧幼年草的数量以及放牧羊的数量分别用X(t)、Y(t)、Z(t)表示; r3反映草的增长率, 即幼年草长为成年草的效率, 与上文提到的r1类似; σ3也与上文涉及的σ1相仿, 即表示羊吃草的能力。相较于(2)式, 此模型多了后两项, b1为草在环境竞争作用下存在的死亡率, b1X可理解为自身阻滞项; σ4与上文表达σ3含义相近, 即反映羊群对牧草的供养能力或者促进能力。
建立幼年草增长率模型:
| $ Y^{\prime}(t)=\sigma_{5} X-b_{1} Y, $ | (15) |
其中σ5为幼年草长为成年草率。
| $ Z^{\prime}(t)=\sigma_{6} X Z-b_{2} Z, $ | (16) |
其中σ6反映牧草对羊群的供养能力, b2表示羊群之间的竞争存在的死亡率。此方程与(4)表达含义一样。将(14)、(15)和(16)方程联立得
| $ \left\{\begin{array}{l} X^{\prime}(t)=0 \\ Y^{\prime}(t)=0 \\ Z^{\prime}(t)=0 \end{array}\right.。$ | (17) |
不符合实际的平衡点不予考虑, 故只考虑有意义平衡点, 通过计算和取舍后得到平衡点
给式子(14)、(15)、(16)的参数r3、σ3、b1、σ4、σ5、σ6、b2数值, 通过MATLAB软件编程, 来验证平衡点的稳定性。将r3=4, σ3=0.5, b1=0.1, σ4=0.1, σ5=0.2, σ6=0.01, b2=0.04代入(14)、(15)、(16), 可得到成年草、幼年草以及羊群的增长率关系图像, 如图 3所示。
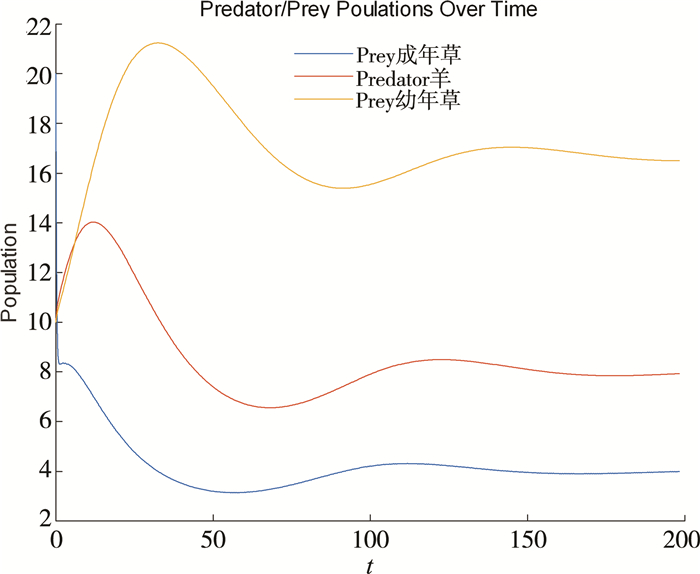 |
| 图 3 幼年草、成年草以及羊群三者关系随时间变化关系 |
给定幼年草、成年草以及羊群一定的初始值后, 可模拟出三者随时间变化的图像。由图 3可知随着时间的变化羊群数量出现短期的增加, 它们主要以成年草为食, 因此导致成年草的数量减少。而幼年草不被啃食, 从而得到保护得以安全长大, 数量会急剧上升。虽然三者关系刚开始出现很大波动, 但是最终三者会达到稳定状态, 因此平衡点
(1) 一般模型中考虑的系统非常理想, 牧草和羊群的相互影响较大, 一方变化会导致另一方出现很大的波动, 因此平衡点是不稳定的。
(2) 在互惠模型中, 考虑牧草和羊群都存在自身的阻滞, 并且还考虑了羊群的啃食和排泄物会促使牧草增长, 模型中求的平衡点是稳定的, 然而长时间在一个地方放牧不利于牧草生长。
(3) 优化模型中, 将牧草分为成年草和幼年草, 实际上可看作两类食饵一类捕食者的模型, 从优化模型中得到稳定的平衡点, 求得牧草和羊群的数量关系最好维持在平衡点附近。
(4) 通过对一般模型、互惠模型以及优化模型比较, 得出放牧最好采取分区放牧的结论。牧草划区放牧不但可以实现牧民利益最大化, 还可以实现牧草的可持续利用。
(5) 根据对牧草和放牧强度的分析可采取以下举措: 分类划片放牧, 将牧草分为幼年草和成年草, 羊群分为大型羊和小型羊; 按季节轮牧, 将牧区分为春夏秋冬四季。
| [1] |
安玉锋, 李峻成, 王钦, 等. 高山草原放牧系统控制的研究[J]. 草业学报, 2002, 11(3): 66-71. |
| [2] |
张彦宇, 李文龙, 韩晓卓, 等. 存在周期制约作用的草原放牧系统管理的最优控制模型及其应用[J]. 兰州大学学报, 2006(2): 106-109. |
| [3] |
张慧玲, 高啟贤. 天祝抓喜草原不同牦牛放牧强度对牧草生长的影响[J]. 中国牛业科学, 2019, 45(5): 37-39. |
| [4] |
MAJUMDAR PRAHLAD, MONDAL BAPIN, DEBNATH SURAJIT, et al. Controlling of periodicity and chaos in a three dimensional prey predator model introducing the memory effect[J]. Chaos, Solitons and Fractals: the Interdisciplinary Journal of Nonlinear Science, and Nonequilibrium and Complex Phenomena, 2022, 164: 960-779. |
| [5] |
王兴, 宋乃平, 杨新国, 等. 羊粪归还对荒漠草原表层土壤碳氮的影响[J]. 水土保持通报, 2013, 33(5): 6-10. |
| [6] |
SHANKAR ARUN, PAL RAJESH KUMAR, RANJAN RAHUL, et al. Ameliorating effect of organic materials on saline-sodic soil in central ganga plain in uttar Pradesh, India[J]. Communications in Soil Science and Plant Analysis, 2022, 53(19): 2655-2661. DOI:10.1080/00103624.2022.2072865 |
| [7] |
DONG D, YANG W C, SUN H, et al. Effects of animal manure and nitrification inhibitor on N2O emissions and soil carbon stocks of a maize cropping system in northeast China[J]. Scientific Reports, 2022, 12(1): 15202-15202. DOI:10.1038/s41598-022-19592-9 |
| [8] |
ZHANG M, LI X, LI M, et al. Effects of grazing on soil organic carbon in the rhizosphere of stipa grandis in a typical steppe of inner Mongolia, China[J]. Sustainability, 2022, 14(19): 11866-11866. |
| [9] |
杨巧艳, 廖代琴, 颜向平. 具有时滞的Lotka-Volterra食饵-捕食者成年种群模型的稳定性分析[J]. 应用数学, 2022, 35(4): 966-973. |
| [10] |
张倩. 一类捕食者-食饵-互惠模型的稳定性分析[J]. 兰州文理学院学报(自然科学版), 2016, 30(1): 9-12. |
| [11] |
PAUL CULL, KATIE WALSH, JON WHERRY. Stability and instability in one dimensional population models[J]. Scientiae Mathematicae Japonicae, 2020, 67(2): 105-124. |
| [12] |
王景艳, 杨艳丽. 微分方程的平衡点及稳定性分析[J]. 保山学院学报, 2010, 29(2): 52-54. |
| [13] |
刘锐宽. 一类二阶微分系统奇点稳定性的判断[J]. 焦作工学院学报(自然科学版), 2001(6): 485-488. |
| [14] |
李梦然. 不同载畜率下短花针茅草原N2O通量及相关微生物的研究[D]. 呼和浩特: 内蒙古农业大学, 2020.
|
| [15] |
卢雪丽. 一类带阶段结构的食饵—捕食者交错扩散模型的非线性不稳定性[D]. 兰州: 兰州交通大学, 2015.
|
| [16] |
邱丽华. 一类具有常数迁移率和年龄结构的食饵—捕食模型[D]. 广州: 广州大学, 2018.
|
 2023, Vol. 37
2023, Vol. 37


