齐鲁工业大学学报   2018, Vol. 32 Issue (5): 16-21
0
引用本文
董志敏, 徐培波, 张颜辉, 等. 新型超卤素阴离子MX3-(M=Be, Mg, Ca;X=F, Cl, Br)的理论研究[J]. 齐鲁工业大学学报, 2018, 32(5): 16-21. DOI: 10.16442/j.cnki.qlgydxxb.2018.05.004
DONG Z M, XU P B, ZHANG Y H, et al. Theoretical Study on Novel Superhalogen Anions MX3-(M=Be, Mg, Ca;X=F, Cl, Br)[J]. Journal of Qilu University of Technology, 2018, 32(5): 16-21. DOI: 10.16442/j.cnki.qlgydxxb.2018.05.004
新型超卤素阴离子MX3-(M=Be, Mg, Ca;X=F, Cl, Br)的理论研究[PDF全文]
董志敏, 徐培波, 张颜辉, 史相强, 柳兆良, 郭丽华, 李连鑫, 杨晓勇     
齐鲁工业大学(山东省科学院) 化学与制药工程学院，济南 250353
收稿日期: 2018-06-25; 网络出版时间: 2018-10-31
基金项目: 大学生创新创业训练计划项目（04120482）
作者简介: 董志敏(1996-), 本科生; 研究方向:超卤素原子的设计.
通讯作者: 杨晓勇(1974-), 硕士、讲师; 研究方向:新型分子的理论研究; zidu113@163.com.
摘要：从理论上考察了一种新型超卤素阴离子体系MX3-（M=Be，Mg，Ca；X=F，Cl，Br），并对该体系的几何结构、成键特征等性质进行了详细研究。上述MX3-的全实频率的几何优化结构在MP2/6-311+G（d）水平下得到并进行自然键轨道（NBO）分析，证实所有的MX3-均具有平面几何结构。所研究的MX3-表现出相当大的HOMO-LUMO能隙值，说明它们具有很好的稳定性。这些MX3-的电离势IP值均高于Cl原子的电子亲和势EA值，因此可以视其为超卤素阴离子。量子化学计算结果表明MX3-体系中卤素配体的原子尺寸可以影响其电离势值：配体尺寸越小，电离势值越低。
关键词：超卤素    电子亲和势(EA)    电离势    量子化学计算    
Theoretical Study on Novel Superhalogen Anions MX3-(M=Be, Mg, Ca;X=F, Cl, Br)
DONG Zhi-min, XU Pei-bo, ZHANG Yan-hui, SHI Xiang-qiang, LIU Zhao-liang, GUO Li-hua, LI Lian-xin, YANG Xiao-yong     
School of Chemistry and Pharmaceutical Engineering, Qilu University of Technology(Shandong Academy of Sciences), Jinan 250353, China
Abstract: In this work, a new kind of superhalogen anion MX3- (M=Be, Mg, Ca; X=F, Cl, Br) was investigated by quantum chemical method.Their structures, bonding features and other properties were discussed in detail.The geometries of these MX3- with all real frequencies are optimized by MP2 method with 6-311+G(d) basis set.The natural bond orbital(NBO) analysis is performed at the MP2/6-311+G(d) level.All these MX3- species present stable planar structure.The stability of the studied MX3- species is guaranteed by considerable HOMO-LUMO gaps.The ionization potential(IP) of these MX3- species is higher than the EA of Cl atom, hence they can be considered as superhalogen anions.Quantum chemistry calculation results also reveals that the 'size' of the halogen ligand plays an important role in the IP value:the smaller the halogen ligand, the higher the IP value.
Key words: superhalogen    electron affinity(EA)    ionization potential(IP)    quantum chemistry calculation    

理论化学领域的先驱者Khanna和Jena[1]提出, 具有封闭的原子和电子结构的团簇可以称作超原子。超原子可以像砖块一样堆砌成化合物团簇或离子, 这种化合物团簇或离子可以非常稳定地存在, 表现出类似某一单个原子的性质[2-3]。超原子主要分为超卤素(Superhalogen)[4]和超碱金属(Superalkalies)两种类型[5-6]。超卤素是具有比卤素原子(3.0~3.6 eV)更高的电子亲和能的原子团簇。由于超卤素具有非常高的电子亲和势, 并表现出很强的氧化性, 越来越多的这样的分子被应用在合成新的化合物的领域。

我们设计了一种新型超卤素阴离子体系MX3-(M=Be, Mg, Ca; X=F, Cl, Br)。设计出30种超卤素阴离子结构模型并完成结构优化; 分析体系中X配体电负性(配体原子尺寸)与电子亲和势之间的关系。此研究工作将为实验以及理论科学工作者设计新型超卤素提供方向和理论预测, 有助于设计出更多类型的超卤素。

1 计算方法

首先, 考虑了M(M=Be, Mg, Ca; X=F, Cl, Br)之间所有可能的相互作用方式, 寻找超卤素阴离子体系(M=Be, Mg, Ca; X=F, Cl, Br)的所有可能的异构体。并使体系在没有任何对称性限制下, 在MP2/6-311+G(d)水平下进行优化。振动频率和自然键轨道NBO[7]分析是采用与几何优化相同的计算水平下获得的。在计算电子亲和势的时候, 为了保证结果的可靠性, 采用了两种方法。第一种方法是在优化之后的阴离子体系的结构基础上, 采用6-311+G(d)基组, 利用OVGF方法[8-10]计算其阴离子体系MX3-的垂直电子电离能。这是由于其阴离子体系的垂直电子电离能近似于中性体系的第一电子亲和势。第二种方法则是在优化后的中性体系的结构基础上, 分别计算其阴离子体系和中性体系的能量, 两者做差, 最后得到电子亲和势。

所有的计算均使用GAUSSIAN 03程序包完成[11], 所有图形使用Gauss View程序绘出[12]。

2 结果与讨论 2.1 几何构型

在考虑了M(M=Be, Mg, Ca)和X(X=F, Cl, Br)之间所有可能的相互作用方式之后, 在MP2/6-311+G(d)水平下优化得到了超卤素阴离子体系MX3-(M=Be, Mg, Ca; X=F, Cl, Br)的30个具有全实频率结构的异构体[13-15], 示意图参见图 1, 结构见图 2。超卤素阴离子体系MX3-的结构对称性、几何参数、最低振动频率ν(cm-1)以及HOMO-LUMO能隙值Gap(eV)列于表 1中。

图 1 超卤素阴离子体系MX3-的几何结构示意图

图 2 超卤素阴离子MX3-的平衡几何结构图

表 1 超卤素阴离子MX3-的结构对称性、几何参数、最低振动频率ν以及HOMO-LUMO能隙值Gap

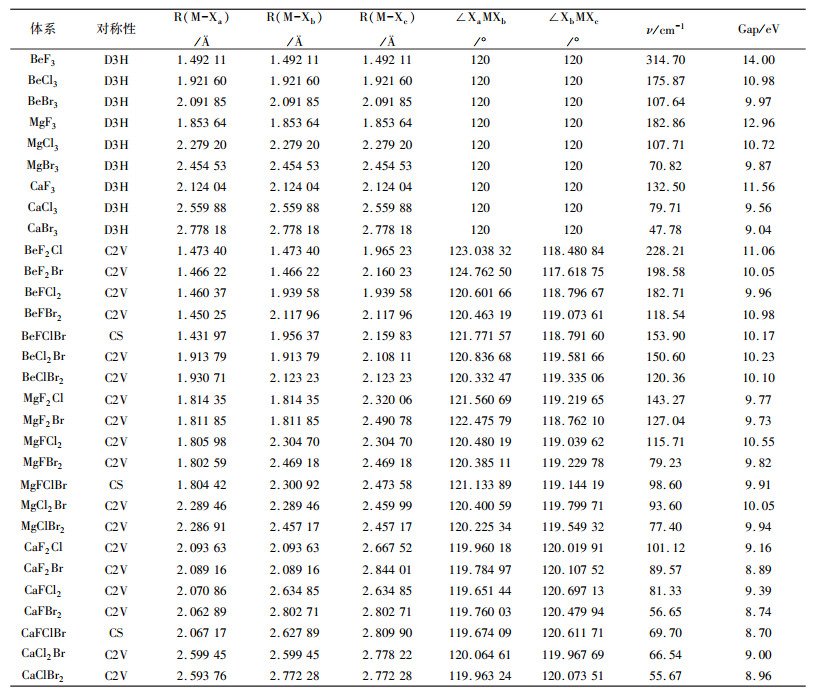从图 1、图 2以及表 1中可以看出:在MP2/6-311+G(d)水平下计算出的30种超卤素阴离子MX3-体系均具有平面几何结构。表 1中的最低振动频率ν(cm-1)显示所计算的所有结构振动频率全部无虚频, 这说明优化所得的30个结构都是势能面上的极小点, 是稳定构型。另外, 对于所研究的新型超卤素阴离子体系MX3-的化学活性和结构稳定性, 可以通过计算最高占据轨道(HOMO)与最低非占据轨道(LUMO)之间的能量差来衡量。在表 1中, 可以看出所有超卤素阴离子体系MX3-的能隙值都非常大, 分别在8.70—14.00 eV之间, 如此大的能隙值证明了这些物质结构都是可以稳定存在的。此外, 不难发现规律:能隙值随卤素配体原子被更大的卤素原子取代而单调减小。比如:BeX3-(14.00 eV)> BeF2Cl-(9.77 eV)>BeF2Br-(9.73 eV)。由于HOMO-LUMO能隙值越高, 体系化学性质越不活跃, 因此, 随着能隙值的逐渐降低, 这些超卤素阴离子体系MX3-得到电子的能力也逐渐增加, 活性逐渐增强。

为了方便讨论, 将超卤素阴离子体系MX3-中的卤素配体进行编号Xa、Xb、Xc(如图 1所示), 即将超卤素表示为MXaXbXc。如表 1所示, 这些超卤素分子的最低能量结构分别为:

1) D3H:BeF3、BeCl3、BeBr、MgF3、MgCl3、MgBr3、CaF3、CaCl3、CaBr3

2) C2V:BeF2Cl、BeF2Br、BeFCl2、BeFBr2、BeCl2Br、BeClBr2、MgF2Cl、MgF2Br、MgFCl2、MgFBr2、MgCl2Br、MgClBr2、CaF2Cl、CaF2Br、CaFCl2、CaFBr2、CaCl2Br、CaClBr2

3) CS:BeFClBr、MgFClBr、CaFClBr

由于配体卤素原子的性质影响着MX3的结构, 在下面的讨论中, 将详细研究改变配体原子X对MX3结构的影响。以Be-F键为例:在所有体系中, 最大的Be-F键长出现在分子BeF3(1.492 11 Ä)中, 最小的Be-F键长出现在分子BeFClBr(1.431 97 Ä)中。随着BeF3分子中Xc配体的变化顺序为:F→Cl→Br, Be-Fa和Be-Fb的键长变化为:BeF3(1.492 11 Ä)>BeF2Cl(1.473 40 Ä)>BeF2Br(1.466 22 Ä)。这就说明, 用Cl和Br原子取代BeF3中的F原子可以逐渐减小Be-F键长。同样的, 当MgF3、CaF3分子中的Xc配体按F→Cl→Br顺序变化时, 在Mg-Fa、Mg-Fb和Ca-Fa、Ca-Fb的键长变化中, 也出现了相同的规律:MgF3(1.853 64 Ä)>MgF2Cl(1.814 35 Ä)>MgF2Br(1.811 85 Ä); CaF3(2.124 04 Ä)>CaF2Cl(2.093 63 Ä)>CaF2Br(2.089 16 Ä)。

以Be-Cl键为例:在所有体系中, 最大的Be-Cl键长出现在分子BeFCl2(1.939 58 Ä)中, 最小的Be-Cl键长出现在分子BeCl2Br(1.913 79 Ä)中。随着BeCl3分子中Xc配体的变化顺序为:F→Cl→Br, Be-Cla和Be-Clb的键长变化为:BeFCl2(1.939 58 Ä)>BeCl3(1.921 60 Ä)>BeCl2Br(1.913 79 Ä)。但是, 当MgCl3、CaCl3分子中的Xc配体变化时, 在Mg-Cla、Mg-Clb和Ca-Cla、Ca-Clb的键长变化规律为:MgF3(1.853 64 Ä)>MgF2Cl(1.814 35 Ä)>MgF2Br(1.811 85 Ä); CaF3(2.124 04 Ä)>CaF2Cl(2.093 63 Ä)>CaF2Br(2.089 16 Ä)。

可以看出, 当超卤素体系中的配体原子被半径更大的卤素配体取代后, 原卤素配体键长减小。因此可以总结出以下规律:

1) 当只存在一种配体时, 随着超卤素体系中卤素配体半径的变大, 键长增加;

2) 当存在多种配体时, 随着超卤素体系中被取代配体半径的变大, 原有配体键长减小。

此外, 为了更好地考察这些超卤素阴离子MX3-体系中键的特点, 在MP2/6-311+G(d)水平下进行了体系的自然键轨道(NBO)分析, 其NBO电荷列于表 2中。

表 2 超卤素阴离子MX3-的中心原子M及配体原子上的NBO电荷

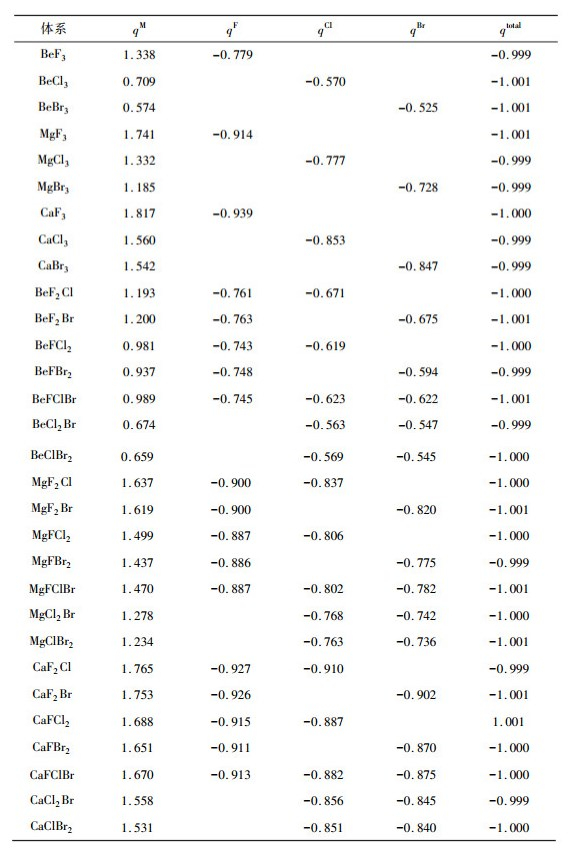从表 2中可以看出:随着键长的增加, 中心原子以及卤素配体中NBO电荷量均减小; 卤素配体的半径越大, 携带的NBO电荷越少。其原因可能是配体原子的电负性大小顺序是:F>Cl>Br。另外, 当中心原子是Be时, Be原子上的正电荷最高只有1.338, 配体原子上的负电荷最高只有0.779, 而每个超卤素分子总的NBO电荷为-1。所以卤素原子与Be中心原子之间是典型的共价键。进一步分析可知:当中心原子是Mg和Ca时, 配体原子和中心原子间同时存在离子键成分和共价键成分。

2.2 电离势

MX3-(M=Be, Mg, Ca; X=F, Cl, Br)体系的垂直电子电离能VIPn和VIPc分别在不同水平下(MP2和OVGF)计算得出并列于表 3中。VIPn值是采用MP2方法, 不改变中性分子的结构而结合一个电子所放出的能量。VIPc值是在阴离子平衡结构下用外层价电子格林函数法的计算结果。两种方法都是用相同的6-311+G(d)基组进行计算。

表 3 超卤素阴离子MX3-的垂直电子电离势(VIPn, VIPc)

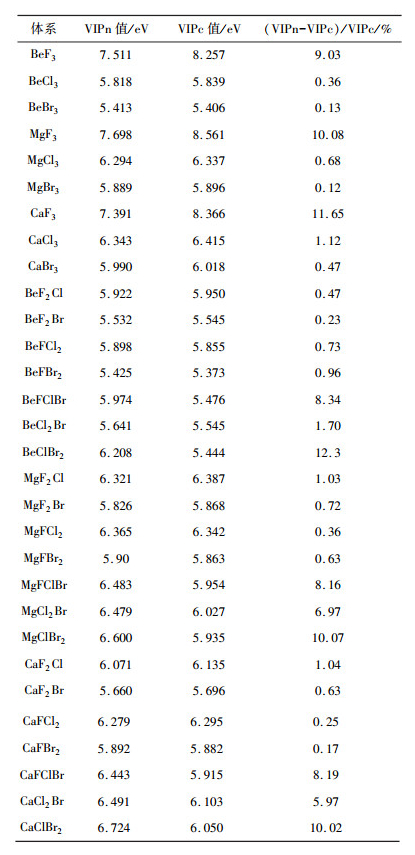此外, 将VIPn结果与VIPc结果之间的偏差定义为“(VIPn-VIPc)/VIPc”, 列在表 3中。可以清楚地看到这些偏差绝大多数分布在10%以内, 偏差很小, 因此可以确定使用OVGF方法计算阴离子的垂直电子电离势的精确性, 说明所选的理论方法对能量的测量是可靠的。

表 3中的计算结果表明:所有超卤素阴离子MX3-(M=Be, Mg, Ca; X=F, Cl, Br)的电离势IP都高于Cl原子的电子亲和势EA值(3.6 eV), 因此它们可以被视为超卤素。这意味着这些超卤素团簇拥有很高的电子亲和势, 很容易得到电子。根据表 3, 显而易见超卤素MX3-(M=Be, Mg, Ca; X=F, Cl, Br)的电离势受卤素配体原子的性质的影响很大。尺寸比较小的卤素配体原子可以导致其所在的体系具有更高的电离势, 例如:BeF3(7.511)>BeCl3(5.818)>BeBr3(5.413);BeF3(7.511)>BeF2Cl(5.922)>BeF2Br(5.532)。

3 结论

系统地理论预测出一种新型超卤素MX3(M=Be, Mg, Ca; X=F, Cl, Br)体系。它们的几何结构和能量性质也都通过计算得到并讨论。在MP2/6-311+G(d)水平下优化出的30种超卤素分子都是平面几何结构。配体与配体之间的相互作用增强了它们的稳定性。所有MX3分子的能隙值都非常大, 分别在8.70~14.00 eV之间, 如此大的能隙值证明了这些物质结构都是可以稳定存在的。为了保证MX3(M=Be, Mg, Ca; X=F, Cl, Br)体系的垂直电子电离势的计算结果的可靠性, 采用了两种方法:一是利用外层价电子格林函数法(OVGF)进行计算; 二是采用MP2方法, 不改变中性分子的结构, 计算结合一个电子所放出的能量。两种方法计算出的垂直电子电离能相近, 证明该理论计算方法是可靠的。通过计算和分析还发现, 超卤素体系中的卤素配体的原子尺寸可以影响超卤素的垂直电子电离能。尺寸比较小的卤素配体原子可以导致其所在的MX3体系具有更高的垂直电子电离能。

理论研究证明了可以通过改变超卤素中的配体来设计和合成一种具有很高电子亲和势的新型超卤素, 为将来选择不同配体、设计出更多的超卤素提供了理论依据。

参考文献
[1]
KHANNA S N, JENA P. Assembling crystals from clusters[J]. Phys.Rev.Lett, 1992, 69(11): 1664. DOI:10.1103/PhysRevLett.69.1664
[2]
BERGERON D E, CASTLEMAN A W, MORISATO T, et al. Formation of Al13I-:Evidence for the superhalogen character of Al13-I[J]. Science, 2004, 304(5667): 84-87. DOI:10.1126/science.1093902
[3]
BERGERON D E, ROACH P J, CASTLEMAN A W, et al. A1 cluster superatoms as halogens in polyhalides and as alkaline earths in iodide salts[J]. Science, 2005, 307(5707): 231-235. DOI:10.1126/science.1105820
[4]
GUTSEV G L, BOLDYREV A I. DVM-Xα calculations on the ionization potentials of MXk+1 complex anions and the electron affinities of MXk+1 "superhalogens"[J]. Journal of Chemical Physics, 1981, 56(3): 277-283.
[5]
WU C H, KUDOA H, IHLE H R. Thermochemical properties of gaseous Li3O and Li2O[J]. Journal of Chemical Physics, 1979, 70(4): 1815-1820. DOI:10.1063/1.437656
[6]
SCHLEYER P V R, WUERTHWEIN E U, POPLE J A. Effectively hypervalent first-row molecules.1.Octet rule violations by OLi3 and OLi4[J]. Journal of the American Chemical Society, 1982(104): 5839-5841.
[7]
REED A E, WEINSTOCK R B, WEINHOLD F. Natural population analysis[J]. Journal of Chemical Physics, 1985, 83(2): 735-746. DOI:10.1063/1.449486
[8]
WANG X B, DING C F, WANG L S, et al. First experimental photoelectron spectra of superhalogens and their theoretical interpretations[J]. Journal of Chemical Physics, 1999, 110(10): 4763-4771. DOI:10.1063/1.478386
[9]
FREZA S, SKURSKI P. Enormously large(approaching 14 eV!) electron binding energies of HnFn+1(n=1-5, 7, 9, 12)anions[J]. Chemical Physics Letters, 2010, 487(1): 19-23.
[10]
ANUSIEWEICZ I, SKURSKI P. Unusual structures of Mg2F5 superhalogen anion[J]. Chemical Physics Letters, 2007, 440(1-3): 41-44. DOI:10.1016/j.cplett.2007.04.016
[11]
FRISCH M J, TRUCKS G W, SCHLEGEL H B, et al.Gaussian 09[CP].Revision A02, Gaussia, Inc., Wallingford CT, 2009.
[12]
DENNINGTON R, KEITH T, MILLAM J.GaussView[CP].Version 5, Semichem Inc., Shawnee Mission, KS, 2009.
[13]
BECKE A D. Density-functional thermochemistry.Ⅲ.The role of exact exchange[J]. J.Chem.Phys, 1993, 98(7): 5648. DOI:10.1063/1.464913
[14]
MBLLER C, PLESSET M S. Note on an approximation treatment for many-electron systems[J]. Phys.Rev, 1934, 46: 618. DOI:10.1103/PhysRev.46.618
[15]
PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, molecules, solids, and surfaces:Applications of the generalized gradient approximation for exchange and correlation[J]. Phys.Rev.B, 1992, 46(11): 6671-6687. DOI:10.1103/PhysRevB.46.6671