| 复4D超混沌系统的镇定与同步问题 |
自1963年Lorenz首次发现混沌系统以来, 具有重要研究价值的热门方向是混沌系统及其现象[1]。状态变量属于复空间的复混沌系统是另一种重要的混沌动力系统[2-3]。它在定理和应用上得到了广泛的研究, 成为近年来的热门话题之一。特别是由于复混沌系统是由实数和虚数组成的, 它比实混沌系统具有更好的加密效果[4-5]。由于复混沌系统的动力学行为比实混沌系统更为复杂, 因此研究此类系统的控制问题非常困难。
传统的线性反馈控制器虽然结构简单, 物理上易于实现, 但也存在过分依赖控制反馈增益值的问题, 极大地限制了系统初始值设定的自由度[6-8]。目前, 大多数研究人员采用以下方法:首先, 通过分离复状态变量的实部和虚部, 将复混沌系统转化为其等价的实混沌系统, 然后为被控制的实混沌系统设计相应的控制器, 最后根据复混沌与其等价实混沌系统之间的对应关系, 得到复混沌系统的对应控制器, 从而实现对这类复混沌系统的控制问题[9-10]。但是, 这种方法也存在一些问题:一方面, 第一步缺乏系统的方法, 即对于特定的复混沌系统, 如何找到系统的方法将复混沌系统转化为与其等价的实混沌系统, 不仅具有重要的理论意义, 而且具有广泛的应用价值[11-12];另一方面, 前人设计的控制器大多是复杂[13-15];因此, 它们很难在实际情况中应用[16-18]。关于求解非线性系统的控制问题, 物理学上也有控制器可供选择, 动态增益反馈控制器为就是其中之一[19]。
本文的主要贡献是利用动态反馈控制方法为复4D超混沌系统设计了几个物理控制器。与以往的研究成果相比, 这种控制器将更为简单, 并可以实现复4D超混沌系统的稳定和完全同步。最后通过Matlab进行数值模拟, 模拟结果验证了理论结果的正确性和有效性。
1 理论准备考虑如下混沌系统:
| $ f(x)=\dot{x}, $ | (1) |
其中,
设系统(1)为主系统, 则相应的受控从系统为:
| $ \dot{e}=f(y)-f(x)+\boldsymbol{B} u, $ | (2) |
其中,
令e=y-x, 则可以得到误差系统如下所示:
| $ \dot{e}=\boldsymbol{f}(y)-\boldsymbol{f}(x)+\boldsymbol{B} u, $ | (3) |
其中,
一个复4D超混沌系统, 系统中的每个方程都有一个三项叉积, 表示为
| $ \left\{\begin{array}{l} \dot{m}=a(m-n)+n p q \\ \dot{n}=b(m+n)-m p q \\ \dot{p}=\frac{1}{2}(\overline{m n}+m\;\bar{n}) q-c p, \\ \dot{q}=\frac{1}{2}(\overline{m}n+m\;\bar{n}) p-d q \end{array}\right. $ | (4) |
其中, a、b、c、d都是正的实常数参数, m和n是复变量, p和q是实变量, ·代表关于时间的导数, -代表复共轭变量且
令m=x1+ix2, n=x3+ix4, p=x5, q=x6, 则系统(4)可以转化为以下等价的实系统
| $ \dot{x}=\boldsymbol{f}(x)=\left\{\begin{array}{l} a\left(x_3-x_1\right)+x_3 x_5 x_6 \\ a\left(x_4-x_2\right)+x_4 x_5 x_6 \\ b\left(x_1+x_3\right)+x_1 x_5 x_6 \\ b\left(x_2+x_4\right)+x_2 x_5 x_6 \\ \left(x_1 x_3+x_2 x_4\right) x_6-c x_5 \\ \left(x_1 x_3+x_2 x_4\right) x_5-d x_6 \end{array}\right., $ | (5) |
其中,
设系统(5)为主系统, 则相应的受控从系统为:
| $ \dot{y}=\boldsymbol{f}(y)+\boldsymbol{B} u, $ | (6) |
其中,
| $ \boldsymbol{B}=\left(\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right)。$ |
在本节中, 我们通过动态反馈增益的方法来实现复4D超混沌系统的镇定和同步问题。
定理3.1 考虑系统(6), 如果被设计的控制器u是
| $ u=k_1(t) \boldsymbol{B}^{\mathrm{T}} y, $ | (7) |
其中
| $ \dot{k}_1=-|| y||^2, $ | (8) |
说明系统(6)实现了镇定。
证明:令x3=x4=x5=0, 则相应的三维子系统为
| $ \left\{\begin{array}{l} \dot{x}_1=-20 x_1 \\ \dot{x}_2=-20 x_{2} \\ \dot{x}_6=-2 x_6 \end{array}\right. 。$ | (9) |
是渐进稳定的。因此, (f(y), B)是可控的, 这就完成了证明。
定理3.2 考虑主系统(5)和从系统(6), 如果被设计的控制器u是
| $ u=k_1(t) \boldsymbol{B}^{\mathrm{T}} e, $ | (10) |
其中e=y-x,
| $ \dot{k}_1=-|| e||^2, $ | (11) |
说明主系统(5)和从系统(6)实现了完全同步。
证明:令e=y-x, 则误差系统为
| $ \dot{e}=\boldsymbol{G}(x, e)+\boldsymbol{B} u, $ | (12) |
其中
| $ \boldsymbol{G}(x, e)=\left(\begin{array}{l} a\left(e_3-e_1\right)+\left(y_3 y_5 y_6-x_3 x_5 x_6\right) \\ a\left(e_4-e_2\right)+\left(y_4 y_5 y_6-x_4 x_5 x_6\right) \\ b\left(e_1+e_3\right)-\left(y_1 y_5 y_6-x_1 x_5 x_6\right) \\ b\left(e_2+e_4\right)-\left(y_2 y_5 y_6-x_2 x_5 x_6\right) \\ G_5(x, e) \\ G_6(x, e) \end{array}\right), $ | (13) |
其中:
| $ G_5(x, e)=\left(y_1 y_3 y_6-x_1 x_3 x_6\right)+\left(y_2 y_4 y_6-x_2 x_4 x_6\right)-c e_5, $ | (14) |
| $ G_6(x, e)=\left(y_1 y_3 y_5-x_1 x_3 x_5\right)+\left(y_2 y_4 y_5-x_2 x_4 x_5\right)-d e_6, $ | (15) |
显然, 如果e3=e4=e5=0, 且a=20, b=10, c=1, b=2, 则相应的三维误差系统为
| $ \left\{\begin{array}{l} \dot{e}_1=-20 e_1+x_1 x_3 x_6 \\ \dot{e}_2=-20 e_2+x_4 x_5 x_6 \\ \dot{e}_6=x_3 x_5 e_1+x_4 x_5 e_2-2 e_6 \end{array}\right., $ | (16) |
是渐进稳定的。因此, (G(x, e), B)是可控的, 这就完成了证明。
4 数值仿真受控复4D超混沌系统的初始值为x(0)=[1, 1, 2, 2, 3, 3, -1], 动态反馈增益k(t)的初始值k(0)=-1, 仿真结果如下图所示。从图 1和图 2中可以看出复4D超混沌系统的每个状态变量是渐进稳定的, 图 3表明动态反馈增益k(t)收敛到一个合适的常数。
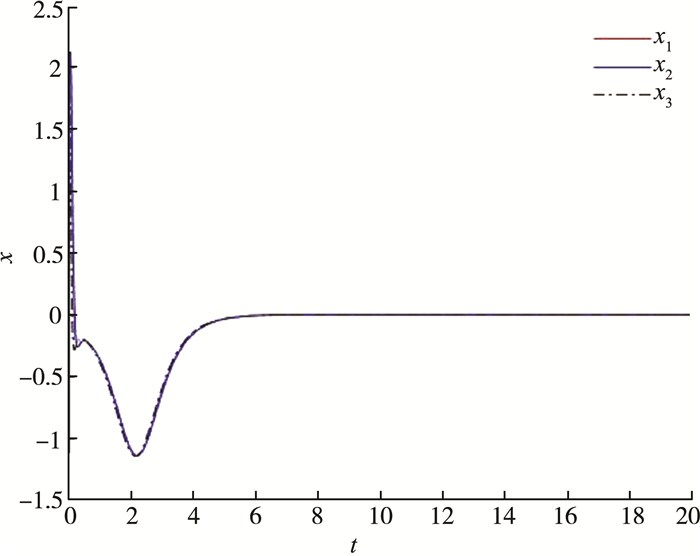 |
| 图 1 状态变量x1、x2、x3渐进稳定 |
 |
| 图 2 状态变量x4、x5、x6渐进稳定 |
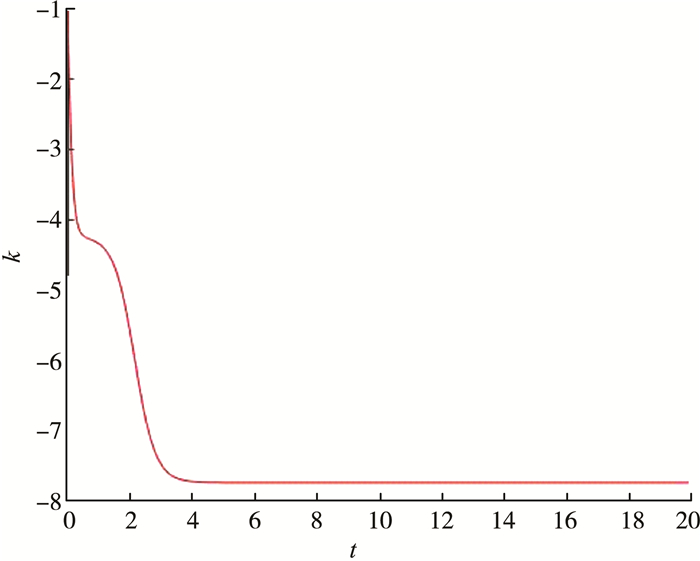 |
| 图 3 动态反馈增益收敛到一个合适的常数 |
主系统的初始值x(0)=[-1, -2, 3, 2, -1, 2], 从系统的初始值y(0)=[3, 2, -1, -2, 3, -2], 动态增益反馈k(t)的初始值k(0)=-1。仿真结果如下图所示。从图 4和图 5中可以看出控制器被激活时的误差系统, 表明已经稳定, 这意味着复4D超混沌系统中完全同步已经实现。图 6和图 7显示了控制器启动时状态变量的动态变化, 主系统和从系统的状态实现了完全同步, 图 8表明动态反馈增益k(t)收敛到一个负常数。
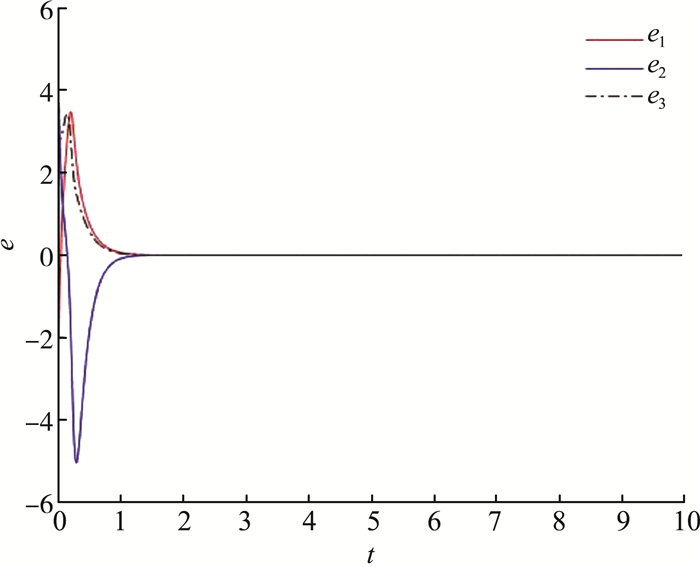 |
| 图 4 误差系统e1、e2、e3渐进稳定 |
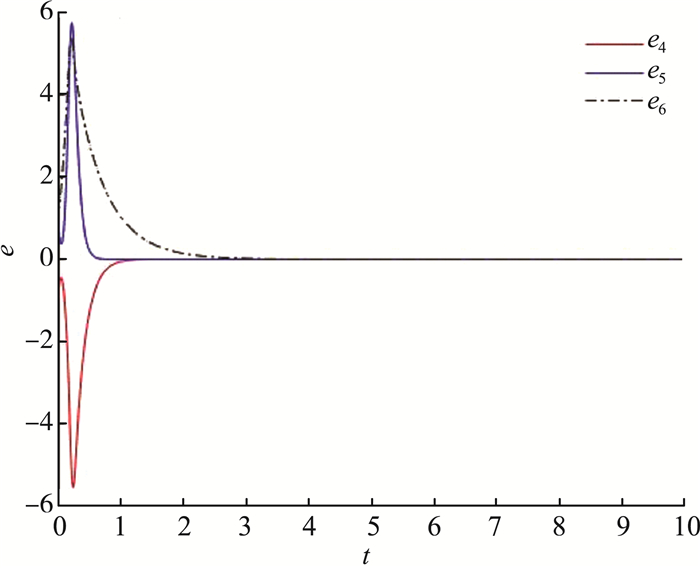 |
| 图 5 误差系统e4、e5、e6渐进稳定 |
 |
| 图 6 主系统x1、x2、x3和从系统y1、y2、y3的状态实现了完全同步 |
 |
| 图 7 主系统x4、x5、x6和从系统y4、y5、y6的状态实现了完全同步 |
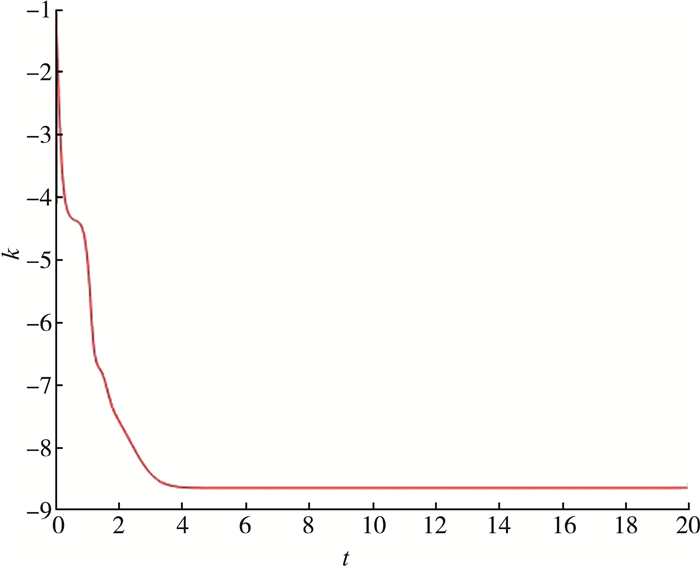 |
| 图 8 动态反馈增益收敛到一个合适的负常数 |
5 结论
本文研究了通过动态增益反馈控制的方法来实现复4D超混沌系统的镇定和同步问题。首先, 通过分离复变量的实部和虚部, 将复4D超混沌系统转化为等价的六维实系统。然后, 设计两个简单的控制器来实现复4D超混沌系统的镇定和同步问题。最后, 通过Matlab进行数值仿真验证了理论结果的正确性和有效性。本文提出的研究方法也可以应用于其他混沌或超混沌系统。
| [1] |
戴先中, 刘海国. 两变频调速电机系统[J]. 电网技术, 2001, 25(8): 18-22. |
| [2] |
郭荣伟. 混沌系统的控制问题研究及其应用[M]. 北京: 科学出版社, 2020.
|
| [3] |
衣晓峰. 一类复混沌系统的控制问题研究[D]. 济南: 齐鲁工业大学, 2020.
|
| [4] |
祝大伟, 涂俐兰. 随机扰动下Lorenz混沌系统的自适应同步与参数识别[J]. 物理学报, 2013, 62(5): 106-111. |
| [5] |
AVIRAM I, RABINOVITCH A. Bifurcation analysis of bacteria and bacteriophage coexistence in the presence of bacterial debris[J]. Communications on Nonlinear Science and Numerical Simulations, 2012, 17: 242-254. DOI:10.1016/j.cnsns.2011.04.031 |
| [6] |
HUANG C, CAO J. Active control strategy for synchronization and anti-synchronization of a fractional chaotic financial system[J]. Physica A, 2017, 4731(5): 262-275. |
| [7] |
LIU D, ZHU S, SUN K. Anti-synchronization of complex-valued memristor-based delayed neural networks[J]. Neural Networks, 2018, 105(9): 1-13. |
| [8] |
JIA B, WU Y, HE D, et al. Dynamics of transitions from anti-phase to multiple in-phase synchronizations in inhibitory coupled bursting neurons[J]. Nonlinear Dynamics, 2018, 93: 1599-1618. DOI:10.1007/s11071-018-4279-x |
| [9] |
REN L, GUO R W. A necessary and sufficient condition of anti-synchronization for chaotic systems and its applications[J]. Math.Problem.Eng, 2015, 434651: 1-7. |
| [10] |
MAHMOUD E E. Control and synchronization of a new chaotic model with complex variables and cubic nonlinear terms[J]. Results in Physics, 2017(10): 1346-1356. |
| [11] |
刘延涛, 刘恒. 时空混沌与Li-Yorke敏感[J]. 大连民族学院学报, 2008, 10(5): 106-111. |
| [12] |
马会泉. 混沌系统的同步研究[D]. 天津: 河北工业大学, 2001.
|
| [13] |
李农, 李建芬. 混沌系统的统一投影同步[J]. 物理学报, 2011, 60(11): 110512. |
| [14] |
顾谋华. 混沌系统的几种控制方法及其应用研究[D]. 南京: 南京理工大学, 2009.
|
| [15] |
过榴晓. 混沌系统的广义同步及动态网络同步研究[D]. 无锡: 江南大学, 2009.
|
| [16] |
陈关荣, 吕金虎. Lorenz系统的动力学分析、混沌控制与同步[M]. 北京: 科学出版社, 2003.
|
| [17] |
李玥, 张之光. 超混沌数字电路在数字供应链中的应用[J]. 数字技术与应用, 2016(12): 96-105. |
| [18] |
黄秋灵. 离散动力系统的混沌理论及其应用[D]. 济南: 山东大学, 2012.
|
| [19] |
YI X, GUO R W. Stabilization of chaotic systems with both uncertainty and disturbance by the UDE-Based control method[J]. IEEE Access, 2020(8): 62471-62477. |
 2022, Vol. 36
2022, Vol. 36


