| 小波变换在电力系统故障检测中的应用 |
2. 齐鲁理工学院 机电工程学院,济南 250200
2. Mechanical and Electrical Engineering, Qilu Institute of Technology, Jinan 250200, China
电力系统的迅猛发展使得电压等级逐渐增高, 输电线路日益复杂, 对于电力系统故障的检测也越来越困难, 然而电力系统发生故障会对企业、单位的正常运转和国民生产生活造成严重的影响, 因此, 实现电力系统故障的精准定位尤为关键[1]。
传统的故障检测方法是基于傅里叶变换进行的, 然而傅里叶变换不具备时域局部化分析能力, 小波变换是在傅里叶变换基础上的进一步完备和拓展, 解决了傅里叶变换在处理非平稳信号时无法表述信号时频局部化性质的不足, 不仅具备良好的波形整体分析能力, 还具备出众的时频域的局部化分析能力, 能够有效的获取信号在时域与频域部分的细节信息, 具有判断信号奇异点位置以及分析奇异程度强弱的能力[2]。因此, 采用小波变换分析电力系统故障问题具有非常重要的意义。
1 小波变换 1.1 小波变换理论小波变换是信号与时-频窗口可自适应变化的小波基函数卷积运算, 将信号分解为处在不同频率带-时间段的各个部分的过程[3]。将任意L2(R)空间内的信号f(t)在具有伸缩-平移性的ψa, b(t)下展开, 称这种分解f(t)的过程为连续小波变换(Continuous Wavelet Transform, CWT), 表达式为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {W_f}(a,b) = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \langle f,{\psi _{a,b}}\rangle {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = |a{|^{ - 1/2}}\mathop \smallint \nolimits_{ - \infty }^{ + \infty } \\ f(t)\overline {\psi (\frac{{t - b}}{a})} dt \end{array} $ | (1) |
其中:ψa, b(t)为母小波函数, a是尺度系数, b是平移系数。小波变换的实质是采用不同的滤波器对信号滤波, 在高频区域内, 高分辨率体现在时间方面, 低频区域内, 高分辨率体现在频率方面[4]。
实际工程中提取到的信号常常为离散信号, 针对尺度因子a和平移因子b离散化ψa, b(t):
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _{j,k}}(t) = {a_0}^{ - j/2}\psi (\frac{{t - k{a_0}^j{b_0}}}{{{a_0}^j}}) = \\ {a_0}^{ - j/2}\psi ({a_0}^{ - j}t - k{b_0}) \end{array} $ | (2) |
进一步得到离散小波变换(DWT):
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{j,k}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \langle f,{\psi _{j,k}}\rangle {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {a_0}^{ - j/2}\mathop \smallint \nolimits_{ - \infty }^{ + \infty } \\ f(t)\overline {\psi ({a_0}^{ - j}t - k{b_0})} dt \end{array} $ | (3) |
在一定条件下离散小波系数Cj, k可完全特征化f。
1.2 小波的Mallat算法1) 分解算法
对于f(t)∈L2(R), 其频谱为f(ω), 然而实际工程中的频谱是有限的, 只要选择足够大的j使得f(t)∈Vj+1, f(t)就可用Vj+1展开:
| $ f(t) = \sum\limits_n {{c_{j + 1,n}}} {\varphi _{j + 1,l}}(t) $ | (4) |
式中, cj+1, n为尺度空间Vj+1的尺度系数, cj+1, n=〈f, φj+1, n〉, φj+1, k(t)为尺度空间Vj+1的尺度函数。
由于Vj+1=Vj⊕Wj, 即Vj⊥Wj, 进而:
| $ f(t) = \sum\limits_n {{c_{j,k}}} {\varphi _{j,k}}(t) + \sum\limits_k {{d_{j,k}}} {\varPsi _{j,k}}(t) $ | (5) |
式中
| $ {{c_{j,k}} = \langle f,{\varphi _{j,k}}\rangle = \sum\limits_n {{c_{j + 1,n}}} {{\bar h}_{j - 2k}}} $ | (6) |
| $ {{d_{j,k}} = \langle f,{\varPsi _{j,k}}\rangle = \sum\limits_n {{c_{j + 1,n}}} {{\bar g}_{j - 2k}}} $ | (7) |
由上式可知, 可由大的空间Vj+1中的系数cj+1, k得到小的子空间Vj和Wj中的系数cj, k, dj, k。分解过程如图 1所示。
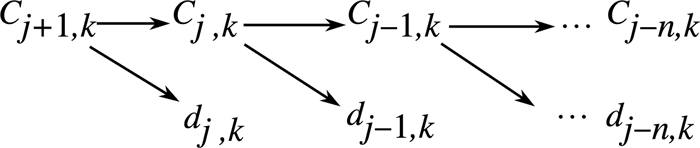 |
| 图 1 Mallat分解过程 |
2) 重构算法
Mallat重构算法实质是分解算法的逆运算, 式(6)、(7)代入式(5), 整理得到:
| $ \begin{array}{*{20}{l}} {f(t) = \sum\limits_k {{c_{j,k}}} (\sum\limits_l {{h_{l - 2k}}} {\varphi _{j + 1,l}}(t)) + }\\ {\sum\limits_k {{d_{j,k}}} (\sum\limits_l {{g_{l - 2k}}} {\varphi _{j + 1,l}}(t))}\\ { = \sum\limits_l {(\sum\limits_k {{c_{j,k}}} {h_{l - 2k}} + \sum\limits_k {{d_{j,k}}} {g_{l - 2k}})} {\varphi _{j + 1,l}}(t)} \end{array} $ | (8) |
l→k, k→n, 进一步得到:
| $ {c_{j + 1,k}} = \sum\limits_n {{c_{j,n}}} {h_{k - 2n}} + \sum\limits_n {{d_{j,n}}} {g_{k - 2n}} $ | (9) |
由(9)式可见, 重构是由小的子空间Vj和Wj中的展开系数cj, k和dj, k计算大的子空间Vj+1中的系数cj+1, k, 重构过程如图 2所示。
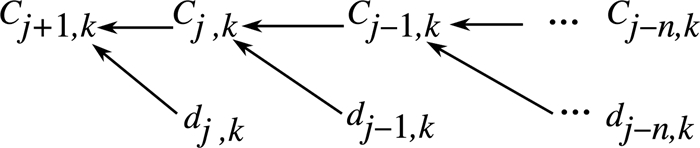 |
| 图 2 Mallat重构过程 |
2 奇异信号的模极大值检测原理
信号存在奇异性是由于原信号的某点不连续或者其某阶微分存在间断点。奇异性检测的实质是辨识出信号的奇异点并分析信号畸变程度的过程, 利用小波变换时频局部化的性质, 可以有效的对信号奇异性进行分析[5-6]。
Wf(s, u)为点u处尺度为s的小波变换, 如果点u0附近的每一点u都满足:|Wf(s, u)|≤|Wf(s, u0)|, 则点u0就是|Wf(s, u)|在尺度s下的极大值点, |Wf(s, u0)|是小波变换模极大值[7]。不同尺度上的信号都会存在不同的模极大值, 因此, 可以通过提取信号中的模极大值点分析信号的奇异性, 模极大值检测的实质为基于多尺度分析的边缘检测, 对不同尺度的信号构造平滑函数进行光滑处理, 对信号平滑处理后, 取一、二阶微分识别出信号的奇异点[8]。
平滑函数为满足
| $ {{W^1}f(s,t) = f * {\psi _s}^{(1)}} $ | (10) |
| $ {{W^2}f(s,t) = f * {\psi _s}^{(2)}} $ | (11) |
将上式展开:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {W^1}f(s,t) = < f,{\psi _s}^{(1)} > = f * (s\frac{{d{\theta _s}}}{{dt}})(t) = \\ s\frac{d}{{dt}}(f * {\theta _s})(t) \end{array} $ | (12) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {W^2}f(s,t) < = f,{\psi _s}^{(2)} > = f * ({s^2}\frac{{{d^2}{\theta _s}}}{{d{t^2}}})(t) = \\ {s^2}\frac{{{d^2}}}{{d{t^2}}}(f * {\theta _s})(t) \end{array} $ | (13) |
信号f(t)在θ(t)的平滑作用下取一、二阶微分得到小波变换W1f(s, t)、W2f(s, t), f(t)的突变点经W1f(s, t)、W2f(s, t)处理后分别对应小波变换模的极值点和零点[9]。信号传输过程中非故障点的电气量会出现扰动, 易对过零点检测的准确性产生干扰, 并且过零点检测到的结果通常并不是突变点, 而是信号在慢区间的拐点, 因此根据极值点检测奇异信号比根据过零点更加可靠[10]。通过小波变换, 信号f(t)的突变点在W1f(s, t)上对应着极大值, 而在W2f(s, t)为过零点; 由小波变换Wf(s, t)的定义可知, |Wf(s, t) |的极大值点体现了f*θs(t)奇异点的位置, 因此通过检测|Wf(s, t)|极大值点可判断信号在不同尺度下的奇异点。
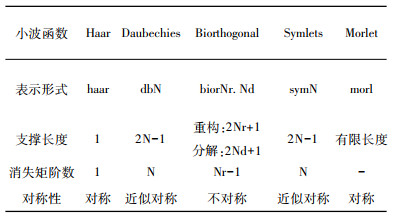
3 基于db4的故障信号检测算法 3.1 小波函数的选择不同小波函数的变换特性存在一定的差异性, 选取的母小波不同, 经小波变换后的小波系数也不尽相同, 因此, 在利用MATLAB进行仿真分析前, 先选取合适的母小波函数, 在小波函数的选择上需要兼顾其消失矩、对称性以及紧支撑性(支撑长度), 紧支撑性与消失矩决定了小波函数在特定尺度与平移下的影响范围, 因此在选择较小的支撑长度与较高阶的消失矩时需要折中处理, 对称性描述了小波重构后信号的平滑程度[11-12]。常见的小波函数及特性如表 1所示:
| 表 1 常见的小波函数及特性 |
 |
为了进一步分析不同小波对间断点的检测效果, 构造一个在t∈[0, 500]范围内为低频正弦信号、t∈[500, 1 000]范围内加入高频特征的freqbrk信号, 采用3种不同的小波:haar小波、sym4小波、db4小波对其分析, 分析结果如图 3所示, 结果表明这三种小波均可检测到信号间断点, 但明显db4小波效果更佳, 因此本文采用紧支撑性、对称性及消失矩良好的db4小波检测信号的奇异性。
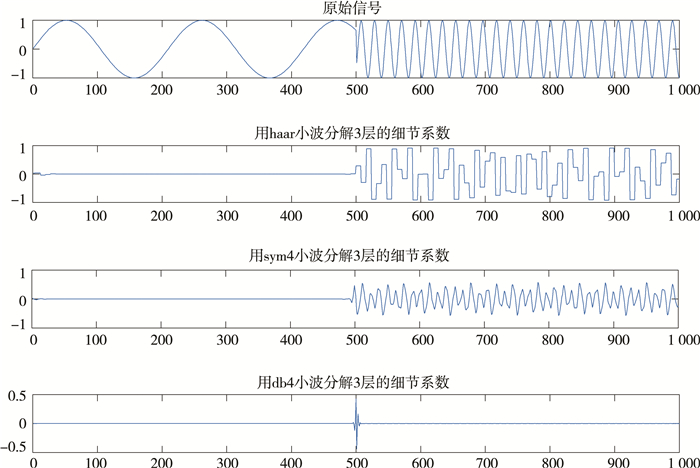 |
| 图 3 不同小波间断点检测对比 |
3.2 算法步骤
结合故障信号的特性, 提出一种利用db4小波对故障进行诊断算法, 具体如下:
1) 利用Simulink建立电力系统模型, 输出故障信号;
2) 选择母小波db4, 确定分解、重构层数以及阈值T;
3) 利用FFT和CWT对信号f分析, 对比处理结果;
4) 基于db4小波, 对模型输出的故障信号f进行分解和重构, 获得各层小波系数:W1f(k)、W2f(k)、…、Wjf(k);
5) 分析[Wjf(k)], j=1, 2, …, J模极大值情况, 判别有无故障出现;
6) 提取部分采样点db4小波分解细节系数, 确定模极大值点, 计算与实际故障点之间的误差。
4 建模与仿真 4.1 电力系统模型搭建本文通过MATLAB/simulink搭建了一个电压等级为220 kV, 工频50 Hz的电力系统仿真模型, 如图 4所示, 系统为双电源三相供电系统, 由输电线路、电压测量元件、电流测量元件、示波器、负载和故障发生器组成, 两电源三相相位相角均为30°, 采样频率20 KHz, 仿真时长T=0.15 s, 设置3 000个采样点; 该系统可模拟电力系统中可能出现的各种故障, 本文在t0=0.07 s处设置一个电力系统中易发生的单相接地故障, t1=0.12 s时恢复正常, 利用fourier变换和db4小波变换对比分析。
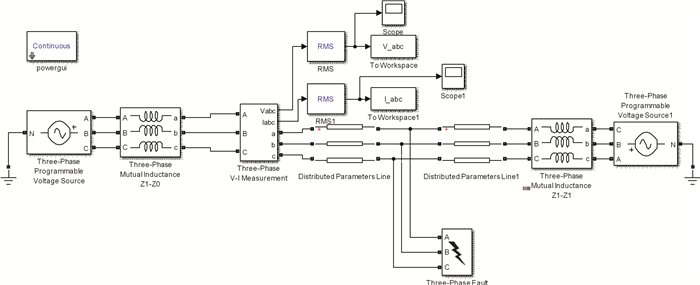 |
| 图 4 电力系统仿真模型 |
模型线路参数为:
| $ \begin{array}{*{20}{l}} {{R_0} = 0.427{\kern 1pt} {\kern 1pt} {\kern 1pt} \Omega /{\rm{km}},{L_0} = 3.961 \times {{10}^{ - 3}}{\rm{H}}/{\rm{km,}}}\\ {{C_0} = 7.25 \times {{10}^{ - 9}}{\rm{F}}/{\rm{km}},{R_1} = 0.183{\kern 1pt} {\kern 1pt} {\kern 1pt} \Omega /{\rm{km,}}}\\ {{L_1} = 8.63 \times {{10}^{ - 4}}{\rm{H}}/{\rm{km}},{C_1} = 1.63 \times {{10}^{ - 8}}{\rm{F}}/{\rm{km}}} \end{array} $ |
1) 仿真信号的提取
设置“Three-Phase Fault”相关参数, 通过Scope和Scope1可分别提取到系统运行时的电压波形和电流波形, 本文对稳定性更高的电压波形进行仿真分析, 系统正常工作时和故障发生时的电压波形如图 5所示。
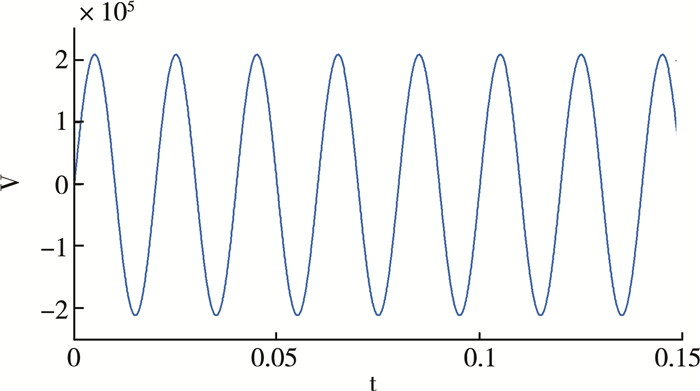 |
| 图 5 正常运行时的电压波形 |
对比图 5和图 6可知:正常运行时, 波形为频率、相位、幅值恒定的标准正弦波, “Three-Phase Fault”工作时, 线路发生故障, 电压波形出现了突变, 因此, 对Scope提取到的图 6所示波形做进一步分析。
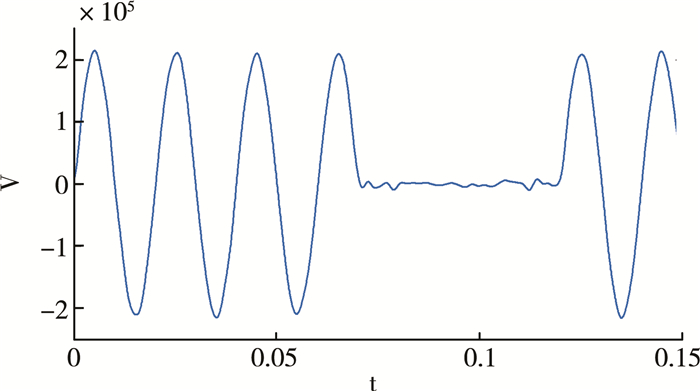 |
| 图 6 发生故障时的电压波形 |
2) 结果分析
为了确定图 6所示信号突变点的时间, 对信号分别作基于Daubechies 4小波的小波连续变换和Fourier变换, 并对仿真结果的可靠性对比分析。
由图 7可看出, 经FFT变换后的信号完全体现在了频率域中, 不具备时间尺度分析能力, 由于信号的奇异性需要在时域中分析处理, 因此Fourier变换不具备故障信号诊断的能力。图 8所示信号为对小波系数各层细节部分重构之后的波形, 使用紧支性、正则性、对称性及消失矩良好的db4小波对信号4层小波分解, 提取细节部分, 并重构1-4层信号, 根据小波分解的第一层高频信号d1能够非常有效的识别出系统故障信号中的突变成分, 故障信号经小波变换, 其细节部分在1 400采样点以及2 400采样点附近剧烈震荡, 是|Wf(s, k)|的极大值点, 即信号在采样处理后的奇异点, 由此断定系统发生了故障。
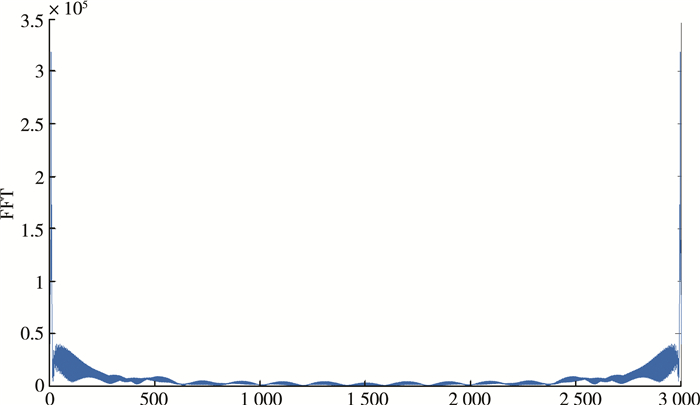 |
| 图 7 Fourier变换后的信号 |
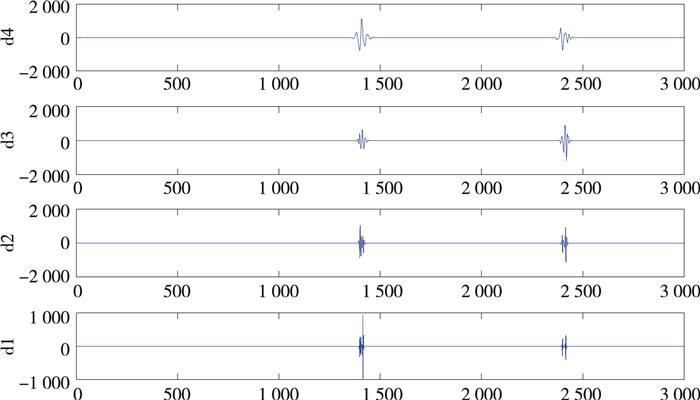 |
| 图 8 小波分解的各层细节系数 |
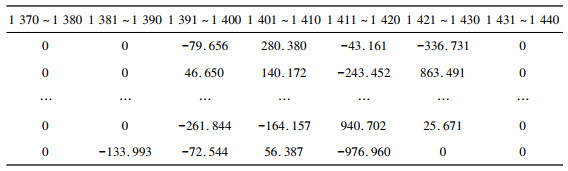
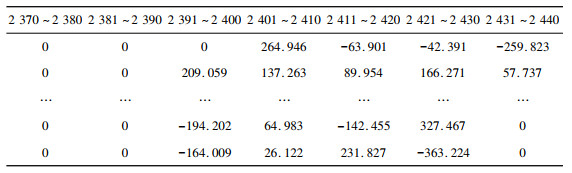
为了验证数据的真实性, 提取1 370~1 440采样点以及2 370~2 440采样点的db4小波分解第1层高频小波系数, 如表 2、表 3所示, 表 2数据表明故障发生时刻小波系数在1 390点表现出奇异性, 在1 429点恢复正常, 表 3数据表明故障恢复时刻小波系数在2 392点表现出奇异性, 在2 432点恢复正常。根据采样总点数以及仿真时间T得出故障发生时间t=
| 表 2 1 370~1 440采样点高频小波系数 |
 |
| 表 3 2 370~2 440采样点高频小波系数 |
 |
实际工程应用中, 可通过小波变换分析检测暂态行波波头到达母线测量点的时间以及反射行波首次到达测量点的时间, 利用行波两次传播到监测点的时间差对故障点精确定位[13], 如图 9所示, 当F点发生故障时, 暂态行波沿着输电线路向两侧传播, 以单端行波测距为例, 母线监测点检测到的故障行波首次到达M侧的时间为Tm1、经反射再次到达M侧的时间为Tm2, 利用此时间差Δt以及行波传播速度
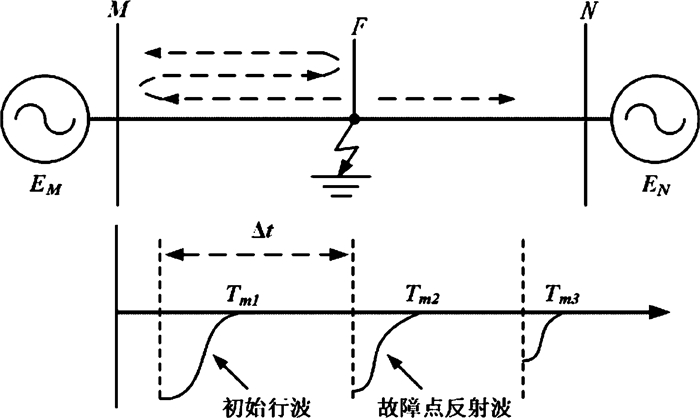 |
| 图 9 故障测距示意图 |
5 结论
本文以MATLAB/Simulink搭建的电力系统模型输出的故障数据为基础, 给出了一种利用小波变换检测故障点的方法。由于不同小波函数的变换特性存在一定的差异性, 经过分析, 提出通过db4小波进行检测的方法以获得更为准确的结果。对故障信号经过多分辨率小波分解后, 通过分析各重构信号, 发现故障信号的能量在各小波系数上的分布是不同的, 信号有价值的部分主要体现在特定的小波系数上, 利用这些模极大值点的数据, 可以有效的确定信号奇异性发生的位置, 误差仅为0.71%, 对一些系统的实时故障检测提供了有利的探索方法, 有着广泛深远的应用前景。
| [1] |
谢小荣, 王银, 刘华坤, 等. 电力系统次同步和超同步谐波相量的检测方法[J]. 电力系统自动化, 2016, 40(21): 189-194. DOI:10.7500/AEPS20160104002 |
| [2] |
ZHANG Z X, LIU X, PIAO Z L. Fault line detection in neutral point ineffectively grounding power system based on phase-locked loop[J]. IET Generation Transmission & Distribution, 2014, 8(2): 273-280. |
| [3] |
王建元, 张苛, 宋月航. 基于双树复小波与分形维数的配电网选线研究[J]. 吉林电力, 2020, 48(01): 16-19, 50. DOI:10.3969/j.issn.1009-5306.2020.01.005 |
| [4] |
张昊, 赵洋, 赵晓红. 基于小波分析的网络通信大数据谱聚类算法研究[J]. 自动化与仪器仪表, 2020(01): 36-39, 43. |
| [5] |
唐炬, 董玉林, 樊雷, 等. 基于Hankel矩阵的复小波-奇异值分解法提取局部放电特征信息[J]. 中国电机工程学报, 2015, 35(07): 1808-1817. |
| [6] |
REZA M S, AGELIDIS G. A robust technique for single phase grid voltage fundamental and harmonic parameter estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(12): 3262-3273. DOI:10.1109/TIM.2015.2444259 |
| [7] |
张江林, 张亚超, 洪居华. 基于离散小波变换和模糊K-modes的负荷聚类算法[J]. 电力自动化设备, 2019, 39(02): 100-106, 122. |
| [8] |
王秋生, 陈璐, 袁海文, 等. 基于经验小波变换的电晕电流降噪方法[J]. 电网技术, 2017, 41(02): 670-676. |
| [9] |
李章勇, 姜瑜, 王伟. 基于小波变换的皮电信号滤波及奇异性检测[J]. 科学技术与工程, 2013, 13(04): 1118-1122. DOI:10.3969/j.issn.1671-1815.2013.04.060 |
| [10] |
SHEN X, HAN Y, ZHU S, et al. Comprehensive power-supply planning for active distribution system considering cooling, heating and power load balance[J]. Journal of Modern Power Systems & Clean Energy, 2015, 3(4): 485-493. |
| [11] |
曹玲芝, 李振杰. 基于dq变换与小波多分辨率分析的电力系统暂态复合扰动信号检测方法[J]. 电力系统保护与控制, 2016, 44(21): 138-143. DOI:10.7667/PSPC151848 |
| [12] |
周龙华, 付青, 余世杰, 等. 基于小波变换的谐波检测技术[J]. 电力系统及其自动化学报, 2010, 22(1): 80-85. DOI:10.3969/j.issn.1003-8930.2010.01.015 |
| [13] |
李国庆, 王丹, 姜涛, 等. 基于递归连续小波变换的电力系统振荡模式辨识[J]. 电力自动化设备, 2016, 36(09): 8-16. |
 2020, Vol. 34
2020, Vol. 34


