| 实半正定矩阵秩约束锥的若干性质 |
在输出反馈和鲁棒控制[1-2]、组合优化[3]、矩阵补全[4]、系统模型降阶[5-7]、图形图像处理[8-9]等问题中,通常可以把原问题转化为一个带有实半正定矩阵秩约束的模型来求解。但是该模型的引入直接带来了两个问题:一是秩约束的可行域究竟是什么样的,它有什么样的几何结构与性质;二是由于秩约束为一个非凸不可微约束,使得转化后优化问题的求解变得比较复杂,经典的求解优化问题的方法不再能用来直接求解该模型,所以研究如何逼近该非凸的秩约束优化问题的求解是必要的。第二个问题是近年来的研究热点。常用的方法是用凸函数约束或者其他方法去逼近秩约束,得到了一些比较好的结果[10-12]。这些结果主要集中在对于秩函数的逼近函数研究上,而对该秩约束的可行域的结构与分析性质等却少有研究[13-15]。本文对这个问题进行了初步研究,得到一些结论。这些结论对于进一步深刻了解秩约束的性质以及如何逼近该约束具有一定的意义。
采用符号如下:矩阵A∈Sn×n表示矩阵A为n×n的对称矩阵,A≥0(或>0)表示A为半正定(或正定)矩阵,矩阵A∈Sn×n表示矩阵A为n×n的对称矩阵,A≥0(或>0)表示A为半正定(或正定)矩阵。
1 定义与引理定义1:锥。K为一集合,x0∈K,若x∈K, λ>0, x0+λ(x-x0)∈K,称K为以x0为顶点的锥。特别当x0=0时,K表示以0为顶点的锥,且λK⊂K,即此时锥对正数乘法封闭。
定义2:凸锥。若K为锥,且∀x1, x2∈K, λ1, λ2>0,有λ1x1+λ2x2∈K,则称K为凸锥。即凸锥对正数加法和正数乘法封闭。
定义3:凸锥的边界。若凸锥中的任意点都存在一个小邻域,使得该邻域内既有属于凸锥K的点,也有不属于凸锥K的点,则称该点集为凸锥K的边界,记为∂K。
定义4:共轭锥。设为K凸锥,则K*={x*|〈x, x*〉≥0, x∈K}称为K的共轭凸锥。显然,凸锥的共轭锥K*也是凸锥。
下面先考虑集合B(r)={A∈Sn×n|A≥0, rank(A)=r}的性质。
引理1:当r=n时,集合B(n)={A∈Sn×n|A>0, rank(A)=n}为不包含原点的一个凸集。
证明:由B(n)的定义,0矩阵不属于B(n),且不存在矩阵A0∈B(n),使得对任意的正定矩阵A∈B(n), A0+λ(A-A0)>0, ∀λ>0,所以B(n)不是锥;另一方面,假设A1, A2∈B(n),λ1, λ2>0,根据矩阵的正定性可知,λ1A1+λ2A2仍为正定矩阵,根据凸集的定义知,B(n)为凸集,但是不包含原点。
引理2:当r=n-1时,集合B(n-1)={A∈Sn×n|A≥0, rank(A)=n-1}不是锥,也不为凸集。
证明:因为B(n-1)不满足锥和凸集的定义,从而可以证明。例如:
| $ {A_1}\left( \begin{array}{l} 1\;\;\;0\\ 0\;\;\;0 \end{array} \right), {A_2} = \left( \begin{array}{l} 0\;\;0\\ 0\;\;2 \end{array} \right) \in B\left( 1 \right) $ |
但有
引理3:集合S(n)={A∈Sn×n|A≥0, rank(A)≤n}为锥,且为凸锥。
证明:根据锥的定义,显然,0矩阵属于S(n),且对∀λ>0,有λA∈S(n),从而S(n)为锥;又∀A1, A2∈S(n),λ1, λ2>0,根据矩阵的正定性可知,λ1A1+λ2A2∈S(n),从而根据凸集的定义知,S(n)为凸集,且包含原点。
同时引理3还表明,因为矩阵A为n阶矩阵,r=n时的秩约束为平凡约束,则此时该集合的约束仅包含正定约束,不包含秩的约束。
引理4:当r≤n-1时,集合S(r)={A∈Sn×n|A≥0, rank(A)≤r}为锥,但为非凸锥。
证明:根据锥的定义可以证明S(r)为锥。根据引理2的反例知道,该锥为非凸锥。
引理5:任意闭凸集为集合的相对内点和集合的边界的并集[16]。另外,还有一个结论——引理6。
引理6:若r1<r2,则S(r1)⊂S(r2)。
证明:由定义显然可证。该引理表明,秩小的锥S(r)在秩大的锥S(r)的边界上。
2 主要结果定理1:半正定矩阵约束S(n)={A∈Sn×n|A≥0, rank(A)≤n}=
证明:根据引理1到引理5可以证明。
由引理1可知,B(n)为不包含原点的凸集,为S(n)的内部;再根据引理5,及引理3中S(n)的性质,从而可以证明:
| $ \begin{array}{l} S\left( n \right) = \overline {\left\{ {A \in {S^{n \times n}}{\rm{|}}A \ge 0, rank\left( A \right) = n} \right\}} \\ \;\;\;\;\;\;\;\; = \overline {B\left( n \right)} = \bigcup\limits_{r = 0}^n {S\left( r \right)} \end{array} $ |
定理2:凸锥S(n)的共轭锥S*(n)也为闭凸锥。
证明:定义矩阵A, B的内积〈A, B〉=tr(ATB),根据共轭锥的定义S*={A*|〈A, A*〉≥0, A∈S(n)},由于S(n)为凸锥,根据凸锥的性质,凸锥的共轭锥仍为凸锥,闭集的共轭仍为闭集,从而S*(n)为闭凸锥。
定理3:半正定矩阵约束
| $ \begin{array}{l} S\left( r \right) = \overline {\left\{ {A \in {S^{n \times n}}{\rm{|}}A \ge 0, rank\left( A \right) = r} \right\}} \\ \;\;\;\;\;\;\;\; = \overline {B\left( r \right)} = \bigcup\limits_{k = 0}^r {S\left( k \right)} \end{array} $ |
证明:该结论的证明可以由集合闭的性质得到。闭集为其内部的闭包,由半正定矩阵秩约束的定义及定理1结论可以证明。
定理4:半正定矩阵秩约束的闭凸锥S(r)的维数为dim(S(r))=r(n-r)+
说明:该结论为文献[17]中的定理3,它证明了半正定矩阵秩约束空间的维数。由该结论可知,半正定矩阵秩约束对应的锥是一个线性空间,且该空间的维数可以计算,从而对该锥空间的性质有了进一步的了解。
3 例子矩阵A∈S2×2,锥S(1)={A∈S2×2|rank(A)≤1}, S(2)={A∈S2×2|rank(A)≤2}(A为半正定矩阵)的图形如图 1所示。
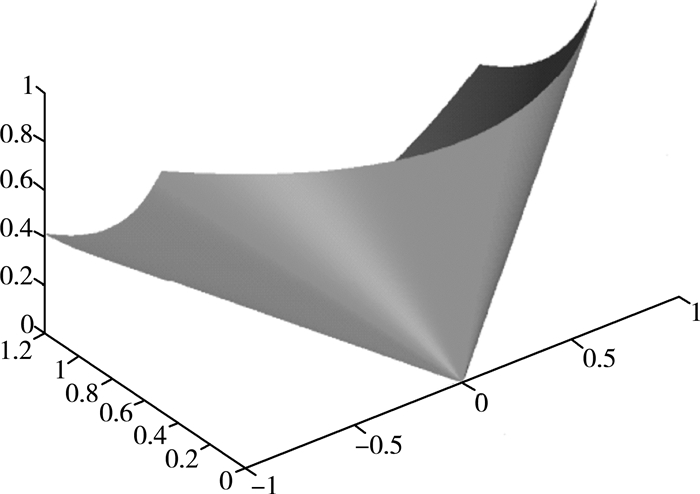 |
| 图 1 例子矩阵图形 |
在图 1中,闭凸锥S(2)为曲面所包含的内部部分且包含边界曲面,为凸锥。其边界曲面为S(1),是锥但不是凸的,因为曲面上元素的线性组合不一定属于该曲面。需要说明的是,当矩阵的维数大于2时,凸锥S(r)的完全图形及其边界无法在三维空间中画出,三维空间只能画出其部分边界的图形。
4 结论讨论了实半正定矩阵锥集合S(r)={A∈Sn×n|A≥0, rank(A)≤r},得到了当r取不同值情况下集合的若干性质,并对该集合的结构与性质进行了初步的研究,得到了几个基本结论。这些结论对于矩阵补全、模型降阶等问题的求解具有一定的理论意义。结论刻画了问题模型中秩约束可行域的几何形状及其性质,对于进一步深刻研究矩阵秩约束优化问题以及问题求解具有一定的价值。最后给出例子验证了结论。
| [1] |
EIGHAOUI L, OUSTRY F, AIT RAmi M. A cone complementarity linearization algorithm for static out feedback problems[J]. IEEE Transaction on Automatic Control, 1997, 42(8): 1171-1176. DOI:10.1109/9.618250 |
| [2] |
FARES B, NOLL D, APKARIAN P. Robust control via sequential semidefinite programming[J]. SIAM Journal of Control Optimization, 2002, 40(6): 1791-1820. DOI:10.1137/S0363012900373483 |
| [3] |
BALAS E, CERIA S, CORNU'EJOLS G. A lift-and-project cutting plane algorithm for mixed 0-1 programs[J]. Mathematical Programming, 1993(58): 295-324. |
| [4] |
Cai J.F., Candes E.J., Shen Z.W.. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20: 1956-1982. DOI:10.1137/080738970 |
| [5] |
GRIGORIADIS K M. Optimal H∞ model reduction via linear matrix inequalities:continuous-and discrete-time cases[J]. Systems & Control Letters, 1995(26): 321-333. |
| [6] |
GERMOL J C, EGAS R G, KAWAOKA F R R. H∞ model reduction with application to flexible systems[J]. IEEE Transactions on Automatic Control, 2005, 50(3): 402-406. |
| [7] |
李久芹, 杨洪礼. 基于秩约束逼近的系统模型降阶[J]. 山东科技大学学报(自然科学版), 2016, 35(6): 114-122. DOI:10.3969/j.issn.1672-3767.2016.06.018 |
| [8] |
JUAN A D, MAEDER M, HANCEWICZ T, et al. Use of local rank-based spatial information for resolution of spectroscopic images[J]. Journal of Chemometrics, 2007, 22(5): 291-298. |
| [9] |
ZHANG X, AD J, TAULER R. Local rank-based spatial information for improvement of remote sensing hyperspectral imaging resolution[J]. Talanta, 2016(146): 1-9. |
| [10] |
MESBAHI M, PAPAVASSILOPOULOS G P. On the rank minimization problem over a positive semi-definite linear matrix inequality[J]. IEEE Transactions on Automatic Control, 1997, 42(2): 239-243. DOI:10.1109/9.554402 |
| [11] |
RECHT B, FAZEL M, PARRILO P A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization[J]. SIAM Review, 2010(52): 471-501. |
| [12] |
MA S, GOLDFARB D, CHEN L. Fixed point and bregman iterative methods for matrix rank minimization[J]. Mathematical Programming, 2011(128): 321-353. |
| [13] |
LU S. Variational conditions under the constant rank constraint qualification[J]. Mathematics of Operations Research, 2010, 35(1): 21-26. |
| [14] |
KRUGER A Y, MINCHENKO L, OUTRATA J V. On relaxing the mangasarian-fromovitz constraint qualification[J]. Positivity, 2014, 18(1): 171-189. DOI:10.1007/s11117-013-0238-4 |
| [15] |
ANDREAN I R, SILVA P J S. Constant rank constraints qualification:a geometric introduction[J]. Pesquisa Operacional, 2014, 34(3): 481-494. DOI:10.1590/0101-7438.2014.034.03.0481 |
| [16] |
刘光中. 凸分析与极值问题. [M]. 北京: 高等教育出版社, 1991: 58-81.
|
| [17] |
ORSI R, HELMKE U, MOORE J B. A Newton-like for solving rank constrained linear matrix inequalities[J]. Automatica, 2006(42): 1875-1882. |
 2018, Vol. 32
2018, Vol. 32


