| H70黄铜局域化剪切变形行为研究 |
绝热剪切是材料在高应变速率变形中局域化塑性变形的一种常见形式, 广泛存在于工业生产中, 例如:高速冲击、高速切削、爆炸复合等[1-3]。绝热剪切带是一条变形高度集中的狭窄带状区域。绝热剪切敏感性指材料发生绝热剪切的难易程度, 绝热剪切敏感性越高越容易发生绝热剪切[4]。绝热剪切带广泛存在于钢[5]、镁合金[6]、铝合金[7]、钛合金[8]、纯铜[9]等材料中, 绝热剪切带内容易产生孔洞和裂纹, 常被视为材料失效的前兆, 因此研究材料的绝热剪切现象具有重要意义。
H70黄铜在生产生活中有广泛的应用, 例如:散热器外壳、垫片、弹壳等, 在加工和使用过程中常处于高应变速率条件下。而关于H70黄铜中绝热剪切现象的研究还很少, 因此本文目的是通过分离式霍普金森压杆技术研究高应变速率下H70黄铜的局域化剪切变形行为, 并分析应变速率对H70黄铜绝热剪切敏感性的影响规律及机理。
1 实验实验研究对象是H70黄铜, 其化学成分如表 1所示。材料初始状态是热挤压态的圆棒, 直径为8 mm, 随后对材料进行退火, 工艺为氩气炉中650 ℃退火20 min, 水冷。
| 表 1 H70黄铜化学成分 |
 |
通过机加工将材料加工成帽形试样, 试样尺寸如图 1所示。帽形试样可以在规定的剪切区域内发生的剧烈的剪切变形, 剪切区域高2.2 mm, 宽0.3 mm。
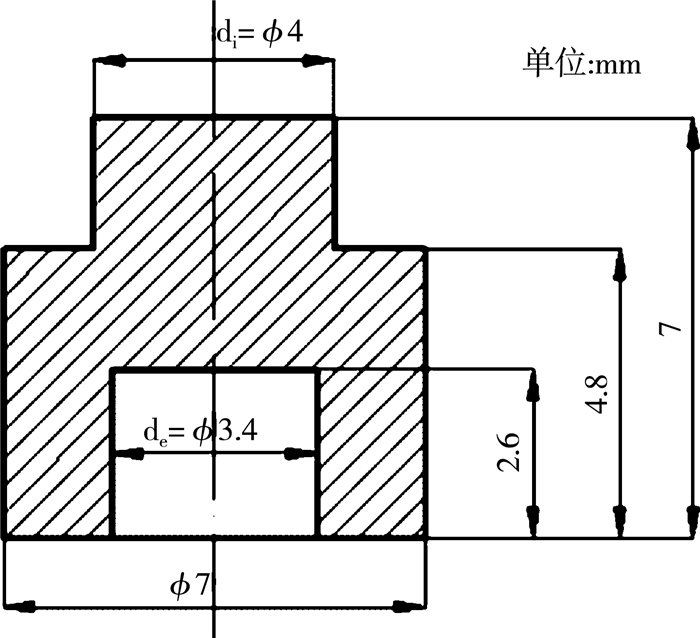 |
| 图 1 帽形试样尺寸 |
利用分离式霍普金森压杆装置对帽形试样进行动态加载, 装置中的入射杆和透射杆长度为1 000 mm、直径为14.5 mm, 子弹的长度为300 mm。实验中选择两种加载气压0.15 MPa、0.20 MPa, 来获得不同的应变速率, 试验温度为293 K。加载后获得相应的电信号曲线, 然后根据公式(1)-(5)可以得到真应力-真应变曲线, 公式如下所示[10]:
| $ \tau = \frac{{{E_0}{A_0}{\varepsilon _t}(t)}}{{\pi h\left( {\frac{{{d_{\rm{i}}} + {d_{\rm{e}}}}}{2}} \right)}} $ | (1) |
| $ \dot \gamma = \frac{{2{C_0}\left[ {{\varepsilon _i}(t) - {\varepsilon _t}(t)} \right]}}{s} $ | (2) |
| $ \gamma = \frac{{2{C_0}\int_0^t {\left[ {{\varepsilon _i}(t) - {\varepsilon _t}(t)} \right]} dt}}{s} $ | (3) |
| $ \sigma = 2\tau $ | (4) |
| $ \varepsilon = \ln \sqrt {1 + \gamma + \frac{{{\gamma ^2}}}{2}} $ | (5) |
式中, τ、
通过金相显微镜观察加载前后试样微观组织形貌。为观察加载后试样微观形貌, 利用线切割将加载后的试样沿轴线分为两半, 对截面进行磨抛、侵蚀, 侵蚀剂为:FeCl3(10 g)+HCl(8 mL)+C2H5OH(50 mL)+H2O(50 mL)。加载前的试样观察面为平行于圆棒轴线的截面。
2 实验结果及讨论 2.1 原始组织形貌特征加载前H70黄铜微观组织形貌如图 2所示, 材料中的晶粒形状为等轴状, 并且存在部分孪晶。利用Nano measurer软件测得材料的平均晶粒尺寸为39.01 μm。且由图 2可得, H70黄铜是典型的单相黄铜, 材料中的晶粒为α相。
 |
| 图 2 H70黄铜原始微观形貌 |
2.2 动态强迫剪切力学响应特征
图 3为试样变形过程的真应力-真应变曲线, 黑色和红色曲线分别对应不同应变速率:
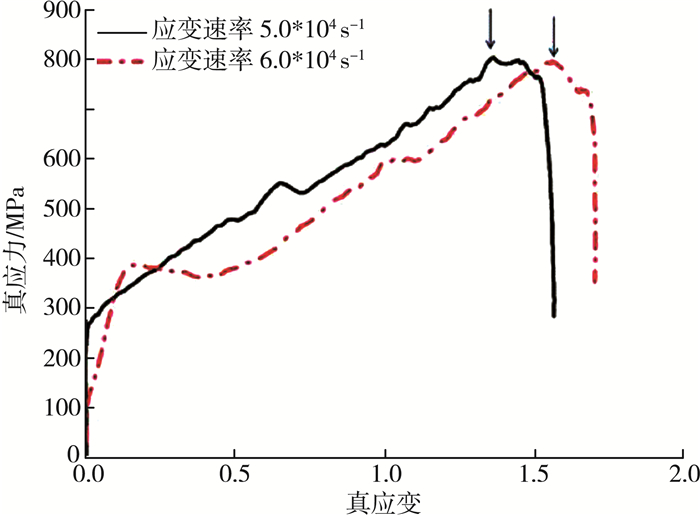 |
| 图 3 不同应变速率下H70黄铜真应力-真应变曲线 |
在一维剪切情况下材料的热-黏塑性本构方程和本构失稳的临界条件可写为[11]:
| $ \tau = f(\gamma , \dot \gamma , T) $ | (6) |
| $ \frac{{d\tau }}{{d\gamma }} = \frac{{\partial \tau }}{{\partial \gamma }} + \frac{{\partial \tau }}{{\partial \dot \gamma }}\frac{{d\dot \gamma }}{{d\gamma }} + \frac{{\partial \tau }}{{\partial T}}\frac{{dT}}{{d\gamma }} = 0 $ | (7) |
式中, τ为剪切应力, γ为剪切应变,
当应变速率为
比较单位体积绝热剪切形成能[12]的大小也可以判断材料绝热剪切敏感性的高低, 绝热剪切发生时所吸收的能量越少, 材料绝热剪切敏感性越高, 单位体积绝热剪切形成能公式如下:
| $ E = \int_0^s \sigma d\varepsilon $ | (8) |
式中, δ为真应力, ε为真应变。根据公式(8), 对图 2中真应力-真应变曲线起始点到应力塌陷点阶段进行积分, 得到当应变速率为
由上可知, H70黄铜的绝热剪切敏感性随着应变速率的增加而降低。绝热剪切现象的发生受到应变硬化作用、应变速率硬化作用和热软化作用的影响, 较高的热软化作用和较低应变硬化作用、应变速率硬化作用均有利于绝热剪切的发生。本试验中, 随着应变速率增加, 变形过程中材料内的位错难以集中, 即应力集中小, 需要更大的外力才能继续变形, 因此导致材料应变硬化作用增加。另外H70黄铜具有低的层错能, 在高应变速率变形中容易发生孪生[13], 孪晶界将对位错运动的阻碍能力更强, 进一步提高了应变硬化作用, 关于孪晶界可以提高材料应变硬化能力的报道已经有很多。Ayman等[14]研究发现, 在变形过程中, 随着变形孪晶的出现, 材料应变硬化速率显著增加。Guo等[15]也发现, 与不含孪晶的AZ31镁合金相比, 含孪晶的试样在变形初期的应变硬化速率更高。因此随着应变速率增加, 应变硬化作用增大, H70黄铜的绝热剪切敏感性降低。
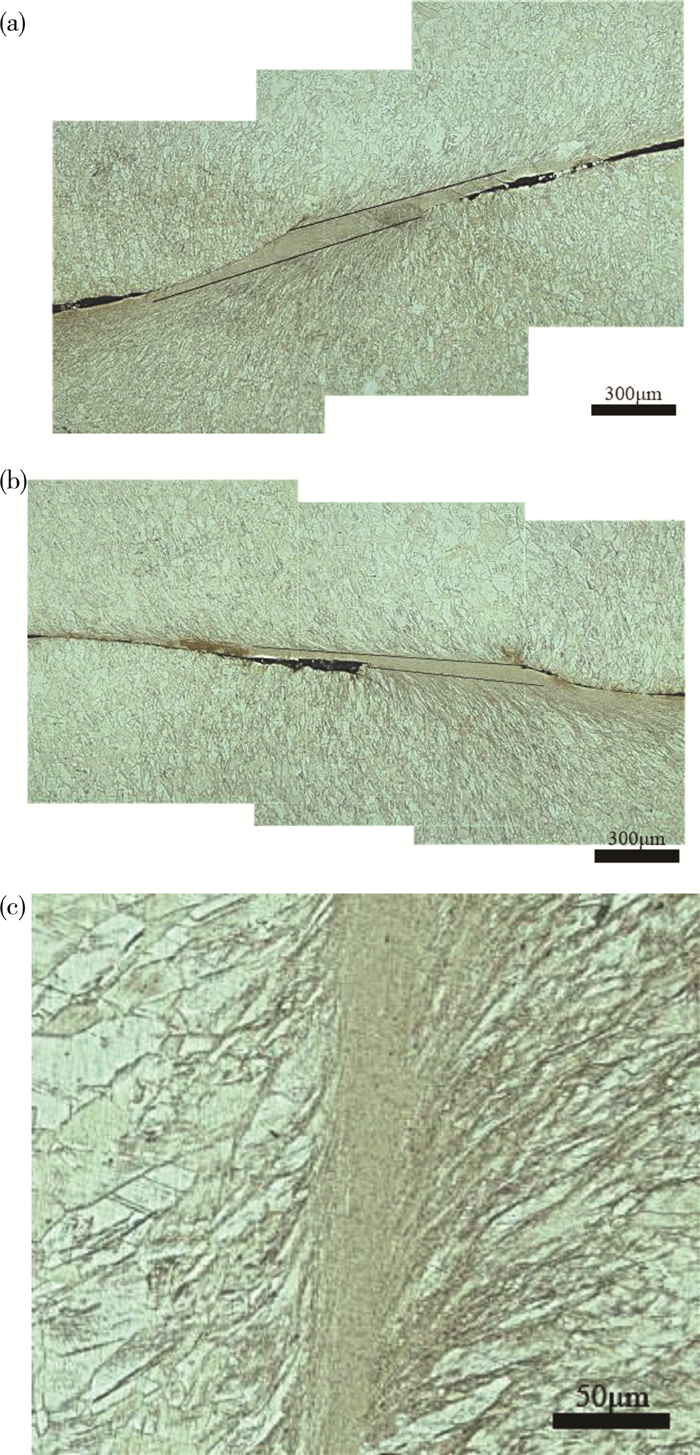
2.3 绝热剪切带形貌观察加载后试样的微观形貌如图 4所示, 加载后试样中出现一条明显的灰色带状区域(其上下边界由图中黑色实线表示), 区域内观察不到明显的晶粒, 表明原始粗大晶粒通过发生再结晶细化为小晶粒, 区域边界处的晶粒发生剧烈塑性变形, 被扭曲拉长, 距离带状区域较远的基体中的晶粒未发生明显变形, 仍呈等轴状, 这个带状区域便是绝热剪切带。
 |
|
(a) |
关于绝热剪切带内晶粒发生再结晶然后细化的现象已经在很多材料中观察到。在变形过程中, 帽形试样剪切区域发生大的塑性变形, 产生的变形功约90%转换为热量, 且由于变形时间短, 热量来不及扩散, 使得试样局部温度升高, 温度的升高为材料内发生再结晶提供了条件。关于绝热剪切带内的再结晶机制已经提出了很多, 目前应用最广泛的是亚晶旋转动态再结晶机制。根据亚晶旋转动态再结晶机制, 在变形过程中, 材料中产生大量的位错, 随着变形的继续, 位错不断增殖、交割, 然后逐渐形成位错胞, 随着进一步变形位错胞渐渐转变为亚晶, 然后亚晶断裂旋转将形成新的细小晶粒[9]。
3 结论通过分离式霍普金森压杆与金相显微镜研究了H70黄铜中的局域化剪切变形行为, 分析了应变速率对H70黄铜绝热剪切敏感性的影响规律:
1) 当应变速率为5.0×104 s-1和6.0×104 s-1时, 加载后H70黄铜均出现了明显的绝热剪切带, 带内观察不到明显的晶粒, 表明发生了动态再结晶。
2) 动态力学响应曲线分析表明, 随着应变速率增加, 对应的临界应变和单位体积绝热剪切带形成能增加, 表明H70黄铜的绝热剪切敏感性随着应变速率增加而降低。
| [1] |
DANNEMANN K A, CHALIVENDRA V B, SONG B. Dynamic behavior of materials[J]. Experimental Mechanics, 2012, 52(2): 117-118. |
| [2] |
LI J Q, XU B C. Study on adiabatic shearing sensitivity of titanium alloy in the process of different cutting speeds[J]. International Journal of Advanced Manufacturing Technology, 2017, 93(6): 1-7. |
| [3] |
YANG Y, WANG BF. Dynamic recrystallization in adiabatic shear band in α-titanium[J]. Materials Letters, 2006, 60(17-18): 2198-2202. DOI:10.1016/j.matlet.2005.12.097 |
| [4] |
YANG Y, JIANG L, LUO S, et al. Effect of grain boundary character distribution on the adiabatic shear susceptibility[J]. Metallurgical and Materials Transactions A, 2016, 47(11): 5589-5597. DOI:10.1007/s11661-016-3721-2 |
| [5] |
BOAKYE-YIADOM S, BASSIM N. Effect of heat treatment on stability of impact-induced adiabatic shear bands in 4340 steel[J]. Materials Science & Engineering A, 2012, 546: 223-232. |
| [6] |
毛萍莉, 刘遵鑫, 刘正, 等. 晶粒大小对AZ31镁合金绝热剪切敏感性的影响[J]. 沈阳工业大学学报, 2015, 37(5): 494-499. |
| [7] |
OWOLABI G M, ODESHI A G, SINGH M N K, et al. Dynamic shear band formation in Aluminum 6061-T6 and Aluminum 6061-T6/Al2O3 composites[J]. Materials Science & Engineering A(Structural Materials:Properties, Microstructure and Processing), 2007, 457(1-2): 114-119. |
| [8] |
SUN K, YU X D, TAN C W, et al. Effect of microstructure on adiabatic shear band bifurcation in Ti-6Al-4V alloys under ballistic impact[J]. Materials Science and Engineering A, 2014, 595: 247-256. DOI:10.1016/j.msea.2013.12.007 |
| [9] |
TANG L, CHEN Z, ZHAN C, et al. Microstructural evolution in adiabatic shear bands of copper at high strain rates:Electron backscatter diffraction characterization[J]. Materials Characterization, 2012, 64: 21-26. DOI:10.1016/j.matchar.2011.11.011 |
| [10] |
ANDRADE U, MEYERS M A, VECCHIO KS, et al. Dynamic recrystallization in high-strain, high-strain-rate plastic deformation of copper[J]. Acta Metallurgica Et Materialia, 1994, 42(9): 3183-3195. DOI:10.1016/0956-7151(94)90417-0 |
| [11] |
王礼立, 余同希, 李永池. 冲击动力学进展[M]. 合肥: 中国科学技术大学出版社, 1992: 3-33.
|
| [12] |
刘新芹, 谭成文, 张静, 等. 应力状态对TI-6AL-4V绝热剪切敏感性的影响[J]. 稀有金属材料与工程, 2008, 37(9): 1522-1525. DOI:10.3321/j.issn:1002-185X.2008.09.004 |
| [13] |
MEYERS M A, VOHRINGER O, LUBARDA V A. The onset of twinning in metals:a constitutive description[J]. Acta Materialia, 2001, 49(19): 4025-4039. DOI:10.1016/S1359-6454(01)00300-7 |
| [14] |
SALEM A A, KALIDINDI S R, DOHERTY R D. Strain hardening of titanium:role of deformation twinning[J]. Acta Materialia, 2003, 51(14): 4225-4237. DOI:10.1016/S1359-6454(03)00239-8 |
| [15] |
GUO L L, CHEN Z C, GAO L. Effects of grain size, texture and twinning on mechanical properties and work-hardening behavior of AZ31 magnesium alloys[J]. Materials Science & Engineering A, 2011, 528(29-30): 8537-8545. |
 2020, Vol. 34
2020, Vol. 34

