| 基于视觉伺服的细胞载玻片精确点胶方法研究 |
点胶机普遍应用于工业生产中的各个行业, 例如:精密机械的条纹印制和密封, 电子元件的粘贴, 以及IC封装的灌胶等[1-2]。但就国内外视觉点胶的应用上来讲, 主要应用领域是电子行业, 对载玻片上的细胞群进行点胶几乎没有出现过。随着科技的发展, 医疗领域的拓广, 细胞观察量的需求正不断上升, 标本制作的工作也随之加大, 因此解决标本点胶的问题迫在眉睫。
实现精确点胶, 其关键技术在于点胶精度的改进, 目前对点胶精度产生影响的主要因素有产品本身的尺寸公差、夹具的设计精度、点胶方式以及点胶的控制方式等。传统的点胶方式主要是通过人工固定输入点胶位置和点胶路径来完成点胶过程的, 它的精度主要通过提高夹具的装夹精度来控制, 不仅点胶精度低, 生产效率亦处于低水平状态[3]。为了实现点胶机自动完成对载玻片进行精确点胶功能, 我们提出了视觉伺服辅助机械臂完成点胶位置的确定方法, 该方法的主要思路是利用摄像头采集载玻片上细胞观察体的位置信息, 通过坐标转换将其位置信息转换为机械臂操作位置信息, 比对其之前设定好的位置得到反馈信息, 若偏差在可控范围内则机械臂按照原来位置进行点胶;若偏差超过设定范围, 则通过视觉伺服系统调整机械臂位置, 使其完成点胶。
1 系统构成本系统主要由四轴桌面机械臂、相机及相机支架、全自动点胶机、晾片板及工作台、计算机构成, 系统构成示意图如图 1所示。
 |
| 图 1 系统构成示意图 |
机械臂与点胶机进行组合, 将料筒与机械臂末端执行器进行固定, 既能实现点胶针头的移动, 又能实时获得点胶针头的位置信息, 固定方式如图 2所示。
 |
| 图 2 固定方式 |
采用眼固定结构的图像采集方式, 将相机固定在机械臂的前上方, 为了避免机械臂作业过程中对相机的碰撞, 又保证不影响图像采集精度, 相机安放的高度要大于机械臂运动最高范围的高度。在已知机械臂的运动空间的前提之下, 为了保证工作区域在CCD相机视野, 我们选取机械臂运动空间之外的位置进行安放支架基座, 安装示意如图 3。
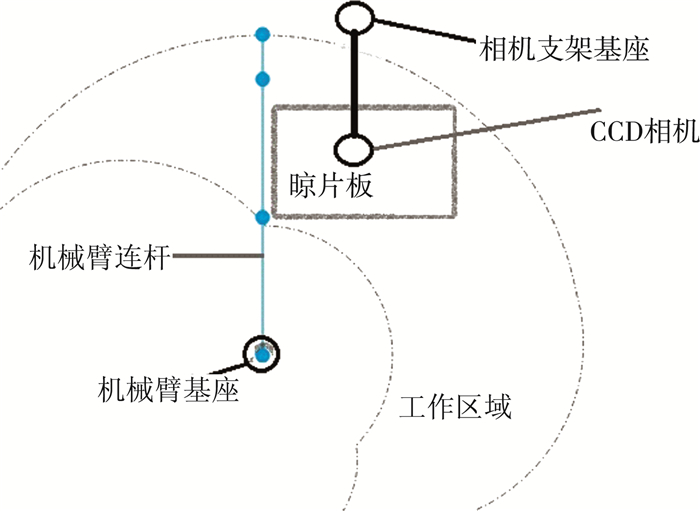 |
| 图 3 相机安装示意图 |
此外, 本文的工作台的设计本着图像预处理采取图像的最佳环境进行设计, 由于图像处理的对象为玻璃材质, 具有一定的反光效果, 光源的选取采用圆顶无影光源(LQ-DMLmm-C)。为了避免其他光线的干扰和突出工作对象与背景的层次感, 工作背景采用黑色基调材料进行设计。
2 系统视觉标定方法由于点胶料筒与机械臂末端执行器进行组合, 所以点胶末端的实时位置可通过机械臂坐标转换实时得到, 我们以机械臂基座坐标系为世界坐标系, 则点胶的实际坐标可以很方便的获取到。所以相机标定采用直接线性法[4], 即在已知点胶的多个点的实际坐标和这些点对应在图像坐标系中的坐标, 通过求解一组线性方程组来获得相机的有关参数。它以针孔成像模型为研究对象, 不考虑如何成像及成像时候的线性补偿, 可以从得到的直接线性变换矩阵求取参数。根据线性变换矩阵与透视矩阵的关系可以知道, 二者之间仅差一个比例因子, 这个比例因子可以用3*4的矩阵去表示, 求解线性方程组的过程就是求解矩阵中各个参数的过程。
假设空间任一点P的三维坐标是(Xw, Yw, Zw), 在相机坐标系下的坐标为(Xc, Yc, Zc), 经过CCD相机摄影后在图像平面上成像, 设像点坐标为(x, y), 对应到图像上的像素坐标为(u, v)。其坐标对应关系可通过下面两个公式求解:
| $ \left[ {\begin{array}{*{20}{c}} {\rm{x}}\\ {\rm{y}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_C}}\\ {{Y_C}}\\ {{Z_C}}\\ 1 \end{array}} \right] $ | (1) |
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\rm{u}}\\ v\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1/k}&0&{{u_0}}\\ 0&{1/I}&{{v_0}}\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} R&T\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_W}}\\ {{Y_W}}\\ {{Z_W}}\\ 1 \end{array}} \right] \end{array} $ | (2) |
令H=A[R T]不考虑成像具体过程, H可以看成一个3*4矩阵, 即
| $ H = \left[ {\begin{array}{*{20}{c}} {{h_{11}}}&{{h_{12}}}&{{h_{13}}}&{{h_{14}}}\\ {{h_{21}}}&{{h_{22}}}&{{h_{23}}}&{{h_{24}}}\\ {{h_{31}}}&{{h_{32}}}&{{h_{33}}}&{{h_{34}}} \end{array}} \right] $ | (3) |
联系上述式子, 可以得到两个关于Hij的线性方程:
| $ \begin{array}{l} {h_{11}}{X_w} + {h_{12}}{Y_w} + {h_{13}}{Z_w} - u{h_{31}}{X_w} - u{h_{32}}{Y_w}\\ = u{h_{34}}\\ {h_{21}}{X_w} + {h_{22}}{Y_w} + {h_{32}}{Z_w} - v{h_{31}}{X_w} - v{h_{32}}{Y_w}\\ = v{h_{34}} \end{array} $ | (4) |
上述线性方程组描述了图像坐标点和三维世界点的关系。要求取H矩阵中的12个未知参数, 需要知道三维世界坐标点和对应的图像坐标点, 每个目标点都可以列写两个方程, 所以至少要取6个目标点才可以求解参数。
相机标定具体实施流程图为:
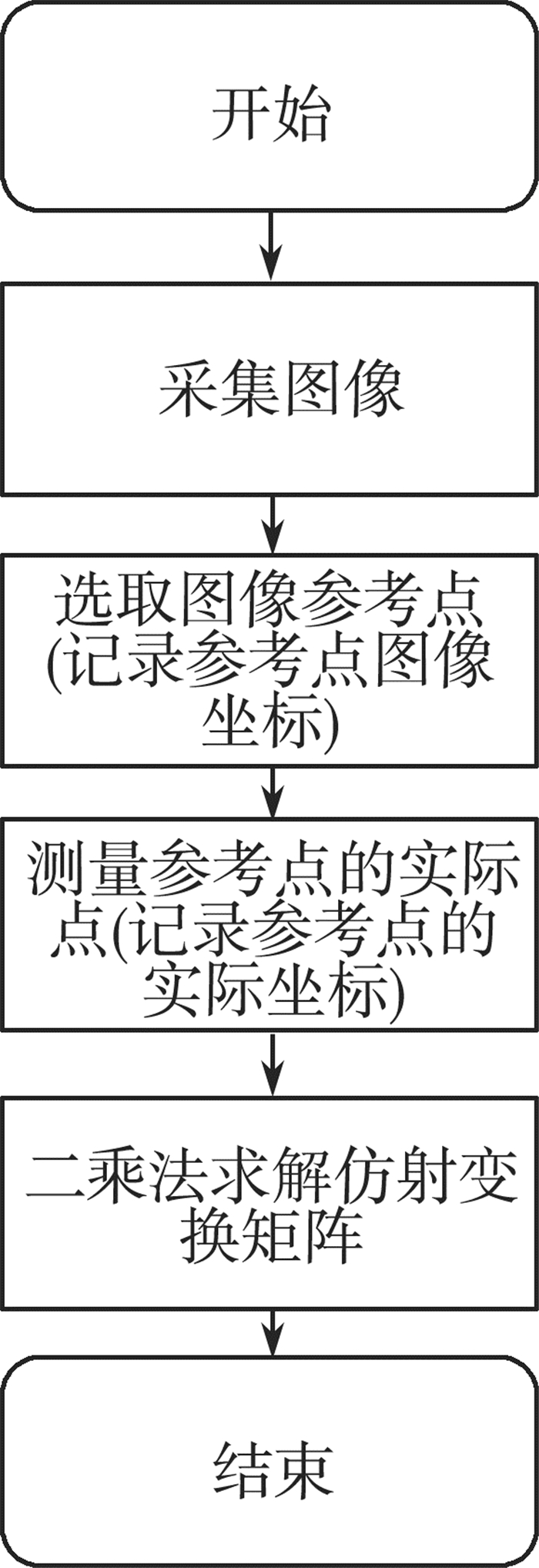 |
| 图 4 标定流程图 |
为了得到更好的标定效果, 本文课题选取10个参考点, 使方程的个数大大超过未知数的个数, 最后采用最小二乘法进行求解。参考点与对应图像参考点坐标如表 1所示。
| 表 1 实验数据 |
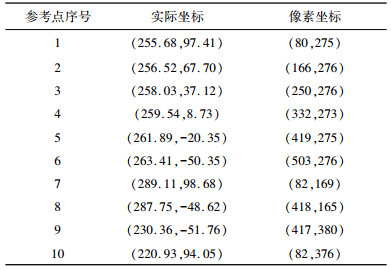 |
利用数学工具MATLAB, 可以求解线性方程组, 最终运算结果在世界坐标系下X轴和Y轴方向上的误差为:
| $ {\rm{err = }}\left[ {\begin{array}{*{20}{c}} {0.054}&{32}\\ {0.093}&{11} \end{array}} \right] $ |
点胶目标粗定位:由于晾片板的位置相对固定, 晾片槽的间距和规格又相对标准, 再加上细胞群在载玻片上的相对位置一致, 所以针对于此工作环境我们可以得到点胶的大概位置。
1) 细胞粘附载玻片位置
本文中以较为常用的载玻片为例, 细胞粘附位置如图 5所示:(根据实际沉降位置得知以右下角边缘为基准的圆心位置)
 |
| 图 5 细胞粘附位置 |
2) 晾片板固定位置
以相机的基座为基准, 采取固定距离放置晾片板, 并进行固定。摆放位置如图 6所示.
 |
| 图 6 晾片板位置 |
3) 点胶位置
以右下角第一片样本的点胶点为起始点开始记录点胶位置, 并以固定间距h向左移动, 重复9次, 分别记录位置信息;然后移动机械臂到达另一排起始点胶位置, 重复上一步操作, 最后根据记录得到的点胶位置数据建立数据库, 以备后用。
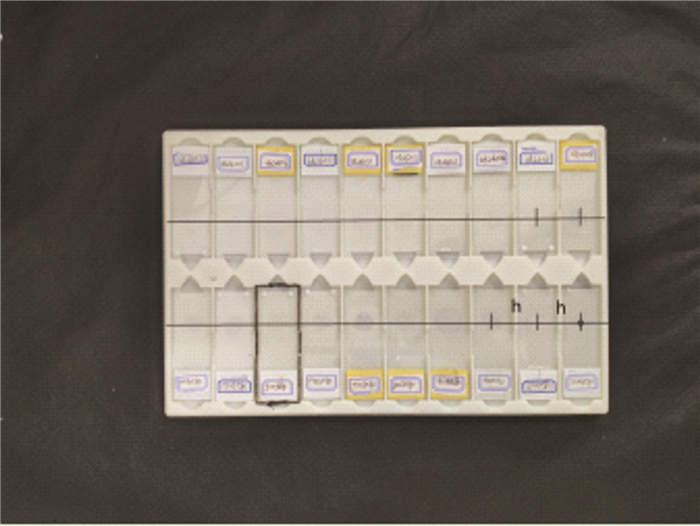 |
| 图 7 点胶位置示例 |
4 点胶目标精确定位
本文中所采集的图像以为五片细胞载玻片样本为例进行图像特征提取来进行说明。
1) 图像采集
图像采集的依据为:能够识别较多的细胞群轮廓为主, 晾片槽的轮廓较为清晰为辅进行图像采集。这样一来既能够在细胞群轮廓较为清晰的前提下成功进行识别, 而且又能避免在细胞群轮廓较为模糊的时候通过识别晾片槽轮廓位置辅助细胞群位置确定。示例采集图像如图 8所示。
 |
| 图 8 采集示例 |
2) 图像预处理
本着消除图像中无关的信息, 恢复有用的真实信息, 增强有关信息的可检测性和最大限度地简化数据, 在目标识别之前先对图像进行预处理。由于本文中要处理的图像的颜色分为两个灰度级, 在进行图像增强便于查找细胞群区域的同时, 也要考虑到同等灰度级之间连通区域的连贯性。因此进行阈值化和直方图均衡化, 另外本文还对图像进行中值滤波处理, 这样在有效抑制脉冲干扰的同时也可一定程度上减轻图像边沿的模糊, 方便识别卡槽轮廓。处理效果如图 9所示。
 |
| 图 9 预处理效果 |
3) 目标识别
通过图像的预处理我们可以发现, 由于样本着色的问题导致有些样本的细胞群在同一阈值下无法显示或无法完整显示, 为了解决这一情况,本文将对两种连通区域进行识别。一是对细胞群轮廓进行识别, 二是对卡槽的三角形区域进行识别。
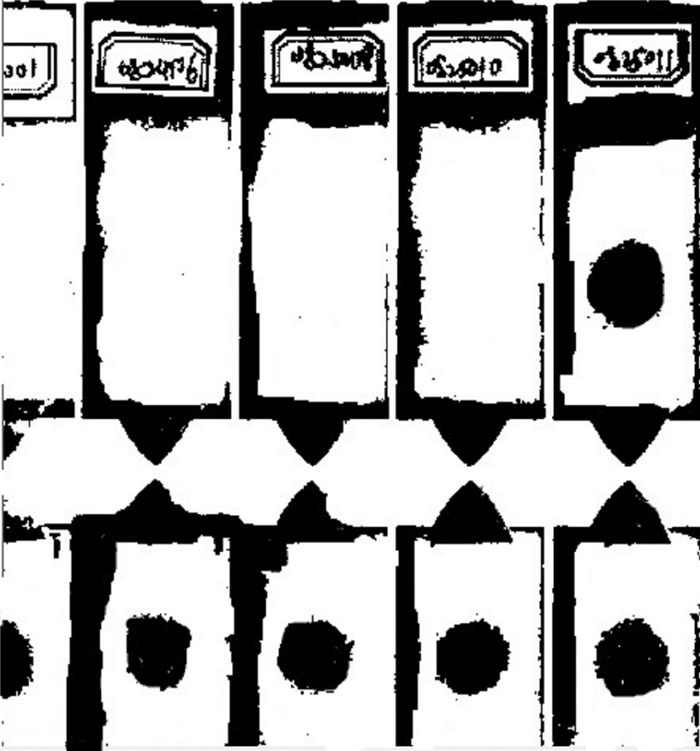
在进行细胞群轮廓区域识别时, 我们观察到要观察的染完色的细胞群的轮廓接近为圆形, 因此我们采用对连通区域的圆形度进行筛选, 经过反复实验以及对样本统计得到圆形度的筛选范围, 最终得到细胞群的连通区域, 进行标记并显示其形心的图像坐标, 如图 10所示。
 |
| 图 10 细胞群轮廓识别 |
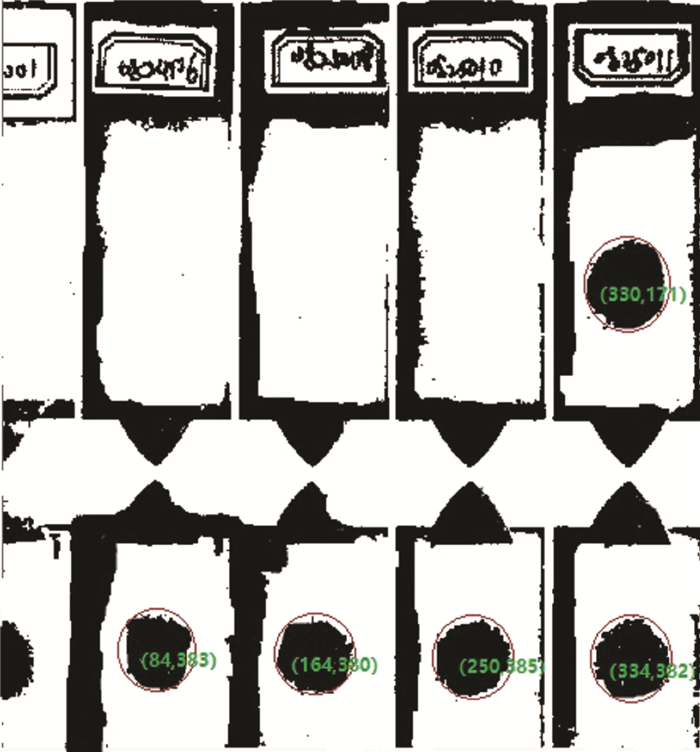
对于没有识别出来的样本, 我们采取的策略是对卡槽的三角形区域进行识别, 从而辅助找到细胞群轮廓的位置。由于图像中三角形的连通区域与卡槽的边缘连通区域未断开, 所以在对三角形连通区域识别之前, 指定分割范围对图像进行分割处理, 分割效果如图 11所示, 然后采用模板匹配进行识别并标记其形心坐标。如图 12所示。
 |
| 图 11 指定分割区域示例 |
 |
| 图 12 三角形区域识别 |
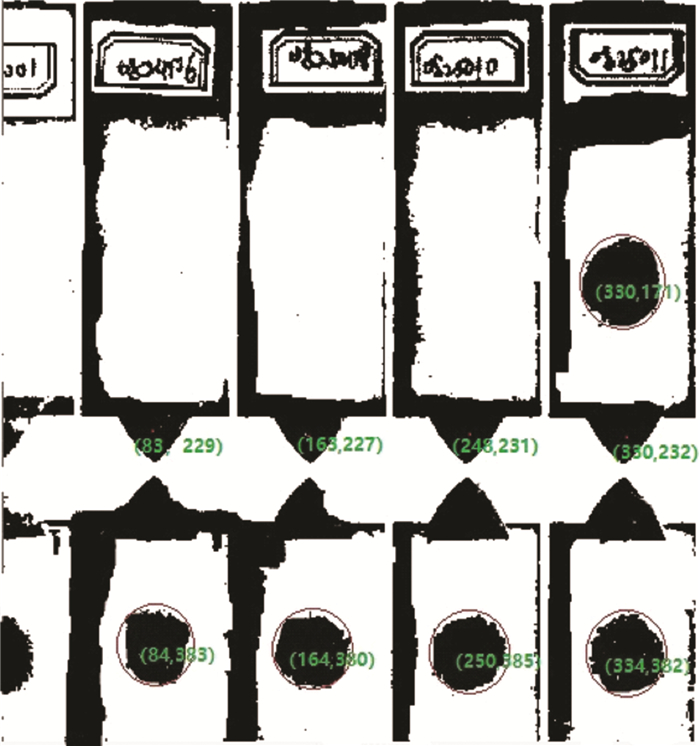
经过反复测量, 我们得到细胞群轮廓的形心到三角形连通区域的形心的图像距离为98, 误差在±2左右。因此在对未识别的样本进行位置确定时, 可通过识别三角形区域的形心坐标在v轴方向上减去98, u轴不变得到对应的细胞群轮廓形心坐标。如图 13所示。
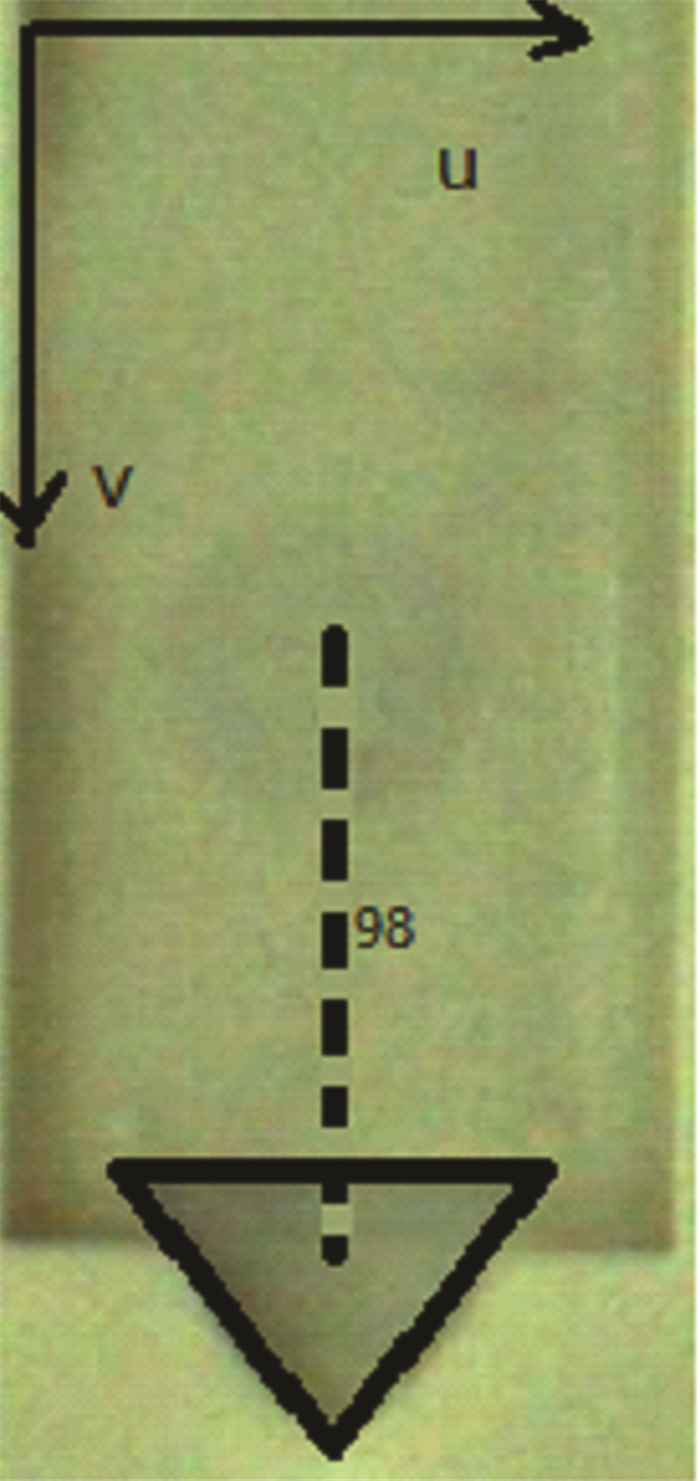 |
| 图 13 定位模拟示例 |
5 伺服系统控制
本设计的伺服系统控制流程如图 14所示。(以第一份样本为例)
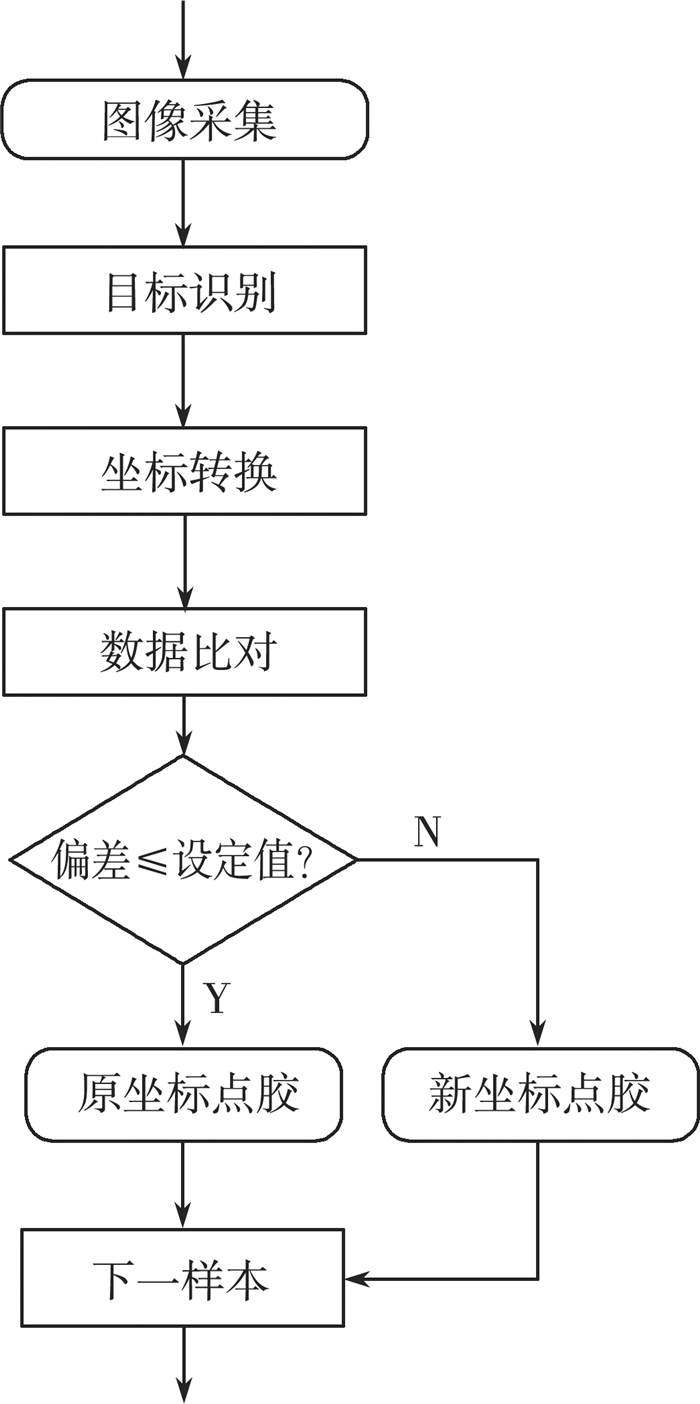 |
| 图 14 系统控制流程图 |
1) 坐标转换
这里的坐标转换是指在获取到像素坐标的基础上转换得到其对应的机械臂坐标。在前边的相机标定的过程中, 我们是以机械臂的基座为世界坐标系进行标定, 其对应参考点的实际坐标是经机械臂控制得到的, 这样一来就建立了图像像素坐标与机械臂控制坐标的关系。因此我们可以通过得到的H矩阵进行求解。
| $ \begin{array}{l} {h_{11}}{X_w} + {h_{12}}{Y_w} + {h_{13}}{Z_w} - u{h_{31}}{X_w} - u{h_{32}}{Y_w}\\ = u{h_{34}}\\ {h_{21}}{X_w} + {h_{22}}{Y_w} + {h_{32}}{Z_w} - v{h_{31}}{X_w} - v{h_{32}}{Y_w}\\ = v{h_{34}} \end{array} $ | (5) |
公式中的ZW基于点胶最佳高度确定。
2) 数据对比
已知第一片样本的原始点胶位置为(X, Y), 通过图像采集得到转换后的坐标为(X*, Y*), 通过公式(5)得到偏差α。
| $ \alpha = {\left( {{X^*} - X} \right)^2} + {\left( {{Y^*} - Y} \right)^2} $ | (6) |
偏差大小所允许范围根据点胶的注入量进行选定, 一旦误差超过此范围则对机械臂传入新的坐标进行操作。
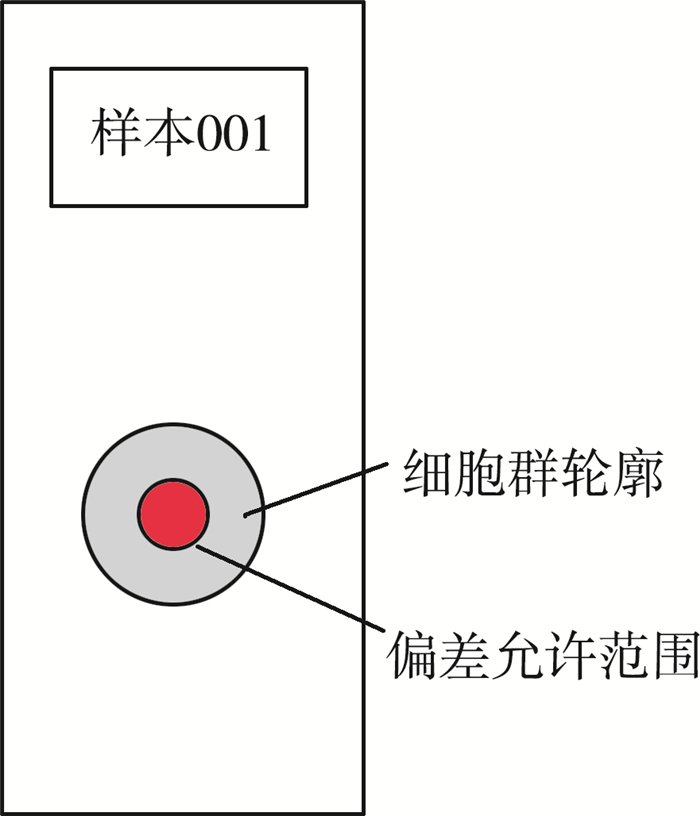 |
| 图 15 偏差允许范围示例 |
注意事项:进行数据对比时, 要对之前操作的位置数据进行采集, 建立数据库方便调用。对于误差范围, 设定警戒范围, 一旦超过警戒范围则对系统进行中断操作防止样本损坏或其他危险事故发生。
以100份样本为一次实验, 细胞群沉淀面积一致, 分五次进行, 通过设定偏差为0.4 mm, 得到加入视觉点胶实验效果与未加入视觉实验效果对比展示表 2。
| 表 2 实验效果对比表 |
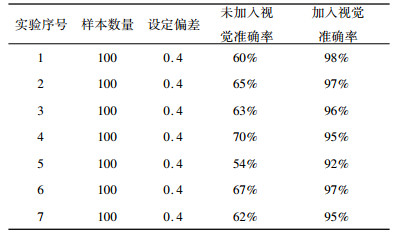 |
通过观察我们发现, 加入视觉的点胶准确率可提高32.71%左右, 满足我们加入视觉的目的, 提高了点胶精度。并且在实际应用中, 我们通过实际操作得到验证, 该方法可以满足病理观察的需求。
6 总结针对细胞载玻片点胶系统的稳定性较差的问题, 研究了基于视觉伺服的细胞载玻片精确点胶系统, 先是对点胶环境进行优化, 得到一组相对稳定的点胶模糊位置;然后利用图像处理技术对细胞群轮廓进行识别定位, 由于考虑到染色不均匀现象, 提出借助对晾片板三角形凹槽识别从而辅助定位, 最后控制四轴桌面机械臂与点胶机协同完成精确点胶, 解决了细胞载玻片点胶系统的稳定性差和点胶准确率较低问题。实验结果表明, 该系统能够提高30%以上的点胶准确率, 满足病理化实验室观察细胞的需求。
| [1] |
段能全, 刘刚, 王俊元. 基于机器视觉的刀具几何参数测量技术田[J]. 机械设计与制造, 2008(10): 217-219. DOI:10.3969/j.issn.1001-3997.2008.10.090 |
| [2] |
YUNG TING, CHIH-HO CHCN, FCNG HUI-YI, et al. Glue dispenser route inspection by using computer vision and neural network[J]. Int J AdvManuf Tcchnol, 2008(39): 9-10. |
| [3] |
谢俊. 基于机器视觉的点胶系统的设计与研究[J]. 电子测量技术, 2016, 39(05): 80-83, 88. DOI:10.3969/j.issn.1002-7300.2016.05.023 |
| [4] |
杜荣.基于机器视觉的工业机器人分拣技术研究[D].南京: 南京林业大学, 2009.6.
|
 2020, Vol. 34
2020, Vol. 34


