| 基于改进适应度函数的麻雀搜索算法路径规划研究 |
随着现代工业与计算机技术的发展, 机器人逐渐应用在各个领域[1], 例如在民用领域的机器人运送快递、自动耕种机, 工业领域的机械臂、水下无人勘探机, 军用领域的无人机侦察、无人轰炸机等[2]。而每个移动机器人在实施目标前都有一个基础——路径规划, 移动机器人只有按照预期抵达目标地点方可进行下一步工作, 所以移动机器人路径规划是智能移动机器人发展技术的关键[3]。
移动机器人的路径规划通常需要在整体环境中规划一条最短路径或最优路径[4]。早期常用的路径规划算法有A-star算法[5]、Dijkstra算法[6]、快速扩展随机树等[7]。此类传统路径规划算法结构简单、约束较少、稳定性强, 适合早期的机器人进行简单场景的路径规划。但随着计算机的技术的飞速发展, 计算机的运算能力逐步增强, 对于智能仿生算法的运算能力也在逐步增强。此外, 相对于传统路径算法灵活性差、改进空间小、应用领域受限制的缺点, 智能仿生算法具有约束多、灵活性高、寻优能力强、模块化设计方便、不同智能仿生算法之间去劣存优的优点, 因此近年来许多智能仿生算法被应用于路径规划领域[8]。在智能仿生算法中, 麻雀搜索算法有以下优点: (1)麻雀搜索算法于2020年被设计出, 改进空间较大。(2)麻雀搜索算法由3类种群相互配合进行寻优, 寻优能力较强。(3)麻雀搜索算法中本代种群受上代种群影响较深, 前期收敛速度较高。因此本文利用麻雀搜索算法应用于地面二维移动机器人路径规划, 并针对麻雀搜索算法在路径规划过程中出现的陷入局部最优、寻路失败的问题[9], 对麻雀搜索算法的适应度函数进行改进使其加快收敛速度, 避免局部最优个体的误导导致的非最优路径或寻路失败情况, 增加寻路成功率。
1 地图环境模型本文的算法实现在栅格地图环境中[10], 栅格地图将环境信息划分为若干正方形栅格, 栅格信息由不同颜色表示[11]。本文有关地图环境的信息用黑白方块表示。如图 1所示, 黑色方块是表示不可通过区域的障碍物, 白色方块是表示可通过的区域的自由空间。
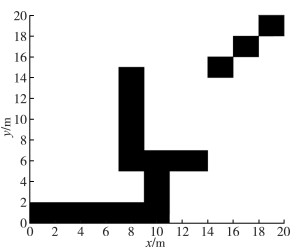 |
| 图 1 地图环境模型 |
栅格地图将地图信息存储在矩阵M(a, b)中, 其中a和b代表栅格地图中的位置信息。在矩阵中, 0代表自由路径区域, 1代表障碍物, 即不可通过的区域。
2 麻雀搜索算法 2.1 麻雀搜索算法基本原理麻雀搜索算法(Sparrow search algorithm, SSA)由薛建凯等[12]于2020年提出, 其灵感源于对自然界中麻雀群体通过团队协作获取食物与躲避捕食者的行为。在麻雀搜索算法中, 适应度越优的麻雀越容易获得食物, 此类麻雀被称为发现者, 将带领团体进行觅食。发现者的位置更新方式为:
| $ x_{i, j}^{t+1}=\left\{\begin{array}{ll} x_{i, j}^{t} \cdot \exp \left(\frac{-i}{\alpha \times T_{\max }}\right), & R<\mathrm{ST} \\ x_{i, j}^{t}+Q \cdot \boldsymbol{L}, & R \geqslant \mathrm{ST} \end{array} 。\right. $ | (1) |
在式(1)中, i代表某个麻雀, j是维数, t表示当前迭代的次数, j∈[1, d], d为整体维度。xi, jt为麻雀第t代的位置, α∈(0, 1), Tmax为最大迭代次数, R表示当前警戒值, ST表示安全阈值, Q是一个服从正态分布的随机数, L是一个每个元素都为1的1×d维矩阵。当R < ST时警戒值低于安全阈值, 此时整个种群将进行大范围搜索; 当R≥ST时表示危险度过高, 种群将趋向于远离危险区域。
麻雀团体中, 部分麻雀会由发现者带领进行觅食行为, 此类麻雀为加入者。加入者会加入发现者进行觅食行为, 同时加入者也可能成为发现者, 其位置更新公式为:
| $ x_{i, j}^{t+1}=\left\{\begin{array}{ll} Q \cdot \exp \left(\frac{x_{w}^{t}-x_{i, j}^{t}}{i^{2}}\right), & i>\frac{n}{2} \\ x_{P}^{t+1}+\left|x_{i, j}^{t}-x_{P}^{t+1}\right| \cdot \boldsymbol{A}^{+} \cdot \boldsymbol{L}, & i \leqslant \frac{n}{2} \end{array}\right. 。$ | (2) |
在式(2)中, xwt表示在第t代中适应度最差的麻雀的位置, xPt+1表示第t+1代时全局最优个体的位置, A为一个1×d维矩阵, 矩阵中的元素都随机预设为-1或1, 并且A+AT(AA)T-1。当
麻雀在觅食过程中, 部分麻雀需要保证整个团体的安全问题, 引导团体躲避捕食者, 此类麻雀被称为侦察者, 其位置更新公式为:
| $ x_{i, j}^{t+1}=\left\{\begin{array}{ll} x_{b}^{t}+\beta \cdot\left|x_{i, j}^{t}-x_{b}^{t}\right|, & f_{i} \neq f_{g} \\ x_{b}^{t}+k \cdot\left(\frac{x_{i, j}^{t}-x_{b}^{t}}{\left|f_{i}-f_{w}\right|+\varepsilon}\right), & f_{i}=f_{g} \end{array}\right. 。$ | (3) |
在式(3)中, xbt表示迭代次数为t时的全局最优位置, β负责控制步长, 其服从均值为0、方差为1的正态分布, k∈[-1, 1], ε为不为0的常数, 避免分母为0。fi为当前个体的适应度值, fg为全局最优个体适应度值, fw为全局最差个体适应度值。当fi≠fg时表示该麻雀需要改变位置来使适应度趋于最优适应度; 当fi=fg时表示此麻雀将向着较优麻雀群体靠拢。
2.2 适应度函数适应度函数是仿生智能算法迭代过程评价的关键, 算法根据当代的适应度值来进行下一代种群个体的选择, 适应度的灵感来源于自然界“优胜劣汰”的生物生存原则[13]。在SSA中, 适应度函数用以淘汰种群中适应度不好的个体, 选择适应度好的发现者或加入者成为发现者作为局部最优进入下一代。在SSA应用于路径规划过程中, 路径的长短、路径是否经过障碍物、个体是否越过边界为适应度函数评价种群的标准, SSA路径规划适应度函数模型为:
| $ F_{i}=\left\{\begin{array}{ll} \sum\limits_{i=1}^{d-1} \sqrt{\left(x_{i+1}-x_{i}\right)^{2}+\left(y_{i+1}-y_{i}\right)^{2}}, & G=0 \\ d_{x} \cdot d_{y} \cdot G, & G \neq 0 \end{array}\right. 。$ | (4) |
在式(4)中, Fi表示当前种群个体的适应度值, xi表示该个体的i节点在地图中的x轴位置, xi+1表示此个体的i+1节点的x轴位置, yi表示该个体的i节点在地图中的y轴位置, yi+1表示此个体的i+1节点的y轴位置。dx、dy为地图环境的长与宽。G表示本代中个体节点刷新在障碍物位置的数量。当G≠0时, 表示此个体所含节点位置刷新在障碍物上, 此类节点存在越多Fi越高。当G=0时, 表示所有个体节点都刷新在自由空间, 此时个体中节点的距离越远Fi越高, 距离越近Fi越低。当节点的位置x或y大于维度dx或dy时Fi取无限大。因此在麻雀搜索算法路径规划中, Fi值越高表示麻雀个体i适应度越不好, 应当淘汰或尽快向最优靠拢, Fi值越低表示麻雀个体i适应度越好, 应当加入下一代。
3 改进适应度函数在SSA路径规划中, 将个体与路径是否接触障碍物, 路径长短作为判断个体优劣的标准。当某个个体不接触障碍物且路径长度较短时将成为本代的最优个体, 但迭代初期全局可能存在许多此类个体, 此时若没有其他判断标准时极易陷入局部最优, 导致收敛速度降低或路径非最优。因此本文将算法迭代过程中当前代的临时全局路径加入到适应度函数中作为个体的判断标准, 对较优的麻雀种群个体进行二次淘汰, 平衡局部最优与全局最优的选择, 通过“优中选优”原则避免局部最优个体的误导导致的非最优路径或寻路失败情况, 提高寻路效率。
改进方法的原理为: 假设个体xn符合局部最优个体适应度值, 则在式(4)之前先对该局部最优个体进行全局路径判断, 即连接起点、终点与所有节点位置, 从起点开始依次选取相邻的3个节点位置n、n+1、n+2, 若3个节点两两之间路径存在障碍物, 则继续选取下一组节点位置, 即n+1、n+2、n+3;若3个节点两两之间路径不存在障碍物或选取位置的过程中无法选取除终点外的下一个节点, 如图 2中点n所示, 则直接淘汰3个节点中的中间节点n+1, 并由适应度函数重新评价本代个体适应度值, 挑选最优个体进入下一代迭代。
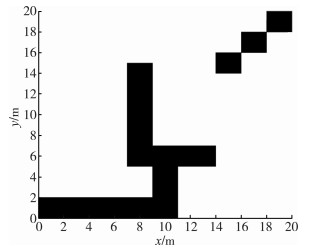 |
| 图 2 局部最优个体 |
改进后的适应度函数判断流程如图 3所示:
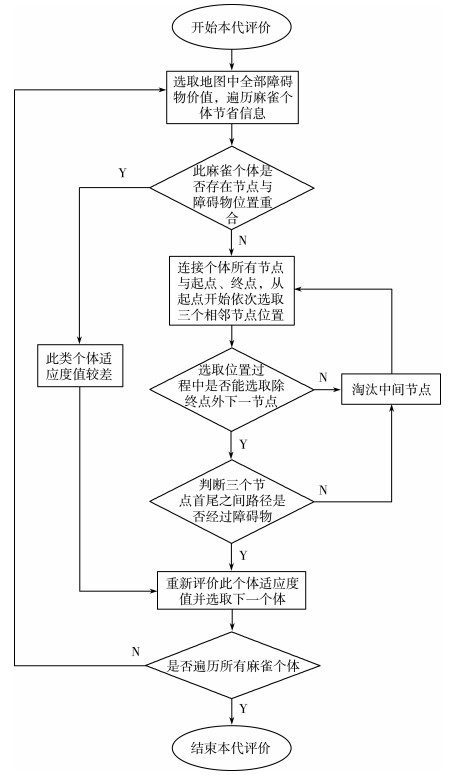 |
| 图 3 改进适应度函数流程图 |
4 实验结果分析
本文SSA预警值的安全阈值设置为0.8, 发现者比重设置为50%, 侦察者比重设置为20%, 种群数量设置为50, 最大迭代次数设置为500, 起点设置为(1, 1), 终点设置为(20, 20)。实验基于MATLAB R2021b实现。为确认实验合理性, 分别设置3种地图环境作为3组实验并与灰狼优化算法(Grey Wolf Optimizer, GWO)[14]路径规划进行对比, 第一组实验、第二组实验、第三组实验的路径与适应度值对比分别如图 4、图 5、图 6所示。
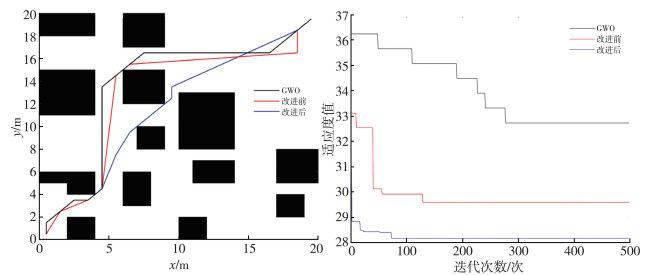 |
| 图 4 第一组实验路径与适应度值对比 |
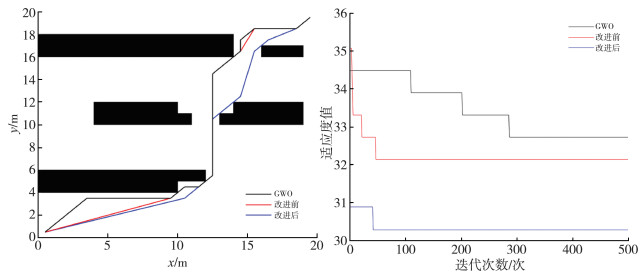 |
| 图 5 第二组实验路径与适应度值对比 |
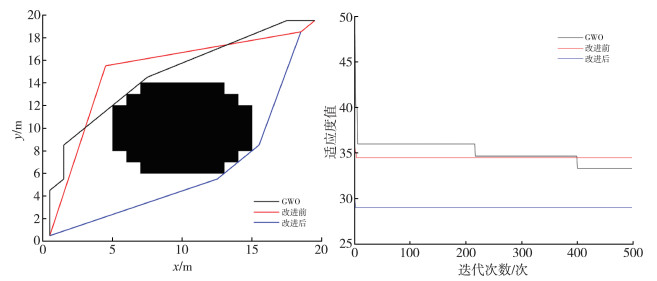 |
| 图 6 第三组实验路径与适应度值对比 |
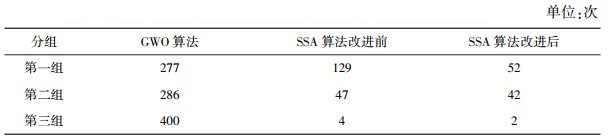
对于3组实验, 到达最佳适应度值所用迭代次数如表 1所示, 路径长度对比如表 2所示。
| 表 1 GWO与SSA算法改进前后达到最佳适应度所用迭代次数 |
 |
| 表 2 GWO与SSA算法改进前后路径长度 |
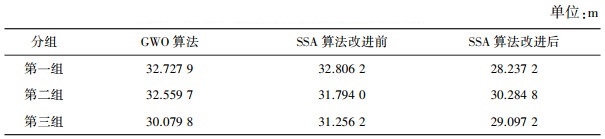 |
实验结果表明, 麻雀搜索算法在路径规划领域寻优能力与灰狼优化器相差不大, 但收敛速度高于灰狼优化器。适应度函数改进后与改进前相比, 收敛速度有所提升, 且场景较复杂的情况下改进提升效果较好, 最佳适应度值降低表明改进后寻优能力更强, 此外改进后的路径长度缩短, 成功避免了个别局部最优个体的误导, 综合提高了麻雀搜索算法路径规划的寻路效率。
5 总结本文将麻雀搜索算法应用于路径规划领域, 并针对特用于路径规划的适应度函数原本的不足, 利用判断误导性局部最优个体的方法在本代中进行二次选择, 提高进入下一代的个体有效性, 为算法整体的稳定性设立良好的前提, 从而提高了算法收敛速度与寻路的成功率和稳定性。最后通过仿真实验验证了改进方法的有效性。
| [1] |
CUI Y, DAI X, DAI L C, et al. An Overview on the Development and Application of Cognitive Robot[C]. proceedings of the 8th International Conference on Fuzzy Systems and Data Mining, FSDM 2022, November 4, China, F, IOS Press BV. 4.
|
| [2] |
WAHAB M N A, NEFTI-MEZIANI S, ATYABI A. A comparative review on mobile robot path planning: Classical or meta-heuristic methods?[J]. Annual Reviews in Control, 2020, 50: 233-252. DOI:10.1016/j.arcontrol.2020.10.001 |
| [3] |
王鹤静, 王丽娜. 机器人路径规划算法综述[J]. 桂林理工大学学报, 2022, 1-15. |
| [4] |
SHAHID N, ABRAR M, AJMAL U, et al. Path planning in unmanned aerial vehicles: An optimistic overview[J]. International Journal of Communication Systems, 2022, 35(6): e5090. DOI:10.1002/dac.5090 |
| [5] |
HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. DOI:10.1109/TSSC.1968.300136 |
| [6] |
张飞凯, 黄永忠, 李连茂, 等. 基于Dijkstra算法的货运索道路径规划方法[J]. 山东大学学报(工学版), 2022, 52(6): 176-182. |
| [7] |
王梓强, 胡晓光, 李晓筱, 等. 移动机器人全局路径规划算法综述[J]. 计算机科学, 2021, 48(10): 19-29. |
| [8] |
音凌一, 向凤红. 融合改进灰狼优化算法和人工势场法的路径规划[J]. 电子测量技术, 2022, 45(3): 43-53. |
| [9] |
王玲玲, 孙磊, 丁光平, 等. 基于改进麻雀搜索算法的无人机航路规划研究[J]. 弹箭与制导学报, 2022, 42(6): 55-60. |
| [10] |
BAI X G, LI B H, XU X F, et al. USV path planning algorithm based on plant growth[J]. Ocean Engineering, 2023, 273: 113965. |
| [11] |
郝琨, 邓晁硕, 赵璐, 等. 基于区域搜索粒子群算法的机器人路径规划[J]. 电子测量与仪器学报, 2022, 36(12): 126-135. |
| [12] |
XUE J K, SHEN B. A novel swarm intelligence optimization approach: Sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
| [13] |
玄登影, 王福林, 高敏慧, 等. 一种改进适应度函数的遗传算法[J]. 数学的实践与认识, 2015, 45(16): 232-238. |
| [14] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. |
 2023, Vol. 37
2023, Vol. 37


