| 无刷直流电机定子采样电流无硬件零漂在线补偿 |
在无刷直流电机控制过程中, 定子电流采样是进行各种控制算法的基础。定子电流采样精确度直接影响电机控制的准确度。在定子电流采样过程中, 由于运放的存在会使定子电流采样零点值发生偏移。为了提高电机控制性能, 需要对电机运行中运放产生零点漂移进行相应补偿。为此, 国内外学者已经开展了大量的研究, 并提出了多种零漂补偿的方法。
文献[1]在分析传统的运算放大器存在着零点漂移、非线性误差等一系列问题的基础上, 提出一种基于斩波稳零运算放大器补偿零漂的方法。文献[2]针对传感器的零点漂移问题, 采用硬件电路实现背向传输神经网络算法, 完成传感器零点漂移的补偿。文献[3-4]描述了一种针对直流母线电压、定子采样电流监测, 通过监测值在线修正的方法补偿直流母线电压和定子采样电流。文献[5-6]为改进抑制零点漂移的技术, 提出了利用一种新型的器件来抑制零点漂移的方法。文献[7]提出了一种基于最小二乘曲线拟合方法的信号调理电路误差补偿方法, 应用该方法可以得到信号调理电路的误差曲线, 通过误差曲线进行分析得到误差进行补偿。文献[8]针对放大器的零漂问题而产生的测量精度低的问题, 提出了一种简单的谐振式观测器对低定子频率下存在的电流测量误差进行补偿。文献[9]提出一种在采样电路前安装电流调零电路, 搭建了对运放零漂进行自动补偿的硬件电路模型。
综上所述, 现有的电流采样零漂补偿的方法都采用硬件电路进行采样的补偿, 但是硬件的方法存在系统跟随性差、补偿不准确、硬件电路设计复杂、增加系统硬件成本等问题。为了弥补上述方法的缺点和不足, 本文采用无硬件定子电流在线补偿的方法对无刷直流电机定子电流采样进行零漂补偿。通过系统初始化获得定子电流零点漂移初值。首先对相电流进行离线补偿, 但是在电机运行过程中时间和环境发生变化, 运放产生的零漂值也会发生变化, 电机运行中零漂值不易检测。针对该问题, 对定子相电流进行积分运算, 计算得到离线补偿后的零漂值, 使其对相电流修正。最后, 搭建系统实验平台, 研究验证了定子电流无硬件零漂补偿的有效性。
1 运算放大器零漂分析 1.1 运放零漂的引入在电机运行过程中通过AD采样获得定子相I_S1。I_S1电流需要经过运放进行电流信号的放大得到I_M1, 电流放大电路如下图 1所示。引入运放器件就会增加零点漂移测量中的误差。
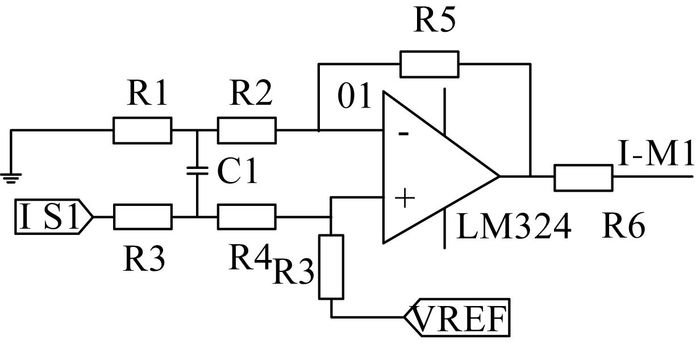 |
| 图 1 定子采样电流放大器结构图 |
零点漂移是指当放大电路输入定子电流采样信号为零时, 由于环境温度的变化、电源电压不稳等因素的影响, 使静态工作点发生变化, 并被逐级放大和传输, 导致电路输出端电压偏离原固定值而上下漂动的现象。显然, 放大电路级数愈多、放大倍数愈大, 输出端的漂移现象愈严重。严重时, 有可能使输入的微弱信号湮没在漂移之中, 无法分辩, 从而达不到预期的传输效果。在电机运行过程中,由于引入运算放大器对定子电流采样值进行处理, 环境温度发生变化就会导致运放的零点漂移值发生变化, 影响定子采样电流的准确性, 使得定子电流采样值存在偏移误差, 最终影响电机控制。
1.2 零漂对转矩影响分析为实现电机电流环的矢量控制, 通常将三相静止坐标系下的相电流通过坐标变换转换到两相旋转坐标系下。变换后在旋转两相坐标系下的电流检测值可以表示为:
| $\left\{ \begin{array}{l} i_d^m = {i_d} + \mathit{\Delta }I\sin \left( {{\theta _e} + \alpha } \right)\\ i_q^m = {i_q} + \mathit{\Delta }I\cos \left( {{\theta _e} + \alpha } \right) \end{array} \right.$ | (1) |
式中iq、id、iqm、idm分别为两相旋转坐标系下的实际电流值和测量值, 公式(1)中ΔI、α、θe由公式(2)计算得到。
| $\left\{ \begin{array}{l} \mathit{\Delta }I = \sqrt {{{\left( {\mathit{\Delta }i_a^{offest}} \right)}^2} + {{\left( {\mathit{\Delta }i_a^{offest} + 2\mathit{\Delta }i_b^{offest}} \right)}^2}/3} \\ \alpha = \arctan \left( {\sqrt 3 \mathit{\Delta }i_a^{offest}/\left( {\mathit{\Delta }i_a^{offest} + 2\mathit{\Delta }i_b^{offest}} \right)} \right)\\ {\theta _e} = 2{\rm{ \mathsf{ π} }}{f_e}t \end{array} \right.$ | (2) |
式中fe为相电流基频。
若系统运行过程中电机转矩模型不变, 则电机输出的实际转矩可以表示为:
| $\begin{array}{l} {T_e} = \frac{3}{2}p{\psi _f}{i_q} = \frac{3}{2}p\psi _f^*\left( {i_q^m - \mathit{\Delta }I\cos \left( {{\theta _e} + \alpha } \right)} \right)\\ \quad = T_e^* - \mathit{\Delta }{T_{offest}} \end{array}$ | (3) |
式中ΔToffset=kt*ΔIcos(θe+α),为由偏移误差导致的脉动转矩;kt*=1.5pnψf*,为转矩系数。
由上述分析得, 偏移误差会导致电机输出的实际转矩在指令转矩附近以电流基波频率波动, 波动幅值与相电流的偏移量有关。
2 电流采样在线零漂补偿算法传统零漂离线补偿的原理为:在电机运行前系统参数初始化时, 电机静止,无定子相电流;对定子电流进行采样, 获得初始状态零点偏移值, 并将其存入寄存器中;电机运行中采样得到的定子电流需要减去零点偏移值。
虽然可以通过离线采样得到一个较准确的零漂初值, 但是在电机长期运行中随着环境和时间的变化, 零漂值也会发生变化。由于在系统运行的过程中无法停机进行零点偏移值的采样, 因此提出了一种无硬件在线零漂补偿的方法, 来校准定子电流值, 使得定子电流采样更加准确。
对获取的定子电流进行在线积分, 得到如下公式:
| $\left\{ \begin{array}{l} i_{a\_m}^{offest} = \int_0^{2{\rm{ \mathit{ π} }}} {i_a^md{\theta _e}} \\ \quad \quad = \int_0^{2{\rm{ \mathit{ π} }}} {\left( { - {k_a}I\sin {\theta _e} + \mathit{\Delta i}_a^{offest}} \right)} d{\theta _e}\\ \quad \quad = 2{\rm{ \mathit{ π} }}i_a^{offest}\\ i_{b\_m}^{offest} = \int_0^{2{\rm{ \mathit{ π} }}} {i_b^md{\theta _e}} \\ \quad \quad = \int_0^{2{\rm{ \mathit{ π} }}} {\left( { - {k_b}I\sin \left( {{\theta _e} - \frac{{2{\rm{ \mathit{ π} }}}}{3}} \right)\mathit{ + \Delta i}_b^{offest}} \right)} d{\theta _e}\\ \quad \quad = 2{\rm{ \mathit{ π} }}i_b^{offest} \end{array} \right.$ | (4) |
从公式(4)中可以看出, 相电流的积分ia_moffest仅与零漂误差Δiaoffest大小相关。减小误差的方法就是对采样得到的定子电流进行积分, 以积分值作为误差进行定子电流的在线补偿值。
基于无硬件零漂在线补偿结构图如图 2所示。
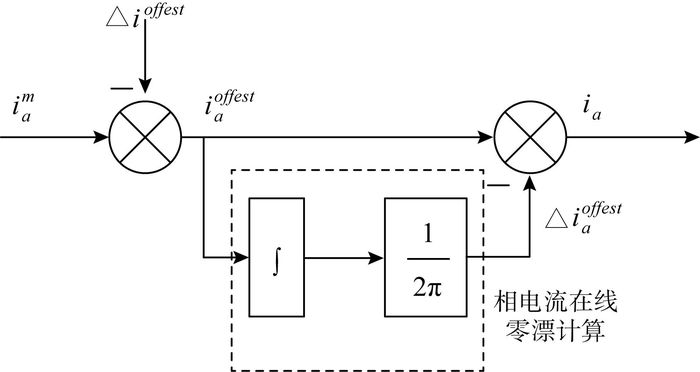 |
| 图 2 电流零点补偿结构图 |
系统在电机运行前对偏移值进行采样, 并将其放入处理器寄存器中。对每次采样得到的值进行离线补偿, 在此基础上对所获得的定子采样电流在0~2π进行积分。由公式(4)得到Δiaoffest=Iboffset/2π, 再由定子采样电流减去Δiaoffest;当采集的电流积分
为了验证所提出的零漂补偿算法的有效性, 在小功率直流无刷电机实验平台上进行了实验验证。本实验所用的直流无刷电机的具体参数见表 1。
| 表 1 无刷直流电机参数 |
 |
本实验所用的直流无刷电机控制器以STM32F103芯片为核心, 采用无传感器矢量控制策略, 外围电路包括驱动电路、采样电路、ST-Link通信电路、24 V直流电源、上位机及其通信模块等组成。系统的总体结构框图如图 3所示。
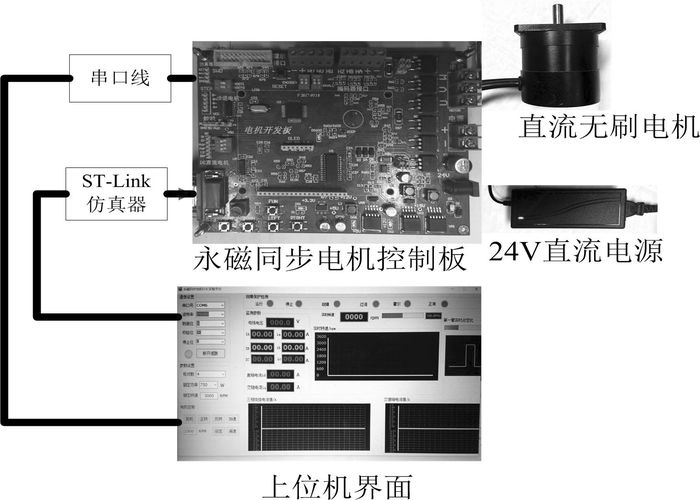 |
| 图 3 直流无刷电机实验平台结构图 |
完成实验平台的搭建后, 接通电源, 启动电机, 通过按键调节设定电机运行速度, 通过上位机实时观测电机运行转速、定子相电流和交直轴电流。对获得的数据进行处理, 得电流波形(图 4、图 5)。
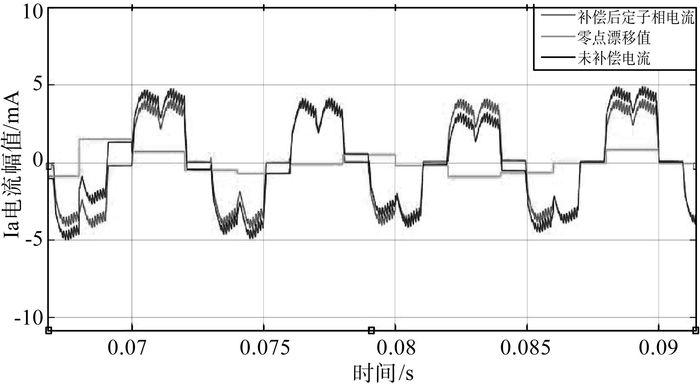 |
| 图 4 iq电流补偿前后波形图 |
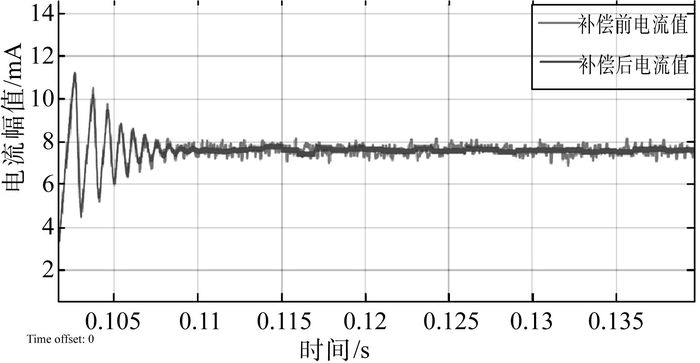 |
| 图 5 iq电流补偿前后波形图 |
根据图 4定子电流波形值可知, 未补偿相电流的幅值会随着电机运行以及环境的变化产生幅值波动。通过对一个周期的相电流进行积分得到电流误差值。对定子电流进行修正得到补偿后的定子相电流。电流波形相对稳定。
根据相电流计算得到两相旋转坐标下电流iq与转矩成正比。电流值可以反映出转矩情况。如图 5所示, 未补偿电流波动明显, 补偿后电流波动减少。证明无硬件在线定子电流零漂补偿有效, 可使系统转矩输出稳定。
4 结论本文首先分析了电机运行过程中运放零漂存在的原因及影响, 提出了无硬件运放零漂在线补偿方法, 最后搭建了实验系统进行测试。通过理论推导和实验证明, 补偿后的电流稳定, 电机转矩脉动小, 可实现无刷直流电机平稳控制。整个系统检测电路简单, 降低了控制成本, 具有较好的实用性。
| [1] |
徐东, 王田苗, 魏洪兴. 一种基于简化模型的永磁同步电机转动惯量辨识和误差补偿[J]. 电工技术学报, 2013, 28(2): 126-131. |
| [2] |
刘晔, 张璐, 杨新伟, 等. 采用硬件神经电路的压力传感器零点温漂补偿研究[J]. 西安交通大学学报, 2010, 44(8): 10-14. DOI:10.7652/xjtuxb201008003 |
| [3] |
VALERO M R, CELMA S, CALVO B, et al. CMOS voltage-to-frequency converter with temperature drift compensation[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(9): 3232-3234. |
| [4] |
李树胜, 付永领, 刘平, 等. 磁悬浮飞轮储能UPS系统集成应用及充放电控制方法研究[J]. 中国电机工程学报, 2017, 37(12): 170-176. |
| [5] |
王秀敏, 徐雅斌, 王中鹏. 集成运算放大器的零漂特性研究[J]. 辽宁工程技术大学学报, 2006, 25(1): 107-110. |
| [6] |
BLANVILLAIN S, VODA A, BESANCON G, et al. Subnanometer positioning and drift compensation with tunneling current[J]. IEEE Transactions on Control Systems Technology, 2013, 22(1): 180-189. |
| [7] |
周二磊, 符晓, 伍小杰, 等. 低定子频率下消除电流测量误差的磁链观测器[J]. 电工技术学报, 2011, 26(6): 67-72. |
| [8] |
WANG W, QIU C. Compensating error of signal conditioning circuit based on least square curve fitting[J]. Computer Measurement & Control, 2009, 17(11): 2246-2248. |
| [9] |
郭必广. 运放失调电压自动补偿设计[J]. 科技信息, 2010(15): 88-89. |
 2017, Vol. 31
2017, Vol. 31


