| KUKA-KR16机器人的运动学分析与仿真 |
伴随着科技的进步, 工业运用中的机器人技术现已达到了比较高的水平。在实际的工业生产运用中KUKA-KR16机器人占据着重要的地位, 而在技术的提高和发展方面, 机器人运动学的部分一直扮演者至关重要的角色, 而在实际的实践中对现成的机器人进行研究会存在成本高, 不容易实现的特点, 因此我们采用MATLAB作为研究平台, 通过MATLAB里面的Robotics Toolbox建立起KUKA-KR16的结构模型[1], 运用Robotics Toolbox来对KUKA-KR16模拟仿真并且可以通过计算机直观的表达出来进行观察理解, 因此能很好的分析KUKA-KR16各个轴的运动状况, 从而对KUKA-KR16机器人做准确的分析与研究。
1 KUKA-KR16机器人运动学模型 1.1 KUKA-KR16机器人结构主体KUKA-KR16是具有六个运动轴的关节机器人, 前3个关节用来确定手腕参考点的位置, 后3个关节用来确定手腕的方位[2], 实现手腕的俯仰、翻滚和偏转[3]。KUKA-KR16的尺寸图如下图 1。
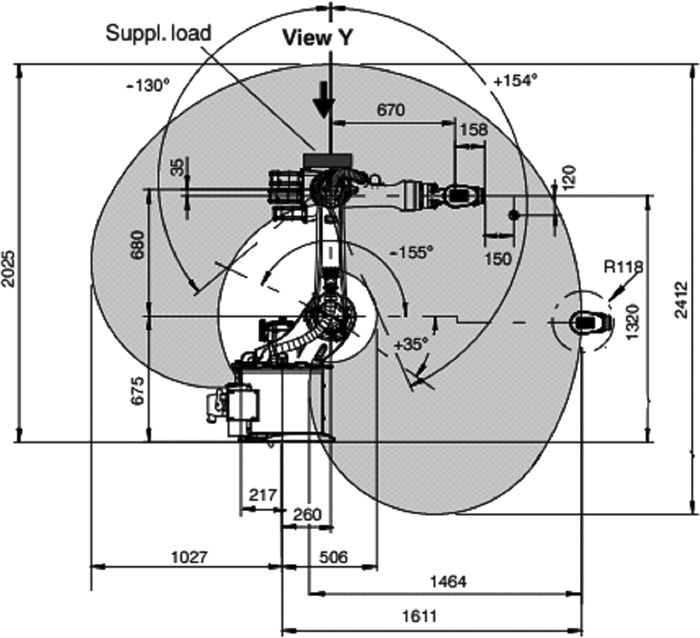 |
| 图 1 KUKA-KR16尺寸图 |
可以从图 1中得到KUKA-KR16每个轴的尺寸, 依据坐标变换准则在每个关节处建立坐标, 由各个连杆之间的连接关系得到相应的连杆参数, 基于坐标变换理论根据以下原则建立坐标系:D-H连杆坐标系的参考坐标系{0}与基座固定连接, 用参考坐标系{0}来表达其余连杆的运动状况[4], 建立的坐标系如图 2所示。
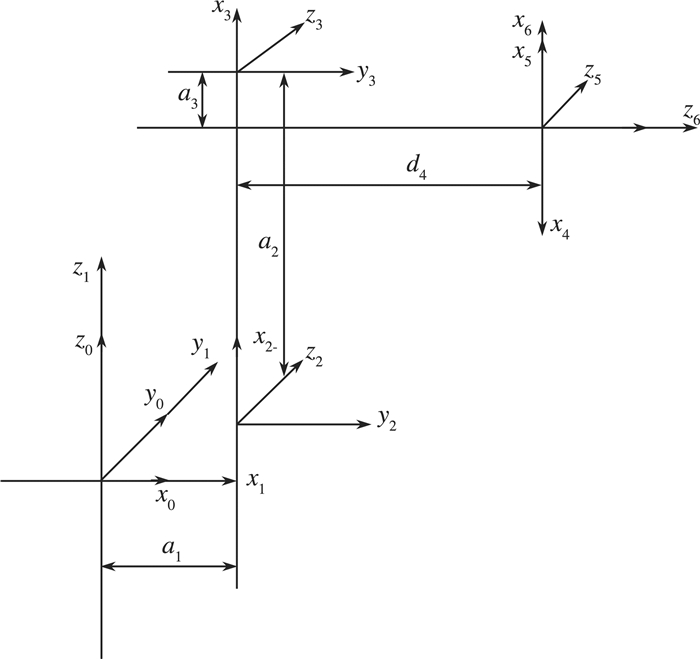 |
| 图 2 连杆坐标系 |
1.2 KUKA-KR16机器人D-H参数
D-H参数法坐标系是由Denavit和Hartenberg于1995提出的一种为关节链中的每一个杆件建立坐标系的矩阵方法[5]。由D-H参数法建立坐标轴原理[6-7]如下:
1) zi坐标轴沿i+1关节的轴线方向;
2) xi坐标轴沿zi和zi-1轴的公垂线, 且指向zi-1的方向;
3) yi坐标轴与xii与zi构成右手坐标系。
另外D-H参数坐标系中各个参数的含义如下:
1) 连杆长度ai:为两关节轴线间的距离;
2) 连杆扭角αi:为两关节轴线间的夹角;
3) 连杆距离di:为两垂线ai与ai-1之间距离;
4) 连杆转角θi:为两垂线ai与ai-1之间的夹角。
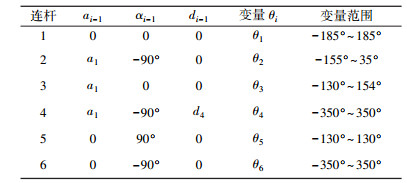
KUKA-KR16机器人是德国库卡公司生产的一种具有高灵活性特点并且可以广泛应用于搬运、组装、机加工等多种领域的六自由度机器人[8], 其D-H参数如下表 3所示。
| 表 1 KUKA-KR16机器人的连杆参数 |
 |
2 KUKA-KR16机器人的运动学分析
工业机器人的运动问题就是为了研究每个轴在空间内的坐标关系, 利用齐次变换且结合D-H参数法求出坐标系之间的转换关系从而建立了运动学方程来分析机器人的各个位姿[9], 也即称为正运动学;相反, 由位姿信息求解所能达到此位姿的相应关节角的过程则为逆运动学。
2.1 KUKA-KR16机器人正运动学问题机器人的正运动学问题也就是为了找出连杆参数之间的联系, 通过矩阵的齐次方程变换求出机器人末端执行器的位姿在基座坐标系中的位姿, 为了更好的表示连杆之间的联系, 不妨设i-1iT为连杆i在i-1坐标系中的位姿, 则根据KUKA-KR16连杆参数和D-H参数法有:
| $ _1^0T = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&{ - \sin {\theta _1}}&0&0\\ {\sin {\theta _1}}&{\cos {\theta _1}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ _2^1T = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _2}}&{ - \sin {\theta _2}}&0&{{a_1}}\\ 0&0&1&0\\ { - \sin {\theta _2}}&{ - \cos {\theta _2}}&0&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ _3^2T = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _3}}&{ - \sin {\theta _3}}&0&{{a_2}}\\ {\sin {\theta _3}}&{\cos {\theta _3}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ _4^3T = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _4}}&{ - \sin {\theta _4}}&0&{{a_3}}\\ 0&0&1&{{d_4}}\\ { - \sin {\theta _4}}&{ - \cos {\theta _4}}&0&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ _5^4T = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _5}}&{ - \sin {\theta _5}}&0&0\\ 0&0&{ - 1}&0\\ {\sin {\theta _5}}&{\cos {\theta _5}}&0&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ _6^5T = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _6}}&{ - \sin {\theta _6}}&0&0\\ 0&0&1&0\\ { - \sin {\theta _6}}&{ - \cos {\theta _6}}&0&0\\ 0&0&0&1 \end{array}} \right] $ |
由KUKA-KR16的相邻两个连杆之间的矩阵关系, 再经过将每一个连杆进行统一计算的过程可以得到总的运动学方程如下:
| $ \begin{array}{l} T = _6^0T = _1^0T\left( {{\theta _1}} \right)_2^1T\left( {{\theta _2}} \right)_3^2T\left( {{\theta _3}} \right)_4^3T\left( {{\theta _4}} \right)_5^4T\\ \left( {{\theta _5}} \right)_6^5T = \left( {{\theta _6}} \right) \end{array} $ |
上式则被称为KUKA-KR16的正运动学方程, 由上面的表达式可以很好的表示KUKA-KR16每个轴间的变换关系, 并且可以根据此方程求出KUKA-KR16机器人的空间位置和姿态的联系, 也就是说实现了KUKA-KR16关节变量组成的关节空间到笛卡尔空间的变换[10]。
2.2 KUKA-KR16机器人逆运动学问题在实际的KUKA-KR16机器人运用中, 一般情况下需要在已知KUKA-KR16目标位姿的情况下求出所需要的参数值, 这就是KUKA-KR16机器人的逆运动学问题。KUKA-KR16机器人具有不同的方式可以求出需要的解, 但是一般来说主要分为封闭和数值两类解法, 而其中的封闭解法的运用较多一些, 具体的求解步骤可以利用封闭解法中的代数法求解, 即用逆阵T1-1左乘并且逐次求解方程, 然后根据矩阵中各个位置元素的相等关系列出等式方程, 从而求出各个未知数, 以此方法进行多次求解直到求出表达式中所有的关节变量, 此类方法也叫做分离变量法。
若在给定的矩阵中, nx, ny, nz, ox, oy, oz, px, py, pz和位姿的值已知, 求解θ1, θ2, θ3, θ4, θ5, θ6, 其中:
| $ {T_1}{T_2}{T_3}{T_4}{T_5}{T_6} = \left[ {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}}\\ {{n_z}}&{{o_z}}&{{a_z}}&{{p_z}}\\ 0&0&0&1 \end{array}} \right] $ |
求解θ1, θ3。用逆矩阵T1-1左乘上式矩阵方程, 整理可以得到如下表达式:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\cos {\theta _1}}&{\sin {\theta _1}}&0&0\\ { - \sin {\theta _1}}&{ - \cos {\theta _1}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {{n_x}}&{{o_x}}&{{a_x}}&{{p_x}}\\ {{n_y}}&{{o_y}}&{{a_y}}&{{p_y}}\\ {{n_z}}&{{o_z}}&{{a_z}}&{{p_z}}\\ 0&0&0&1 \end{array}} \right] = {}^1{T_6} \end{array} $ |
将上式的矩阵展开且化简可得:
| $ - \sin {\theta _1}{p_x} + \cos {\theta _1}{p_y} = {d_2} $ |
解得θ1=arctan2(py, px)
同理可以求出θ2, θ3, θ4, θ5, θ6。
3 基于MATLAB的运动学仿真MATLAB是一种具有强大数学运算功能的仿真编程软件, 在工业产品开发和数值计算分析等方面的教学与研究中是一个十分有效的工具[11]。
在MATLAB平台中, 运用Robotics Toolbox搭建起模型并完成运动学仿真, 主要程序如下。
L1=Link('d', 0, 'a', 0, 'alpha', 0);
L2=Link('d', 0, 'a', 0.5, 'alpha', 0, 'offset', -pi/2);
L3=Link('d', 0, 'a', 0, 'alpha', pi/2, 'offset', 0);
L4=Link('d', 1, 'a', 0, 'alpha', -pi/2);
L5=Link('d', 0, 'a', 0, 'alpha', pi/2);
L6=Link('d', 1, 'a', 0, 'alpha', -pi/2);
robot=SerialLink([L1, L2, L3, L4, L5, L6]);
robot.name='kuka-kr16';
通过在MATLAB运行以上的程序可以得到如下图 4的机器人仿真模型和控制界面, 可以通过滑动控制界面q1, q2, q3, q4, q5, q6对应的滑块按钮控制KUKA-KR16的运动并且可以读出相应位置值和RPY值。
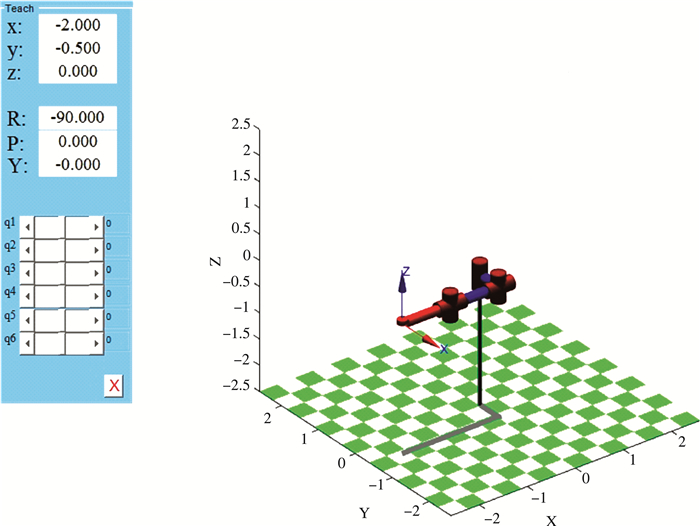 |
| 图 4 MATLAB仿真结构图 |
通过调用plot(q(:, i))、plot(qd(:, i))和plot(qdd(:, i))指令, 可以得到对应轴的位移、速度和加速度曲线[12], 本文通过采用PTP的运动方式来研究KUKA-KR16的运动情况, 假设机器人的起始位置为T0, 起始位置为T1和步数为50ms, 仿真结果如下图 5所示曲线图像, 通过观察轴1关节的图像变化, 可以很好的对其运动状况做出研究, 下图 6为KUKA-KR16的末端执行器在空间内起始位置T0和起始位置T1的运动位移变化。
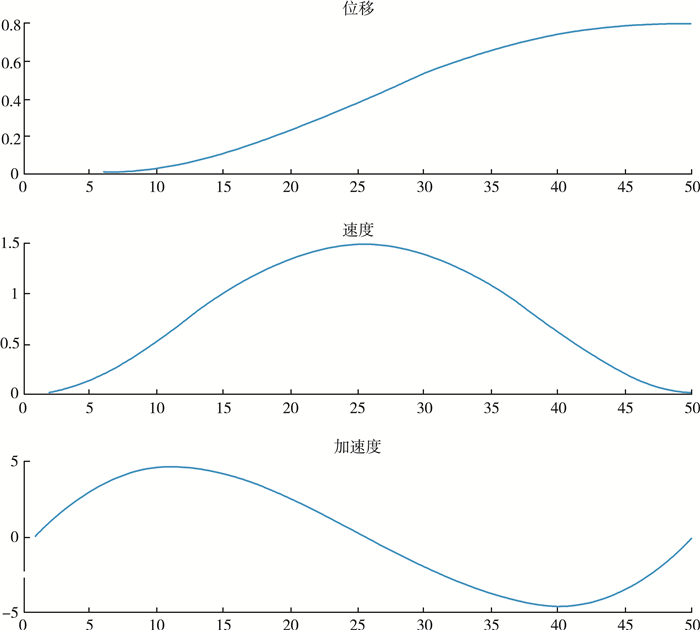 |
| 图 5 仿真结果图 |
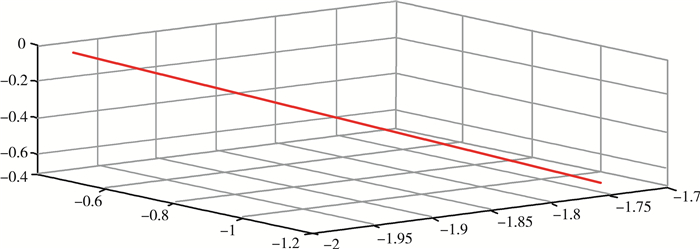 |
| 图 6 T0-T1直线轨迹图 |
4 仿真结果分析
通过控制滑动滑块可以控制机器人各个轴的运动, 从图 4可以看出, 机器人关节的运动情况满足要求, 进而证实了各个连杆参数的设置是合适的, 也可以使末端执行器达到预期的效果。
通过观察图 5中的曲线变化可以得知各个轴运动情况的曲线都是平滑的, 并且在变化的整个过程中没有出现特殊的异常, 则说明KUKA-KR16的速度和加速度在由起始位置T0到达终止位置T1之间的过程中没有出现奇异点。
分析图 6可以得知, KUKA-KR16的末端执行器在起始位置T0和终止位置T1时刻仿真效果和理论的结果不存在偏差, 这表明了KUKA-KR16的PTP动作方式能够使末端执行器到达期望的目标点位姿, 但是在运动的过程中却不能保证各个点的位姿。
5 结束语运动学部分的研究是机器人方面关键的一部分内容, 本文利用MATLAB平台, 在Robotics Toolbox的帮助下, 结合D-H参数法搭建了KUKA-KR16的结构模型, 对KUKA-KR16的正、逆运动学的理论部分进行了仿真验证, 并且MATLAB平台以图形的方式直观的表达了出来, 使为机器人的理论分析和研究提供了很好的理解方式, 加快了对机器人分析研究的步伐。通过本文的理论说明和仿真验证得到的结果为我们后期对机器人进一步的研究提供了良好基础。
| [1] |
SAILONG WU, QIANG Lin, PENG WANG.Kinematics analysis and simulation of KUKA KR5-arc welding robot based on MATLAB.2016 6th International conference on information engineering for mechanics and materials(ICIMM 2016)[C], 中国内蒙古呼和浩特, 2016.
|
| [2] |
钱鹏安, 葛运建.一种基于Puma机器人的三轴线加速度计自动标定方法[C].第五届全国信息获取与处理学术会议, 秦皇岛·北戴河, 2007.
|
| [3] |
李光亮, 陈君若. KUKA KR6机器人的运动学分析与仿真[J]. 自动化仪表, 2018, 39(1): 40-43, 47. |
| [4] |
刘文文. 六自由度工业机器人的动态特性仿真与实验研究[M]. 沈阳: 东北大学, 2014.
|
| [5] |
侯国柱. 关节型机器人的结构设计及其运动学分析[M]. 呼和浩特: 内蒙古工业大学, 2007.
|
| [6] |
蒋新松. 机器人学导论[M]. 沈阳: 辽宁科学技术出版社, 1994.
|
| [7] |
蔡自兴. 机器人学[M]. 北京: 清华大学出版社, 2000.
|
| [8] |
吴晶.基于EMC2的工业机器人研究[D].广州: 华南理工大学, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10561-1011191224.htm
|
| [9] |
王晓强, 王帅军, 刘建亭. 基于MATLAB的IRB2400机器人[J]. 运动学分析, 2014, 42(03): 54-57, 40. |
| [10] |
李骏驰, 李春书. 焊缝打磨机器人的运动学分析与仿真[J]. 河北工业大学学报, 2017, 46(01): 34-39, 47. |
| [11] |
KLAASSEN B, LINNEMANN R, SPENNEBERG D, et al. Biomimetic walking robot SCORPION:control and modeling[J]. Robotics and Autonomous Systems, 2002, 41(2): 69-76. |
| [12] |
薛定宇, 陈阳泉. 基于MATLAN/Simulink的系统仿真技术与应用[M]. 北京: 清华大学出版社, 2002.
|
 2019, Vol. 33
2019, Vol. 33


