| 改进的永磁同步电机转动惯量辨识方法及其在PI自整定中的应用 |
随着现代工业技术的飞速发展,永磁同步电动机(PMSM)因具有简单的结构、强大的过载能力、快速的响应速度以及高效率、高可靠性等优点,在伺服领域中已经占据了重要地位[1]。伴随着PMSM伺服系统的应用变得越来越广泛,人们会不断提高对其性能方面的要求。转动惯量作为PMSM中的一个重要参数,对于电机控制的准确性有着重要的影响:转动惯量的增加,会导致整个系统响应特性的降低;转动惯量的降低,会导致速度响应出现超调甚至震荡现象[2]。
转动惯量的辨识方法可分为两类:一类为离线转动惯量辨识方法,主要有直接计算法、加减速法[3]、人工规划的方法[4];另一类为在线转动惯量辨识方法,主要有最小二乘法[5]、状态观测器法[6]、卡尔曼滤波法[7]、模型参考自适应法[8]。每种方法都有自身的优点和不足。本文对模型参考自适应法进行改进,在该方法的基础上加入参考自适应参数,引入加权递推平均滤波法,对电流进行滤波,减小电流噪声对电磁转矩的影响,提高转动惯量辨识的精确度。
辨识得到的转动惯量与永磁同步电机速度环PI调节相结合,根据转动惯量的取值实时改变PI调节器的比例系数和积分系数,使PI控制器能够在线整定参数,提高了系统的动态性能。
1 永磁同步电机数学模型对于不同的坐标系统,永磁同步电机的数学模型也不同,这里我们选用d-q坐标系统下数学模型[9]。PMSM的机械运动学方程为:
| $ {T_e} - {T_l} = J\frac{{d{\omega _m}}}{{dt}} + D{\omega _m} $ | (1) |
其中J为电机转动惯量,ω为转子机械角速度,D为粘滞摩擦系数,Te为电磁转矩,Tl为负载转矩。
电磁转矩方程为:
| $ {T_e} = 1.5{p_n}[{\varphi _f}{i_q} + \left( {{L_d} - {L_q}} \right){i_d}{i_q}] $ | (2) |
其中pn为电机极对数,φf为永磁体磁链,Ld、id分别为d轴电感和电流,Lq、iq分别为q轴电感和电流。
2 模型参考自适应的转动惯量辨识过程模型参考自适应方法的主要思想是将含有待估计参数的方程作为参考模型,而将不含有未知参数的方程作为可调模型,使得两模型具有相同物理意义的输入量与输出量,从而利用两模型的误差来实时调节可调模型的参数[10],使得最终能够实现可调模型输出跟踪控制对象的输出的目的。其原理如图 1所示。
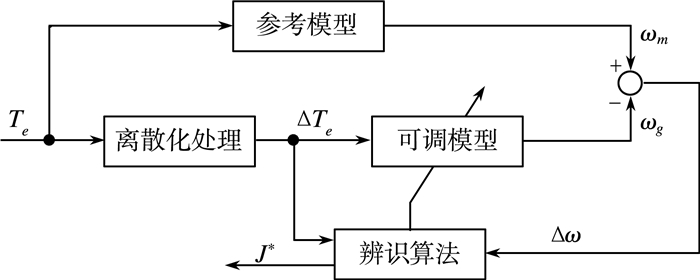 |
| 图 1 参考自适应转动惯量辨识原理 |
由于辨识算法以足够高的采样频率对速度进行采样,所以可忽略摩擦阻力。永磁同步电机的机械运动方程(1)离散化可得:
| $ {T_e}\left( {k - 1} \right) = {T_l}\left( {k - 1} \right) + \frac{J}{{{T_s}}}\left[ {{\omega _m}\left( k \right) - {\omega _m}\left( {k - 1} \right)} \right] $ | (3) |
| $ {T_e}\left( {k - 2} \right) = {T_l}\left( {k - 2} \right) + \frac{J}{{{T_s}}}[{\omega _m}\left( {k - 1} \right) - {\omega _m}(k - 2)] $ | (4) |
辨识算法控制周期较短,实际的电机运行中,负载在一个周期发生剧烈变化的可能性较小。因此,可以认为在一个辨识周期Ts中负载不变,即:
| $ {T_l}\left( {k - 1} \right) = {T_l}(k - 2) $ | (5) |
整理式(3)、式(4)和式(5),得:
| $ {\omega _m}\left( k \right) = 2{\omega _m}\left( {k - 1} \right) - {\omega _m}\left( {k - 2} \right) + \frac{{{T_x}}}{J}[{T_e}\left( {k - 1} \right) - {T_e}(k - 2)] $ | (6) |
令
将式(7)作为参考模型,则可得出可调模型的方程:
| $ {\omega _g}\left( k \right) = 2{\omega _m}\left( {k - 1} \right) - {\omega _m}\left( {k - 2} \right) + {b_g}\Delta {T_e}(k - 1) $ | (8) |
参考模型与可调模型输出的偏差为:
| $ \varepsilon \left( k \right) = {\omega _m}\left( k \right) - {\omega _g}(k) $ | (9) |
根据Landau提出的离散时间迭代参数辨识机制[11],设计自适应算法如下:
| $ {b_g}\left( k \right) = {b_g}\left( {k - 1} \right) + \beta \frac{{\Delta {T_e}\left( {k - 1} \right)}}{{1 + \beta \Delta {T_e}\left( {k - 1} \right)}}\Delta \omega (k) $ | (10) |
β是自适应增益系数,不同的β值对辨识结果有不同的影响,主要表现在收敛速度和波动方面。选取的β值越大,对于转动惯量的辨识速度越快,收敛时间也就越短,但辨识结果会有较大的波动,稳定性差;反之,β值越小,辨识速度越慢,但辨识波动会越小,辨识精度会越高,稳定性强[12]。为了使辨识结果在收敛速度和波动两方面都有显著的效果,需要设计合理的增益系数。
3 变增益系数设计为解决收敛速度和辨识精度冲突的问题,将分段选取不同的自适应增益,根据转动惯量的偏差选取不同的β值。当转动惯量偏差较大时,选取大β值,这样能保证辨识结果快速收敛;当转动惯量的偏差较小时,选取小β值,这样能保证辨识结果波动小、精度高。根据转动惯量的偏差值改变增益系数,能够获得收敛速度快和波动小的辨识结果。上述原理如图 2所示。
 |
| 图 2 变增益系数原理 |
4 加权递推平均滤波过程
通过变增益因子的模型参考自适应法对转动惯量进行辨识,能够获得收敛速度快、辨识精度高的辨识结果,但在实际控制过程中,无法避免噪声产生的影响。为了降低噪声产生的影响,利用加权递推平均滤波法对电流进行滤波。以递推平均滤波法为基础,不同时刻的数据加上不同的权值,得到加权递推平均滤波法,解决了递推平均滤波法灵敏度低的缺点[13]。选取的权系数越大,灵敏度越高,但信号平滑度越低。通过改变权值来改善滤波器的性能。
选取的永磁同步电机的d轴与q轴电感相等,式(2)可简化为:
| $ {T_e}\left( k \right) = 1.5p{\varphi _f}{i_q}(k) $ | (11) |
运用加权递推平均滤波法对d轴电流进行滤波,权值由多次实验得到,则式(11)变为:
 |
(12) |
所以:
 |
(13) |
 |
(14) |
先对电流进行滤波,再进行转动惯量的辨识,这样就能减小噪声对辨识结果的影响。
5 PI参数自整定过程转动惯量影响速度闭环控制。将转动惯量应用于PI参数自整定之中,能够改善伺服系统的控制性能。伺服控制系统一般由外环速度环和内环电流环组成双闭环控制系统[14]。将电流环进行简化,将其看作速度环中的一个环节,这样速度环为带有零点的二阶系统。简化后的速度环等效原理如图 3所示。
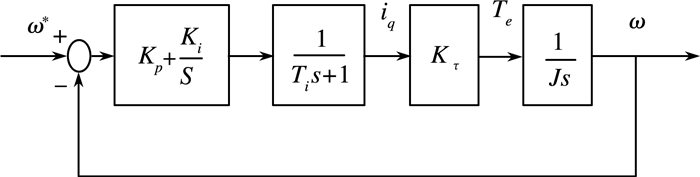 |
| 图 3 速度环等效框图 |
其中ω*为电机的给定转速,Kp为速度环的比例系数,Ki为速度环的积分系数,Ti=L/Rs为电流环的闭环时间常数,Kτ=1.5pn2ψf为电机的转矩系数,J为转动惯量。由速度环等效框图可以得出系统的开环传递函数为:
| $ G\left( s \right) = \frac{{{K_\tau }\left( {{K_p}s + {K_i}} \right)}}{{J{s^2}({T_i}s + 1)}} $ | (15) |
令:
| $ K = \frac{{{K_\tau }{K_i}}}{J}, {T_s} = \frac{{{K_p}}}{{{k_i}}} $ | (16) |
则式(15)为:
| $ G\left( s \right) = \frac{{K\left( {{T_s} + 1} \right)}}{{{s^2}({T_i}s + 1)}} $ | (17) |
从传递函数可以看出,这是一个典型的Ⅱ型系统。设计参数选择公式为:
| $ {T_s} = 和{T_i}, K = \frac{1}{{8{T_i}^2}} $ | (18) |
则:
| $ {K_p} = \frac{{hJ}}{{8{T_i}{K_\tau }}} = \frac{{hJ{R_s}}}{{12L{p_n}^2{\psi _f}}} $ | (19) |
| $ {K_p} = \frac{J}{{8{T_i}{K_\tau }}} = \frac{{J{R_s}^2}}{{12{L^2}{p_n}^2{\psi _f}}} $ | (20) |
对于典型的Ⅱ型系统,综合考虑系统的抗干扰性和稳定性,取h=4。
将识别的转动惯量J代入到式(19)和(20)中,就能得到PI控制器的比例系数和积分系数的补偿值,进而进行系统的PI参数调节。
6 仿真实验结果研究对于改进的永磁同步电机转动惯量辨识方法及其在PI自整定中的应用,运用Matlab/Simulink搭建仿真模型,系统框图如图 4所示。
 |
| 图 4 转动惯量辨识及PI自整定系统框图 |
根据图 4所示的流程,运用Matlab/Simulink进行仿真,得到的系统的仿真模型如图 5所示。
 |
| 图 5 转动惯量辨识及PI自整定系统仿真图 |
图 5中电机选择的参数如下:电阻Rs=1.6 Ω,d轴、q轴电感均为L=6.365 H,磁链ψf=0.1852 Wb,电机极对数pn=2,转动惯量J=0.0001854 kg·m2,转速ωm=500 rad/s。采用直轴为零的控制方式。
我们选取ε=1×10-8。当转动惯量的差值大于ε时,取增益系数β=30;当转动惯量的差值小于ε时,取增益系数β=0.05。结合滤波后的d轴电流进行转动惯量识别,得到转动惯量辨识波形图如图 6所示。我们用恒定β值(β=30和β=0.05)再一次对转动惯量进行辨识,得到转动惯量波形图如图 7所示。将图像放大后,观察滤波对噪声的抑制效果,结果如图 8所示。
 |
| 图 6 改进后转动惯量辨识波形图 |
 |
| 图 7 固定β值转动惯量辨识波形图 |
 |
| 图 8 滤波前后的波形图 |
结合图 6和图 7可以看出:改进后的转动惯量识别方法在收敛速度上能够达到β=30时转动惯量辨识结果的收敛速度,约为0.02 s,比β=0.05时辨识结果的收敛速度提高0.13 s;而在t=0.3 s外界加入扰动后,改进后的转动惯量识别方法辨识结果仅仅有1.6%的误差波动,这与β=0.05时转动惯量的辨识结果误差波动相同,比β=30时辨识结果的误差减少了15.4%。结合图 8可以看出:用加权递推平均滤波法对电流滤波后,能够很好地抑制噪声,减小了噪声对转动惯量辨识的影响。所以改进后的转动惯量辨识方法既能够获得辨识精度和收敛速度两方面的优势,又能减小实际控制过程中噪声的影响,具有收敛速度快、精度高、抗干扰能力强的优点。
将辨识得到的转动惯量运用于速度PI调节中,构成转动惯量PI自整定控制系统,得到电机速度波形图,再与传统PI整定控制系统得到的速度波形图进行比较,结果如图 9所示。
 |
| 图 9 速度波形图 |
由图 9可以看出:与传统的PI整定控制系统相比较,通过转动惯量进行PI自整定的控制系统得到的电机速度波形超调小、响应速度快、精度高。超调越小越能避免电机在起步过程中出现抖动现象,在实际应用中具有重要的意义。
7 结论在模型参考自适应算法的基础上,先利用加权递推平均滤波法对电流进行滤波,再实时改变增益系数,这样就得到了更为精确的转动惯量辨识方法,进而对转动惯量进行识别,最后将得到的转动惯量运用于速度环PI自整定中。
从仿真图中可以看出:利用改进后的辨识方法对转动惯量进行辨识,提高了辨识结果的收敛速度和精度,同时又减少了噪声对控制系统的影响。将转动惯量应用于PI自整定控制系统中,能够减小电机速度产生的超调,同时也提高了响应速度和精度,在实际的控制系统中具有重要的指导意义。
| [1] |
王晓晨. 基于参数识别技术的永磁同步电机矢量控制研究[D]. 沈阳: 沈阳工业大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10142-1015579239.htm
|
| [2] |
黄声华, 吴芳. 永磁交流伺服系统国内外发展概况[J]. 微特电机, 2008(5): 52-61. DOI:10.3969/j.issn.1004-7018.2008.05.016 |
| [3] |
HAN Y R, QIU X, ZHU D M. Inertia identification methods for permanent magnetic AC servo system[J]. Advanced Technology of Electrical Engineering and Energy, 2013, 32(3): 36-41. |
| [4] |
徐东, 王田苗, 魏洪兴. 一种基于简化模型的永磁同步电机转动惯量辨识和误差补偿[J]. 电工技术学报, 2013, 28(2): 126-131. DOI:10.3969/j.issn.1000-6753.2013.02.017 |
| [5] |
XIANG C J, LI C B. Parameter identification of permanent magnet synchronous motor based on RLS[J]. Micro-motors, 2012, 40(2): 30-33. |
| [6] |
DING X Z, ZHANG C R, LI H X, et al. Identification of inertia and state estimation for PMSM[J]. Journal of Shandong University (Engineering Science), 2012, 42(2): 70-77. |
| [7] |
XIA J K, SHEN L J. Inertia identification and controller parameter self-tuning of NC rotary table system[J]. Journal of Shenyang University of Technology, 2008, 30(6): 605-608. |
| [8] |
王庆龙, 张崇巍, 张兴. 基于变结构模型参考自适应系统的永磁同步电机转速辨识[J]. 中国电机工程学报, 2008, 28(9): 71-75. DOI:10.3321/j.issn:0258-8013.2008.09.013 |
| [9] |
顾军. 基于DSP的永磁同步电机无传感器矢量控制系统研究[D]. 南京: 南京航空航天大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10287-2006119127.htm
|
| [10] |
付俊永, 王爽. 伺服系统惯量辨识技术(一)——综述[J]. 伺服控制, 2015(2): 66-69. |
| [11] |
LANDAU I D. Adaptive Control[M]. New York: Springer, 1998.
|
| [12] |
钟义长, 钟伦珑. 永磁同步电动机双闭环参数辨识自适应控制[J]. 微特电子, 2012(4): 47-50. |
| [13] |
郝传光. 三维柔性触觉传感器的信息提取与分析[D]. 合肥: 中国科学技术大学, 2010.
|
| [14] |
马立新, 徐镇乾. PI自整定永磁伺服系统转动惯量的辨识研究[J]. 机电工程, 2015(8): 1128-1131. |
 2018, Vol. 32
2018, Vol. 32


