| 基于动态因子增强模型平均方法的股票价格预测 |
股票市场被视为国家经济的晴雨表, 在一定程度上可以直接反映国家的经济状况, 因而股票价格预测得到了许多学者的关注。有效的股票价格预测, 不仅可以指导投资者行为, 而且还可以考察金融风险波动, 促进经济社会平衡发展。
国内外学者在股票价格预测的模型和方法上做了很多尝试。时间序列方法首先被广泛的应用至股票价格预测领域[1-3]。但是, 时间序列模型输入数据的形式比较单一, 且对数据有相对严苛的前提条件, 因此预测能力较为有限。伴随着数据挖掘等新兴技术的发展, 以数据挖掘为基础的方法受到越来越多经济学者们的青睐, 被广泛应用于金融领域的研究[4-5]。贺毅岳等[6]利用自适应噪声完备集合经验模态分解和长短期记忆网络方法对5个代表性股票价格指数进行预测, 结果表明该方法的预测表现较好。但相对而言, 长短期记忆网络模型在金融领域的应用尚不丰富。鉴于统计学的分析方法和基于数据挖掘技术的分析方法各有其优缺点, 越来越多学者在模型选择的不确定性问题上开始关注模型平均的方法。
近年来, 模型平均方法被快速地应用于统计学和计量经济学等领域。模型平均是用一定的权重对来自不同模型的预测进行组合, 减少信息损失, 获得更为稳健的估计[7-8]。模型平均方法主要有两个发展方向: BMA(Bayesian Model Averaging, 贝叶斯模型平均)和FMA(Frequentist Model Averaging, 频率模型平均)。由于BMA方法各子模型的先验概率难以确定, FMA近些年来受到越来越多的关注, 本文主要使用FMA方法进行估计建模。在FMA方法的研究中, 最核心的问题就是组合权重的选择。根据权重选择的准则不同, FMA可以分为Hansen[9]提出的基于Mallows准则的模型平均方法(MMA)以及Hansen和Racine[10]提出的基于删组交叉验证准则的模型平均方法。FMA方法后续被广泛的应用至各个领域[11-16]。
因子增强型回归在高维问题研究中得到越来越多的关注。当解释变量的数目较多时, 假设存在一些潜在的公共因子可以解释原解释变量一定比例的变差, 这时用公共因子进行回归可以在保证预测精度的同时显著降低维数, 提高计算效率。在实际应用中, Forni等[17]创新性地将动态因子增强回归模型应用到欧盟的联合指数预测中。实证研究表明, 当时期数和横截面指标数量趋于无穷时, 动态因子增强回归量是收敛的。在模型平均中, 不同的子模型包含了原解释变量的各种组合, 使用潜在因子代替原解释变量构建子模型会大大简化模型估计。而Xu和Hansen[18]证明了即使存在生成的因子时, MMA估计量是渐近无偏的。同时考察了删组交叉验证准则, 结果显示在条件异方差存在的情形下, 删组交叉验证准则模型平均估计量也是渐近无偏的。为因子增强与模型平均方法的结合使用提供了理论依据。
受以上文献启发, 本文区别于使用时间序列和数据挖掘方法的单一模型, 而是基于动态因子增强型模型平均方法对上证综指的日收盘价序列进行预测。具体地, 在使用因子增强与模型平均方法结合时, 提取出合理的公因子个数而不是将其看做未知参数, 简化参数估计。首先提取出原始变量不可观测的公共因子, 在此基础上使用模型平均方法进行预测。将基于不同准则的模型平均预测结果对比分析。结果表明, 动态因子增强型删组交叉验证准则模型平均方法的预测效果更好。
1 理论模型 1.1 模型表示本文参考Xu和Hansen[18]的思路。用yt和Xit分别表示被解释变量和解释变量, 其中t, i分别表示第t期变量和第i个解释变量, 0≤t≤T, 0≤i≤N。被解释变量的向前h步预测模型可以表示为公式(1):
| $ \begin{gathered} y_{t+h}=\alpha_0+\alpha(L) y_t+\beta(L)^{\prime} F_t+\varepsilon_{t+h}, \\ X_{i t}=\lambda_i{ }^{\prime} F_t+e_{i t}, \end{gathered} $ | (1) |
其中, α(L)和β(L)分别为p阶和q阶滞后算子多项式, 0≤p≤pmax, 0≤q≤qmax。Ft∈
yt和Ft的最大滞后项阶数分别为pmax和qmax。因此公式(1)概括的最全面回归变量集合为:
| $ z_t=\left(1, y_t, \cdots, y_{t-p_{\max }}, F_t^{\prime}, \cdots, F_{t-q_{\max }}{ }^{\prime}\right)^{\prime} 。$ |
公式(1)可以简化为: yt+h=zt′b+εt+h, 系数矩阵b包含公式(1)中的所有待估计参数。把zt的第m个子集表示为zt(m), 0≤m≤M, 则第m个近似估计模型为:
| $ y_{t+h}=z_t(m)^{\prime} b(m)+\varepsilon_{t+h}(m) \text { 或矩阵形式: } y=Z(m) b(m)+\varepsilon(m)。$ |
在本文中, 不对近似估计模型的估计变量做任何的限制。它可能包含所有的公共因子及其滞后项, 也可能不包含任何公共因子。子模型的选择需要采取在实证和计算中都切实可行的方法, 由于不能确定包含哪些解释变量时会得到更好的预测效果, 我们使用的是连续嵌套的方法, 以此保证子模型集合中包含解释变量组合的所有可能性。即: 第一个子模型包含的解释变量集合zt(1)=(1), 第二个子模型包含的解释变量集合zt(2)=(1, yt), …。对于最大滞后项阶数pmax和qmax, 备选的子模型个数为M=1+(pmax+1)+r×(qmax+1)。
在实际的分析中, 用估计的公共因子
综上, 对于第m个近似估计模型, 可以得到一个yT+h的估计值:
| $ \hat{y}_{T+h \mid T(m)}=\tilde{z}_T(m)^{\prime} \hat{b}(m)。$ |
模型平均方法即对每一个子模型估计值进行加权组合。经过加权后yT+h的估计值为:
| $ \hat{y}_{T+h \mid T(w)}=\sum_{m=1}^M w_m \hat{y}_{T+h \mid T(m)}, $ |
其中, wm为满足以下条件的组合权重:
| $ H^M=\left\{\left(w_1, \cdots, w_M\right) \mid 0 \leqslant w_m \leqslant 1, \sum_{m=1}^M w_m=1\right\} 。$ |
对不可观测的因子Ft, 本文使用因子分析法进行估计: 前r个因子即为矩阵XX′/(TN)由大到小前r个特征值对应的特征向量(乘以T1/2)。
对于第m个近似估计模型y=Z(m)b(m)+ε(m), b(m)的最小二乘估计量可以表示为
| $ \hat{\varepsilon}_{t+h}(w)=\sum_{m=1}^M w_m \hat{\varepsilon}_{t+h}(m)。$ |
令k(m)=dim(zt(m))为第m个子模型中回归变量的个数。Mallows准则可以表示为:
| $ \mathrm{C}_T(m)=\left(\sum\limits_{t=1}^T \hat{\varepsilon}_t(m)^2+2 \hat{\sigma}_T^2 \times k(m)\right) / T_{。} $ |
其中
为使
| $ \hat{\sigma}_T^2=(T-k(M))^{-1} \sum_{t=1}^T \hat{\varepsilon}_t(M)^2 。$ |
模型选择是从M个子模型中选择一个最优模型, 因此模型选择可以看做是模型平均的一个特殊情况: 选择第j个子模型, 那么wm=1。若基于Mallows准则进行模型选择(记为MMS), 选择的模型为满足以下条件的第
对于模型平均, 基于Mallows的模型平均权重选择准则为:
| $ \mathrm{C}_T(w)=\left(\sum\limits_{t=1}^T\left(\sum\limits_{m=1}^M w_m \hat{\varepsilon}_t(m)\right)^2+2 \hat{\sigma}_T^2 \times \sum\limits_{m=1}^M w_m k(m)\right) / T 。$ | (2) |
MMA就是选择使得CT(w)达到最小的权重, 即
| $ \hat{w}=\operatorname{argmin}_{w \in \mathrm{H}^M} C_T(w)。$ |
从公式(2)可以看出, CT(w)是权重向量的二次函数, 因此
Hansen和Racine [10]指出, MMA要求误差项是同方差且不存在序列相关的。误差的同方差限制可以通过使用删一的交叉验证准则来避免, 即JMA方法。
1.3.2 基于交叉验证准则为比较简便的表述这一准则, 首先将删组交叉验证的预测误差表示为
删组交叉验证预测误差向量
| $ \tilde{\varepsilon}_{t+h, h}(m)=\hat{\varepsilon}_{t+h}(m)+\tilde{z}_t^{\prime}(m)\left(\sum\limits_{|j-t| \geqslant h} \tilde{z}_j(m) \tilde{z}_j^{\prime}(m)\right)^{-1} \times\left(\sum\limits_{|j-t|<h} \tilde{z}_j(m) \hat{\varepsilon}_{j+h}(m)\right) 。$ |
基于删组交叉验证的模型平均权重选择准则(记为hMA)为:
| $ \mathrm{CV}_{h, T}(w)=\left(\sum\limits_{t=1}^T \tilde{\varepsilon}_{t+h, h}(w)^2\right) / T=\left(\sum\limits_{t=1}^T\left(\sum\limits_{m=1}^M w_m \tilde{\varepsilon}_{t+h, h}(m)\right)^2\right) / T 。$ |
hMA就是选择使得CVh, T(w)达到最小的权重, 即
| $ \operatorname{CV}(\hat{w})=\operatorname{argmin}_{w \in \mathrm{H}^M} C \mathrm{~V}_{h, T}(w) 。$ |
从公式(3)可以看出, CVh, T(w)是权重向量的二次函数, 因此CV(
当h=1时, 为删一的交叉验证准则, 在统计学中删一的交叉验证又称为Jackknife, 故Jackknife准则(记为JMA)的预测误差
| $ \tilde{\varepsilon}_{t+h, 1}(m)=\hat{\varepsilon}_{t+h}(m)\left(1-\tilde{z}_t(m)^{\prime}\left(\tilde{Z}(m)^{\prime} \tilde{Z}(m)\right)^{-1} \tilde{z}_t(m)\right)^{-1} 。$ |
Hansen和Racine [10]指出, JMA方法虽然解除了误差项是同方差的限制, 但仍然要求误差项是序列不相关的。当h>1时, 误差项εt+h是移动平均过程, 因此是序列相关的。此时使用h>1的删组交叉验证准则即CVh, T(w)(h>1)可以消除序列不相关的限制。
Xu和Hansen[18]证明了存在生成的因子时, 由于生成的因子在增大参数估计值均方误差的同时, 会同步增大各项准则值, 所以上文提到的各模型平均估计量仍然是渐近无偏的。
1.3.3 基于简单平均在本文中, 为了对比各方法的预测效果, 加入了简单模型平均的内容。将简单模型平均方法记为SMA, SMA的子模型权重S(
各评价指标中, Yt表示真实值,
(1) 平均绝对误差(Mean Absolute Error, MAE)
| $ \text { MAE }=\left(\sum\limits_{t=1}^T\left|\hat{Y}_t-Y_t\right|\right) / T_{。} $ |
(2) 均方根误差(Root Mean Square Error, RMSE)
| $ \operatorname{RMSE}=\left(\left(\sum\limits_{t=1}^T\left(\hat{Y}_t-Y_t\right)^2\right) / T\right)^{1 / 2} 。$ |
(3) 平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)
| $ \operatorname{MAPE}=\left(\sum\limits_{t=1}^T \frac{\left|\hat{Y}_t-Y_t\right|}{Y_t}\right) / T \times 100 \% \text { 。} $ |
(4) 最优率
在其他条件相同的情况下, 把预测误差最小的模型称为该条件下的最优模型。最优率即模型最优次数与分类条件总数的比值。
(5) Diebold-Mariano检验法
除了上述评价指标, 本文运用Diebold和Mariano [19]提出的DM检验法进一步研究动态因子增强删组交叉验证模型平均方法与参照预测模型间是否存在显著差异。
DM检验的原假设为模型a和模型b的预测能力没有显著差异, 相应的统计量为:
| $ \begin{gathered} \mathrm{DM}=\bar{d} /\left(\left(\gamma_0+2 \sum\nolimits_{l=1}^{h-1} \gamma_l\right) / n\right)^{1 / 2}, \\ \bar{d}=\sum\nolimits_{l=1}^n d_i / n, \gamma_l=\sum\nolimits_{i=l+1}^n\left(d_i-\bar{d}\right)\left(d_{i-l}-\bar{d}\right) / n, \end{gathered} $ |
其中, d表示两个模型预测误差的平均差距, ei, 1和ei, 2分别表示模型a的预测误差和模型b的第i项预测误差, 则di=|ei, 1|-|ei, 2|。另外, γl是l阶自协方差的估计值, k是自相关阶数。本文中, DM检验法中的预测误差用MAE来衡量。
对于前四项评价指标, MAE、RMSE、MAPE值越小, 预测误差越小, 模型预测表现越优;最优率越高, 模型预测表现越优;在DM检验中, 当ei, 1和ei, 2分别表示模型a的预测误差和模型b的预测误差, di=|ei, 1|-|ei, 2|时, DM值大于0表示模型b更优, DM值小于0表示模型b更优。
2 实证研究本节中我们将动态因子增强型模型选择和动态因子增强型模型平均方法: MMA、MMS、JMA、hMA和SMA应用于上证综指的日收盘价预测。
2.1 数据与分析本文数据来自网易财经网站(https://money.163.com/), 样本区间从2017年1月3日至2021年7月14日。被解释变量是日收盘价, 原始解释变量包括最高价、最低价、开盘价、前收盘、涨跌额、涨跌幅、成交量和成交金额。
首先, 绘制上证综指日收盘价的时间序列图。从图 1可以看出, 样本区间内数据趋势有明显的波动, 总体呈现出先下降后上升的趋势。
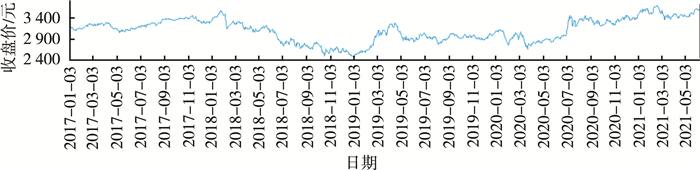 |
| 图 1 上证综指日收盘价时序图 |
其次, 对数据进行描述性统计分析、正态性检验以及平稳性检验, 结果如表 1所示。从表 1可以看出, 数据偏度系数为负, 偏度检验也显示偏态系数显著不等于0, 数据分布是非对称的;峰度系数小于3, 峰度检验显示峰度系数显著不等于3, 数据分布比正态分布更平。J-B检验的结果非常显著, 表明序列不服从正态分布。对原始数据进行ADF检验, 统计量值为-1.622, p为0.738, 无充分理由拒绝数据非平稳的原假设, 表明原始数据非平稳。
| 表 1 上证综指日收盘价描述性统计 |
 |
考虑到上述模型中解释变量包含有被解释变量的各阶滞后项, 为了提高预测精度, 对原始数据进行一阶差分处理。再对数据进行ADF平稳性检验, p为0.01, 表明差分后的数据是平稳的。
因此, 把进行一阶差分后的日收盘价数据看作是输入的被解释变量yt, 为了保持数据在时间上的一致性, 对各个原始解释变量均进行一阶差分操作, 将其作为原解释变量, 定义为X1-X8, 以此建立各模型。
2.2 模型比较对原解释变量做因子分析, 结果表明提取如下3个公共因子是比较合理的。方差解释表如表 2所示, 前3个公共因子分别解释了X1-X834%、34%和27%的变差, 累计可以解释X1-X895%的变差, 拟合效果较好:
| 表 2 方差解释表 |
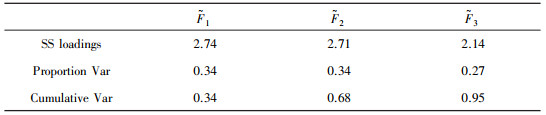 |
这3个公共因子可以用原始变量表示为:
| $ \tilde{F}_1=0.846 X_1+0.945 X_2+0.852 X_3+0.588 X_4+0.102 X_7+0.166 X_8 \text {, } $ |
| $ \begin{aligned} &\tilde{F}_2=0.140 X_1-0.387 X_3-0.746 X_4+0.944 X_5+0.944 X_6, \\ &\tilde{F}_3=0.422 X_1+0.185 X_3+0.136 X_4+0.979 X_7+0.972 X_{8}。\end{aligned} $ |
在实际的拟合过程中, 使被解释变量yt和各公共因子的最大滞后阶数相等, 设为pmax, 此时可能的子模型个数为M=1+(r×1)×(pmax+1)。针对不同的滞后阶数pmax与预测步长h, 对各个模型的预测效果进行分析。
图 2是在不同的最大滞后阶数pmax下, 不同方法的MAE指标随预测步长h的变化情况。pmax=0时, 只有当预测步长为4时, MMS方法才优于其他模型平均方法;同时也可以看出, MMS的预测误差波动较为平缓, 因为pmax=0时, 可供选择的子模型数量仅有4个, 选择空间较小, 而模型平均可以通过调整权重大小改变估计系数。
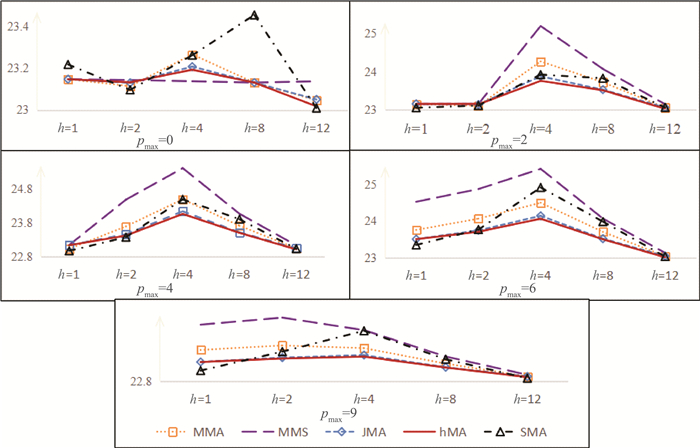 |
| 图 2 不同方法预测结果 |
在pmax≠0时, 模型选择方法不优于模型平均方法。从短期预测的效果来看, 最大滞后阶数pmax较小时各模型的预测效果相对集中。随着pmax的增大, 各模型的预测效果逐渐离散化。在预测步长h=4时, 各方法预测误差的分布最为离散, hMA方法的预测优势最为突出。当最大滞后阶数pmax≠0时, hMA方法的MAE值均略小于其他方法的MAE值, 对应的折线位于其他方法对应的直线下方。RMSE值与MAPE值在不同的最大滞后阶数pmax下随预测步长h的变化情况与MAE值大致相同, 在此不再赘述。
表 3给出了不同评价指标下各方法的最优率。从表 3中可以看出, 在评价指标为MAE的情况下, 最优率排名前三的模型为hMA、SMA和MMS模型;在评价指标为RMSE情况下, 最优率排名前三的模型为hMA、MMS和SMA模型;在评价指标为MAPE的情况下, 最优率排名前三的模型为hMA、SMA和JMA模型。在各个评价指标下, 最优率最高的方法均是hMA方法。
| 表 3 模型最优率 |
 |
为了对比最优率最高的三种模型的误差分布情况, 图 3给出了hMA、SMA和MMS方法在不同最大滞后阶数pmax下的误差箱线图。从误差箱线图可以看出, 虽然SMA和MMS方法在某些情况下存在最优的可能性, 但是hMA方法的误差分布更为集中, 稳健性更好。
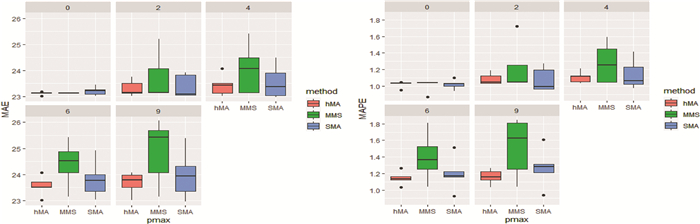 |
| 图 3 误差分布箱线图 |
更进一步地, 为了对比动态因子增强模型选择和各动态因子增强模型平均预测效果的优劣性, 使用DM检验考察不同模型是否存在显著差异。根据前文内容, 当DM值大于0时模型b更优, DM值小于0时模型b更优。从表 4中可以看出:1)模型平均方法显著优于模型选择方法, 2)hMA方法显著优于其他模型平均方法。这与前文所得结论是一致的。
| 表 4 各模型DM检验 |
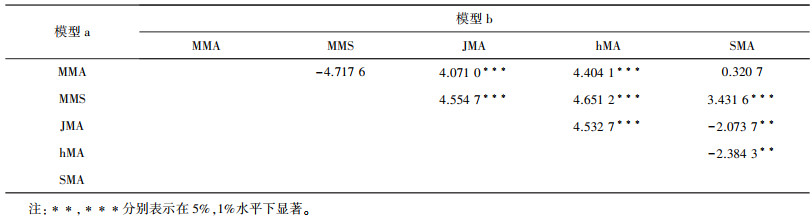 |
2.3 稳健性检验
为了进行未经过差分模型和经过差分模型预测能力的比较, 利用DM检验进行。表 5说明了在不同的预测步长h下, 两模型的DM检验结果。由表 5可知, 经过差分之后的模型在预测步长为2、4、8、12时均通过了对未经过差分模型的DM检验, 即前者的预测效果优于后者。在预测步长为1时, 两模型没有显著差异, 但DM值仍是大于0的。这表明当预测步长为1时, 数据不平稳对预测造成的影响没有多步预测时大。证明了在含解释变量的因子增强型模型平均方法中, 对变量进行一阶差分, 使得被解释变量平稳, 会显著提高模型预测精度。
| 表 5 模型DM检验 |
 |
3 研究结论
当前环境下, 股票市场的变动对国家经济发展有着极其重要的影响, 因此股票价格指数预测具有十分重要的地位。本文将动态因子增强删组交叉验证模型平均应用至上证综指的日收盘价预测中, 通过加权子模型的预测结果, 提高了上证综指日收盘价预测的准确度。
本文结合上证综指日收盘价这一具体场景, 将2017年1月3日至2021年7月14日的上证综指数据作为原始数据集, 详细地介绍了模型平均方法的理论与应用, 并通过各项预测误差指标和DM检验评估其与参照预测模型的预测能力。研究结果表明, 各动态因子增强模型平均的预测效果显著优于动态因子增强模型选择预测效果;在动态因子增强模型平均方法中, 以删组交叉验证模型平均为最优。利用此模型对上证综指日收盘价进行预测是有效的, 可以为投资者决策提供一定参考意见。
| [1] |
CAGINALP G, CONSTANTINE G. Statistical inference and modelling of momentum in stock prices[J]. Applied Mathematical Finance, 1995, 2(4): 225-242. DOI:10.1080/13504869500000012 |
| [2] |
谢赤, 喻欣欣, 李双飞. 双重上市公司A+H股价差时间序列描述与趋势预测[J]. 当代财经, 2008(5): 57-60. |
| [3] |
方燕, 耿雪洋, 秦珊珊. 沪深两市传媒板块指数价格预测研究: 基于ARIMA-GARCH模型的分析[J]. 价格理论与实践, 2018(1): 102-105. |
| [4] |
KIMOTO T, ASAKAWA K. Stock market prediction system with modular neural networks[C]// IJCNN. International Joint Conference on Neural Networks, San Diego, USA, 1990.
|
| [5] |
ZHANG G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing, 2003, 50: 159-175. DOI:10.1016/S0925-2312(01)00702-0 |
| [6] |
贺毅岳, 李萍, 韩进博. 基于CEEMDAN-LSTM的股票市场指数预测建模研究[J]. 统计与信息论坛, 2020, 35(6): 34-45. |
| [7] |
BATES J M, GRANGER C W J. The combination of forecasts[J]. Operational Research Quarterly, 1969, 20(4): 451-468. DOI:10.1057/jors.1969.103 |
| [8] |
YUAN Z, YANG Y. Combining linear regression models: when and how[J]. Journal of the American Statistical Association, 2005(4): 1202-1214. |
| [9] |
HANSEN B E. Least squares model averaging[J]. Econometrica, 2007, 75(4): 1175-1189. DOI:10.1111/j.1468-0262.2007.00785.x |
| [10] |
HANSEN B E, RACINE J S. Jackknife model averaging[J]. Journal of Econometrics, 2012, 167(1): 38-46. DOI:10.1016/j.jeconom.2011.06.019 |
| [11] |
张新雨, 邹国华. 模型平均方法及其在预测中的应用[J]. 统计研究, 2011, 28(6): 97-102. |
| [12] |
赵国庆, 姚青松, 刘庆丰. GARCH族的模型平均估计方法[J]. 数量经济技术经济研究, 2017, 34(6): 104-118. |
| [13] |
李莉莉, 崔迎鹏, 卢睿, 等. 基于模型平均方法的基金绩效预测研究[J]. 系统科学与数学, 2018, 38(6): 711-724. |
| [14] |
LIAO J, ZOU G H, GAO Y. et al, Model averaging prediction for time series models with a diverging number of parameters[J]. Journal of Econometrics, 2020, 223: 190-221. |
| [15] |
LIU Q F, YAO Q S, ZHAO G Q. Model averaging estimation for conditional volatility models with an application to stock market volatility forecast[J]. Journal of Forecasting, 2020, 39(5): 1-53. |
| [16] |
张新雨. 基于最小二乘近似的模型平均方法[J]. 中国科学: 数学, 2021, 51(3): 535-548. |
| [17] |
FORNI M, HALLIN M, LIPPI M, et al. The generalized dynamic-factor model: identification and estimation[J]. The Review of Economics and Statistics, 2000, 82(4): 540-554. |
| [18] |
XU C, HANSEN B E. Forecasting with factor-augmented regression: a frequentist model averaging approach[J]. Journal of Econometrics, 2015(2): 280-293. |
| [19] |
DIEBOLD F X, MARIANO R S. Comparing predictive accuracy[J]. Journal of Business and Economic Statistics, 2002, 20(1): 134-144. |
 2022, Vol. 36
2022, Vol. 36


