| 聚乙二醇@聚(单宁酸-己二胺)的制备及其吸附性能的研究 |
染料和颜料被广泛用作着色剂。每年全世界纺织工业的染料消费总量超过一万吨,并且有大约一百吨染料通过纺织工业被排放到污水中。染料废水是一种包含对微生物种群有毒性作用的化学物质的废弃物,而且对哺乳动物和其他生物体都具有毒性和致癌性[1]。阴离子活性染料广泛应用于皮革、造纸、纺织以及食品等行业[2]。刚果红即为一种阴离子染料,已知其可以引起过敏反应并且可以在人体内代谢产生联苯胺的致癌物[3],因此需谨慎对待其排放与处理。除了高稳定性和毒性,染料对光和温和的氧化剂也有抵抗性,因此它们不能用常规的生物处理过程去除,比如活性污泥和厌氧消化[4]。用于去除污水中的染料的技术有很多,包括吸附法、絮凝沉淀法、高级氧化技术、臭氧处理、膜过滤和生物降解法[5]。吸附法是当前应用最广泛的污水处理方式,与其他方式相比,具有高效、简单、易于回收和再利用的优点[4]。
微胶囊是通过成膜物质将囊内空间与囊外空间隔离开以形成特定几何结构的物质,其内部可以是填充的,也可以是中空的[6]。微胶囊的技术特色在于囊内空间与囊外空间隔离,因而可以分别对囊内和囊外空间的物理化学性质进行调节[7]。聚合物微胶囊在药物封装和释放、人造细胞、催化、化学传感器等领域具有广阔的应用前景,因而得到国内外研究者的广泛关注[8]。本文以聚单宁酸-己二胺(PTHA)为囊壁,以聚乙二醇(PEG)为囊芯,制备了球形完整、粒径均匀、平均粒径在几十到几百纳米的聚乙二醇@聚(单宁酸-己二胺)微胶囊(以下简称PEG@PTHA),并用于水溶液中刚果红的吸附性能的研究。
1 材料与方法 1.1 药品与仪器主要药品包括:聚乙二醇(AR,麦克林);单宁酸(AR,阿拉丁);1, 6-己二胺(AR,阿拉丁);刚果红(AR,麦克林);无水乙醇(AR,天津富宇);去离子水(自制,电阻率18.25 MΩ·cm)。
主要仪器如表 1所示。
| 表 1 主要仪器 |
 |
1.2 PEG@PTHA的制备
称取0.2 g PEG,在100 mL去离子水中分散10 min。将0.4 g单宁酸(TA)溶于100 mL去离子水。将上述两溶液混合,室温下电磁搅拌30 min,溶液迅速变为乳白色。将溶有1, 6-己二胺(HA)0.34 g的100 mL去离子水缓慢加入到上述乳白色溶液中,体系迅速变为深褐色。室温下继续搅拌,反应72 h后,将产物离心处理并用去离子水洗涤多次以去除未反应的单宁酸和己二胺。冷冻干燥12 h,取出研细后保存于样品袋中备用。
1.3 吸附实验为探究合成吸附剂在不同因素的影响下的吸附结果,进行了单因素实验。取一定量吸附剂,放入装有50 mL某初始浓度染料溶液的锥形瓶中,置于恒温振荡器中,于180 r/min转速下震荡一定时间后取下。取一定量溶液进行离心处理,用紫外分光光度计在498 nm处测剩余刚果红(图 1)溶液浓度。本次实验探究了吸附剂在时间(0~48 h)、初始离子浓度(50~250 mg/L)外界条件变化下的吸附效果,并探究其吸附机理。
PEG@PTHA对刚果红的吸附量用下式计算[9]:
| $ {Q_e} = \frac{{({C_0} - {C_e})V}}{m} $ | (1) |
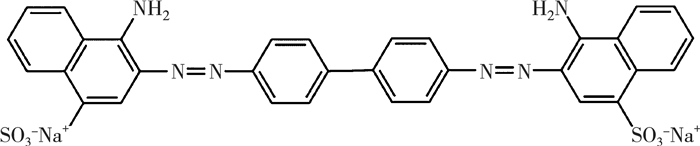 |
| 图 1 刚果红分子结构 |
式中:Qe为平衡时吸附剂的吸附量(mg/g);C0为刚果红初始浓度(mg/L);Ce为吸附平衡时剩余刚果红浓度(mg/L);V为刚果红溶液体积(L);m为吸附剂投加量(g)。
2 结果与讨论 2.1 微胶囊制备机理聚乙二醇含有大量醚键,单宁酸含有大量酚羟基,由于氢键作用,形成聚电解质复合物。聚电解质复合物形成后,聚乙二醇亲水性降低,复合物体系基于单宁酸的立体结构,倾向于形成聚乙二醇在内、单宁酸在外的球形结构。己二胺加入后,由于氢键作用,附着于单宁酸表面,并与后者发生迈克尔加成或席夫碱反应,最终形成以PEG为核、PTHA为壳的微胶囊。PEG@PTHA的制备机理如图 2所示。
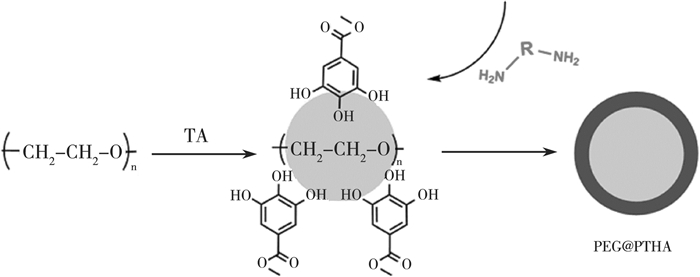 |
| 图 2 PEG@PTHA制备机理 |
2.2 微胶囊的表征
图 3为PEG@PTHA的透射电镜图。由图 3可知,其平均粒径约为200 nm,球形完整,核-壳结构明显。通过透射电镜可以很明显地看出囊壁很好地包覆在囊芯上,颗粒表面较粗糙,有利于吸附染料分子。
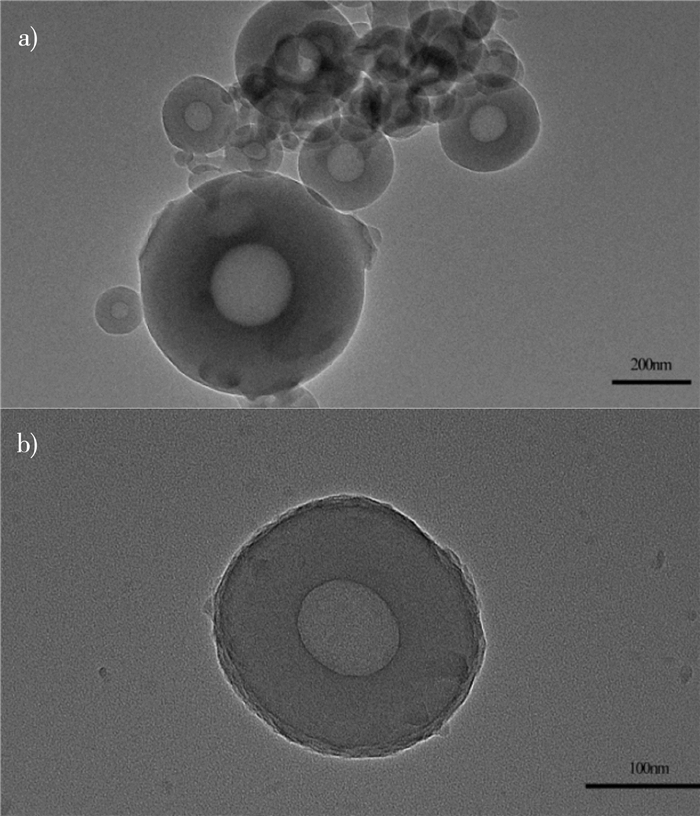 |
| 图 3 PEG@PTHA的透射电镜图 |
图 4(a)为用傅里叶红外光谱仪表征PEG@PTHA的结果。聚乙二醇曲线上1 080~1 150 cm-1处为C-O-C的伸缩振动,而样品1 035~1 140 cm-1处有一短的宽峰;2 940 cm-1和2 840 cm-1处为位于己二胺的烷基链上的C-H的两个伸缩振动峰,在样品相同位置有两个小的吸收峰;样品3 350~3 550 cm-1处出现了一个宽峰,主要由单宁酸、己二胺分别提供的-OH、-NH伸缩振动产生,样品1 710 cm-1、1 600 cm-1处分别为C=O键、苯环振动形成的尖峰,对应单宁酸上的基团。通过以上对比可以推测聚乙二醇、单宁酸、己二胺之间结合得比较好。
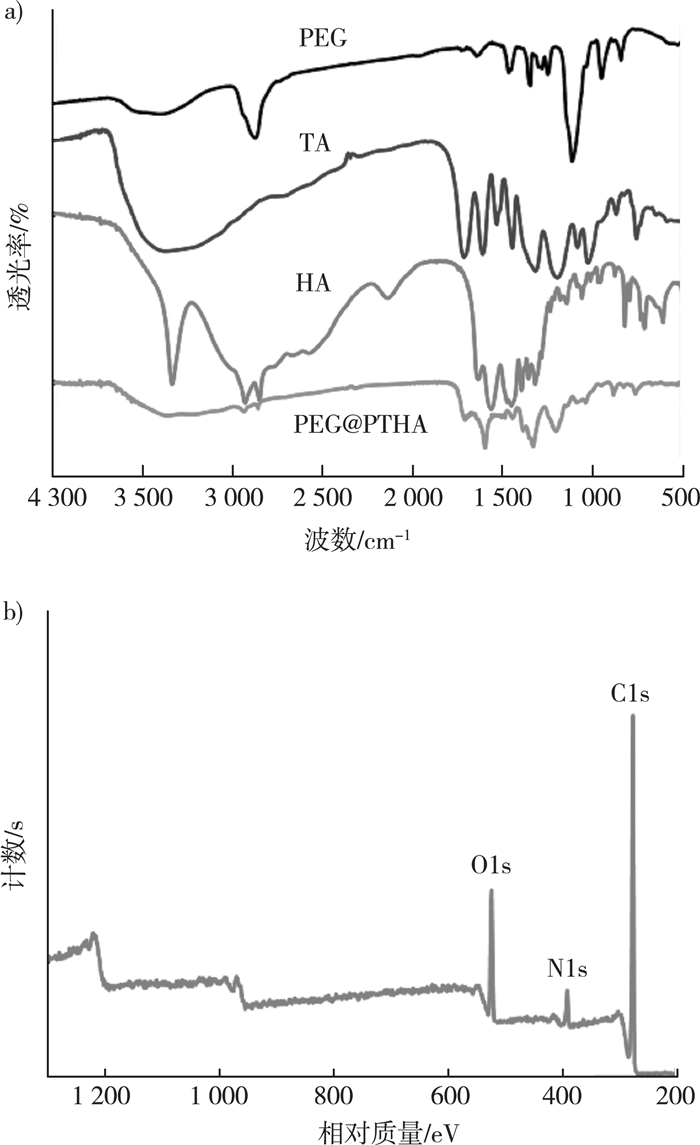 |
| 图 4 PEG@PTHA的FTIR (a)和XPS(b) |
图 4(b)为PEG@PTHA的XPS宽扫描图谱,可知C元素是构成PEG@PTHA的主要元素,O元素主要来源于单宁酸和聚乙二醇,N元素为己二胺所独有。上述结果表明,PEG@PTHA中有大量羟基、氨基等极性基团,而且不含其他元素组分,合成的PEG@PTHA是纯净的聚合物。
2.3 吸附结果 2.3.1 接触时间对吸附量的影响取20 mg吸附剂,放入盛有50 mL初始浓度为250 mg/L的CR溶液的锥形瓶中,于180 r/min转速、水浴温度303 K条件下,在0~48 h内不等时间隔取样离心处理。用紫外分光光度法(λ=497 nm)测其浓度,结果如图 5(a)所示。在开始的180 min内,吸附量随时间延长迅速增加,其后趋缓,12 h后基本不变。此时吸附量可达320 mg/g左右。吸附材料刚加入时表面有大量吸附位点,能迅速结合染料分子,随着吸附过程的继续进行,部分染料分子扩散进入材料内部,最后吸附剂逐渐饱和,吸附与脱附达到平衡。因此,吸附平衡时间为12 h左右。为使染料充分吸附,后续实验均将吸附时间设置为24 h。
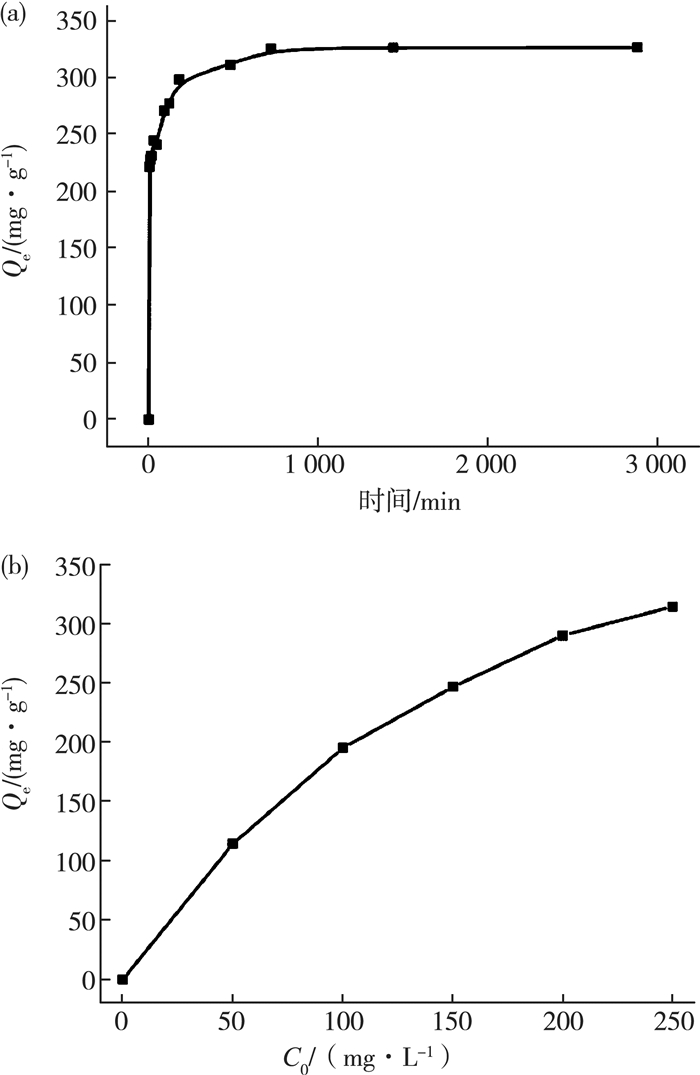 |
| 图 5 接触时间(a)和初始染料浓度(b) |
2.3.2 初始浓度对吸附量的影响
取20 mg吸附剂,分别放入盛有50 mL初始浓度不同(50~400 mg/L)的CR溶液中,于180 r/min转速、水浴温度为303 K条件下,震荡吸附24 h后取下,取样离心处理,用紫外分光光度法(λ=497 nm)测其浓度,结果如图 5(b)所示。在染料浓度较低时,吸附量随着初始浓度的增大而迅速升高。随着染料浓度的升高,吸附量增加趋缓,250 mg/L处吸附剂的吸附容量已趋于平衡,Qe达到最大值314.7 mg/g。继续增加浓度,吸附量不再发生明显变化。
2.3.3 吸附动力学溶液中的吸附是一个较复杂的过程。吸附质从液相中被吸附到吸附剂颗粒中,可以分为吸附剂周围流体界膜中吸附质的外迁移(外扩散)、吸附剂颗粒内扩散和吸附剂内的吸附反应等几个过程[7]。吸附过程的动力学研究主要是用来描述吸附剂从溶液中吸附溶质速率的快慢,通过动力学模型对数据的拟合,可以探究其可能的吸附机理。常用的动力学模型有准一级动力学方程、准二级动力学方程、颗粒内扩散模型等。
1) 准一级动力学方程
准一级动力学方程基于以下假设:在吸附过程中,吸附主要受扩散步骤(包括内扩散和外扩散)的影响,而吸附反应是一个迅速且阻力小的过程。则推导出的结论是:吸附速率与平衡吸附量(Qe)和t时刻吸附量(Qt)的差值成正比[10]。准一级动力学方程不适合描述整个吸附过程,但是对于反应的前20~30 min比较适合。其通用表达式为:
| $ {\rm{log}}({Q_e} - {Q_t}) = {\rm{log}}{Q_e} - {K_1}t/2.303 $ | (2) |
式中:K1为准一级动力学的速率常数,t为吸附时间(min)。以log(Qe-Qt)对t作图,可以通过斜率和截距分别求得K1和Qe。
2) 准二级动力学方程
准二级动力学方程认为:吸附过程中扩散步骤不是控制步骤,吸附反应中的化学吸附机理是控制整个吸附过程的决定因素,而此时吸附剂与吸附质之间化学作用含有电子对的转移、交换和共有过程[10]。其表达式为:
| $ t/{Q_t} = 1/\left( {{K_2}{Q_e}^2} \right) + t/{Q_e} $ | (3) |
式中:K2为准二级吸附动力学的速率常数。以t/Qt对t作图,可以通过斜率和截距求得Qe和K2的值。用以上两动力学模型对实验结果进行线性拟合,结果见图 6、表 2。
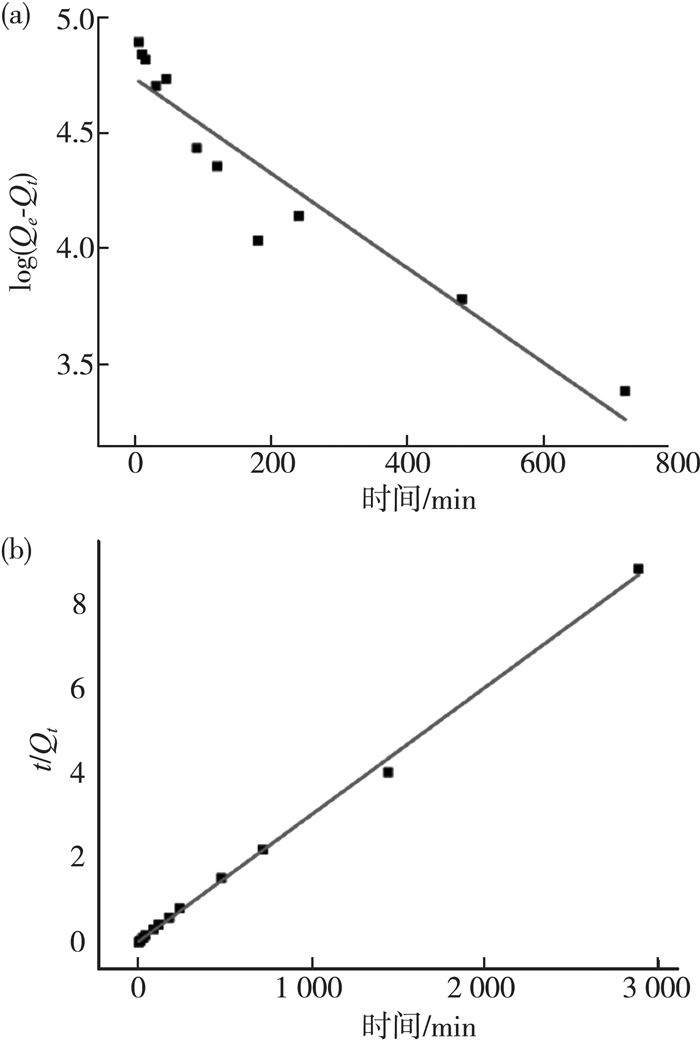 |
| 图 6 准一级动力学方程(a)和准二级动力学方程(b) |
| 表 2 PEG@PTHA对刚果红的吸附动力学方程参数 |
 |
拟合结果显示,通过准一级动力学方程拟合计算得到的Qe为114.14 mg/g,远小于实验值;而准二级动力学方程拟合得到的Qe为331.13 mg/g,与实验值非常接近。由表 2可知,准二级动力学方程拟合的R2 > 0.99,显然准二级动力学方程更适合用来描述微胶囊对刚果红的吸附过程。由此可初步判断该过程包含化学吸附,即吸附剂与吸附质之间形成了新的共价键。
3) 颗粒内扩散模型
颗粒内扩散模型假定颗粒内部扩散是速率控制步骤,适用于混合均匀的溶液。颗粒内部扩散模型是一个单一阻力模型,假设颗粒内部的扩散系数是个常数,且假设吸附剂吸附染料与溶液中染料的浓度相关度很小,这样可以从菲克定律中推测出。韦伯和莫里斯提出以下动力学模型,来研究吸附是颗粒内部扩散控制的[11]:
| $ {Q_t} = {K_{id}}{t^{1/2}} + C $ | (4) |
式中:Kid是颗粒内扩散速率常数,C是与边界层厚度常数。如果吸附过程符合颗粒内部扩散模型,则Qt与t1/2应该是线性关系。相反,若存在外部传质阻力和化学反应,直线并不通过原点。对于很多吸附过程,曲线通常是多线性的,通常可以将曲线分为两段或者更多的直线,然后对于每段直线赋予不同的控制机理[11]。
对于初始浓度为250 mg/L的刚果红的吸附速率曲线,用颗粒内扩散模型进行分析,如图 7所示。模拟出的曲线由三段直线组成,且并不通过原点,说明颗粒内扩散是速率控制的步骤,但不是唯一的控制步骤,吸附速率还受颗粒外扩散(比如液膜扩散、表面吸附等)控制。由结果可推测,第一阶段可能是以快速的物理吸附过程为主,因为吸附剂中含有大量酚羟基、氨基、亚氨基等极性基团,刚果红分子中也有极性的氨基基团,因此两者间会形成分子间的氢键以及存在范德华力等;第二阶段,随着分子内扩散的进行,可能以速率较慢的化学吸附为主;第三阶段则为吸附平衡阶段,此时吸附剂达到饱和。
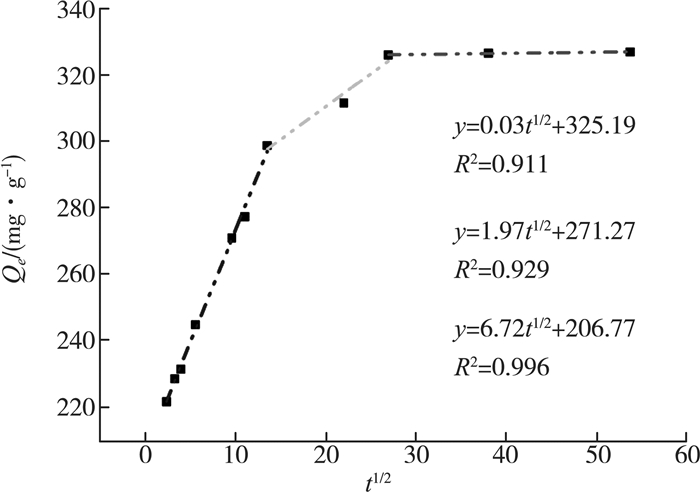 |
| 图 7 颗粒内扩散模型 |
2.3.4 吸附等温线
在环境温度保持不变的情况下,等温吸附线为吸附平衡时去除量与被吸附物浓度的关系曲线[12]。即通过改变吸附质浓度,吸附量会呈线性规律变化。Langmuir方程和Freundlich方程是应用最广的两个等温吸附模型。
1) Langmuir等温吸附模型
Langmuir方程基于以下假设:吸附剂具有均匀的表面,这样就规定了吸附质在吸附剂的任何吸附位点都具有相同的吸附能;吸附剂在吸附质表面是单分子层吸附,当吸附质完全覆盖吸附剂时,达到了吸附剂的饱和吸附量;一旦吸附质吸附在吸附剂表面,则在各吸附位点就不会出现吸附质的转移;达到平衡时,并不是静止过程,而是吸附和脱附的速率一样[10]。其表达式为[13]:
| $ {C_e}/{Q_e} + 1/\left( {{K_L}{Q_m}} \right) + {C_e}/{Q_m} $ | (5) |
式中:Ce为平衡时剩余溶液的离子浓度;Qe为处于平衡时的实际吸附量;KL为Langmuir模型的饱和吸附常数;Qm为饱和状态的最大去除量。如果吸附过程满足Langmuir等温吸附模型,通过拟合Ce/(Qe-Ce)可以得到一条直线,通过方程的斜率和截距的值进而计算出KL和Qm。采用无纲量的常数RL(分离因数)进一步分析Langmuir等温吸附模型。其表达式为[14]:
| $ {R_L} = 1/({K_L}{C_0} + 1) $ | (6) |
式中:C0是最高染料初始离子浓度(mg/L)。根据RL大小可以将等温吸附模型的吸附类型划分为四种:RL > 1,不利于吸附;0 < RL < 1,吸附是可以进行的;RL=1,吸附是线性的;RL=0,吸附是不可逆过程[15]。
2) Freundlich等温吸附方程
Freundlich方程基于以下假设:材料的功能基团分布不均匀,由不同类型的吸附位点组成,每一个活性位点的作用均可用Langmuir方程来模拟[16]。其线性表达方程为[17]:
| $ {\rm{log}}{Q_e} = {\rm{log}}{K_F} + 1/nlog{C_e} $ | (7) |
式中:Ce是吸附平衡时的溶液浓度;Qe是达到平衡时的实际吸附量;KF是吸附剂吸附能力的量度;n是吸附强度的量度。当n > 1时,属于优势吸附;当n=1时,是线性吸附;当n < 1时,是非优势吸附[18]。通过拟合后的直线的斜率和截距可以求得n和KF,拟合结果见图 8和表 3。
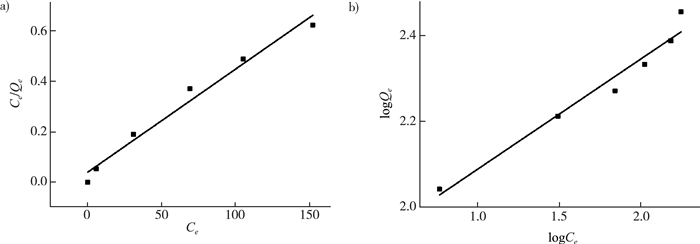 |
| 图 8 Langmuir吸附等温线和Freundlich吸附等温线 |
| 表 3 PEG@PTHA对刚果红的等温吸附方程参数 |
 |
可见,对刚果红的吸附过程较为满足Langmuir模型,其R2 > 0.966,理论吸附值为293.3 mg/g,与实际实验结果较为接近。而Freundlich模型中R2 > 0.899,因此微胶囊对刚果红的吸附过程更符合Langmuir方程。其表面性质较为均一,吸附过程为单分子层吸附。拟合得到的RL为0.002,因此吸附是可以进行的。由于Freundlich模型的n > 1,所以吸附过程为优势吸附。
3 结论1) 采用聚乙二醇、单宁酸、1, 6-己二胺合成了一种新的聚电解质复合物微胶囊PEG@PTHA,用TEM、FTIR、XPS对材料进行了表征。结果显示合成的PEG@PTHA球形完整,表面较粗糙,平均粒径约为200 nm,有明显的核-壳结构;PEG@PTHA含有大量极性基团,可以较好地吸附染料分子。
2) PEG@PTHA可以有效地吸附刚果红。实验结果表明:水浴温度为303 K时,吸附过程在12 h内达到平衡,理论计算最大Qm为293.3 mg/g。吸附量随染料初始浓度的增加而增加,在实验条件下染料浓度为250 mg/L时最大吸附量为314.7 mg/g。
3) 吸附剂对CR的吸附行为符合准二级动力学方程。颗粒内扩散是速率控制的步骤,但不是唯一的控制步骤,吸附速率还受颗粒外扩散控制。吸附等温线可用Langmuir等温吸附模型来较好地描述,吸附过程可能同时包含化学吸附和物理吸附作用。
| [1] |
DIZGE N, AYDINER C, DEMIRBAS E, et al. Adsorption of reactive dyes from aqueous solutions by fly ash:Kinetic and equilibrium studies[J]. Journal of Hazardous Materials, 2008, 150(3): 737-746. DOI:10.1016/j.jhazmat.2007.05.027 |
| [2] |
ALJEBOREE A M, ALSHIRIFI A N, ALKAIM A F. Kinetics and equilibrium study for the adsorption of textile dyes on coconut shell activated carbon[J]. Arabian Journal of Chemistry, 2017, 10: S3381-S3393. DOI:10.1016/j.arabjc.2014.01.020 |
| [3] |
MIANDAD R, KUMAR R, BARAKAT M A, et al. Untapped conversion of plastic waste char into carbon-metal LDOs for the adsorption of Congo red[J]. Journal of Colloid and Interface Science, 2018, 511: 402-410. DOI:10.1016/j.jcis.2017.10.029 |
| [4] |
SHABAN M, SAYED M I, SHAHIEN M G, et al. Adsorption behavior of inorganic-and organic-modified kaolinite for Congo red dye from water, kinetic modeling, and equilibrium studies[J]. Journal of Sol-Gel Science and Technology, 2018, 87: 427-441. DOI:10.1007/s10971-018-4719-6 |
| [5] |
刘强.酚基螯合树脂及其复合材料制备与吸附性能研究[D].济南: 齐鲁工业大学, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10431-1018058148.htm
|
| [6] |
ABDELKADER M B, AZIZI N, BAFFOUN A, et al. New microcapsules based on isosorbide for cosmetotextile:Preparation and characterization[J]. Industrial Crops & Products, 2018, 123: 591-599. |
| [7] |
HITCHCOCK J, TASKER A L, STARK K, et al. Adsorption of catalytic nanoparticles onto polymer substrates for controlled deposition of microcapsule metal shells[J]. Langmuir, 2018, 34: 1473-1480. DOI:10.1021/acs.langmuir.7b02874 |
| [8] |
姜涛, 胡亚楠, 龙玥, 等. 刺激响应型微胶囊的可控释放研究进展[J]. 影像科学与光化学, 2015, 33(2): 1-2. |
| [9] |
LI Z, CHEN J, GE Y. Removal of lead ion and oil droplet from aqueous solution by lignin-grafted carbon nanotubes[J]. Chemical Engineering Journal, 2017, 308: 809-817. DOI:10.1016/j.cej.2016.09.126 |
| [10] |
SHABAN M, ABUKHADRA M R, SHAHIEN M G, et al. Upgraded modified forms of bituminous coal for the removal of safranin-T dye from aqueous solution[J]. Environmental Science and Pollution Research, 2017, 24: 18135-18151. DOI:10.1007/s11356-017-9424-4 |
| [11] |
HADDADE M, REGTI A, SLIMANI R, et al. Assessment of the biosorption kinetic and the modynamic for the removal of safranin dye from aqueous solutions using calcined mussel shell[J]. Journal of Industrial and Engineering Chemistry, 2014, 20(2): 717-724. DOI:10.1016/j.jiec.2013.05.038 |
| [12] |
SELIEM M K, KOMARNENI S, ABUKHADRA M R. Phosphate removal from solution by composite of MCM-41 silica with rice husk:kinetic and equilibrium studies[J]. Microporous and Mesoporous Materials, 2016, 224: 51-57. DOI:10.1016/j.micromeso.2015.11.011 |
| [13] |
WAN H, WANG B, LI J, ZHU T. Adsorption equilibrium and thermodynamics of acetaldehyde/acetone on acti-vated carbon[J]. Separation and Purification Technology, 2018, 209: 535-541. |
| [14] |
LEI C, PI M, JIANG C, et al. Synthesis of hierarchical porous zinc oxide (ZnO) microspheres with highly efficient adsorption of Congo red[J]. Journal of Colloid and Interface Science, 2017, 490: 242-251. DOI:10.1016/j.jcis.2016.11.049 |
| [15] |
FARNAD N, FARHADI K, VOELCKER N H. Polydopamine nanoparticles as a new and highly selective biosorbent for the removal of copper (Ⅱ) ions from aqueous solutions[J]. Water, Air, & Soil Pollution, 2012, 223(6): 3535-3544. |
| [16] |
HATCH C D, WIESE J S, Crane C C, et al. Water adsorption on clay minerals as a function of relative humidity:application of BET and Freundlich adsorption models[J]. Langmuir, 2012, 28(3): 1790-1803. DOI:10.1021/la2042873 |
| [17] |
HABIBA U, SIDDIQUE T A, JOO T C, et al. Synthesis of chitosan/polyvinyl alcohol/zeolite composite for removal of methyl orange, Congo red and chromium (Ⅵ) by flocculation/adsorption[J]. Carbohydrate Polymers, 2017, 157: 1568-1576. DOI:10.1016/j.carbpol.2016.11.037 |
| [18] |
TSENG R L, WU F C. Inferring the favorable adsorption level and the concurrent multi-stage process with the Freundlich constant[J]. Journal of Hazardous Materials, 2008, 155(1): 277-287. |
 2019, Vol. 33
2019, Vol. 33


