| 声音检测与分贝转化的仿真与设计 |
b. 江南大学人工智能与计算机学院, 江苏 无锡 214122
b. School of Artificial Intelligence and Computer Science, Jiangnan University, Wuxi 214122, China
声音是生活中普遍存在的一种自然现象, 声音的检测与分析是人类研究自然与环境本质的一种科学方式[1-2]。通过检测结果的多样性和规律性可以去获得更多的有效信息, 被广泛应用于医疗卫生[3-4]、铁路工程[5]、环境检测[6]、农业生产等多领域[7]。
其中声音的分贝检测应用较为广泛, 其重点在于声音的采集与有效值转换。在上世纪80年代, 交流信号有效值通常采用通用晶体管测量, 但是数值并不准确, 测量的仅仅是整流平均值。到了二十世纪末, 三值电压表逐渐被使用, 能够测量波顶因数有限的波形有效值, 其中最常用的属于折线逼近抛物线法, 但测量精度都有待提高。近些年来, 随着集成电路的发展, 一些基于热等效法和定义法的测量芯片不断出现, 将精度和适用范围进一步提高, 但是价格都十分昂贵, 用在声音检测方面性价比不高。
本文设计了一款声音分贝检测电路, 在人耳可听的频率范围内, 仿真测试该电路对于不同声压级、不同频率信号的适应能力。对于不同的声压级采取不同的放大倍数, 有效地将声音信号转化为真有效值, 进一步转化为分贝输出。在前置放大器方面, 采用跨阻放大器放大微弱的声音信号, 同时抑制噪声。在分贝数值转化方面采用隐式有效值法和快速傅里叶变换法, 通过软硬件对比, 其中硬件电路结构相对复杂但是能够有效测量频率的数值, 软件设计的实时性更高, 需要采取设置合适的采样频率等方法来防止频谱泄露, 从而实现结果的准确性[8]。相比于市面上的集成芯片AD637, 该电路成本低廉, 在人耳可听频率范围内精度较高。此外, AD637测量真有效值的上限是2 V, 本文设计电路可以测量最高达3 V的真有效值, 可行性较强。
1 方案设计本文电路主要由前置放大器、带通滤波电路、后级放大电路以及有效值运算电路组成。其中声音信号的采集与滤波电路是公共部分, 后级放大电路根据声压级的大小分为3个部分, 有效值的计算采取两种方式, 根据搭配的主控芯片选择适当方式进行计算。此外, 可以采取添加频率计电路来实现测频功能[9]。
1.1 前置放大电路前置放大器电路选用GMI4015P-2C全指向驻极体咪头, 驻极体咪头主要由电阻电容以及结型场效应管组成, 特点是体积较小、频率响应特性好, 适用于声音的采集[10]。
咪头的输出信号通常比较小, 通过跨阻放大器, 将输出电流转化为电压信号。前置放大器的原理图如图 1所示。
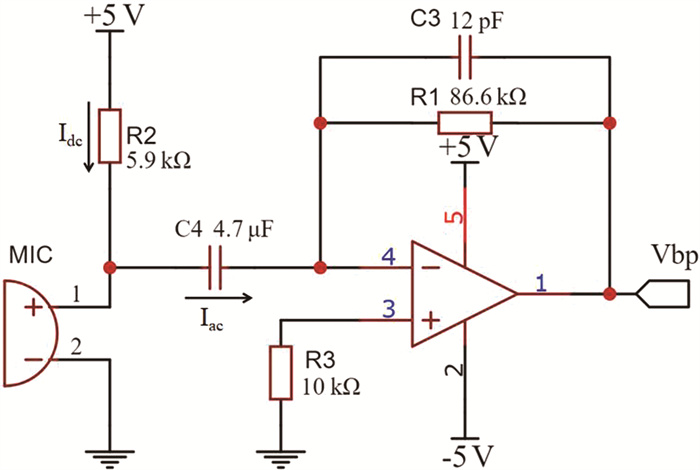 |
| 图 1 咪头前置放大器电路 |
R2是咪头中场效应管的漏极偏置电阻, Idc是电路中存在的直流分量, 同时声波引起的交流分量用Iac表示。后级滤波器的输入电压用Vbp表示, 在转折频率范围内公式表达为:
| $ V_{\mathrm{bp}}=I_{\mathrm{ac}} \times R_{1} 。$ | (1) |
咪头的灵敏度是指在输入端施加1 Pa的声压时, 输出端产生的电压大小, 单位用dBV表示, 而模拟量可以用mV/Pa来表示, 转化的公式为:
| $ S_{\mathrm{dBV}}=20 \times \log _{10}\left(\frac{S_{\mathrm{mV} / \mathrm{Pa}}}{O_{\mathrm{REF}}}\right) 。$ | (2) |
本文选用的咪头灵敏度SdBV为-48 dB, 参考基准OREF为1 V/Pa, 将参数带入得到模拟量表示的灵敏度为3.981 mV/Pa。考虑到咪头的输出阻抗为2.2 kΩ, 设定采集的最大声压级为100 dB, 对应的声压大小为2 Pa, 放大后的输出电压设置为0.316 Vrms, 达到传统音频接口的标准, 则咪头产生的输出电流为3.619 μA。
由于采用的是跨阻抗放大器, 所以电路的增益为:
| $ R_{1}=\frac{V_{\mathrm{bp}}}{I_{\mathrm{out}}}{ } 。$ | (3) |
增益计算结果为87.3, 这里R1选取标称值为86.6 kΩ。反馈电容C3的取值根据公式求得为13.7 pF:
| $ C_{3}=\frac{1}{2 \pi f_{p} R_{1}} 。$ | (4) |
这里的fP指的是在20 kHz, 响应误差为0.1 dB的极点位置, C3选用NPO或者C0G等Ⅰ类陶瓷电容, 失真影响小且稳定性更高, 选用标称值12 pF。
电阻R2的取值由供电电压以及咪头最大消耗电流和工作电压决定, 在设计时留有一定裕量, 用来适应电源电压的微小变化。增大R2的取值可以降低整体的噪声增益, R2和C4构成了高通滤波器。这个电路的增益完全由R1决定, 而噪声增益却是由R1、R2共同决定, 同时C4在声波频率范围内具有较低的阻抗, 使得场效应管的漏极电压变化特别小, 从而降低沟道长度调制效应带来的影响。
1.2 滤波及后级放大电路信号经过前置放大器以后, 经过滤波器去除杂波, 同时可以通过修改电阻电容的取值实现相应的计权方式, 本文设置的范围是20 Hz到20 kHz, 对该范围内信号没有进行衰减。整体电路如图 2所示。此外, 也可以采用数字滤波器来实现频率计权。
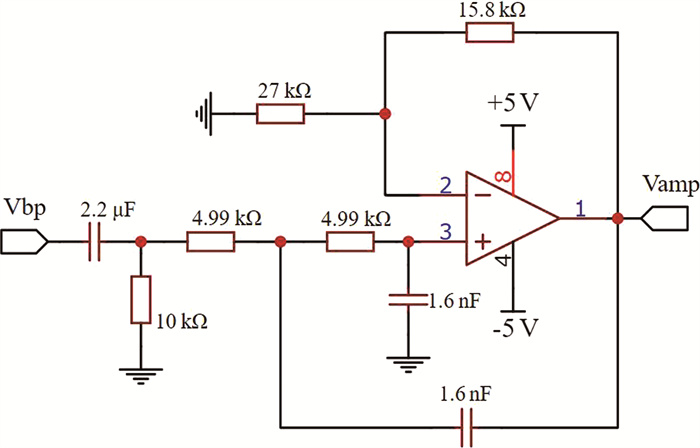 |
| 图 2 滤波电路 |
滤波后根据不同的声压级采取衰减或放大, 共分为3段电路, 使得后续的均方根电路的输入信号一直处于合理范围内。输出的信号经过转化, 传递给主控芯片处理。此外, 在每一级电路之间都要添加合适的RC滤波电路来有效地去除直流信号, 尤其是要去除经过反向放大产生的负电压。
1.3 均方根计算电路交流信号的有效值计算方法有很多, 其中热等效法测量最为精准但是不适合快速测量, 传统的峰值检测法和平均值法仅适用于正弦波[11-12]。本文采取的是真有效值法以及交流采样法, 通过软硬件结合的方式, 来测量声音信号的有效电压值, 进一步转化为分贝值, 适用于任意波形。
真有效值法是用全波整流的方式求得交流信号的绝对值, 再通过对数指数电路运算, 得到最终的有效值, 它的最初定义是均方根法, 严格按照数学概念的推导得到周期信号的有效值是它的实时连续采样值进行均方根的计算[13]。用积分的表达形式为:
| $ V_{\mathrm{rms}}=\sqrt{\frac{1}{T} \int_{0}^{T} u(t)^{2} \mathrm{~d} t} \approx \sqrt{\overline{u^{2}}} 。$ | (5) |
考虑到人耳能听到的极限声音的频率为20 Hz到20 kHz, 带宽并不大, 于是采取隐式计算法, 通过对数-指数电路的变化, 在牺牲带宽的情况下扩大了输入的动态范围, 信号呈线性关系, 成本也更低。对定义公式进行恒等变换, 得到变化式为:
| $ V_{\mathrm{rms}}=\mathrm{e}^{\left(2 \ln V_{\mathrm{i}}-\ln V_{\mathrm{rms}}\right)} 。$ | (6) |
绝对值电路是将信号转化到对数运算的输入范围内, 采用两个单电源运放来实现, 避免了传统整流二极管对电路产生的影响[14]。对数-指数运算电路采取运放、三极管与二极管等元件构成, 整体电路图如图 3所示:
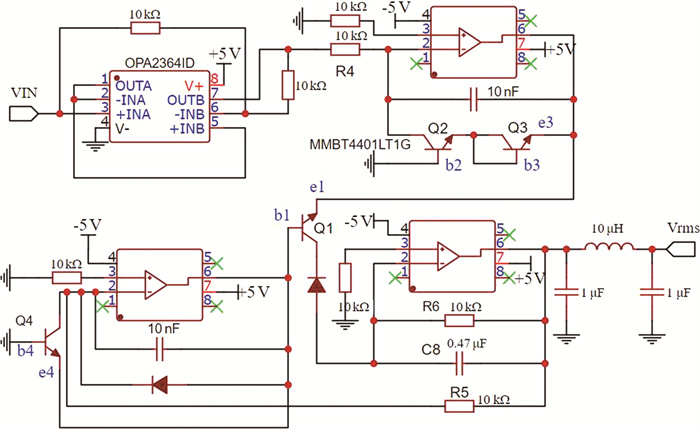 |
| 图 3 有效值运算电路 |
三极管Q2、Q3与运放构成输入信号的对数电路, 根据PN结的特性, 输出端电位分析:
| $ V_{e 1}=V_{\mathrm{e} 3} \approx-2 U_{T} \ln \frac{V_{i}}{I_{S} R_{4}}, $ | (7) |
其中UT是温度电压当量, IS是反向饱和电流。
Q4与运放构成输出信号的反馈对数电路, 在Q1处的电位同理可得:
| $ V_{\mathrm{b1}}=V_{\mathrm{e4}} \approx-U_{T} \ln \frac{V_{\mathrm{rms}}}{I_{S} R_{5}}, $ | (8) |
于是计算指数电路的输出端电压为:
| $ V_{\mathrm{rms}}=-I_{R_{6}} \times R_{6}=-I_{S} \mathrm{e} \frac{V_{b 1}-V_{e 1}}{U_{T}} \times R_{6}, $ | (9) |
将Vb1和Ve1的公式代入, 得到最终表达式为:
| $ V_{\mathrm{rms}}=\sqrt{{\frac{R_{5} R_{6}}{R_{4}{ }^{2} }}V_{i}{ }^{2}}=\sqrt{V_{i}^{2}} 。$ | (10) |
交流采样法是利用主控芯片对输入的交流信号进行快速采样, 实时性强且采样频率可以根据实际情况不断调整, 同时省去了复杂的电路设计[15]。电路采集时需要添加直流偏置, 交流信号直接传递给主控芯片, 通过快速傅里叶变换求得声波信号中的基波以及其他谐波的幅值, 进一步求得叠加的交流信号的幅值与有效值。
2 电路仿真与软件测试本文的电路优势在于成本低廉的同时测量精准, 性价比很高。传统的峰值检测等方法, 并不适用于混合波形, 且误差较大[14]。而最近热门的集成芯片, 例如AD637, 最低售价都要几十元甚至上百元, 与本文设计的电路方案对比成本太高, 同时在人耳可听频率范围内使用时, 两者的精度差别微乎其微。此外, 本文设计的电路最多可以测量有效值高达3 V的交流信号, 远远高于AD637芯片2 V的输入上限。在测量微弱信号时, AD637的反应时间是以s为单位, 远远大于本文设计电路的反应时间。将传统的平均值法测量与本文设计电路进行对比, 实验结果表明本文设计电路将精度提高了3%左右, 误差小且成本较低。
2.1 输入声压范围测试本文设计的最大输入声压级为100 dB。这里以70 dB声压级, 20 kHz输入信号来举例, 如图 4所示:
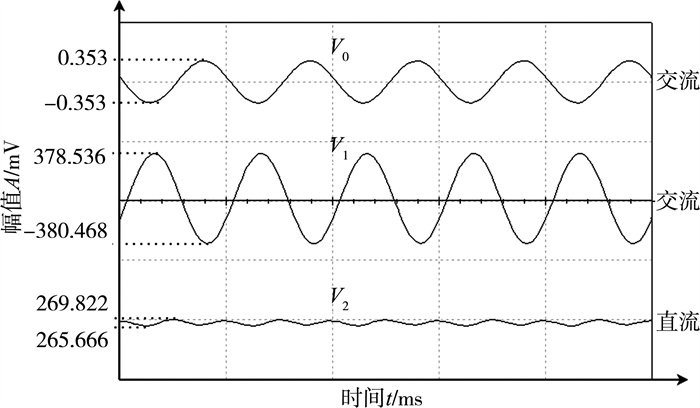 |
| 图 4 3种波形信号 |
其中V0是咪头产生的输入交流信号, V1是经过放大滤波后的交流信号, V2是经过有效值电路后转化的直流信号。
考虑到有效值电路的输入信号小于60 mV时误差波动比较大, 因此根据不同的声压级输入采取不同的放大倍数, 当输入声压小于55 dB时, 采取二级放大; 处于55 dB到75 dB时采取一级放大; 当信号高于75 dB时, 前置放大直接输出。测量输入信号频率为20 kHz, 声压级大小为40到85 dB时的电路参数, 如表 1所示。
| 表 1 不同声压级的信号参数 |
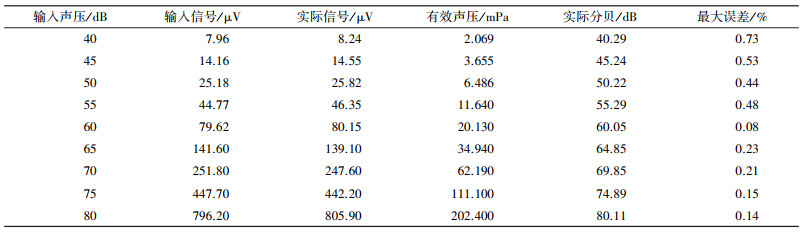 |
其中输入信号是指对应声压级情况下, 咪头产生的电压大小。实际信号是输出信号除以放大倍数以后的真实数值。有效声压是实际信号除以咪头灵敏度得到的数值。实际分贝是按照分贝计算公式求得的:
| $ L_{P}=20 \times \log _{10} \frac{P}{P_{\mathrm{ref}}}, $ | (11) |
其中, P是测量的有效声压值; Pref是空气中参考声压的有效值, 一般取值为20 μPa。
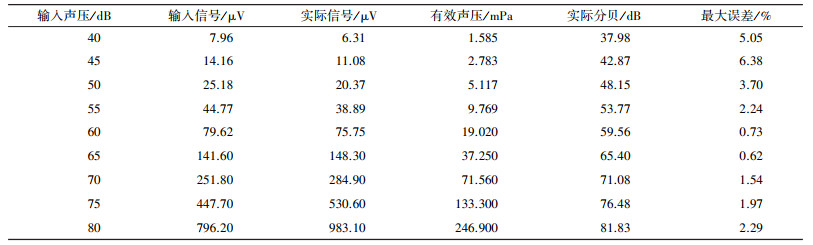
从表 1中可以看到整体的平均误差在0.3%左右, 选择合适的放大倍数后在较宽的声压级输入范围内转化的结果都较为精准。该设计适合测量整体的环境分贝大小。同时在同等条件下测量平均值法的信号参数, 数据如表 2所示, 可以明显看到最大误差的平均值大约在3%, 远远大于本文设计电路。
| 表 2 平均值电路的不同声压信号参数 |
 |
2.2 输入频率范围测试
人耳能听到的极限频率范围为20 Hz到20 kHz之间, 而市面上通用的咪头采集频率一般是100 Hz到10 kHz。这里设定声压级大小固定为70 dB, 测试50 Hz到15 kHz的信号参数, 如表 3所示。
| 表 3 不同频率下的信号参数 |
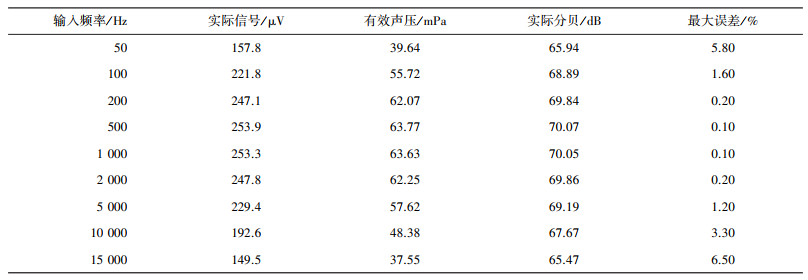 |
从表 3中可以看出, 不同的频率范围电路的适应能力差距明显, 平均误差在2.5%左右。本文设计的电路主要针对人耳敏感的频率范围500到5 000 Hz, 误差在大约0.3%, 对于其他频率的输入信号精度有所下降, 可以通过更改电路中C8的容值大小来实现对应频率范围内的精确测量。
平均值电路对放大微弱信号的精确度很低, 但测量放大后的信号实际误差比较小, 这里选取最精准的放大信号来作为参考, 在同等条件下测试平均值法电路, 同时对数据进行再平均处理, 数据参数如表 4所示:
| 表 4 平均值电路的不同频率信号参数 |
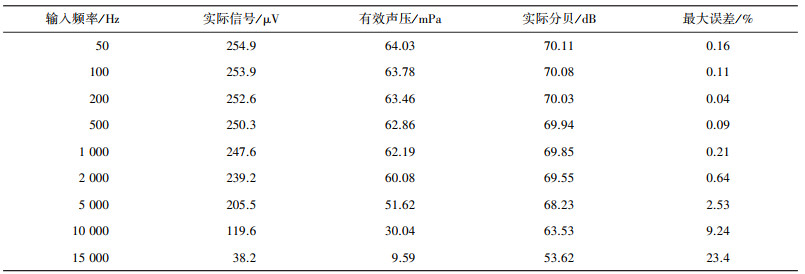 |
从表 4中很明显可以看出, 仅仅在2 000 Hz以下时, 平均值电路有较好精度。整体电路对输入信号范围有严格的要求, 且采集数据需要后续芯片进行再一步处理。平均值电路针对人耳敏感频率误差在1%, 且全频率范围整体误差在4%左右, 精度远低于本文设计电路。
2.3 输入叠加波形测试考虑到生活中不会存在稳定单一的声音信号, 大多是各种信号叠加输出, 于是通过软件搭建一个由四个波形叠加而成的输入信号, 观察它最终的结果与实际的误差大小[13]。信号的表达式为:
| $ V_{i}=0.3 \sqrt{2} \sin (200 \pi t)+0.6 \sqrt{2} \sin (1000 \pi t+30)+0.7 \sqrt{2} \sin (2500 \pi t+45)+\sqrt{2} \sin (4000 \pi t+60) 。$ | (12) |
通过示波器观察输入以及输出信号的波形, 如图 5所示。此时只采取了前置放大, 将输出信号除以放大系数, 得到有效值在1.304到1.478 V之间波动, 求平均得1.391 V与理论值1.393 V基本保持一致。传统测量方法并不能测得混合波形的有效值, 这是本设计相比于平均值电路的优势所在。
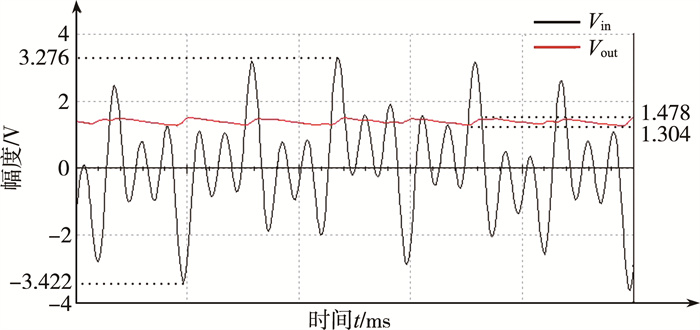 |
| 图 5 输入与输出信号波形 |
2.4 交流采样法测试
交流采样则通过Matlab建立信号的输入, 当采样频率为5 kHz和4 096 Hz时, 得到的频域图分别如图 6、图 7所示。当采样频率为5 kHz时, 结果并没有提升, 反而在500和2 000 Hz处发生了频谱泄露。当使用快速傅里叶变换时, 采样频率需要为被测频率的2的N次方, 此时采样的精度是最为准确的。最终结果为1.389 V, 在设置时可以通过添加适当的窗函数来滤波, 或者采用软件同步、添加补偿因子、修正采样序列等方法进一步提高整个采样的准确性[16-17]。交流采样法适用于处理能力强的主控芯片, 优点在于采样频率可以随时更改, 同时可以得到所有信号的输入频率与分贝大小, 适用于测量多频率分贝。
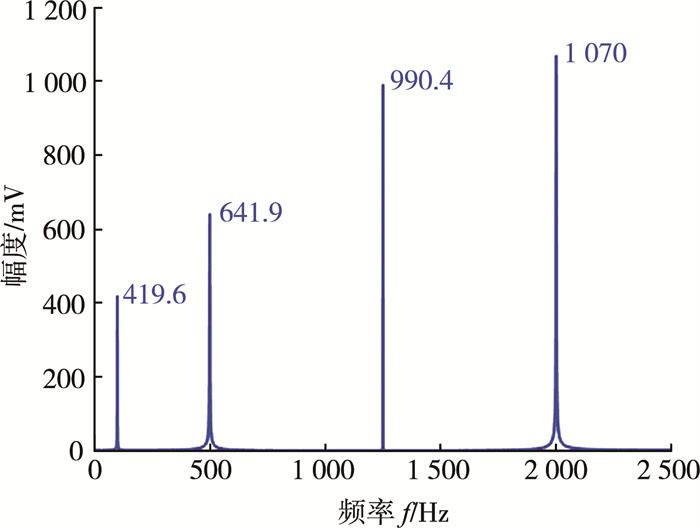 |
| 图 6 采样频率为5 kHz时的频域图 |
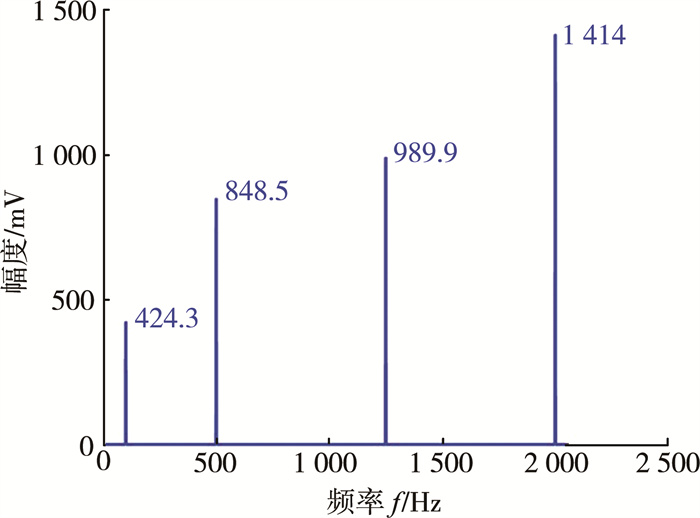 |
| 图 7 采样频率为4 096 Hz时的频域图 |
3 硬件实物图
实际测量的部分电路如图 8所示。
 |
| 图 8 实物测量图 |
4 结束语
本文搭建了一个声音采集及分贝转化电路, 并仿真测试了该电路对于不同声压级、不同频率信号的适应能力。对于不同的声压级采取不同的放大倍数, 测量结果表示整体设计的精确度较高, 可以实现人耳可听范围内的声音测量及分贝转化。
其中有效值法适用于测量环境分贝, 对主控芯片要求较低。而交流采样法可以测量多频率不同信号分贝, 适用于处理能力强的芯片, 同时需要正确设置采样频率。此外, 使用傅里叶变换有利于后续采用深度学习理论, 通过神经网络对声音信号进行进一步识别与分类[18]。
| [1] |
薛英杰, 韩威, 周松斌, 等. 基于生成对抗单分类网络的异常声音检测[J]. 吉林大学学报(理学版), 2021, 59(6): 1517-1524. DOI:10.13413/j.cnki.jdxblxb.2021067 |
| [2] |
马庆禄, 邹政, 刘丰杰. 基于行车声音端点检测的交通量统计[J]. 科学技术与工程, 2020, 20(4): 1676-1683. DOI:10.3969/j.issn.1671-1815.2020.04.058 |
| [3] |
程珊珊, 石波, 曹阳. 心电信号采集技术研究进展[J]. 齐鲁工业大学学报(自然科学版), 2014, 28(4): 75-79. DOI:10.16442/j.cnki.qlgydxxb.2014.04.015 |
| [4] |
本刊讯. 便携式AI设备将咳嗽声音转化为健康数据以进行流感和流行病预测[J]. 数据分析与知识发现, 2020, 4(4): 43. |
| [5] |
高磊, 刘振奎, 魏晓悦, 等. 铁路隧道二次衬砌敲击检查声音特征分析及智能识别[J/OL]. 铁道科学与工程学报: 1-10. [2022-01-11]. DOI: 10.19713/j.cnki.43-1423/u.T20210807
|
| [6] |
张剑锋, 范雄方, 杨辉, 等. 基于STM32的内河船舶舱内环境在线监测系统设计[J]. 四川轻化工大学学报(自然科学版), 2021, 34(2): 51-59. |
| [7] |
廖正睿, 阳娜, 朱晓彤, 等. 声音干预对育肥猪采食行为和生产性能的影响[J/OL]. 江西农业大学学报: 1-11[2022-01-11]. http://kns.cnki.net/kcms/detail/36.1028.S.20211231.1715.006.html.
|
| [8] |
於玺. 快速傅里叶变换在信号处理中的应用[J]. 信息记录材料, 2021, 22(10): 184-186. |
| [9] |
郑太恒, 孙凤乾, 刘海英, 等. 智能频率计的研究与设计[J]. 齐鲁工业大学学报, 2021, 35(2): 56-61. DOI:10.16442/j.cnki.qlgydxxb.2021.02.009 |
| [10] |
BUSCH-VISHNIAC I J, ELKO W. Nearly 40 years of domination by electret microphones[J]. The Journal of the Acoustical Society of America, 2021, 149(4): 7-8. DOI:10.1121/10.0003934 |
| [11] |
王尧君, 刘冲, 蒋慧. 两种测量电压有效值方法的比较[J]. 中国测试, 2013, 39(3): 27-30. |
| [12] |
王小霞, 陈练, 李心耀. 任意高频信号真有效值测量技术[J]. 信息与电子工程, 2010, 8(5): 569-572. DOI:10.3969/j.issn.1672-2892.2010.05.015 |
| [13] |
谢然, 高常进, 窦永磊, 等. 戴光宇. 基于真有效值法测量交流电压信号有效值的仿真研究[J]. 中国特种设备安全, 2018, 34(7): 7-11. DOI:10.3969/j.issn.1673-257X.2018.07.002 |
| [14] |
陈仁伟, 朱长青, 岳夕彪. 高准确度有效值转换电路的设计与实现[J]. 电子测量技术, 2010, 33(6): 20-22, 26. DOI:10.19651/j.cnki.emt.2010.06.006 |
| [15] |
李庆波, 王菽蓉, 徐勇. 采样计算式测量方法的特点及应用[J]. 电测与仪表, 1999(9): 4-6. |
| [16] |
颜小君, 刘觉民, 陈明照, 等. 一种改进的软件同步交流采样法[J]. 仪表技术, 2007(4): 10-11. DOI:10.19432/j.cnki.issn1006-2394.2007.04.003 |
| [17] |
剧晶晶, 韩国政, 郑加健. 一种基于修正采样序列的傅里叶测频算法[J]. 齐鲁工业大学学报, 2020, 34(6): 44-49. DOI:10.16442/j.cnki.qlgydxxb.2020.06.007 |
| [18] |
乔风娟, 郭红利, 李伟, 等. 基于SVM的深度学习分类研究综述[J]. 齐鲁工业大学学报, 2018, 32(5): 39-44. DOI:10.16442/j.cnki.qlgydxxb.2018.05.008 |
 2022, Vol. 36
2022, Vol. 36

