| 基于UDE的复杂扰动下机械臂轨迹精确跟踪控制 |
机械臂作为机器人系统的一个重要分支, 是21世纪应用最广泛的工业产品之一[1]。当前, 机械臂越来越多的应用在远程手术、航空航天、高精密产品装配等方面, 因此, 对于机械臂的高精度的轨迹跟踪控制是必不可少的, 国内外学者们聚焦于此。但是, 机械臂是一个多自由度的非线性系统, 由于复杂的工作环境对其产生的干扰影响, 如风速、粉尘、噪声等等, 使得机械臂精确控制成为学者们的研究难点和热点。如何设计一个处理非线性和扰动的控制器, 国内外许多学者提出了新的控制方法, 例如, 鲁棒控制[2]、模糊控制[3]、神经网络控制[4], 不确定性和扰动估计(UDE)控制[5]等。
文献[6]提出了一种基于神经网络的控制策略, 控制具有学习能力、容错能力和鲁棒性, 在机械臂跟踪控制中应用较多, 缺点是需要大量的训练和样本。文献[7]提出了有限时间滑模控制, 通过了收敛速度, 但是在实际应用中机械臂会产生高频抖动的问题, 会加剧机械元件磨损, 导致系统控制效果降低, 甚至失去控制。文献[8]提出了一种自适应轨迹跟踪控制方法, 但该方法移植性差, 工程实现难度较大。到目前为止, UDE控制方法已经在非线性系统中取得了很好的理论成果[9-10]。然而, 传统的UDE控制的缺点是使用低通滤波器[11]只能处理有界的不确定性和扰动。而新的UDE控制器可以处理无界的外部扰动, 保证系统的渐近稳定。因此, 尽管系统存在干扰, 机械臂仍可以在整个控制过程中跟踪理想轨迹。由上述可知, 目前含有无界外部扰动的机械臂跟踪控制研究还是比较少的, 且控制器复杂, 不容易实现。
UDE控制是一种通过设计滤波器进行估计不确定性和扰动来实现控制效果的策略[12-13], 具有较好的鲁棒性, 且可以处理外部扰动, 控制器设计简单, 效果明显。目前在实际应用中, 无界的外部扰动也是真实存在的[14]。为了研究机械臂轨迹精确跟踪控制问题, 本文针对二自由度机械臂轨迹精确跟踪控制的问题, 对于系统存在无界外部扰动, 设计了反馈线性化控制器和UDE控制相结合的轨迹跟踪方法, 并进行仿真验证了机械臂轨迹跟踪的准确性和有效性。
1 模型建立与预备知识 1.1 机械臂动力学模型两关节机械臂如图 1所示, 其系统的动力学模型可表示为:
| $ \boldsymbol{D}(q) \ddot{q}+\boldsymbol{C}(q, \dot{q})+\boldsymbol{G}(q)=f, $ | (1) |
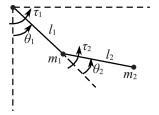 |
| 图 1 两关节机械臂 |
其中, q,
| $ \boldsymbol{D}(q)=\left[\begin{array}{ll} m_1 l_1^2+m_2\left(l_1^2+l_2^2+2 l_1 l_2 \cos q_2\right) & m_2\left(l_2^2+l_1 l_2 \cos q_2\right) \\ m_2\left(l_2^2+l_1 l_2 \cos q_2\right) & m_2 l_2^2 \end{array}\right], $ | (2) |
| $ \boldsymbol{C}(q, \dot{q})=\left[\begin{array}{c} -m_2 l_1 l_2 \sin q_2 \dot{q}_2\left(2 \dot{q}_1+\dot{q}_2\right) \\ m_2 l_1 l_2 \dot{q}_1^2 \sin q_2 \end{array}\right], $ | (3) |
| $ \boldsymbol{G}(q)=\left[\begin{array}{c} \left(m_1+m_2\right) g l_1 \sin q_1+m_2 g l_2 \sin \left(q_1+q_2\right) \\ m_2 g l_2 \sin \left(q_1+q_2\right) \end{array}\right], $ | (4) |
其中, m1和m2分别为连杆的质量;l1和l2分别是两个连杆的长度;g表示重力加速度。然而, 由于机械臂在工作中会受到周围环境等因素的影响, 所以外部扰动对于机械臂运动的干扰是不可避免的。因此, 机械臂动力学模型可以重新表示为:
| $ \ddot{q}=\boldsymbol{D}^{-1}(q)[f-\boldsymbol{C}(q, \dot{q})-\boldsymbol{G}(q)]+d, $ | (5) |
其中, d表示无界的外部扰动。
我们的目标是设计一个控制器, 使机械臂各关节跟踪给定的目标路径。
1.2 UDE控制方法UDE控制器主要用于处理模型不确定性和外部干扰。该方法的基本思想是通过设计合适的滤波器来估计模型不确定性和外部干扰。考虑如下的受控非线性系统:
| $ {\dot x}=f(x)+\mathit{\boldsymbol{b}} u+d^{\prime} \text {, } $ | (6) |
其中, x∈Rn是状态变量, u=us+uude;us为跟踪控制器;uude表示不确定性和扰动估计控制器;b∈Rn×r是一个常数矩阵;r≥1, d′表示有界的外部扰动。
引理1:对于系统(6), 如果设计的滤波器yf(t)满足以下条件:
| $ \tilde{d}=\hat{d}-d^{\prime}=0, t \rightarrow \infty, $ | (7) |
其中,
| $ u_{\mathrm{ude}}=b^{+}\left\{\ell^{-1}\left[\frac{\varphi_f(s)}{1-\varphi_f(s)}\right] *\left(f(x)+u_s\right)\right\}-b^{+}\left\{\ell^{-1}\left[\frac{s \varphi_f(s)}{1-\varphi_f(s)}\right] * e\right\}, $ | (8) |
其中, b+=(bTb)-1bT, ℓ-1表示Laplace逆变换, *表示卷积, φf(s)=ℓ[yf(t)], e表示系统与期望轨迹的误差。
2 基于UDE的反馈线性化控制器设计接下来分三个步骤设计控制器去实现含有不确定性和扰动的机械臂跟踪。(1)设计反馈线性化控制器实现机械臂的跟踪控制;(2)设计合适的滤波器估计无界扰动;(3)设计UDE控制器消除机械臂的不确定性和扰动。
2.1 反馈线性化控制器设计对于标称的机械臂系统(1), 可以改写为以下的形式:
| $ \ddot{q}=D^{-1}(q)[f-C(q, \dot{q})-G(q)], $ | (9) |
根据文献[15], 反馈线性化控制器设计如下: 对于系统(9), 不需要进行非线性变换, 可以得到线性反馈控制为:
| $ f = C(q, \dot q) + G(q) + D(q){\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{l}}}, $ | (10) |
其中, ul=[u1 u2]是输出闭环控制。把等式(10)带入到系统(9), 得到输入输出的线性解耦关系为:
| $ \ddot q = {\mathit{\boldsymbol{u}}_\mathit{\boldsymbol{l}}}, $ | (11) |
那么, 得到闭环控制ul为:
| $ {u_l} = \ddot x + {k_1}(\dot x - \dot q) + {k_2}(x - q){\rm{, }} $ | (12) |
其中, x∈R2表示机械臂系统的参考轨迹。
将式(12)代入式(11), 得到动力学跟踪误差表示如下:
| $ \ddot e + {k_1}\dot e + {k_2}e = 0, $ | (13) |
其中, e=x-q, e∈R2表示跟踪误差;k1, k2是为了达到预期跟踪性能选择的控制器增益。因此, 很容易得到上述反馈线性化控制器是成立的。
2.2 对于无界扰动滤波器的设计定理1 : 对于指数函数无界扰动d(t)=Aeat+C, 其中A, C是未知常数, a>0, 一个合适的滤波器表示为以下形式:
| $ G_f(s)=\frac{k}{s+k-a}, $ | (14) |
其中, k≫a>0, 通常取k=100a, 并且满足以下性质:
| $ \stackrel{\gg}{d}(t)=\ell^{-1}\left[G_f(s)\right]=d(t) * g_f(t) \rightarrow d(t), t \rightarrow \infty, $ | (15) |
其中, ℓ-1表示拉普拉斯反变换, *表示卷积。
证明: 由Gf(s)=ℓ[gf(t)]可得:
| $ g_f(t)=\ell^{-1}\left[G_f(s)\right]=k \mathrm{e}^{t(a-k)}, $ | (16) |
因此, 计算卷积得到:
| $ \begin{aligned} \left(A \mathrm{e}^{a t}+C\right) * g_f(t) & =A \mathrm{e}^{a t}+\mathrm{e}^{t(a-k)} \frac{(A k-A a+C k)}{(a-k)}-\frac{C k}{a-k} \\ & =\left(A \mathrm{e}^{a t}+C\right), t \rightarrow \infty。\end{aligned} $ | (17) |
所以, 我们设计的滤波器是合理的。
2.3 UDE控制器设计因为外部扰动的存在, UDE控制被用来抑制这些扰动, 改善跟踪控制的性能。带有扰动的机械臂动力学模型为:
| $ \ddot{q}=D^{-1}(q)[f-C(q,\dot{q})-G(q)]+\boldsymbol{d}+u_{\mathrm{UDE}}, $ | (18) |
其中, d=[d1, d2]T, uUDE是被设计的控制器。
根据引理1, 控制器uUDE可以表示为:
| $ u_{\mathrm{UDE}}=\ell^{-1}\left[\frac{G_f(s)}{1-G_f(s)}\right] *\left(D^{-1}(q)[f-C(q, \dot{q})-G(q)]\right)-\ell^{-1}\left[\frac{s G_f(s)}{1-G_f(s)} * e\right], $ | (19) |
其中, ℓ-1表示拉普拉斯逆变换;*表示卷积;滤波器Gf(s)在等式(14)给出。
那么, 在控制器u=ul+uUDE的作用下, 含有无界扰动的机械臂跟踪控制被实现。
3 数值仿真为了说明上述控制方法的有效性和正确性, 我们进行了数值仿真。机器人机械臂系统的详细参数如表 1所示。
| 表 1 机械臂仿真参数 |
 |
其他初始值选择如下: 机械臂的初始位置为: q=[0 0]T,
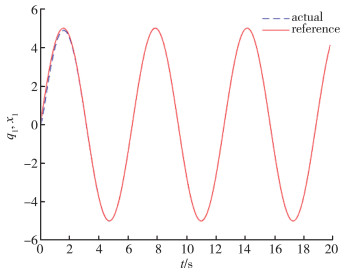 |
| 图 2 位置x1图 |
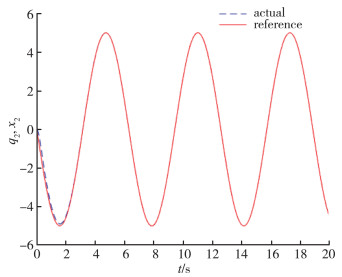 |
| 图 3 位置x2图 |
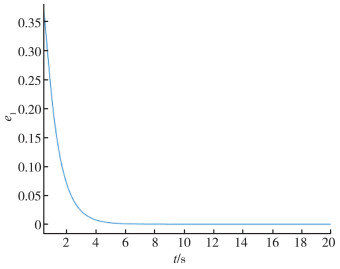 |
| 图 4 跟踪误差e1 |
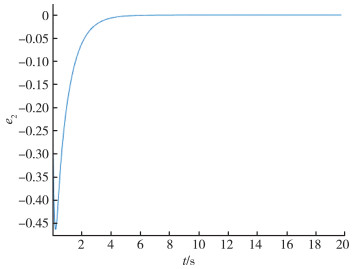 |
| 图 5 跟踪误差e2 |
 |
|
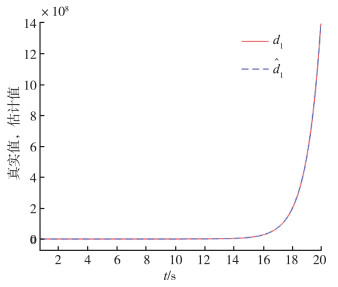
图 6 |
 |
|
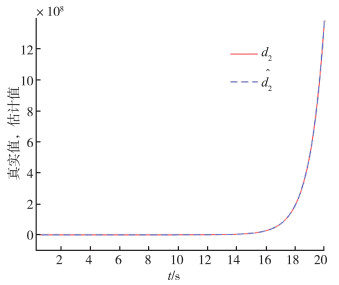
图 7 |
4 总结
针对复杂无界扰动下二自由度机械臂轨迹跟踪问题, 提出了基于UDE的反馈线性化控制策略。首先, 通过设计反馈线性化控制器实现了机械臂的跟踪控制;其次, 对于无界的外部扰动, 设计了基于UDE的控制器, 消除了扰动的影响;最后, 通过仿真验证了上述控制方法对机械臂跟踪控制的有效性和优越性。综上所述, 在无界扰动满足上述条件的情况下, 利用上述控制策略可以较好的控制机械臂到达期望位置, 实现无误差跟踪, 所提出的方法也可以用在其他机器人的控制领域。
| [1] |
葛俊, 童陆园, 耿俊成, 等. TCSC暂态过程中晶闸管导通角特性的研究[J]. 电网技术, 2001, 25(7/8): 18-22. |
| [2] |
韩江, 魏光耀, 董方方, 等. 打磨机器人自适应鲁棒约束跟踪控制[J]. 合肥工业大学学报(自然科学版), 2022, 45(7): 865-872. |
| [3] |
陶永, 兰江波, 刘海涛, 等. 基于滑模和模糊算法相融合的人机协作机器人轨迹跟踪方法[J]. 机械工程学报, 2022, 58(18): 181-191. |
| [4] |
WANG C S, WANG D, YAO Z. Neural network based adaptive dynamic surface control for omnidirectional mobilerobots tracking control with full-state constraints and input saturation[J]. International Journal of Control, Automation and System, 2021, 19(12): 4067-4077. DOI:10.1007/s12555-020-0582-7 |
| [5] |
DONG Y T, REN B B. UDE-Based variable impedance control of uncertain robot systems[J]. IEEE Trans.Systems, Man, and Cybernetics: Systems, 2019, 49(12): 2487-2498. DOI:10.1109/TSMC.2017.2767566 |
| [6] |
KANG Y T, XUE B, ZENG R Y. Self-Adaptive path tracking control for mobile robots under slippage conditions based on an RBF neural network[J]. Algorithms, 2021, 14(7): 196-210. DOI:10.3390/a14070196 |
| [7] |
陈浩华, 赵红, 王宁, 等. 复杂扰动下水下机器人的轨迹精确跟踪控制[J]. 中国舰船研究, 2022, 17(2): 98-108. |
| [8] |
杨亮, 陈勇, 刘治. 基于参数不确定机械臂系统的自适应轨迹跟踪控制[J]. 控制与决策, 2019, 34(11): 2485-2490. |
| [9] |
杨岸青, 李琳姗, 郭荣伟. 一类输入饱和受限线性系统的鲁棒控制[J]. 齐鲁工业大学学报, 2018, 32(6): 77-80. |
| [10] |
GUO R W, ZHAN G Y, JIANG C M. Synchronization of fractional-order chaotic systems with model uncertainty and external disturbance[J]. Mathematics, 2021, 9(8): 2074-2078. |
| [11] |
张特, 李世尧, 朱波. 内外不确定因素同时估计与补偿的鲁棒分布式跟踪控制[J]. 控制理论与应用, 2021, 38(7): 1033-1042. |
| [12] |
张国政, 张明明, 李新旻, 等. 基于不确定及扰动估计算法的永磁电机控制方法[J]. 天津工业大学学报, 2021, 40(3): 68-76. |
| [13] |
陈正升, 王雪松, 程玉虎. 考虑扰动与输入饱和的机械臂连续非奇异快速终端滑模控制[J]. 控制与决策, 2022, 37(4): 903-912. |
| [14] |
吴玉香, 李杨, 关伟鹏. 带有未知参数和有界扰动的机械臂混沌反控制[J]. 华南理工大学学报(自然科学版), 2018, 46(10): 63-71. |
| [15] |
KOLHE J P, SHAHEED M, CHANDAR T S, et al. Robust control of robot manipulators based on uncertainty and disturbance estimation[J]. International Journal of Robust and Nonlinear Control, 2013, 23(1): 104-122. |
 2023, Vol. 37
2023, Vol. 37


