| 基于双站交叉无人机纯方位无源定位问题研究 |
随着高新科学技术的蓬勃发展, 无人机运行操控技术发展突飞猛进。无人机集群在编队飞行时, 需要利用电磁波信号实现各无人机间的相互配合。若编队中一架或多架无人机出现“交流”故障, 若不能及时处理, 发生严重故障的无人机依然和编队中的无人机一起协同飞行, 将会直接影响整个编队飞行的安全。为避免各无人机间“交流”信息错误, 无人机需少向外发射电磁波信号, 即保持电磁静默。为迅速准确确定无人机位置, 目前主要采用纯方位无源定位技术, 即用无线电接收电子设备发射的电磁波来确定其位置。
近年来, 国内许多学者对无人机集群编队飞行进行了深入研究。无人机无源定位技术目前主要有三种: 测向交叉定位技术(angle of arrive AOA)、时差定位技术(time difference of arrival TDOA)、频差定位技术(frequency difference of arrival FDOA)。
关于AOA(测向交叉定位技术), 李铜川等[1]基于五种双站空间无源交叉定位的解析算法, 给出了影响无人机定位精度的影响因素。Noroozi A等[2]针对分布式多输入多输出雷达系统, 利用双基地距离测量, 提出并分析目标定位问题的代数闭式两阶段加权最小二乘解, 提高无人机较高噪声水平下的定位性能。张治等[3]提出一种利用两架或多架已知自身定位信息的无人机对空间非合作移动目标进行定位的优化算法。
关于TDOA(时差定位技术), Kovavisaruch等[4]建立了时差定位技术下的双迭代求解定位方程算法, 同时提出修正的Taylor级数法, 运用Newton-Gauss法对接收站的参数进行迭代估计。Fard H T等[5]用Taylor展开求解时差定位的最大似然问题完善定位方程解算问题的研究。Dexiu Hu等[6]对因多普勒压缩引发频差定位精度降低的问题给出一种以时差定位、频差定位为基础的差分多普勒速率估计方法。陈云龙[7]对无源时差定位方法中的时延估计算法进行优化, 设计并实现了一套无人机时差定位系统。韩璐潞[8]对基于时差与频差对无人机无源定位的精度给出提高方法。于小强[9]着重研究时差频差联合定位中定位参数估计、位置解算算法和目标跟踪滤波算法, 对联合时差频差算法进行仿真从而提升算法精度。王睿[10]以时差频差联合定位算法为蓝本, 构建新的双站无源定位模型, 在已构建的模型基础上建立双站运动对象的运动状态参数估计模型, 运用极大似然估计进行迭代算法研究。徐海源等[11]在多站无源定位系统中对信号抵达相异观测站的时差进行研究, 得出在一定观测时长时采用LSE方法能够提高时差模型精度的结论。
关于FDOA(频差定位技术), 孙浩宸[12]在双站无源定位的基础上建立了单站无源定位系统并对建立的系统进行模拟现实实验, 并联合频差定位技术与单站无源定位模型提出精确度更高的补偿TSWLS带来误差的算法。Karleigh Cameron Pine等[13]在传感器位置固定的情况下, 以频差定位涉及到的水平曲线、曲面模型为例, 描述了可行的远场时差和非等速到达时差数据。
本文主要采用纯方位无源定位方法实现无人机遂行编队飞行时的定位问题以及编队队形调整策略。首先, 考虑无人机编队基本信息, 确定发射信号和接收信号无人机的集合, 给出无人机所接收的方向信息;然后, 利用交叉定位方法, 建立基于“三点定圆”理论的双站交叉圆形编队无人机定位模型, 并将问题转化为相应的最小二乘问题;最后, 基于动态规划和贪婪策略给出圆形和相邻间距相等的锥形编队的具体调度方案。
1 无人机编队基本信息考虑由m架无人机组成编队飞行集群, 其中(m-1)架无人机(编号设为FY01-FY0(m-1))按编号顺序分布, 剩余1架无人机(编号设为FY00)位于中心。假设发射信号无人机位置无偏差, 接收信号无人机位置略有偏差;被动接收信号的无人机, 它的接收方向信息为该无人机与任意两架发射信号无人机连线之间的夹角, 如图 1所示。
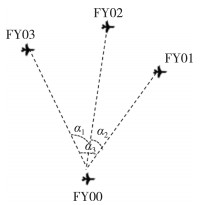 |
| 图 1 方向信息示意图 |
记集合K为发射信号无人机集合。不失一般性, 假设FY00、FY01为发射信号无人机, 另有k架无人机发射信号(记编号为FY0k1, FY0k2, …,FY0kk), 则K={FY00, FY01, FY0k1, FY0k2, …,FY0kk}。
记集合N为接收信号无人机集合。则N中共有(m-k-2)个元素, 可记为N={FY0n1, FY0n2…,FY0nm-k-2}。
无人机接收方向信息为该无人机与任意两架发射信号无人机连线之间的夹角, 不妨设FY0nj与FY00、FY01间夹角分别为αj1, FY0nj与FY00、FY0k1间夹角为αj2, FY0nj与FY00、FY0k2间夹角为αj3…, FY0nj与FY00、FY0kk间夹角为αj(k+1), FY0nj与FY01、FY0k1间夹角为αj(k+2), …, FY0nj与FY0kk-1、FY0kk间夹角为αj((k+2)(k+3)/2)。
2 基于“三点定圆”理论的双站交叉圆形编队无人机定位模型交叉定位是通过两个及两个以上高精度侦测设备在观测点或者观测站对同一个辐射源进行测向, 然后由各观测站测量得到的多条方位线交会点确定辐射源位置即确定目标与定位站之间距离的定位方法。
在m架无人机飞行高度一致且均匀分布形成圆形编队的情况下(图 2), 通过接收方向信息实现对无人机定位。假设圆周半径为R, 圆周以无人机FY00所在位置为原点, 以FY00为端点且经过FY01的射线为正半轴(下面简记为FY00-FY01)建立坐标系。无人机FY01对应的坐标为(R, 0);任一发射信号无人机FY0ki坐标为(R, (ki-1)θ), 其中θ=2π/(m-1);任一接收信号无人机FY0nj坐标为(xj, βj), 其中xj表示FY0nj与原点之间的距离, βj表示FY00-FY0nj与FY00-FY01之间的夹角。
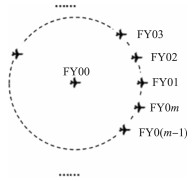 |
| 图 2 圆形无人机编队示意图 |
2.1 三角定位法求解坐标
分别在以FY00、FY01和FY0nj为顶点和以FY00、FY0ki和FY0nj为顶点的三角形中, 利用正弦定理可得
| $ \begin{cases}\frac{\sin \alpha_{j 1}}{R}=\frac{\sin \left(\pi-\beta_j-\alpha_{j 1}\right.}{x_j} & \beta_j \in(0, \pi] \\ \frac{\sin \alpha_{j 1}}{R}=\frac{\sin \left(\pi-\left(2 \pi-\beta_j\right)-\alpha_{j 1}\right.}{x_j} & \beta_j \in(\pi, 2 \pi) \\ \frac{\sin \alpha_{j(i+1)}}{R}=\frac{\sin \left(\pi-\left|\beta_j-\left(k_i-1\right) \theta\right|-\alpha_{j(i+1)}\right.}{x_j} & \alpha_{j 1}<\alpha_{j(i+1)} \\ \frac{\sin \alpha_{j(i+1)}}{R}=\frac{\sin \left(\pi-\left(2 \pi-\beta_j\right)-\left(k_i-1\right) \theta \mid-\alpha_{j(i+1)}\right.}{x_j} & \alpha_{j 1}<\alpha_{j(i+1)}\end{cases}。$ | (1) |
由方程组(1)即可解得任一无人机FY0nj坐标(xj, βj)。
2.2 “三点定圆”双站交叉无人机定位模型任一接收信号无人机FY0nj∈N, FY0nj参数坐标表示为(Rcos γi, Rsin γi)。
(1) FY0ki、FY0ki、FY0nj三点确定⊙O1, 记为(x-x1)2+(y-y1)2=r12。
由FY00(0, 0)、FY0nj(Rcos γi, Rsin γi)在⊙O1上可得
| $ \left(R \cos \gamma_i-x_1\right)^2+\left(R \sin \gamma_i-y_1\right)^2=r_1^2, $ | (2) |
| $ x_1^2+y_1^2=r_1^2。$ | (3) |
在以FY0ki、FY0ki、O1为顶点的三角形中应用余弦定理可得
| $ \cos \left(2 \alpha_{j(i+1)}\right)=\left(2 r_1^2-R^2\right) / 2 r_1^2。$ | (4) |
联立式(2)、(3)、(4)可得圆心O1(x1, y1)和半径r1。
(2) FY00、FY01、FY0ni三点确定⊙O2, 记为方程(x-x2)2+(y-y2)2=r22, 则
| $ \left\{\begin{array}{l} x_2^2+y_2^2=r_2^2 \\ \left(R-x_2\right)^2+y_2^2=r_2^2 \\ \cos \left(2 \alpha_{j 1}\right)=\left(2 r_2^2-R^2\right) / 2 r_2^2 \end{array}\right.。$ | (5) |
由方程组(5)式可得圆心O2(x2, y2)和半径r2。
(3) FY01i、FY0ki、FY0nj三点确定⊙O3, 记为(x-x3)2+(y-y3)2=r32, 则
| $ \left\{\begin{array}{l} \left(R \cos \gamma_i-x_3\right)^2+\left(R \sin \gamma_i-y_3\right)^2=r_3^2 \\ \left(R-x_3\right)^2+y_3^2=r_3^2 \\ \left(R-x_3\right)^2+\left(\left(k_i-1\right) \theta-y_3\right)^2=r_3^2 \end{array}, \right. $ | (6) |
由方程组(6)可圆心O3(x3, y3)和半径r3。
无人机⊙O1所在位置即为三圆交点(图 3), 联立⊙O1、⊙O1、⊙O3方程, 可得
| $ \left\{\begin{array}{l} \left(x-x_1\right)^2+\left({ }^y-y_1\right)^2=r_1^2 \\ \left(x-x_2\right)^2+\left({ }^y-y_2\right)^2=r_2^2 \\ \left(x-x_3\right)^2+\left(y-y_3\right)^2=r_3^2 \end{array}\right.。$ | (7) |
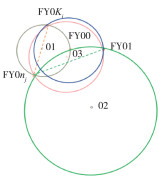 |
| 图 3 模型示意图 |
方程(7)可写为矩阵形式
| $ \left[\begin{array}{ccc} -2 x_1 & -2 y_1 & 1 \\ -2 x_2 & -2 y_2 & 1 \\ -2 x_3 & -2 y_3 & 1 \end{array}\right]\left[\begin{array}{c} x \\ y \\ x^2+y^2 \end{array}\right]=\left[\begin{array}{c} r_1^2-\left(x_1^2+y_1^2\right) \\ r_2^2-\left(x_2^2+y_2^2\right) \\ r_3^2-\left(x_3^2+y_3^2\right) \end{array}\right], $ | (8) |
将上述方程记为
| $ \boldsymbol{A} \boldsymbol{X}=\boldsymbol{B}, $ | (9) |
其中,A=
此时, FY0nj坐标可以转化为求解最小二乘问题
| $ \min\limits_X\|\boldsymbol{B}-\boldsymbol{A} \boldsymbol{X}\|_2^2。$ | (10) |
由最小二乘法得X=(ATA)-1ATB。
2.3 基于动态规划的圆形编队位置调整策略圆形编队位置调整分为两个阶段。
(1) 阶段1:使得(m-1)架无人机分布在同一圆周上。
以10架无人机形成圆形编队情况为例, 无人机初始位置如表 1。
| 表 1 无人机初始位置信息 |
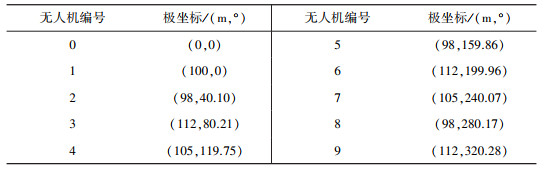 |
已知FY02、FY05、FY08均在半径为98 m的圆周上, 不妨选取圆心为FY00。假设无人机FY00、FY02、FY05为发射信号无人机。本阶段目标为将其余无人机通过多次调整使分布在该圆周上。以调整FY06位置为例, 假设FY06初始坐标为(x6, β6), 其中x6≠98,
(2) 阶段2:使得(m-1)架无人机呈编队队形飞行。
在无人机已经分布在圆周的基础上, 调整(m-1)架无人机位置使其呈编队队形飞行。以调整FY06位置为例, 根据无人机FY06接收到的方向信息, 将β6调整为
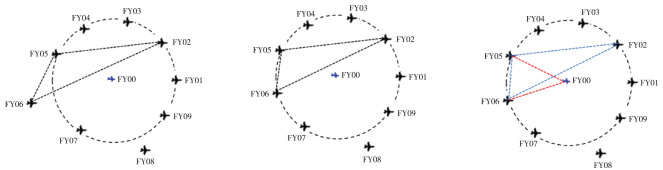 |
| 图 4 演示操作示意图 |
上述圆形编队位置调整策略可由表 2所示。
| 表 2 圆形编队位置调整策略 |
 |
2.4 基于贪婪策略的锥形编队位置调整策略
无人机实际飞行中, 编队队形可以为任意形状, 针对锥形编队队形如图 5所示, 直线上相邻两架无人机间距相等, 仍考虑纯方位无源定位的情形, 设计无人机位置调整方案。
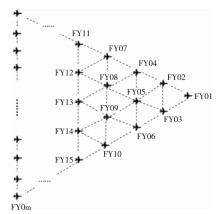 |
| 图 5 无人机锥形编队示意图 |
无人机飞行时不一定保持在同一高度且初始位置未知。为了使无人机形成直线上相邻两架无人机间距相等的锥形编队, 首先需要调整无人机飞行高度, 使所有无人机保持同一高度飞行;然后调整无人机位置, 使所有无人机形成锥形编队。在选择时, 应尽可能选择相邻三架及以上无人机发射信号, 通过相邻无人机之间距离和角度来衡量无人机位置偏差, 从而可以达到调整无人机位置的效果。
采用贪婪策略, 每次选择数量尽可能少的无人机进行发射信号, 就可达到调整其余无人机位置的目的。贪婪策略一般涉及到最优子结构, 是对问题进行求解时, 在每一步中都选择最优(即最有利)的选择, 希望能够导致总体结果最优的算法。也就是说, 贪婪策略在求解问题时, 不从整体最优进行考虑, 仅得到某种意义上的局部最优解。在应用贪婪算法时, 首先需要根据目标, 对问题进行排序;然后根据排序选择最优子集合, 每步总是选择当前最优的选择, 得到局部最优解。
2.4.1 FY01的调整选择无人机FY02、FY03发射信号, 如图 6所示。
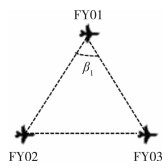 |
| 图 6 FY02、FY03发射信号示意图 |
在此情况下, 只需将角β1调整为
为了使调整后的无人机在同一高度, 根据贪婪算法, 应选择FY01相邻无人机进行下一步调整, 即选择FY02或FY03。不失一般性, 我们以FY02为例, FY03的调整策略同理可得。
2.4.2 FY02的调整(1) 选择无人机FY01、FY02发射信号, 如图 7所示。
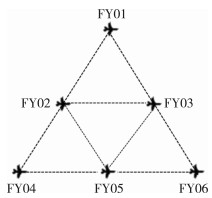 |
| 图 7 FY01、FY02发射信号示意图 |
调整FY04位置, 使其与FY01、FY02在同一条直线上, 此时完成对无人机FY04飞行高度的调整, 接下来考虑FY02与FY04、FY05间夹角问题。
(2) 选择无人机FY01、FY03、FY04发射信号, 如图 8所示。
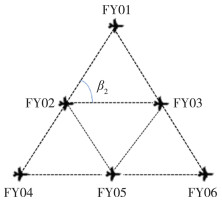 |
| 图 8 FY01、FY03、FY04发射信号示意图 |
(3) 将无人机FY02沿FY01-FY04构成直线方向移动, 将β2调整为
(4) 同理对FY03进行调整, 即可实现FY01、FY02、FY03在平面上等距分布。根据贪婪算法选择FY02相邻无人机进行调整。无人机FY05仅需一次调整就可实现FY01、FY02、FY03、FY05等距分布, 因此选择对FY05进行位置调整。
2.4.3 FY05的调整选择无人机FY01、FY02、FY03发射信号(如图 9所示)
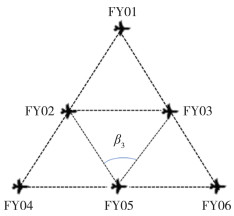 |
| 图 9 FY01、FY02、FY03发射信号示意图 |
将β3调整为
同理对FY04进行调整, 即可实现FY01-FY05在平面上等距分布。
2.4.4 剩余无人机位置的调整同理, 可以将无人机FY06-FY0m调整为直线上相邻两架无人机间距相等的锥形队形。
通过以上步骤即可完成将所有无人机调整为直线上相邻两架无人机间距相等的锥形编队队形。
上述锥形编队位置调整策略可由表 3所示。
| 表 3 锥形编队位置调整策略 |
 |
3 结论
本文主要解决无人机遂行编队飞行中的定位和位置调整策略问题, 采用简单直接的纯方位无源定位方法, 以保证无人机集群在遂行编队飞行时可以快速准确定位无人机位置并将其调整到理想位置。仅对无人机编队的两种特殊的情况进行了分析, 在实际情况中, 无人机编队飞行时的形状应是多变且复杂, 同时飞行情况受很多环境因素的影响, 未来需要对更复杂的情况进行分析研究。
| [1] |
李铜川, 黄剑伟, 陈俊吉, 等. 几种双站无源被动交叉定位模型及其误差分析[J]. 四川兵工学报, 2014, 35(8): 137-140. |
| [2] |
NOROOZI A, SEBT M A, OVEIS A, et al. Improved algebraic solution for elliptic localization in distributed MIMO radar[C]//Sadjad University of Technology. 26th Iranian Conference on Electrical Engineering, Iran, Mashhad: 2018.
|
| [3] |
张治, 卢鸿谦, 马懿超, 等. 一种基于AOA模型的多机协同无源定位优化算法[C]//上海大学. 第40届中国控制会议论文集(15), 中国, 上海: 2021.
|
| [4] |
KOVAVISARUCH L, HO K C. Alternate source and receiver location estimation using TDOA with receiver position uncertainties[C]//IEEE. International Conference on Acoustics, Speech and Signal Processing, Australia, Calgary: 2005.
|
| [5] |
FARD H T, ATASHBAR M, NOROUZI Y, et al. Multi references TDOA-based source localization[J]. Turkish Journal of Electrical Engineering and Computer Sciences, 2013, 21(7): 1920-1929. |
| [6] |
DEXIU H, HUANG Z, ZHANG S, et al. Joint TDOA, FDOA and differential doppler rate estimation: method and its performance analysis[J]. Chinese Journal of Aeronautics Chinese J Aeronaut, 2018, 31(1): 137-147. DOI:10.1016/j.cja.2017.11.005 |
| [7] |
陈云龙. 无人机无源时差定位方法研究及实现[D]. 西安: 西安电子科技大学, 2021.
|
| [8] |
韩璐潞. 基于时差和频差的无人机对干扰辐射源无源定位研究运用[J]. 中国新通信, 2021, 23(19): 62-63. |
| [9] |
于小强. 基于时差频差的多机无源定位及跟踪算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
|
| [10] |
王睿. 运动双站时频差定位方法研究[D]. 成都: 电子科技大学, 2021.
|
| [11] |
徐海源, 苏成晓, 刘亚奇. 运动多站无源定位中的时差及其变化率估计方法[J]. 电子信息对抗技术, 2022, 37(3): 26-30. |
| [12] |
孙浩宸. 单站无源目标定位方法研究[D]. 哈尔滨: 东北林业大学, 2020.
|
| [13] |
PINE K C, PINE S J, CHENEY M. The geometry of far-field passive source localization with TDOA and FDOA[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57: 3782-3790. |
 2023, Vol. 37
2023, Vol. 37


