| 晶粒尺寸效应对7075铝合金热变形不均匀性的影响 |
鉴于双碳时代主题和节能减排发展趋势, 使用轻质高强度铝合金替代钢材作为汽车板材覆盖件的趋势越来越明显[1]。在变形高强度铝合金中, 7系(Al-Zn-Mg-Cu)合金具有比强度高、抗应力腐蚀等优良特性[2]。7系铝合金(Al-Zn-Mg-Cu)属于可热处理强化的铝合金, 在经T6热处理后抗拉强度可达500 MPa以上。对汽车、航空航天用7系铝合金板材多使用帝国理工学院林建国等[3]开发的成形-淬火一体化技术。但7系铝合金在热冲压过程中材料性能会严重降低, 因此如何将热冲压工艺应用到新能源汽车板材覆盖件的成形过程是国内外研究的热点。
7075铝合金热成形过程中影响塑性相关的因素有热处理工艺、温度、晶粒尺寸与晶粒形貌等。其中在温度和热处理工艺相同的情况下, 可以通过改善晶粒尺寸和晶体形貌来保证强度并且提高塑性, 改善成形性[4]。对于晶粒尺寸等组织演变对板材成形过程中宏观流变行为会产生的影响, 目前已有众多研究[5-9]。研究表明, 流动应力随晶粒尺寸的增大而减小, 通过这些研究可以了解金属材料塑性变形的特性。为了确定最佳的7075铝合金成形条件, 研究人员对7075铝合金的高温塑性进行了广泛的研究, 但大多数工作都集中在温度、应变速率等方面[10-12]。近年来, 国内外学者开始探索晶粒尺寸和晶体形貌对7075热加工行为的形象。Li等[13]通过改进粘塑性本构模型模拟7075T型件在热冲压过程中的晶粒尺寸演变过程, 得出随变形速率降低和变形温度的升高, 晶粒尺寸逐渐减小产生细晶强化现象, 屈服和抗拉强度提高。
影响7075铝合金热成形过程中塑性变形的因素还有位错等晶体缺陷。研究表明热成形过程中预先产生的析出相和残留的位错在很大程度上影响铝合金的塑性变形过程[14-17]。为了描述多晶材料中存在的各向异性塑性变形影响因素, Roters等[18]晶体塑性中与位错密度相关的理论与有限元方法结合起来, 研究了位错-位错相互作用和位错-沉淀相互作用对加工硬化的影响, 在等温条件下考虑了第二相粒子的沉淀和形核影响可动位错平均自由程, 建立了基于三个内部变量的多晶显微组织应变硬化模型, 结果表明, 所构建的本构关系在位错密度演化规律中明确使用了主动滑移系数, 模型特别适合晶体塑性有限元模拟, 为后续基于位错密度的晶体塑性模型提供基础。
经过长时间的发展, 使用晶体塑性模型来描述材料变形过程中位错滑移和变形孪晶等塑性变形机制变得较为成熟。作为将宏观变形与材料微观组织联系起来的节点, 晶体塑性方法在指导材料设计与优化成形工艺等方面发挥着愈发明显的作用。在使用晶体塑性理论仿真模拟材料塑性变形过程中, 晶粒尺寸对微观组织演化的影响是当前研究的热点。Hanamura等[19]研究了马氏体钢种奥氏体晶粒尺寸对马氏体相变的影响, 研究表明随着奥氏体晶粒尺寸的细化, 抗拉强度略有增加, 奥氏体的细化大大增强了马氏体的断裂应变。Shang等[20]通过使用全场晶体塑性有限元模拟与创建具有真实晶粒结构和孔洞的高分辨率RVE研究了晶粒尺寸对316LN奥氏体钢微孔洞和宏观断裂的影响, 得出随着晶粒尺寸增大, 变形的非均匀性增大, 孔洞长大的分散性增大。
本文基于位错密度演化的晶体塑性模型模拟7075铝合金板材热拉伸过程中应力应变、位错密度演化等过程, 研究了不同晶粒尺寸在热拉伸过程中微观组织演化及力学性能的影响, 通过真应力-应变曲线验证了所用位错密度晶体塑性模型的正确性, 并通过使用所构建的位错密度本构模型对含有不同晶粒尺寸的RVE模型进行热拉伸仿真模拟, 获得应力集中区域与与位错密度较大区域分布统一, 并随着晶粒尺寸的增大, 应力与应变不均匀现象加重。
1 试样制备与试验方法为了揭示晶粒尺寸对热拉伸过程中微观组织和力学性能的影响, 实验方案使用AA7075-T6高强铝合金板材具体成分如表 1所示。采用热模拟机Gleeble-3000C研究了AA7075-T6板材在高温下的流变行为。所采用的狗骨试样使用激光切割机切割而成, 如图 1所示, 激光切割方向与轧制方向平行。所得的激光切割试样都用400-和600-SiC砂纸对边缘进行光滑抛光。
| 表 1 7075-T6铝合金材料化学成分表 |
 |
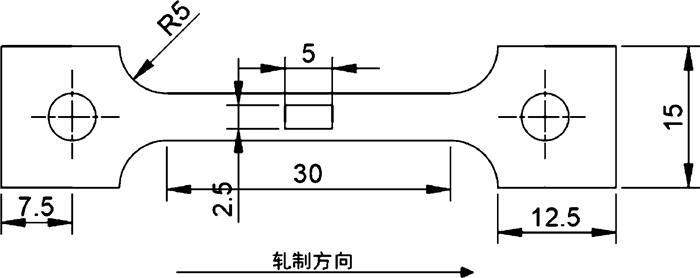 |
| 图 1 所用7075-T6板材热拉伸试样 |
热变形工艺如下: 在623、673和723 K温度下对平行于轧制方向的试样进行一系列的单向拉伸试验至断裂。随后样品在水中淬火, 以保留在高温下变形微结构的特征。
利用JSM-7900F型号扫描电镜对断裂试样并进行了电子背散射衍射测试(EBSD), 如图 2所示。设置电压为20 kV, 采集速度为308.35 Hz, 以便进行晶粒尺寸的计算以及晶体学取向的分析, 不同温度下断裂样本的晶体学取向如图 3所示。通过图 3可以看出, 在不同温度下单向拉伸至断裂的样品整体与拉伸方向呈45°, 晶体形貌由等轴晶变为细长的链状、柱状晶。随着温度的升高, 试样内部出现了大量细小的晶粒, 这些细小晶粒的平均尺寸为11 μm。
 |
| 图 2 所构建的具有真实取向的RVE模型及仿真边界条件 |
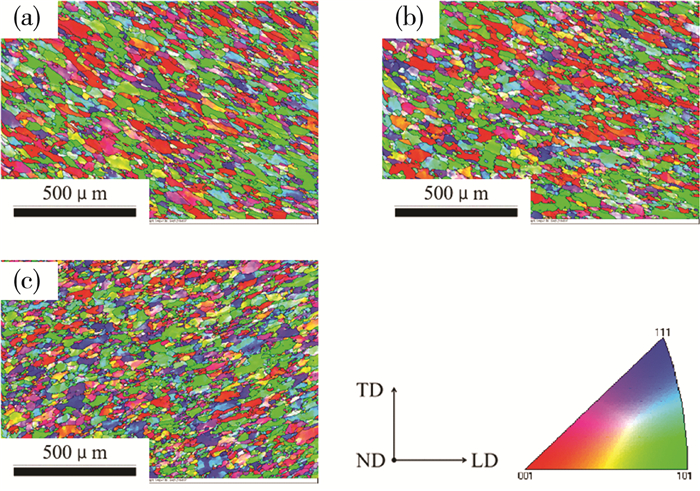 |
| 注: (a)623 K; (b)673 K; (c)723 K。 图 3 不同温度下单向拉伸7075铝合金的反极图 |
2 基于位错密度的晶体模型
在晶体塑性理论中, 材料的变形梯度F由弹性变形梯度Fe与塑性变形梯度Fp给出,
| $ F=F_{\mathrm{e}} F_{\mathrm{p}}, $ | (1) |
其中, 中间构型的非弹性形变梯度Fp可以塑性变形速度梯度Lp表示如下,
| $ F_{\mathrm{p}}=L_{\mathrm{p}} F_{\mathrm{p}}, $ | (2) |
由GREEN-LAGRANGE应变E与第二P-K应力通过弹性刚度¢联系起来, 表现形式为:
| $ S=\not \subset: E, $ | (3) |
位错滑移通过影响中间构型的非弹性形变的速度梯度进而影响材料的塑性变形, α剪切系的塑性本构形式表现为:
| $ L_{\mathrm{p}}=\sum\limits_\alpha \gamma^a\left(\boldsymbol{S}_s^a \otimes \boldsymbol{n}_s^a\right), $ | (4) |
其中Ssa和nsa代表剪切方向和剪切平面法线的单位矢量。对于不同的晶格类型, 需要选择指定的滑移系, 例如面心立方fcc晶体的滑移方向为<011>, 平面法线为{111}。体心立方拥有两个滑移系<111>{011}与<111>{211}。
传统的唯象塑性流动法则使用了参考剪切速率和剪切速率敏感性指数, 无法在微观层面描述位错的滑移、交割与湮灭。根据Ma[21]所提出的一种基于位错滑移的流动规律所包括的关于位错密度和温度相关的参考剪切速率, 构建了新的关于位错密度演化的流动法则。
| $ \dot{\gamma^a}=\left\{\dot{\gamma}_0^a \exp \left[-\frac{Q \operatorname{slip}}{k_B T}\left(1-\frac{\left|\tau^a\right|-\tau_{\text {pass }}^a}{\tau_{\text {cut }}^a}\right)\right] \operatorname{sign}\left(\tau^a\right), \begin{array}{l} \left|\tau^a\right|>\tau_{\text {pass }}^a \\ \left|\tau^a\right| \leqslant \tau_{\text {pass }}^a \end{array} \right.。$ | (5) |
由平行位错引起的通过应力计算如下:
| $ \tau_{\text {pass }}^\alpha=G b_s^a\left(\sum\limits_{\alpha=1}^{N_s} \boldsymbol{h}^{\alpha \alpha}\left(\vartheta^a+\vartheta_{\mathrm{dj}}^a\right)\right)^{\frac{1}{2}}, $ | (6) |
其中G为剪切模量, hαα′为两个滑移系统之间的交互作用矩阵, Qslip时位错滑移的有效活化能[22]。
位错密度的演化与位错的增殖、湮灭以及偶极子的形成密切相关, 可以由如下公式给出:
| $ \dot{\vartheta}=\frac{|\dot{\gamma}|}{b_s {\mathit{\Lambda}}_s}-\frac{2 \hat{d}}{b_s} \vartheta|\dot{\gamma}|, $ | (7) |
| $ \dot{\vartheta}=\frac{2(\mathop d\limits^ \wedge -\mathop d\limits^ \vee )}{b_s} \vartheta|\dot{r}|-\frac{2 \mathop d\limits^ \vee}{b_s} \vartheta_{\mathrm{di}}|\dot{r}|-\vartheta_{\mathrm{di}} \frac{4 v_{\mathrm{cl}}}{\hat{d}-d}。$ | (8) |
在上述公式中, 第一个公式对应位错密度增加和由于偶极子形成而位错密度减少。
第二个公式对应位错偶极子的形成, 以及具有位错的偶极子的自发湮灭以及由于位错攀移引起的位错偶极子的湮灭。位错攀移速率由以下公式给出:
| $ v_{\mathrm{cl}}=\frac{G D_0 V_{\mathrm{cl}}}{\pi(1-v) k_B T} \frac{1}{\mathop d\limits^ \wedge - \mathop d\limits^ \vee } \exp \left(-\frac{Q_{\mathrm{cl}}}{k_B T}\right), $ | (9) |
其中D0是自扩散系数前因子; Vcl是攀移激活体积; Qcl是攀移激活能;
| $ \mathop d\limits^ \wedge=\frac{3 G b_s}{16 {\rm{ \mathit{ π}}}|\gamma|}, $ | (10) |
| $ \stackrel{\vee}{d}=D_a b_s, $ | (11) |
其中Da是拟合参数。
在Kocks-Mecking模型中[23], 位错密度是描述硬化行为的主要状态变量。应变硬化描述的位错平均自由程表示由于晶界前位错的堆积、位错-位错相互作用、孪晶的形成和马氏体的形成[24]。
| $ \frac{1}{{\mathit{\Lambda}}_{\mathrm{s}}}=\frac{1}{D}+\frac{1}{\lambda_{\mathrm{s}}}+\frac{1}{\lambda_{\mathrm{tw}}}+\frac{1}{\lambda_{\mathrm{tr}}}, $ | (12) |
在本研究中可以简化为:
| $ \frac{1}{{\mathit{\Lambda}}_{\mathrm{s}}}=\frac{1}{D}+\frac{1}{\lambda_{\mathrm{s}}}, $ | (13) |
| $ \frac{1}{\lambda_s^a}=\frac{1}{i_{\mathrm{s}}}\left(\sum\limits_{a=1}^{N_{\mathrm{s}}} p^{a a^{\prime}}\left(\vartheta^{a^{\prime}}+\vartheta_{\mathrm{di}}^{a^{\prime}}\right)\right)^{\frac{1}{2}}, $ | (14) |
其中D是平均晶粒尺寸, is是拟合参数, paa′是对林位错密度的预测。
3 实验与仿真结果 3.1 本构模型验证从图 4可以看出, 通过使用基于位错密度的晶体塑性模型, 模拟不同温度下7075铝合金的力学行为, 并与热拉伸实验的流变性为相结合, 可知, 基于微观物理参数所构建的位错密度本构模型能够较为准确地描述7075铝合金在不同温度下的宏观塑性变形程度与力学响应。
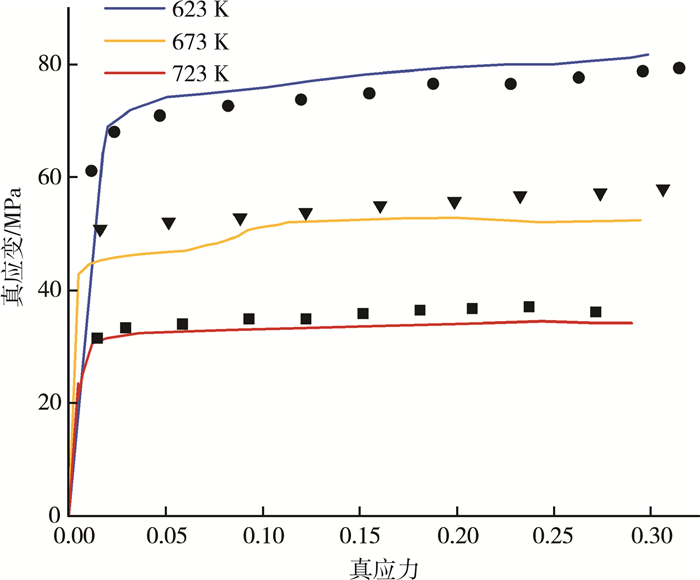 |
| 图 4 使用具有真实取向的RVE模型与实验对比的真应力-应变曲线 |
图 5为所构建具有真实取向平均晶粒尺寸为10 μm的准三RVE模型位错密度、等效应变和Mises应力分布云图。从图 5(a)、(c)所示, RVE模型在单轴拉伸过程中位错密度和应力分布不均, 在图中红色圈出的部分出现了明显的位错塞积和应力集中现象。结合具有真实取向RVE模型反极图, 可解释应力与位错分布不均的原因是不同晶粒间的取向不同。在单向拉伸过程中, 材料的表面变得粗糙, 出现许多沟槽与脊状形状, 在图 5(b)可以看到, RVE模型中均匀分布着许多与拉伸方向呈45°左右的局部剪切带和应变集中区域(图中黄色线条内)。
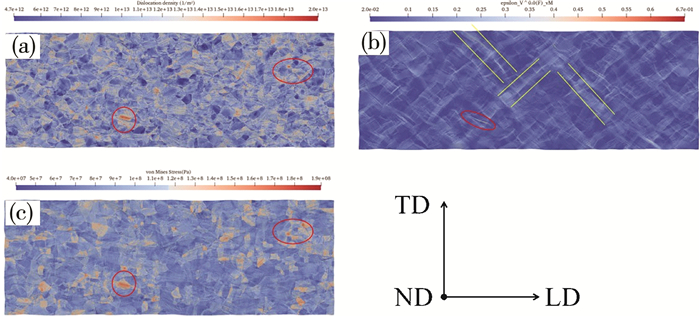 |
| 注: (a)位错密度; (b)等效应变; (c)Mises。 图 5 工程应变为7%时应力分布云图 |
3.2 RVE建模与力学响应分析
为了考虑不同晶粒尺寸对微观结构演化与力学性能的影响, 使用Dream3D软件生成了含有不同晶粒尺寸的准三维RVE模型如图 6所示, 建立模型大小为1 500 μm×600 μm×1 μm。由于厚度远小于长宽, 因此本研究的重点是长宽平面内的变形行为。其中模型1为具有实验所得取向的模型平均晶粒尺寸为10 μm, 模型2、模型3和模型4的平均晶粒尺寸为20、35和50 μm, 不同晶粒尺寸的分布图如图 7所示。对所建立模型使用DAMASK开源软件在恒定623、673和723 K温度下, 每个RVE在规定的总变形梯度F和第一P-K应力见公式(15), 下拉伸至应变0.3, 所用模拟RVE与边界条件如图 2所示。
| $ \bar{F}=\left[\begin{array}{ccc} 0.01 & 0 & 0 \\ * & * & 0 \\ 0 & 0 & 1.0 \end{array}\right] \text { 和 } \bar{P}=\left[\begin{array}{ccc} * & * & * \\ 0 & 0 & * \\ * & * & * \end{array}\right] \text {, } $ | (15) |
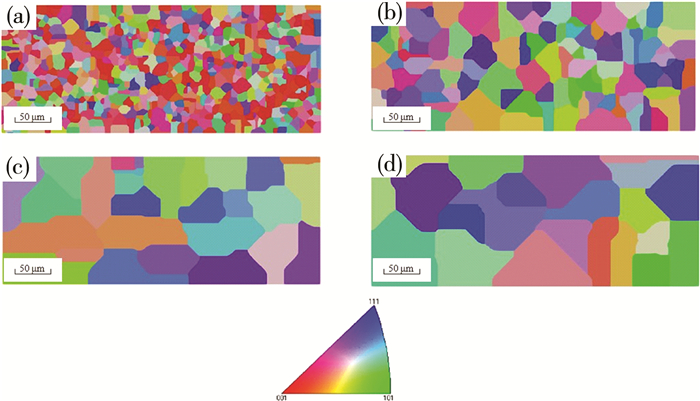 |
| 注: (a)具有真实取向, 平均晶粒尺寸10 μm; (b)(c)(d)随机取向, 平均晶粒尺寸为20、35和50 μm。 图 6 不同晶粒尺寸RVE模型 |
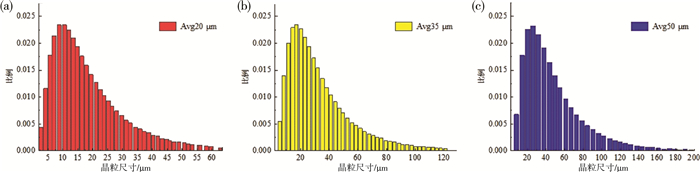 |
| 注: (a)20 μm; (b)35 μm; (c)50 μm。 图 7 晶粒尺寸分布曲线 |
式中*代表未定义的项目, 给出了方程中应用变形条件, 仿真过程不考虑厚度方向的应变, 厚度方向的晶粒形貌是不变的。
不同晶粒尺寸RVE模型的位错密度分布如图 8所示, 从图 8可以看出, 随着平均晶粒尺寸的增大, 位错密度由较为均匀分布转变为不均匀分布。在拉伸过程中, 伴随着晶体的旋转和形变以及局部剪切带的形成, 大量的位错由于晶界的存在引入了几何非必要位错, 而由于这些位错与初级位错之间的相互作用引起了位错的局部增殖, 进而产生整体位错密度分布不均匀现象。此外, 相同尺寸的RVE模型中含有较少量大尺寸的晶粒会导致不同晶粒间的接触晶界相对较小晶粒之间扩大化, 进而位错密度的不均匀性更容易出现在两个大尺寸晶粒之间。
 |
| 注: (a)10 μm; (b)20 μm; (c)35 μm; (d)50 μm。 图 8 不同晶粒尺寸RVE模型在等效应变7%时位错密度分布云图平均晶粒尺寸 |
图 9代表各晶粒尺寸下的等效应变分布云图。从图 9(b)和图 10(d)可以看出, 晶粒尺寸为20 μm的模型中应变分布相较图 9(d)分布更加均匀, 且出现相对较小应力集中区域, 而晶粒尺寸为50 μm的模型中出现了较多与拉伸方向呈45°的局部应变集中区域(图中圈出部分), 而较为均匀的应变分布有利于变形协调。
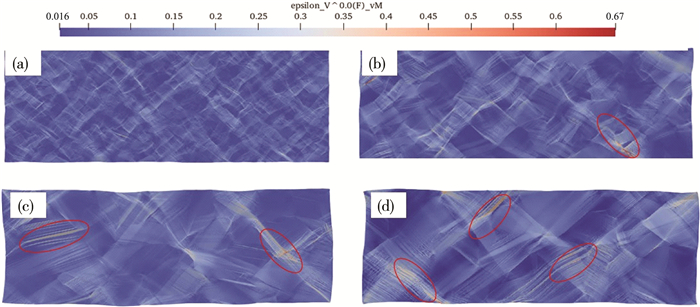 |
| 注: (a)10 μm; (b)20 μm; (c)35 μm; (d)50 μm。 图 9 不同晶粒尺寸RVE模型在应变10%时等效应变分布云图平均晶粒尺寸 |
4 结论
本文通过将基于位错密度演化的晶体塑性模型, 建立了不同晶粒尺寸的7075铝合金准三维RVE模型, 研究了不同晶粒尺寸对7075铝合金热拉伸过程中微观组织演化及力学响应的影响, 得出以下结论:
1) 提高热成形温度可通过细晶强化增强7075铝合金的力学性能。随着热变形温度从350 ℃升高到450 ℃, 7075铝合金的屈服强度从75 MPa降低到30 MPa, 平均晶粒尺寸从25 μm降低到16 μm。
2) 在相同晶粒尺寸下, 模拟所构建的基于统计学具有真实取向的准三维RVE模型中位错密度整体分布均匀, 且位错密度集中区域与应力集中区域吻合。
3) 不同晶粒尺寸的位错密度和应力应变分布不同。平均晶粒尺寸为50 μm的RVE模型比平均晶粒尺寸为20 μm的模型在模拟过程中出现了相对较多与拉伸方向呈45°的应变集中区域, 其中平均晶粒尺寸为50 μm的最大局部应变为0.6, 平均晶粒尺寸为20 μm的最大局部应变为0.35, 且伴随着晶粒尺寸增大, 局部应变集中现象加重。
4) 相较于晶粒尺寸粗大的7075铝合金材料, 晶粒尺寸细小的材料应力应变分布均匀, 更适合高温热变形工艺。
| [1] |
陈小明, 宋仁国, 李杰. 7xxx系铝合金的研究现状及发展趋势[J]. 材料导报, 2009, 23(3): 67-70. |
| [2] |
YOSHIDA H, NORIKANE K, HAYASHI M. Recent trend of development in aluminum alloys for aircraft[J]. Japan Inst.Light Metals, 2015, 65(9): 441-454. DOI:10.2464/jilm.65.441 |
| [3] |
LI C M, ZENG S M, CHEN Z Q, et al. First-principles calculations of elastic and thermodynamic properties of the four main intermetallic phases in Al-Zn-Mg-Cu alloys[J]. Computational Materials Science, 2014, 93: 210-220. DOI:10.1016/j.commatsci.2014.06.031 |
| [4] |
WILLIAMS J C, STARKE JR E A. Progress in structural materials for aerospace systems[J]. Acta materialia, 2003, 51(19): 5775-5799. DOI:10.1016/j.actamat.2003.08.023 |
| [5] |
JING Z, CHEN B, ZHANG B. Effect of initial microstructure on the hot compression deformation behavior of a 2219 aluminum alloy[J]. Materials & Design, 2012, 34: 15-21. |
| [6] |
BEER A G, BARNETT M R. Influence of initial microstructure on the hot working flow stress of Mg-3Al-1Zn[J]. Materials Science and Engineering: A, 2006, 423(1-2): 292-299. DOI:10.1016/j.msea.2006.02.041 |
| [7] |
ZHENG J, LIU H, REN Y, et al. Effect of two-dimensional ultrasonic rolling on grain size and micro-hardness of 7075 aluminum alloy[J]. International Journal of Advanced Manufacturing Technology, 2020, 106(9-12): 1-8. |
| [8] |
ROKNI M R, ZAREI-HANZAKI A, ROOSTAEI ALI A, et al. An investigation into the hot deformation characteristics of 7075 aluminum alloy[J]. Mater Des, 2012, 34: 15-21. DOI:10.1016/j.matdes.2011.07.061 |
| [9] |
CAVALIERE P, SQUILLACE A. High temperature deformation of friction stir processed 7075 aluminium alloy[J]. Materials Characterization, 2005, 55(2): 136-142. DOI:10.1016/j.matchar.2005.04.007 |
| [10] |
GOURDET S, MONTHEILLET F. A model of continuous dynamic recrystallization-ScienceDirect[J]. Acta Materialia, 2003, 51(9): 2685-2699. DOI:10.1016/S1359-6454(03)00078-8 |
| [11] |
TANG B, LI H, GUO N, et al. Revealing ductile/quasi-cleavage fracture and DRX-affected grain size evolution of AA7075 alloy during hot stamping process[J]. International Journal of Mechanical Sciences, 2021, 212: 106843. DOI:10.1016/j.ijmecsci.2021.106843 |
| [12] |
章海明, 徐帅, 李倩, 等. 晶体塑性理论及模拟研究进展[J]. 塑性工程学报, 2020, 27(5): 12-32. |
| [13] |
KALIDINDI S R, BRONKHROST C A, ANAND L. Crystallographic texture evolution in bulk deformation processing of FCC metals[J]. Journal of the Mechanics & Physics of Solids, 1992, 40(3): 537-569. |
| [14] |
LIU G, MO H, WANG J, et al. Coupled crystal plasticity finite element-phase field model with kinetics-controlled twinning mechanism for hexagonal metals[J]. Acta Materialia, 2021, 202(1-2): 399-416. |
| [15] |
ROTERS F, RAABE D, GOTTSTEIN G., et al. Work hardening in heterogeneous alloys-a microstructural approach based on three internal state variables[J]. Acta Materialia, 2000, 48(17): 4181-4189. DOI:10.1016/S1359-6454(00)00289-5 |
| [16] |
HANAMURA T, TORIZUKA S, TAMURAS, et al. Effect of austenite grain size on the mechanical properties in air-cooled 0.1C-5Mn martensitic steel[J]. Materials Science Forum, 2014, 783-786: 1027-1032. DOI:10.4028/www.scientific.net/MSF.783-786.1027 |
| [17] |
SHANG X, ZHANG H, CUI Z, et al. A multiscale investigation into the effect of grain size on void evolution and ductile fracture: Experiments and crystal plasticity modeling[J]. International Journal of Plasticity, 2020, 125: 133-149. DOI:10.1016/j.ijplas.2019.09.009 |
| [18] |
MA A, F ROTERS, D RAABE. A dislocation density based constitutive model for crystal plasticity FEM including geometrically necessary dislocations[J]. Acta Materialia, 2006, 54(8): 2169-2179. DOI:10.1016/j.actamat.2006.01.005 |
| [19] |
QUEYREAU S, MONNE G, DEVINCRE B. Slip systems interactions in α-iron determined by dislocation dynamics simulations[J]. International Journal of Plasticity, 2009, 25(2): 361-377. DOI:10.1016/j.ijplas.2007.12.009 |
| [20] |
BGNA, B J S, P E J. Rivera-díaz-del-castillo a. dislocation annihilation in plastic deformation: Ⅱ. Kocks-Mecking analysis[J]. Acta Materialia, 2012, 60(6-7): 2615-2624. DOI:10.1016/j.actamat.2012.01.028 |
| [21] |
MECKING H, KOCKS U F. Kinetics of flow and strain-hardening[J]. Acta Metallurgica, 1981, 29(11): 1865-1875. DOI:10.1016/0001-6160(81)90112-7 |
 2023, Vol. 37
2023, Vol. 37


