| 基于卷积网络的OFDM系统信道解码技术 |
2. 山东大学 信息科学与工程学院, 山东 青岛 266237;
3. 山东正晨科技股份有限公司, 山东 济南 250101
2. School of Information Science and Engineering, Shandong University, Qingdao 266237, China;
3. Shandong Zhengchen Technology Co.Ltd, Jinan 250101, China
无论对于单载波还是多载波传输方案, 接收端采用相干解调恢复数据信息时, 都需要较为准确的信道状态信息(channel statistic information, CSI)作为数据处理的必要参数。所以, 信道估计技术对于无线通信有着重要的作用[1]。信道估计技术是从接收信号中估计出移动信道的特性, 可以估计信道的冲激响应, 也可以估计出其频率特性。通常对信道估计技术的评价有三方面: 对数据传输效率的影响、计算的复杂度以及估计的准确程度。一般对于信道估计技术, 我们希望其能在低复杂度的同时尽量提高系统估计的准确度。
OFDM技术是一种特殊的多载波传输方案[2], 它可以被看作一种调制技术, 是一种当前应用广泛的多载波技术。对于OFDM系统的信号恢复, 需要较为准确的CSI作为依照, 例如LS算法以及MMSE算法等传统的信道估计算法。其中, LS方法使测量值和模型之间的加权误差最小, 对于慢衰落信道, CSI在几个符号时间内不会发生改变, 可以直接采用LS法求得[3]。而对于其他衰落信道, 可通过采用梳状导频方式进行信道估计, 导频处的CSI采用LS法求得, 数据处的CSI通过内插得到, 但LS方法容易受到高斯噪声和载波间干扰的影响。MMSE方法在相同的均方误差下, 与LS法相比, 有10~15 dB的信噪比增益, 由于涉及到大规模的矩阵求逆, 复杂度随观察采样数目呈指数增长, 虽然可以通过对发射数据取平均来减少复杂度, 但复杂度较高还是限制了该方法的大规模应用[4]。此外还有基于DFT的信道估计技术, 该技术通过消除最大时延外的噪声, 改善了传统LS或MMSE技术的性能[5]。
近些年, 人工智能技术在自然语言处理、语音识别等方面获得了巨大成功[6], 同时近些年也应用在军事、社会生活方面[7-9]。经典的网络有深度神经网络(deep neural network, DNN)、循环神经网络(recurrent neural network, RNN)、生成对抗神经网络(generative adversarial network, GAN)和CNN[10]等。近些年, 研究逐渐将信号处理与神经网络结合, 其中分为两类, 一类为数据驱动, 另外一类为模型驱动。文献[11]采用五层DNN网络DNet以端到端方式处理无线OFDM信号, 将接收信号作为输入, 原始信号作为标签输入神经网络, 使网络学习到信号之间的映射关系, 但输出信号准确性会随着输出个数增加而降低, 且需要8个相同结构的网络才能得到完整信号, 复杂度较高。但是作为较早地将信号处理与神经网络结合起来的成果, 它仍然对我们的工作有着较大的启发。首先, 我们通过对其成果进行复现, 了解了设计背后的逻辑, 启发了我们设计性能更加优越、结构更加完善、使用范围更广的网络。其次, 通过使用结构更加复杂的网络, 例如长短期记忆网络, 设计能够更好更快地完成信号处理各项任务。文献[12]通过利用DNNs完成通信中编码、解码、调制和均衡功能, 利用GAN得到信道CSI。文献[13]采用CNNs和FC层完成OFDM系统FFT、解调、信道估计的功能模块。文献[14]采用模型驱动与数据驱动的方法, 设计ComNet接收机网络结构, 即传统LS估计、ZF均衡算法与神经网络相结合的方法, 提高了算法的准确性。显然, 结合发展成熟的传统算法, 凭借神经网络的优越的数据处理能力, 设计可以取得优越的性能。所述研究证明了近些年将深度学习与无线通信具体问题相结合的热潮, 通过大量的仿真实验, 证明了研究方向的可行性。因此, 在启发下, 提出了基于二维图片处理工具, 即卷积神经网络的信道解码网络。
设计采用数据驱动网络结构, 进行原始信号的检测, 通过设计的硬判决器进行信号判决, 考虑到梯度消失导致性能较差的现象, 引入了残差网络(residual network, RN)的残差连接(skip connected, SC)方式。通过实验仿真, 该设计在计算与系统复杂度上有着较大的优势, 为信号处理技术的发展与革新提供参考。
1 OFDM系统结构图 1是多径和AWGN影响下的传统OFDM收发机系统结构图, 采用传统通信环境进行设计可行性的验证。采用的具体参数见表 1。
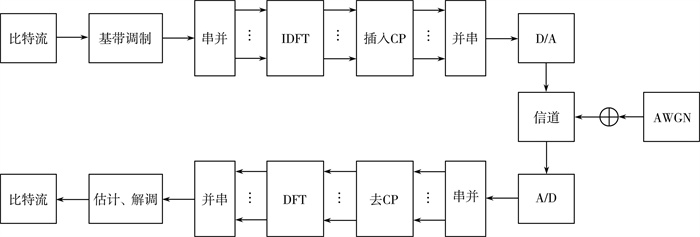 |
| 图 1 OFDM通信系统 |
| 表 1 系统主要参数 |
 |
图 2为仿真信号结构图, 一帧包含一个OFDM符号, 即信道在一个OFDM信号内是不变的, 其中数据子载波数目为64。设计思想是在线下训练时发送数帧的训练序列, 训练网络学习到信号之间的映射方式。
 |
| 图 2 OFDM帧结构 |
对于在线估计阶段, 包含了64个数据子载波的OFDM符号, 由于不包含导频开销, 从而提高了传输效率。
多径信道的冲激响应用hi, j(τk, t)来描述, 公式为
| $ h_{i, j}\left(\tau_{k}, t\right)=(1 / \sqrt{M}) \sum\limits_{k=1}^{L}[k] \sum\limits_{l=1}^{M} \mathrm{e}^{j\left(2 \pi f_{i, j, k, l^{t}}+\theta_{i, j, k, l}\right)} \cdot \delta\left(\tau-\tau_{k}\right), $ | (1) |
| $ f_{i, j, k, l}=f_{d, \max } \sin \left(2 \pi u_{i, j, k, l}\right) 。$ | (2) |
式(1)中θi, j, k, l=2πui, j, k, l为离散多普勒相位; ui, j, k, l为独立随机变量; L为多径信道的径数; M为调和系数。式(2)中, fi, j, k, l为离散多普勒频移; fd, max为最大多普勒频移。
待传输的比特信息经过QPSK调制后串并变换, 利用快速傅里叶逆变换(invert fast fourier transform, IFFT)实现发送端信号上变频, 然后插入循环前缀(cyclic prefix, CP), 目的是消除符号间干扰(inter symbol interference, ISI), 此时待发送信号可以表示为
| $ s(t)=\left\{\sum\limits_{i=0}^{N-1} d_{i} \exp \left[j 2 \pi \frac{i}{T}\left(t-t_{s}\right)\right]\right\} \operatorname{rect}\left(t-t_{s}-\frac{T}{2}\right)_{\circ} $ | (3) |
式(3)中di为分配给每个子信道的数据符号; ts为一个OFDM符号的时间起点; T为OFDM符号周期; N为子载波数。
发送信号经过信道, 接收信号表示为
| $ Y(k)=X(k) \cdot H(k)+N(k) 。$ | (4) |
式(4)中Y(k)为第k个子载波接收信号; X(k)为频域发送信号; H(k)为信道频域响应; N(k)为子载波的高斯噪声。
2 基于数据驱动的信道解码本节主要设计了一种基于深度学习的信道解码方法(decoding net, DCNet), 将接收信号看作一维数组, 利用CNNs进行特征提取, 降低了信号操作的复杂度, 相较于DNet, 减少了神经网络训练参数, 优化了结构性能, 避免了文献11中的性能临界的缺点, 接着设计了两层FC层分类、输出。设计提出的信道解码的方法, 通过大规模的数据训练, 可以实时追踪信号的变化, 相较于其他方法, 训练时间短, 性能有提升。
2.1 DCNet结构设计采用的信道解码结构分为线下训练与在线估计两部分, 线下训练完成后可代替原OFDM系统的若干功能模块, 结构图如图 3所示。
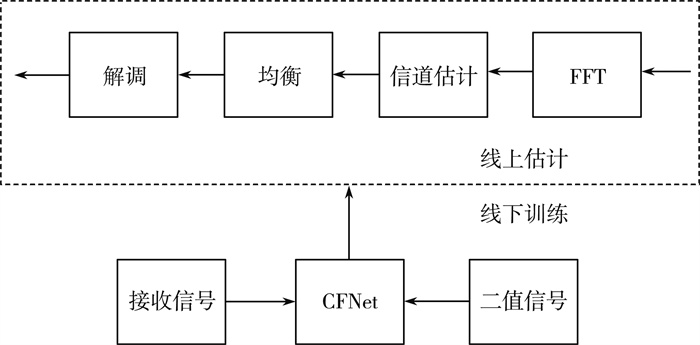 |
| 图 3 信道估计与均衡部分 |
由图 3可知, 结构分为两部分, 即线下训练与线上估计。在线下训练阶段, 利用发射机发送数帧先验信号训练神经网络, 以经过信道, 去除CP的接收信号作为神经网络的输入, 原始信号(hard bits, HB)作为标签训练神经网络。DCNet网络由CNN和DNN组成, 其中包含三层CNN网络, 用于接收信号的特征提取, 其中每一层包括卷积操作, 批次归一化(batch normalization, BN)和激活操作, FC层包含一层隐藏层, 个数为512, 激活函数为线性整流函数(rectified linear unit, ReLU), 最后一层为输出层, 个数为128, 激活函数为逻辑函数(sigmoid), 网络结构见图 4。
 |
| 图 4 DCNet结构 |
同时为了解决可能出现的梯度消失的现象, 采用了RN网络的SC方式, 输出为数个状态的叠加, 一般结构见图 5。
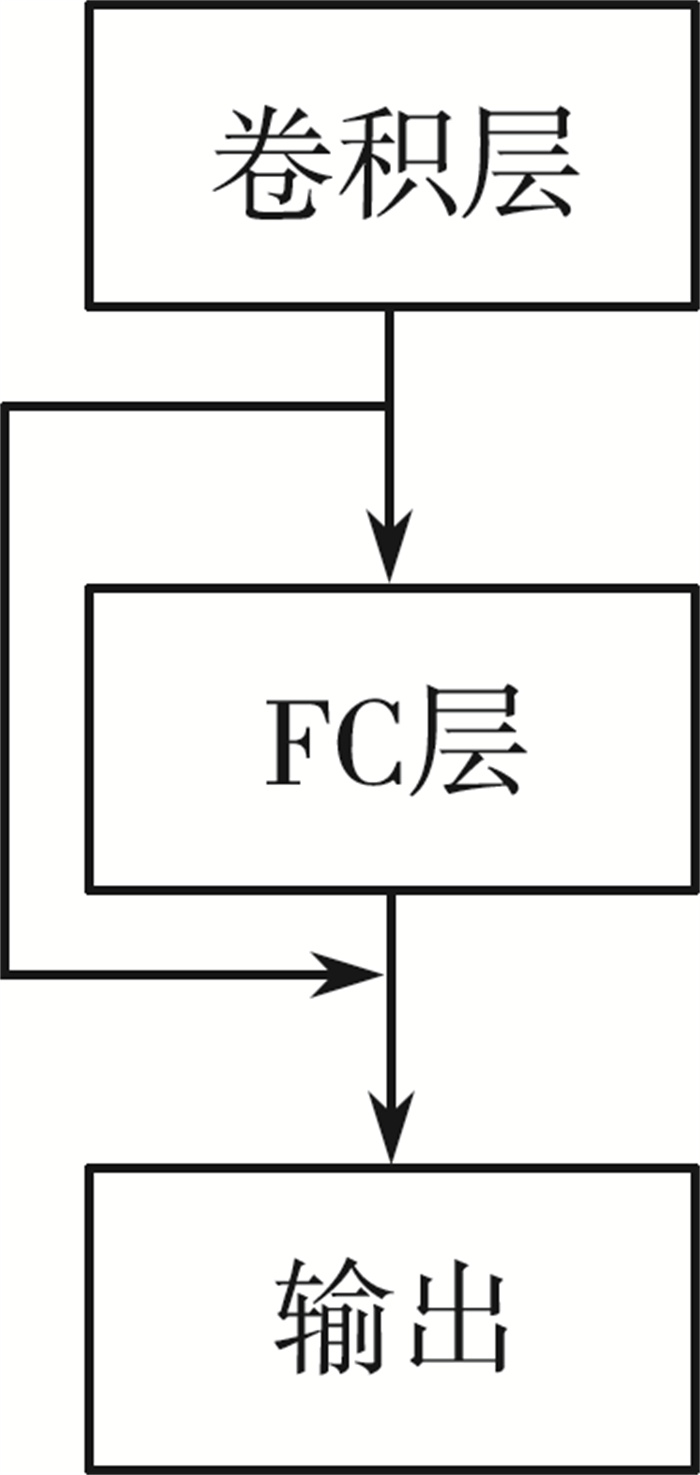 |
| 图 5 残差连接的一般形式 |
由图 5可知, 输出可以表示为输入和输入的数个非线性变换的线性叠加, 它解决了深层网络的训练问题。
假设前向传播过程为
| $ f^{\prime}=f(x, w), $ | (5) |
| $ g^{\prime}=g\left(f^{\prime}\right), $ | (6) |
| $ y^{\prime}=k\left(g^{\prime}\right), $ | (7) |
| $ loss =\operatorname{MSE}\left(y, y^{\prime}\right) 。$ | (8) |
式(5)中f为卷积操作; 式(6)中g为激活函数; 式(7)中k为分类器; 式(8)中 MSE 为均方误差操作, 公式为
| $ L\left(y^{\prime}, y\right)=|| y^{\prime}-y||^{2}=\sum\limits_{i=1}^{k}\left[y^{'(i)}-y^{(i)}\right]^{2} , $ | (9) |
式(9)中o(m)为预测值; y为真实值。反向传播过程公式为
| $ \partial loss / \partial w=\left(\partial loss / \partial y^{\prime}\right)\left(\partial y^{\prime} / \partial g^{\prime}\right)\left(\partial g^{\prime} / \partial f^{\prime}\right)\left(\partial f^{\prime} / \partial w\right) 。$ | (10) |
由式(10)可得, 一旦其中某个参数很小, 多次连乘后梯度会越来越小, 影响性能, 使用残差连接后, 反向传播过程变为
| $ (\partial h / \partial x)=((\partial f+x) / \partial x)=(\partial f / \partial x)+1 。$ | (11) |
式(11)相当于每一个导数加1, 此时梯度便不会出现消失的现象。
图 6为简化的系统解码过程, 是一种端到端的信号处理方式, 将接收信号作为网络输入, 通过卷积网络进行特征提取, 通过FC层分类, 输出SB信号, 最后通过设计的判决方式进行信号判决, 得到原始信号。
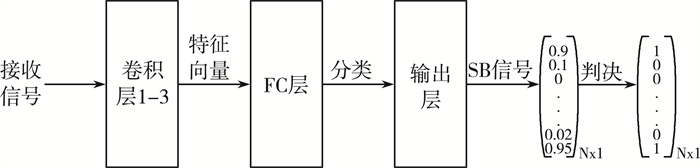 |
| 图 6 系统解码过程 |
由上图可知, 对于二分类层输出的离散信号, 作为一种概率类信号, 在做判决时需要通过测量欧式距离来确定输出的原始比特信号。
2.2 模型训练由于实际的CSI难以得到, 设计数据由仿真模拟生成, 其中神经网络的搭建与训练采用TensorFlow库, 网络参数见表 2。
| 表 2 DCNet参数 |
 |
由表 2可知, 网络输入为一组OFDM符号的形式, 经过数个卷积和BN过程后, 通过FC层输出一个OFDM符号的SB信号, 完成信道估计过程, 再经过接收端的信号处理, 消除信号的失真, 还原原始信号。
2.3 训练过程与DNet相比, 设计在训练过程中采用了一些方法优化训练过程, 采用了BN操作, 消除过拟合现象, 该方法首次由Google在2015年提出, 按照一般的神经网络训练过程, 通常是在每层网络激活后进行归一化操作, 但在文献[15]中, 提出了在激活之前进行归一化操作, 因为在训练初期, 分界面变化剧烈, 计算的参数不稳定, 而且初始的权重是在标准高斯分布中采样得到的, 数值较大, 因此在激活之前进行BN操作可以得到更稳定的结果, 对于每一个输入, 进行以下变换
| $ \hat{x}=(x-E[x]) / \sqrt{V[x]} 。$ | (12) |
公式(12)中
| $ y=\gamma \hat{x}+\beta \text { 。} $ | (13) |
BN操作基于小批量梯度下降算法, 式(13)是为了保证非线性的获得, 参数γ和β通过训练获得。
训练网络的学习率问题对于网络训练效率有着至关重要的影响, 设计采用反时限学习率衰减算法, 自动更新学习率, 公式为
| $ L=L_{\mathrm{i}} /\left(1+D_{\mathrm{r}} * s\right) 。$ | (14) |
公式(14)中L为当前学习率; Li为初始学习率; Dr为学习率衰减率; s为衰减频率。设计初始学习率为0.01, 衰减频率为200, 学习率衰减率为0.9。
2.4 判决由于设计采用的是等概率的单极性不归零码, 每个码元时间的中间点是采样点, 最佳判决门限公式
| $ \gamma=-\ln 3 / 2 A 。$ | (15) |
在式(15)中A为信号的幅值, 发送端信号集为H{0, 1}, 信道噪声为均值为0, 方差为σ2的高斯噪声, 则接收端信号Z(t)分别为两个高斯分布的信号, 均值分别为A和0, 方差为σ2。
3 仿真结果设计仿真环境为126G内存, Intel Core i9-9820X CPU, GeForce RTX 2080 Ti图形处理器, 编程环境为python3.7, tensorflow1.13.0, numpy1.18.5, 一次喂入1 000组接收信号, Batch size为10 000, 训练过程总耗时10 min。
图 7显示了DCNet、DNet中基于FC的神经网络和传统LS、MMSE算法的系统误码率(bit error rate, BER)曲线。通过对比, 证明了CNNs应用到通信系统信道解码技术的可行性, 性能在特定情形下有着一定的优越性。它展示了DCNet网络相较于FC网络在相同情况下有着至少2 dB性能的提升。以信噪比为14 dB时为例, DCNet设计的BER已经达到0.01, 相较于传统MMSE算法, 性能提升了4 dB, 而对于LS法, 则提升巨大。
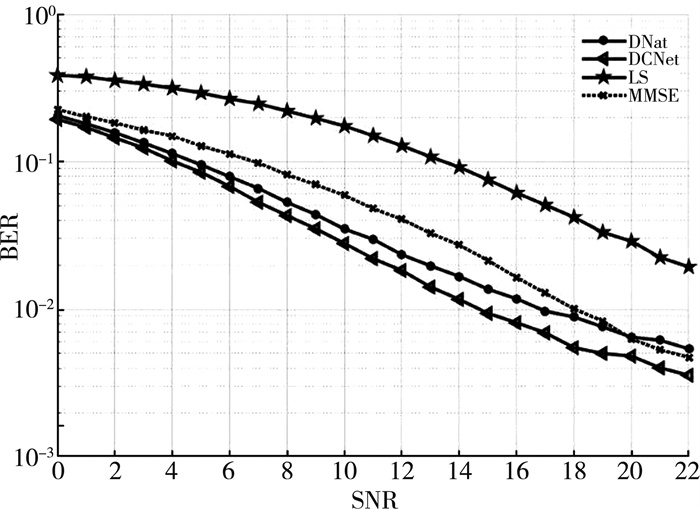 |
| 图 7 BER性能分析 |
图 8显示了不同SNR情形下的误差下降率(mean error rate, MER)曲线, 在低信噪比的情况下, DCNet网络能够大幅度降低MER, 这也同样显示了在固定信噪比训练下的影响。
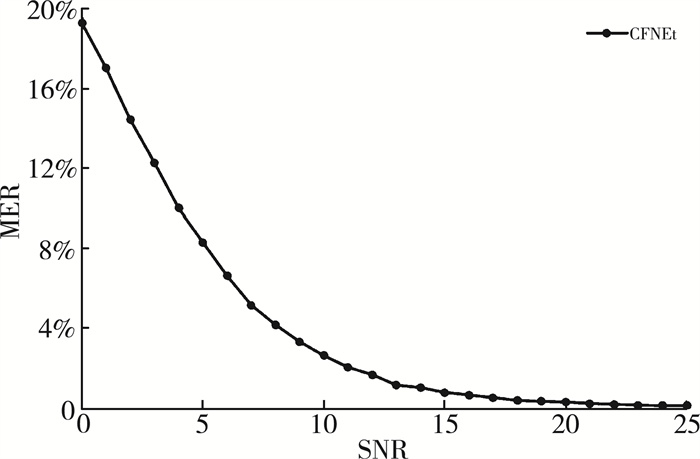 |
| 图 8 MER性能 |
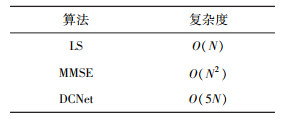
表 3为DCNet与LS、MMSE方法的复杂度分析。由表可知, MMSE算法复杂度会随着数据量出现二次增长, LS与DCNet算法复杂度会随着输入数据量的增长而线性增长, 其中LS法复杂度最低, DCNet次之, 这证明了该方法具有一定的可行性。
| 表 3 复杂度分析 |
 |
然而, 随着信噪比的增大, 传统方法的性能提升速度加快, DNet与DCNet等基于深度学习的设计则提升缓慢, 这一方面是由于传统方法在干扰少的通信环境下的出色性能, 另一方面是设计训练基于固定信噪比, 即训练集范围小, 因此设计的泛化性能较差。
4 结论本文提出了一种基于残差连接CNN的OFDM系统信道解码技术, 通过利用高性能计算机, 构建数层的神经网络, 采用先进算法, 避免了梯度消失、耗时长等问题。实验结果表明, 训练得到的神经网络与采用了FC连接的论文方法相比有着一定的优越性, 与传统方法相比则性能提升较大, 具有一定的应用价值。但对于在高信噪比环境下的性能表现有着一定的不足, 这从侧面证明了数据集大小对于设计的影响。因此, 如何高效地收集准确数据并标记, 设计适用范围更广的网络将是我们下一步的工作。
| [1] |
李莉. MIMO-OFDM系统原理、应用及仿真[M]. 北京: 机械工业出版社, 2014: 89-94.
|
| [2] |
XU Y J, HU Y, CHEN Q B. Optimal power allocation for multiuserofdm-based cognitive heterogeneous networks[J]. China Communications, 2017, 14(9): 52-61. DOI:10.1109/CC.2017.8068764 |
| [3] |
LEE J, HAN J, KIM S. Joint carrier frequency synchronization and channel estimation for ofdm systems via the em algorithm[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 167-172. DOI:10.1109/TVT.2005.861212 |
| [4] |
DE BEEK JV, EDFORS O, SANDELL M. On channel estimation in ofdm systems[J]. IEEE 45th Vehicular Technology Conference, 1995, 2(6): 815-819. |
| [5] |
JEON C, GHODS R, MALEKI A, et al. Optimality of large mimo detection via approximate message passing[C]//2015 IEEE International Symposium on Information Theory (ISIT), Hong Kong, China: Chinese society of Electronics, 2015.
|
| [6] |
MAO Q, HU F, HAO Q. Deep learning for intelligent wireless networks: a comprehensive survey[J]. IEEE Communications Surveys and Tutorials, 2018, 20(4): 2595-2621. DOI:10.1109/COMST.2018.2846401 |
| [7] |
SUN Z Z, WANG L, WANG C G, et a. An adaptive transmission scheme for deep space communication[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2019, 36(1): 26-35. |
| [8] |
WANG C Q, XIAO Z L, ZHANG Q. Advantage competition of air and space in artificial intelligence era[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2020, 37(4): 501-507. |
| [9] |
LI N, JIAO Q Y, ZHU X H. Prediction of departure aircraft taxi time based on deep learning[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2020, 37(2): 232-241. |
| [10] |
张静, 金石, 温朝凯. 基于人工智能的无线传输技术最新研究进展[J]. 电信科学, 2018, 34(8): 46-55. |
| [11] |
YE H, LI G Y, JUANG B H. Power of deep learning for channel estimation and signal detection in ofdm systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114-117. DOI:10.1109/LWC.2017.2757490 |
| [12] |
YE H, LI G Y, JUANG B F, et al. Channel agnostic end-to-end learning based communication systems with conditional gan[C]// 2018 IEEE Globecom Workshops (GC'18 Workshops), Dubai: United Arab Emirates, 2018.
|
| [13] |
ZHAO Z, VURAN M C, GUO F. Deep-waveform: a learned ofdm receiver based on deep complex-valued convolutional networks[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(8): 2407-2420. DOI:10.1109/JSAC.2021.3087241 |
| [14] |
HE H, JIN S, WEN C. Model-driven deep learning for physical layer communications[J]. IEEE Wireless Communications, 2019, 26(5): 77-83. DOI:10.1109/MWC.2019.1800447 |
| [15] |
WU S, LI G Q, DENG L. L1-norm batch normalization for efficient training of deep neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(7): 2043-2051. DOI:10.1109/TNNLS.2018.2876179 |
 2022, Vol. 36
2022, Vol. 36

