期权交易出现以后, 作为期权交易核心部分的期权定价一直深受金融数学的重视。究其原因, 期权定价具有两方面卓越的优势^[1]: 一方面, 期权定价模型能够帮助公司模拟债务的最优定价；另一方面, 期权定价模型可以对各类具有风险信息的产品进行风险评估。正是由于这两个独特的优势, 使得期权模型可以广泛应用于风险的量化以及定价的最优化设计。自2001年以来, 国内开始选取Black-Scholes期权价格模型进行研究, 研究多采用实证分析法, 此后国内外研究多使用极大似然估计进行数值分析模拟求解且不断完善数据, 从而减小Black-Scholes期权模型的误差^[2]；同时也有学者对于Black-Scholes期权模型提出修正^[3], 从而减小误差, 提升准确性。随着金融市场的不断发展, 传统的Black-Scholes期权模型的缺点日益凸显, 2016年, Ivancevic把非线性薛定谔方程拟合传统的Black-Scholes期权模型^[4], 引入了非线性的期权价格模型, 使得对于期权定价模型的研究步入了新台阶。目前研究的重点在于使用不同方法对期权定价模型求解, 进一步让其能够投入应用, 并继续扩展。本文选取Ivancevic期权模型, 使用双线性方法^[5], 引入D-算子, 利用D-算子和摄动法, 求解双线性方程, 从而获得精确解。并绘制精确解与相关系数之间的图像, 分析不同系数对于期权定价的意义, 为期权模型的应用提供一定参考价值。

1 Ivancevic期权模型的引入

传统的Black-Scholes期权定价模型^[6]方程如下

$ \frac{\partial u}{\partial t}+r s \frac{\partial u}{\partial s}+\frac{s^2 \sigma^2 \partial^2 u}{\partial s^2}-r u=0, $

(1)

非线性薛定谔方程^[7]如下

$ i \frac{\partial u}{\partial t}+\frac{1}{2} \frac{\partial^2 u}{\partial s^2}+|u|^2 u=0。$

(2)

2016年, 澳大利亚研究员Vladimir G.Ivancevic^[4]在非线性薛定谔方程的基础上拟合Black-sholes期权定价模型, 提出了Ivancevic期权定价模型

$ i \frac{\partial u}{\partial t}+\frac{1}{2} \sigma \frac{\partial^2 u}{\partial s^2}+\beta|u|^2 u=0, $

(3)

其中, i为虚数, u为期权的价格波函数, s为股票价格, t为执行时间, σ为波动率, β为自适应的市场潜力。

2 对Ivancevic期权定价模型求解

双线性导数定义^[8]

设f, g是变量t, x的可微函数, 引进微分算子D, D使得对任意的非负整数m, n有

$ D_t^m D_x^n f \cdot g=\left.\left(\partial_t-\partial_{t^{\prime}}\right)^m\left(\partial_x-\partial_{x^{\prime}}\right)^n f(t, x) g\left(t^{\prime}, x^{\prime}\right)\right|_{t^{\prime}=t, x^{\prime}=x}, $

(4)

称为函数f与g对t施行m次D_t, 对x施行n次D_x的双线性导数。

由定义可得双线性微分算子具有如下性质^[9]

$ D_t g \cdot f=g_t f-g f_t, $

(5)

$ D_s^2 g \cdot f=g_{s s} f-2 g_s f_s+f_{s s} g。$

(6)

设方程(3)解可表示分式$u=\frac{g(t, s)}{f(t, s)}$, 其中f(t, s)为实函数, g(t, s)为复函数, 将其代入(3)后得到

$ i\left(\frac{g}{f}\right)_t+\frac{1}{2} \sigma\left(\frac{g}{f}\right)_{s s}+\beta\left|\frac{g}{f}\right|^2 \frac{g}{f}=0, $

(7)

借助双线性微分算子性质(5), (6)可将方程(7)写成如下形式

$ \frac{i D_t g \cdot f}{f^2}+\frac{1}{2} \sigma\left(\frac{D_s^2 g \cdot f}{f^2}-\frac{g}{f} \frac{D_s^2 f \cdot f}{f^2}\right)+\beta\left|\frac{g}{f}\right|^2\left|\frac{g}{f}\right|=0, $

(8)

化简整理化为双线性形式为

$ \left(i D_t+\frac{1}{2} \sigma D_s^2\right) g \cdot f=0, $

(9)

$ \frac{1}{2} \sigma D_s^2 f f=\beta g g^*。$

(10)

若f可按参数ε的偶次幂展成级数, g按参数ε的奇次幂展成级数

$ f(t, s)=1+f^{(2)} \varepsilon^2+f^{(4)} \varepsilon^4+\cdots+f^{(2 j)} \varepsilon^{2 j}+\cdots, $

(11)

$ g(t, s)=g^{(1)} \varepsilon+g^{(3)} \varepsilon^3+\cdots+g^{(2 k+1)} \varepsilon^{2 k+1}+\cdots, $

(12)

$ \varepsilon:\left(i D_t+\frac{1}{2} \sigma D_s^2\right) g \cdot f=0, $

(13)

$ \varepsilon^2: \frac{1}{2} \sigma D_s^2\left(f^{(2)} \cdot 1+1 \cdot f^{(2)}\right)=\beta g^{(1)} g^{(1) *}, $

(14)

$ \varepsilon^3:\left(i D_t+\frac{1}{2} \sigma D_s^2\right)\left(g^{(3)} \cdot 1+1 \cdot g^{(3)}+g^{(1)} \cdot f^{(2)}+f^{(2)} \cdot g^{(1)}\right)=0, $

(15)

$ \varepsilon^4: \frac{1}{2} \sigma D_s^2\left(f^{(4)} \cdot 1+f^{(2)} \cdot f^{(2)}+1 \cdot f^{(4)}\right)=\beta\left(g^{(1)} g^{(3) *}+g^{(3)} g^{(1) *}\right), $

(16)

$ \varepsilon^5:\left(i D_t+\frac{1}{2} \sigma D_s^2\right)\left(g^{(5)} \cdot 1+1 \cdot g^{(5)}+g^{(1)} \cdot f^{(4)}+f^{(4)} \cdot g^{(1)}+g^{(3)} \cdot f^{(2)}+f^{(2)} \cdot g^{(3)}\right)=0, $

(17)

$ \varepsilon^6: \frac{1}{2} \sigma D_s^2\left(f^{(6)} \cdot 1+f^{(2)} \cdot f^{(4)}+f^{(4)} \cdot f^{(2)}+1 \cdot f^{(6)}\right)=\beta\left(g^{(1)} g^{(5)}{ }^*+g^{(5)} g^{(1) *}+g^{(3)} g^{(3)}{ }^*\right), $

(18)

整理ε同次幂系数得

$ i g_t^{(1)}+\frac{1}{2} \sigma g_{s s}^{(1)}=0, $

(19)

$ \sigma f_{s s}^{(2)}=\beta g^{(1)} g^{(1) *}, $

(20)

$ i g_t^{(3)}+\frac{1}{2} \sigma g_{s s}^{(3)}=-\left(i D_t+\frac{1}{2} \sigma D_s^2\right) g^{(1)} \cdot f^{(2)}, $

(21)

$ \sigma f_{s s}^{(4)}=-\frac{1}{2} \sigma D_s^2 f^{(2)} \cdot f^{(2)}+\beta\left(g^{(1)} g^{(3) *}+g^{(3)} g^{(1)^*}\right), $

(22)

$ i g_t^{(5)}+\frac{1}{2} \sigma g_{s s}^{(5)}=-\left(i D_t+\frac{1}{2} \sigma D_s^2\right)\left(g^{(1)} \cdot f^{(4)}+g^{(3)} \cdot f^{(2)}\right), $

(23)

$ \begin{gathered} \sigma f_{s s}^{(6)}=-\sigma D_s^2 f^{(2)} \cdot f^{(4)}+\beta\left(g^{(1)} g^{(5)^*}+g^{(3)} g^{(3)^*}+g^{(5)} g^{(1)^*}\right), \\ \ldots \end{gathered} $

(24)

由式(19)可取

$ g^{(1)}=\mathrm{e}^{\xi_1}, $

(25)

$ \xi_1=\omega_1 t+k_1 s+\xi_1^{(0)} \text { 其中 } \omega_1=i \frac{1}{2} \sigma k_1^2, $

(26)

代入式(20)解得

$ f^{(2)}=\mathrm{e}^{\xi_1+\xi_1^*+\theta_{13}}, $

(27)

$ \mathrm{e}^{\theta_{13}}=\frac{\beta}{\sigma\left(k_1+k_1^*\right)^2}, $

(28)

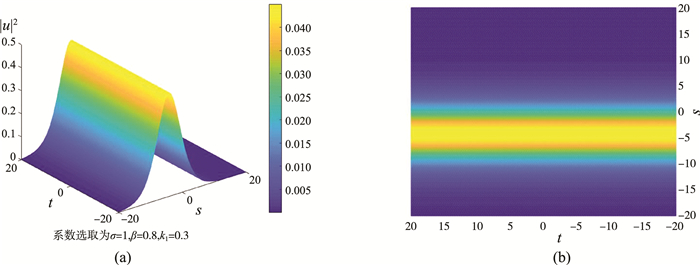
再取g⁽³⁾=f⁽⁴⁾=…=0如此可推知级数(19), (20)在当ε=1时截断为有限形式, 其单孤子解为

$ u=\frac{\mathrm{e}^{\xi_1}}{1+\mathrm{e}^{\xi_1+\xi_1^*+\theta_{13}}}, $

(29)

式(29)即为非线性薛定谔方程的单孤子解。同时得到|u|²的图像, 如图 1所示。

因为式(21)为线性齐次方程, 故也可取

$ g^{(1)}=\mathrm{e}^{\xi_1}+\mathrm{e}^{\xi_2}, $

(30)

$ \xi_j=\omega_j t+k_j s+\xi_j^{(0)} \text { 其中 } \omega_j=i \frac{1}{2} \sigma k_j^2, $

(31)

可得

$ f^{(2)}=\mathrm{e}^{\xi_1+\xi_1^*+\theta_{13}}+\mathrm{e}^{\xi_1+\xi_2^*+\theta_{23}}+\mathrm{e}^{\xi_2+\xi_1^*+\theta_{23}}+\mathrm{e}^{\xi_2+\xi_2^*+\theta_{24}}, $

(32)

$ \mathrm{e}^{\theta_{j, 2+l}}=\frac{\beta}{\sigma\left(k_j+k_l^*\right)^2}, (j, l=1, 2)。$

(33)

由式(21)解得

$ g^{(3)}=\mathrm{e}^{\xi_1+\xi_2+\xi_1^*+\theta_{12}+\theta_{13}+\theta_{23}}+\mathrm{e}^{\xi_1+\xi_2+\xi_2^*+\theta_{12}+\theta_{14}+\theta_{24}}, $

(34)

$ \mathrm{e}^{\theta_{12}}=-\frac{\frac{i\left(\omega_1-\omega_2-\omega_1^*\right)+\frac{1}{2} \sigma\left(k_1-k_2-k_1^*\right)^2}{\mathrm{e}^{\theta_{13}}}+\frac{i\left(\omega_2-\omega_1-\omega_1^*\right)+\frac{1}{2} \sigma\left(k_2-k_1-k_1^*\right)^2}{\mathrm{e}^{\theta_{23}}}}{i\left(\omega_1+\omega_2+\omega_1^*\right)+\frac{1}{2} \sigma\left(k_1+k_2+k_1^*\right)^2}, $

(35)

$ \mathrm{e}^{\theta_{34}}=\mathrm{e}^{\theta_{12}^*}。$

(36)

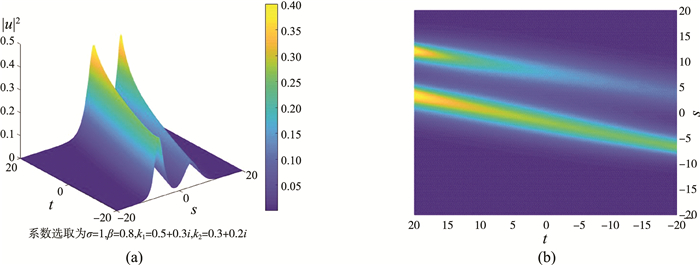
取g⁽⁵⁾=f⁽⁶⁾=…=0的截断式当ε=1可得

$ f_2(t, s)=1+\mathrm{e}^{\xi_1+\xi_1^*+\theta_{13}}+\mathrm{e}^{\xi_1+\xi_2^*+\theta_{23}}+\mathrm{e}^{\xi_2+\xi_1^*+\theta_{23}}+\mathrm{e}^{\xi_2+\xi_2^*+\theta_{24}}+\mathrm{e}^{\xi_1+\xi_2+\xi_1^*+\xi_2^*+\theta_{12}+\theta_{13}+\theta_{14}+\theta_{23}+\theta_{24}+\theta_{34}}, $

(37)

$ g_2(t, s)=\mathrm{e}^{\xi_1}+\mathrm{e}^{\xi_2}+\mathrm{e}^{\xi_1+\xi_2+\xi_1^*+\theta_{12}+\theta_{13}+\theta_{23}}+\mathrm{e}^{\xi_1+\xi_2+\xi_2^*+\theta_{12}+\theta_{14}+\theta_{24}}, $

(38)

$ u_2=\frac{g_2(t, s)}{f_2(t, s)}, $

(39)

式(39)即为非线性薛定谔方程的双孤子解。同时得到|u|²的图像, 如图 2所示。

3 非线性期权模型解的分析

取式(29)单孤子解u的共轭函数u^*

$ u^*=\frac{\sigma\left(k_1^*+k_1\right)^2 \mathrm{e}^{\xi_1^*}}{\sigma\left(k_1^*+k_1\right)^2+\beta \mathrm{e}^{\xi_1^*+\xi_1}}, $

(40)

由|u|²=u·u^*可得

$ |u|^2=\frac{\sigma^2\left(k_1+k_1^*\right)^4 \mathrm{e}^{\xi_1^*+\xi_1}}{\sigma^2\left(k_1+k_1^*\right)^4+2 \sigma \beta\left(k_1+k_1^*\right)^2 \mathrm{e}^{\xi_1^*+\xi_1}+\beta^2 \mathrm{e}^{2\left(\xi_1+\xi_1^*\right)}}, $

(41)

对式(41)取倒数并整理系数可得

$ \frac{1}{|u|^2}=\frac{1}{\mathrm{e}^{\xi_1^*+\xi_1}}+\frac{2 \beta}{\sigma\left(k_1+k_1^*\right)^2}+\frac{\beta^2 \mathrm{e}^{\left(\xi_1+\xi_1^*\right)}}{\sigma^2\left(k_1+k_1^*\right)^4}, $

(42)

将式(26)代入得

$ \frac{1}{|u|^2}=\frac{1}{\mathrm{e}^{\frac{1}{2} i \sigma\left(k_1^2+k_1^{* 2}\right) t+\left(k_1+k_1^*\right) s}}+\frac{2 \beta}{\sigma\left(k_1+k_1^*\right)^2}+\frac{\beta^2 \mathrm{e}^{\frac{1}{2} \sigma\left(k_1^2+k_1^{* 2}\right) t+\left(k_1+k_1^*\right) s}}{\sigma^2\left(k_1+k_1^*\right)^4}。$

(43)

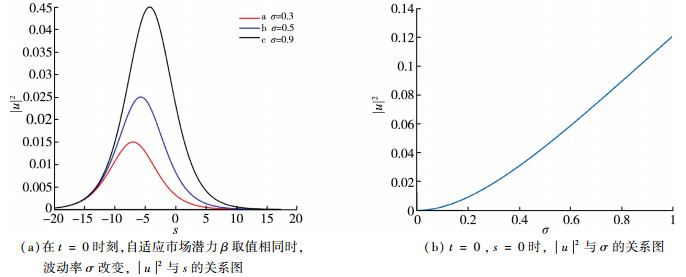
3.1 波动率对期权价格波函数的影响

波动率是期权定价理论中度量金融资产价格波动程度的一个统计参数。在式(43)中, 给定市场潜力β=0.8, 系数k₁=0.2保持不变, 在t=0时刻, 如图 3(a), 对于给定的波动率, 期权波函数随着股票价格s呈现波动趋势；而取定股票价格s=0, 时间t=0时, 如图 3(b), 当波动率σ增加, 在相同股票期权价格波函数|u|²值也会增加；从市场角度分析, 由于期权波动率σ增加, 期权上涨幅度也会增加, 反应到投资者, 其获利的概率也会增加。因此, 期权价格波函数|u|²的峰值会与波动率σ的增加成正比。

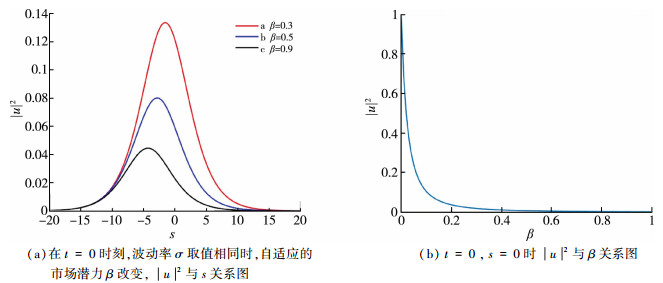
3.2 自适应市场潜力对期权价格波函数的影响

规定在简单的市场模型中, 自适应市场潜力β与无风险利率是相等的。式(43)中, 保持波动率σ=0.5, 系数k₁=0.2不变, 在t=0时刻, 由图 4(a)可得, 给定市场潜力β, 期权价格波函数|u|²值也与股票价格s呈波动趋势；而取定股票价格s=0, t=0, 由图 4(b), 从市场角度分析, 当市场潜力增加时, 买入期权的机会成本增加, 投资者更倾向将资本放入其他市场, 这会导致期权价格的降低。此行为反映到图像(b)中期权价格波函数|u|²峰值与市场潜力β增加成反比。

4 总结

本文使用双线性方法求解了Ivancevic所引入关于期权的非线性薛定谔模型, 给出了模型的单孤子解及其双孤子解, 绘制其模方函数图像, 同时研究波动率, 市场潜力对于期权价格波函数的影响, 分析到期时间对于获利的影响, 加快模型投入应用。