| 基于传染病模型的新冠肺炎传播问题研究 |
2. 齐鲁工业大学(山东省科学院)数学与统计学院,济南 250353
2. School of Mathematics and Statistics, Qilu University of Technology(Shandong Academy of Sciences), Jinan 250353, China
据世界卫生组织发布的统计数据[1], 截止2020年7月14日, 全球新冠肺炎累计确诊病例超过1 200万例, 累计死亡病例561 617例。目前, 全球215个国家和地区存在新冠肺炎确诊病例, 其中, 已有70个国家累计确诊病例超1万例;21个国家累计确诊超10万例;全球日新增病例数达到20万例。可见, 新冠疫情仍在全球持续蔓延, 并有不断加剧的趋势, 严重威胁人类安全, 冲击全球经济发展。
新冠肺炎在国内爆发后, 政府迅速采取全方位防控和治疗措施, 历尽数月终于在这场疫情阻击战中取得阶段性胜利, 作为人类命运共同体的一员积极主动向全球分享抗疫经验和成果。在全球疫情形势不断恶化下, 世界卫生组织呼吁各国加强一切预防和管控措施, 有效的防控措施将对疫情发展产生怎样的影响?本文将分阶段建立模型, 分析预防控制措施对疫情走势的影响, 以便为全球后续疫情控制提供理论依据。
1 模型介绍常见的传染病模型主要包括SI模型, SIS模型, SIR模型, SEIR模型[2], 利用微分方程建立不同类型传染病数学模型。模型中含有以下四类人群:
1) 易感者S:潜在的易感染人群;
2) 潜伏者E:已被感染但还未表现出来的人群;
3) 感染者I:确诊被感染的人群;
4) 康复者R:感染后被治愈的人群。
1.1 SI模型SI模型主要适用于艾滋病传染病中[2], 由于艾滋病有不可治愈性, 故该模型中不存在潜伏者E和康复者R这两类人群。假定总人口数N=S+I, 疾病流行期间考虑人口的出生率与自然死亡率分别为μ和ν, 暂不考虑因病死亡的人数, 且新增人数均为易感人群, 感染人数为βSI/N(β为一个正比例系数)。公式表达如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;S\left( {t + \mathit{\Delta }t} \right) - S\left( t \right) = \mu N\left( t \right)\mathit{\Delta }t - \beta \frac{{S\left( t \right)}}{N}\cdot\\ I\left( t \right)\mathit{\Delta }t - \nu S\left( t \right)\mathit{\Delta }t, \end{array} $ | (1) |
| $ \begin{array}{l} \;\;\;\;\;\;I\left( {t + \mathit{\Delta }t} \right) - I\left( t \right) = \beta \frac{{S\left( t \right)}}{N}\cdot I\left( t \right)\mathit{\Delta }t - \\ \nu I\left( t \right)\mathit{\Delta }t 。\end{array} $ | (2) |
当Δt→0时, 得微分方程组:
| $ \left\{ \begin{array}{l} \frac{{dS}}{{dt}} = \mu N - \frac{{\beta SI}}{N} - \nu S\\ \frac{{dI}}{{dt}} = \frac{{\beta SI}}{N} - \nu I \end{array} 。\right. $ | (3) |
在SI模型基础上, 将康复者转为易感人群比例设为α, SIS模型常用于流感[3], 考虑流感具有再发性, 康复者仍存在一定可能性转为易感人群。方程组表达式为:
| $ \left\{ \begin{array}{l} \frac{{dS}}{{dt}} = \mu N - \frac{{\beta SI}}{N} + \alpha I - \nu S\\ \frac{{dI}}{{dt}} = \frac{{\beta SI}}{N} - \alpha I - \nu I \end{array} 。\right. $ | (4) |
SIR模型中存在康复者R, 即在感染者中存在一定康复率使其成为康复者, 设康复率为γ。此模型常见于急性传染病模型[4], 发病迅速, 且感染治愈后体内含有抗体, 不会再成为易感者。方程组表达式为:
| $ \left\{ \begin{array}{l} \frac{{dS}}{{dt}} = \mu N - \frac{{\beta SI}}{N} - \nu S\\ \frac{{dI}}{{dt}} = \frac{{\beta SI}}{N} - \gamma I - \nu I\\ \frac{{dR}}{{dt}} = \gamma I - \nu R \end{array} 。\right. $ | (5) |
SEIR模型通常被用于带潜伏期的恶性传染病模型, 如麻疹, 天花, 狂犬病和SARS的传播[5], 此类模型治疗康复后体内含有抗体不再进行二次感染。
全部人口被分为易感人群S, 暴露人群E, 感染人群I, 康复人群R和死亡人群D, 且人口总数N=S+E+I+R+D。基于SIR模型, 潜伏者存在一定的确诊感染率, 记为δ, 流程图如图 1所示:
 |
| 图 1 SEIR模型的流程图 |
方程组如下:
| $ \left\{ \begin{array}{l} \frac{{dS}}{{dt}} = \mu N - \frac{{\beta SI}}{N} - \nu S\\ \frac{{dE}}{{dt}} = \frac{{\beta SI}}{N} - \delta E - \nu E\\ \frac{{dI}}{{dt}} = \delta E - \gamma I - \nu I\\ \frac{{dR}}{{dt}} = \gamma I - \nu R \end{array} 。\right. $ | (6) |
对上式方程组求解需要初始值S(0)、I(0)、E(0)及R(0), 以及参数δ, β, γ, ν, μ。
依据实战经验, 此次新冠肺炎具有14~21天不等的潜伏期[6], 对治愈之后的康复者体内虽会形成抗体, 但也存在二次感染的可能性。基于上述四种传染病模型的分析, 结合新冠肺炎的传染特点, SEIR模型是最适合的模型。
2 分阶段优化传染病模型以政府实行严防严控政策为变量, 将新冠肺炎发展过程分为以下三个阶段:
1) 控制前:此阶段接近于自然传播模式, 没有外界干预;
2) 控制中:人们开始意识到严控的重要性, 政府部门出台并实施严防严控;
3) 控制后:介入人为因素的控制传播模式。
本文主要建立控制前与控制后新冠肺炎传播模型, 有以下几方面的总体假设:
1) 假设新冠肺炎对该时间段人口自然出生率与死亡率无影响;
2) 将潜伏期定为ψ=14天[7];
3) 假设潜伏期人群不存在自愈情况;
4) 假设新冠肺炎康复者不存在二次患病的可能性;
5) 假设处于潜伏期且被隔离的人群不具有传染性;
6) 假设给出的数据足够有效。
2.1 控制前SEIR模型 2.1.1 控前模型假设1) 在传染病传播期间对应地区的总人数N视为常数;
2) 由易感者到最终患病需要直接接触的方式;
3) 患病者单位时间内接触的人数视为常数, 且接触时间足以使接触者患病;
4) 根据所得数据, 模型中存在四类人群:易感者S:健康者在人群中的比率;潜伏者E:潜伏者在人群中的比率;感染者I:感染者在人群中的比率;退出者R(包含“被治愈者”与“死亡者”):退出者在人群中的比率。
2.1.2 参数设定1) ξ—退出率:感染新冠肺炎患者日死亡率与康复率之和;
2) φ—每个患病者平均每天接触人数;
3) σ—潜伏者每日确诊率;
4) γ—地区流入及流出占该地总人口比率;
5) τ—流入人口中携带病毒的比率。
2.1.3 模型建立依据相关变量之间的关系以及传染病相关的传播规律, 由于人群均为易感人群, 所以新增人群模型中暂不考虑, 又将死亡率与康复率用退出率ξ表示, 进而建立控制前优化的SEIR模型:
| $ \left\{ \begin{array}{l} \frac{{dS\left( t \right)}}{{dt}} = - \varphi I\left( t \right)S\left( t \right)\\ \frac{{dE\left( t \right)}}{{dt}} = \varphi I\left( t \right)S\left( t \right) - \sigma E\left( t \right) + \gamma \tau - \gamma E\left( t \right)\\ \frac{{dI\left( t \right)}}{{dt}} = \sigma E\left( t \right) - \xi I\left( t \right)\\ \frac{{dR\left( t \right)}}{{dt}} = \xi I\left( t \right)\\ S({t_0}) = {S_0}, E({t_0}) = {E_0}, I({t_0}) = {I_0}, R({t_0}) = {R_0} \end{array} 。\right. $ | (7) |
对模型求解, 确定其相关参数即可求出相应结果:
1) ξ—对相应城市医疗水平以及统计数据进行分析, 可取其平均值;
2) φ—通过相关数据以及资料可得;
3) σ—由医学数据统计及疫情防控情况具体确定;
4) γ—官方数据查询可得;
5) τ—由医学以及交通部门发布的数据可得。
控前模型相应参数结果意义不大, 对于其具体数值便不再一一给出。
2.2 控制后SIR-YN模型 2.2.1 控后模型假设1) 采取对人员流动相应限制后, 不再考虑输入与输出人员对模型的影响;
2) 人口中的每个人都是易感人群;
3) 假设每个病人每天接触的人数为一个常数;
4) 疑似感染者入院治疗一经确诊就几乎完全隔离, 因此传播给他人的可能性极低;
5) 基于SIR模型增加两类人群:疑似者Y:疑似感染新冠病毒者在人群中的比率;未隔离者N:新冠肺炎患病者未隔离者的人数占总人口的比率, 即已确诊却未被有效隔离的人数在人群的比率。
2.2.2 参数设定补充1) κ—对疑似者每日内排除感染者的比率;
2) λ—对疑似者每日内确诊感染者的比率;
3) ω—未隔离者每日确诊为感染者的比率;
4) θ—未隔离者每日成为疑似者的比率;
5) ρ—患者每天接触人群比率。
且κ, λ, ω, θ, ρ∈(0, 1).
2.2.3 建立模型在SIR模型基础上添加相关参数, 在考虑疑似与未隔离人群的基础上, 给出相应流程图, 建立控制后SIR-YN模型,如图 2所示。
 |
| 图 2 控后SIR-YN模型流程图 |
| $ \left\{ \begin{array}{l} \frac{{dS\left( t \right)}}{{dt}} = \kappa Y\left( t \right) - \rho S\left( t \right)N\left( t \right)\\ \frac{{dI\left( t \right)}}{{dt}} = \omega N\left( t \right) - \xi I\left( t \right) + \lambda Y\left( t \right)\\ \frac{{dR\left( t \right)}}{{dt}} = \xi I\left( t \right)\\ \frac{{dY\left( t \right)}}{{dt}} = - \kappa Y\left( t \right) - \lambda Y\left( t \right) + \theta N\left( t \right)S\left( t \right)\\ \frac{{dN\left( t \right)}}{{dt}} = \left( {1 - \theta } \right)N\left( t \right)S\left( t \right) - \omega N\left( t \right)\\ S({t_0}) = {S_0}, I({t_0}) = {I_0}, R({t_0}) = {R_0}, Y({t_0}) = {Y_0}\\ \;\;\;\;\;N({t_0}) = {N_0} \end{array} 。\right. $ | (8) |
通过中国疾病预防控制中心官方网站收集某一具有代表性地区的完整真实数据, 对控制后SIR-YN模型中相关参数κ, λ, ω, θ, ξ, ρ具体数值进行求解, 并利用模型对疫情发展趋势进行相应预测。
1) 参数κ日排除率
κ=疑似人员每日排除人数/当日疑似人员总人数。
从中国疾病预防控制中心官方网站选取2月1日到3月11日每日排除人数与疑似总人数[8], 依据上式计算日排除率, 并对其进行3阶多项式拟合。
观察3阶拟合图 3, 疑似日排除率整体呈现上升趋势, 可见居家隔离等一系列政策的实施是有效的。2月份期间, 日排除率在3%附近波动, 在全国人民的全力奋战下疫情逐渐得到控制, 3月份的日排除率明显逐渐上升。日排除率趋势图中呈现两次波峰, 第一波峰出现在2月10日左右, 可能是由于医疗设备以及医护人员数量逐渐扩增等不稳定因素造成的;3月份之后, 又出现一次较大波峰, 这是由于医疗水平不断提高以及国际上关注度不断提升。通过上图进而确定参数κ日排除率在3%~10%之间, 则求出40天日排除率期的望值κ=5.7%。
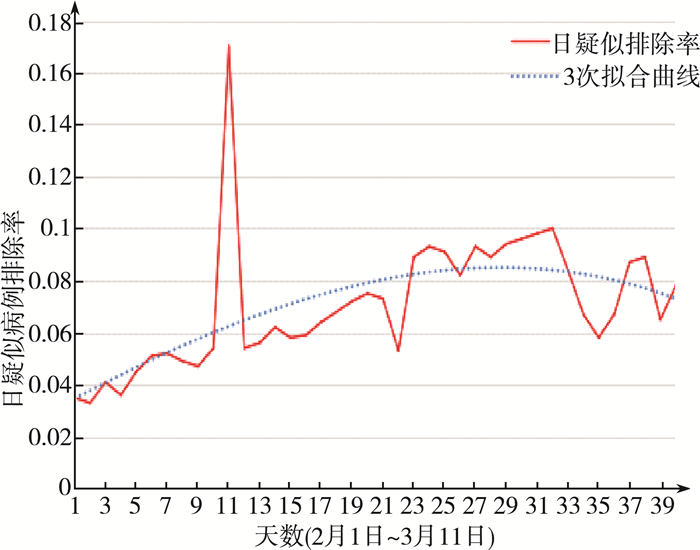 |
| 图 3 2月1日至3月11日疑似日排除率变化曲线图 |
2) 参数ξ日退出率
ξ=每日感染者中转为康复者以及死亡的总人数/当日确诊病例总数。
从中国疾病预防控制中心官方网站选取1月20日到3月30日每日康复人数、死亡人数和确诊病例总数[8], 依据上式计算日退出率, 并对其进行4阶多项式拟合。得到如下平滑曲线:
从图 4可知, 日退出率的拟合曲线整体相对平滑, 1月下旬至2月中旬的日退出率较低, 持续在2%左右。此时政府刚开始实施严格管控政策, 且新冠病毒确定人传人的时期是在1月20日左右, 还未引起人们的高度重视, 加之医疗压力较大, 对未知病原体的探索以及有效治疗都进展相对缓慢。随着国家管控政策的全面落实, 各省医疗人员的支援, 检测速度以及治疗水平大幅度提升, 3月份的日退出率出现显著提高。为使模型预测更准确, 去除1月20日之后一个月相应日退出率数据, 确定退出率的期望值为ξ=10.67%。
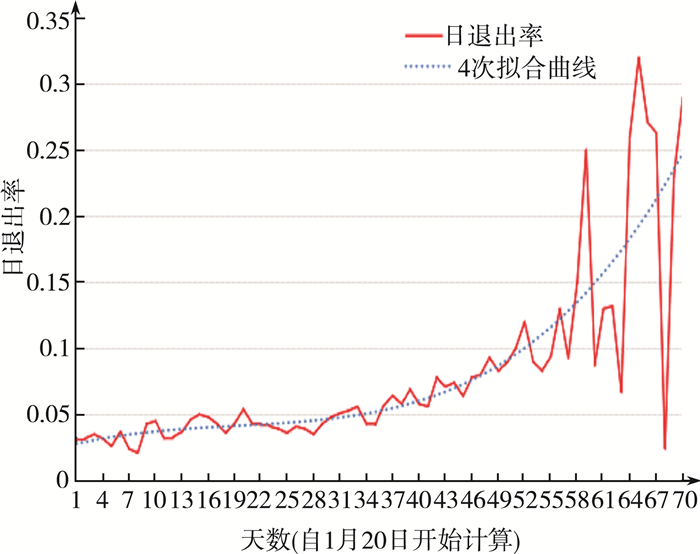 |
| 图 4 1月20日到3月30日日退出率变化曲线图 |
3) 参数λ疑似确诊率
λ=当日疑似病例转为确诊人数/当日疑似病例总数。
从中国疾病预防控制中心官方网站选取1月20日到3月1日每日由疑似转为确诊病人总数和日疑似病例总数[8], 依据上式计算日疑似确诊率, 并对其进行线性拟合及多项式拟合, 详见图 5。
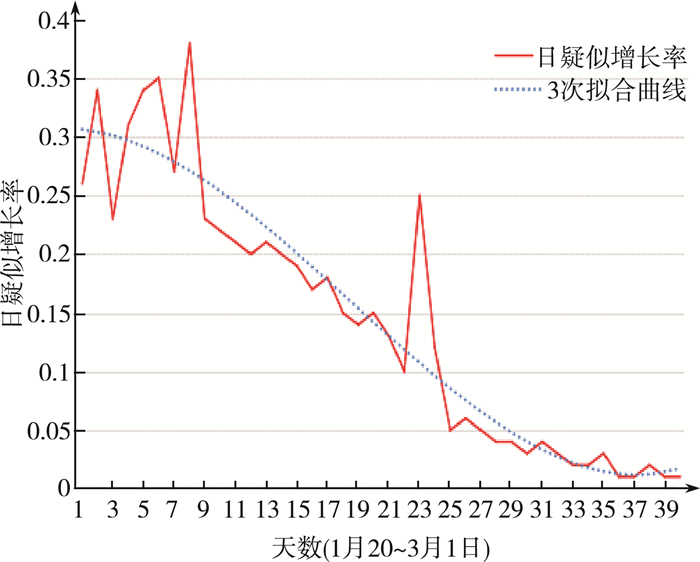 |
| 图 5 1月20日到3月1日疑似确诊率变化曲线图 |
观察分析图 5可知, 整体疑似确诊率呈现一个下降趋势。中间出现一个明显波峰, 是因为当时进行核酸检测的人员增多, 医疗设备充裕, 加之确诊的条件进行扩宽, 故形成往上增长的趋势。在疫情得到充分重视之后, 曲线整体呈现一个单调递减的趋势, 通过统计求解确定日疑似确诊率期望值λ=5.2%。
4) 参数ρ每个病人每天接触的人数
参数与每个人的生活环境、所在地区以及家庭等因素密切相关, 基于相关文献[9], 确定每个病人每天接触人群接触率为45%。
5) 参数ω未隔离者日确诊率
ω=当日未隔离者转为确诊病例的人数/当日未隔离者总数。
根据武汉雷神山、火神山医院提供的一份数据报告[10], 新冠肺炎未隔离者转化为确诊病例的日转化率约在10%~25%之间, 则不妨设ω=19%。
6) 参数θ未隔离者日疑似率
θ=当日由未隔离转为疑似者人数/当日未隔离者总数。
通过查询相关资料[11], 根据官方给出的实时数据, 进行相应求解得未隔离者日疑似率的期望值θ=72%。
基于此, 控制后SIR-YN模型的数值模型如下所示:
| $ \left\{ \begin{array}{l} \frac{{dS\left( t \right)}}{{dt}} = 0.057Y\left( t \right) - 0.45S\left( t \right)N\left( t \right)\\ \frac{{dI\left( t \right)}}{{dt}} = 0.19N\left( t \right) - 0.1067I\left( t \right) + 0.052Y\left( t \right)\\ \frac{{dR\left( t \right)}}{{dt}} = - 0.1067I\left( t \right)\\ \frac{{dY\left( t \right)}}{{dt}} = - 0.057Y\left( t \right) - 0.012Y\left( t \right) + 0.544N\left( t \right)S\left( t \right)\\ \frac{{dN\left( t \right)}}{{dt}} = 0.136N\left( t \right)S\left( t \right) - 0.19N\left( t \right)\\ {S_0} = 0.9997, {I_0} = 1.2783 \times {10^{ - 4}}\\ {R_0} = 1.2977 \times {10^{ - 5}}\\ {Y_0} = 1.2893 \times {10^{ - 4}}, {N_0} = 2.2364 \times {10^{ - 5}} \end{array} 。\right. $ | (9) |
显然, 此模型不存在解析解, 进而化为差分方程进行MATLAB仿真求解[12]。
2.2.5 MATLAB仿真求解预测将模型转为差分方程, 采取模型中的初值, 取时间单位为每日, 模型化为下式:
| $ \left\{ \begin{array}{l} S({t_{i + 1}}) - S({t_i}) = 0.057Y\left( t \right) - 0.45S\left( t \right)N\left( t \right)\\ I({t_{i + 1}}) - I({t_i}) = 0.19N\left( t \right) - 0.1067I\left( t \right) + 0.052Y\left( t \right)\\ R({t_{i + 1}}) - R({t_i}) = 0.1067I\left( t \right)\\ Y({t_{i + 1}}) - Y({t_i}) = - 0.057Y\left( t \right) - 0.012Y\left( t \right) + 0.544N\left( t \right)S\left( t \right)\\ N({t_{i + 1}}) - N({t_i}) = 0.136N\left( t \right)S\left( t \right) - 0.19N\left( t \right)\\ {S_0} = 0.9997, {I_0} = 1.2783 \times {10^{ - 4}}\\ {R_0} = 1.2977 \times {10^{ - 5}}\\ {Y_0} = 1.2893 \times {10^{ - 4}}, {N_0} = 2.2364 \times {10^{ - 5}} \end{array} 。\right. $ | (10) |
基于此模型, 通过MATLAB仿真分别预测健康人数比率、疑似者变化比率、感染者变化比率、退出者变化比率和未隔离者变化比率。
1) 健康人数比率
经图 6的变化曲线分析可得, 对健康人数比率来说, 1月20日专家公布有人传人情况, 由于起初人们重视程度不够加之严防措施不到位等问题, 确诊病例快速上升, 故健康者人数比率曲线会呈现下降趋势。随着政府部门实施严防严控政策, 对流动人口进行管控, 健康人数短暂下降之后逐步呈现上升趋势, 且在2月5日左右开始明显回升。从健康人数比率发展走势来看, 模型预测的结果和实际发展情况可以较好地吻合。
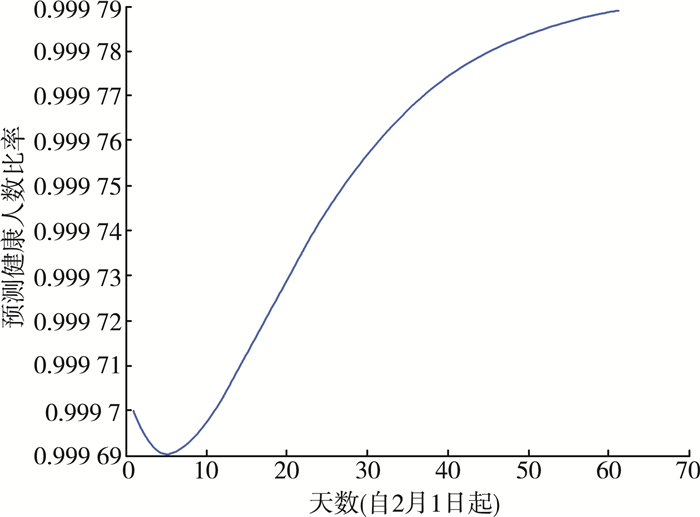 |
| 图 6 健康人数比率趋势图 |
2) 疑似者变化比率
疑似者变化比率曲线一开始呈现先上升后下降的趋势, 符合疫情发展初期疑似者数量变化。随着疫情发展, 医疗人员投入增加, 加之武汉火神山、雷神山医院先后投入使用, 对疑似人员的检测速度增加, 疑似人员后续曲线呈现下降的趋势。
值得注意的是, 疑似者占总人数的比率是跟未隔离不可控人数是有密切关联的, 即ϖ=25%时疑似者变化比率趋势图的数值越大, 那么疑似者所占比率的峰值也会越大。也就是说, 如果一开始措施不及时, 未隔离不可控人数将越来越多, 将严重影响后续疫情的发展。下面通过提高ϖ=25%时疑似者变化比率趋势图数值更直观的来比较, 下取ϖ=25%时疑似者变化比率趋势图=25%, 经MATLAB仿真如下:
将图 7与图 8进行比较, 当ϖ=25%时疑似者变化比率趋势图数值越大时, 模型的峰值也越大, 模型达到峰值后的一段时间里, 疑似人数比率都呈现下降趋势, 但数值越大时曲线下降的速率越慢, 疑似者清零的时间需要更长。即说明控制措施严格实施越早, 可为疫情控制争取更多时间, 控制效果会更明显。
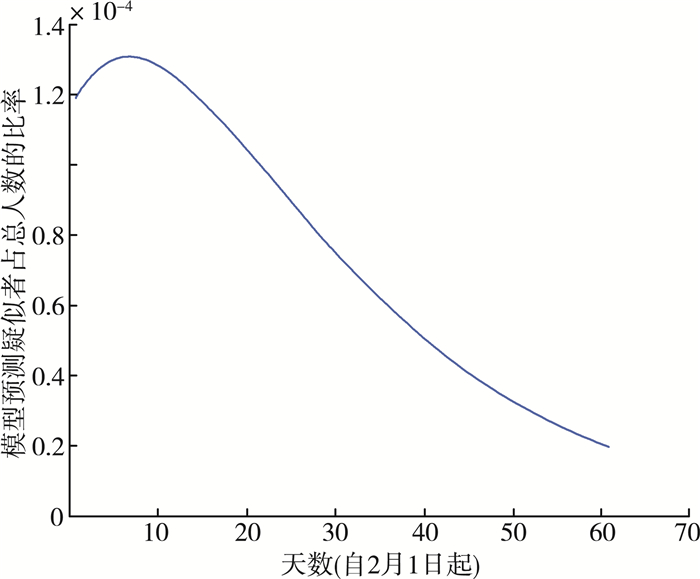 |
| 图 7 ϖ=20%时疑似者变化比率趋势图 |
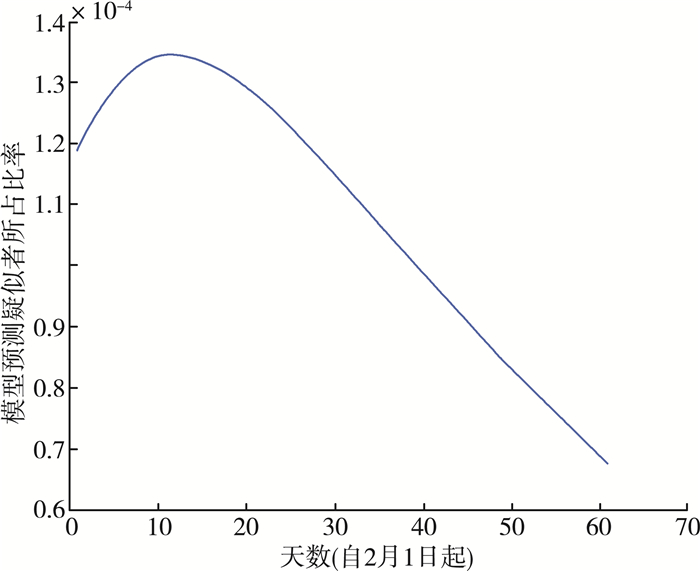 |
| 图 8 ϖ=25%时疑似者变化比率趋势图 |
3) 感染者变化比率
观察分析图 9可知, 随着时间推移, 感染者比率一直呈现下降趋势, 且下降速率越来越慢。虽然中间会存在一些特殊情况, 例如2月11日, 由疑似者转为感染者又呈现明显上升趋势, 因为检测人数增多, 对疑似者进行集中检测导致确诊人数在短时间内快速增多, 此时不具有代表性, 进而模型中没有呈现。在2月11日之后感染者人数又进一步趋于平稳, 所以模型的预测与实际情况的发展基本一致。
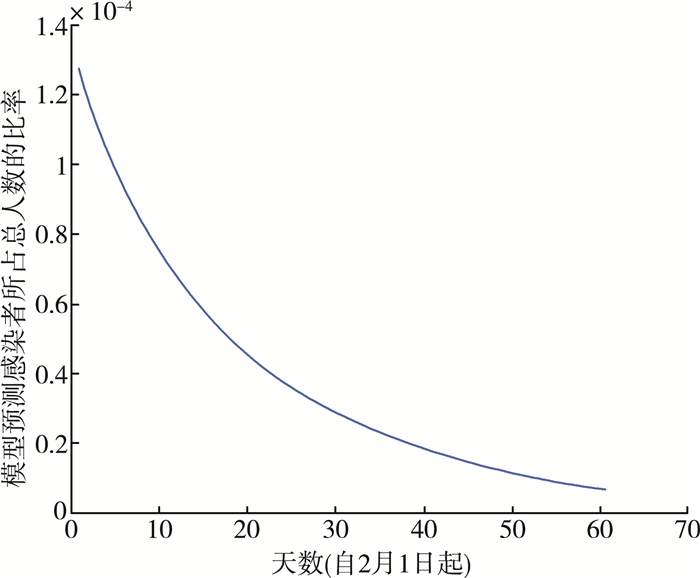 |
| 图 9 感染者变化比率趋势图 |
4) 退出者变化比率
从图 10可知, 自2月1日起, 退出者比率曲线整体呈现上升趋势。在疫情初期, 每日确诊病例和疑似病例总人数大幅度指数上升, 康复者人数相对较少, 曲线一开始上升较慢。后续医疗条件逐渐满足需求, 此时康复率增高死亡率降低, 退出者的比率也得益快速增长。后随着感染人数越来越少, 退出者的比率得以逐渐平稳。模型预测与实际情况发展基本吻合。
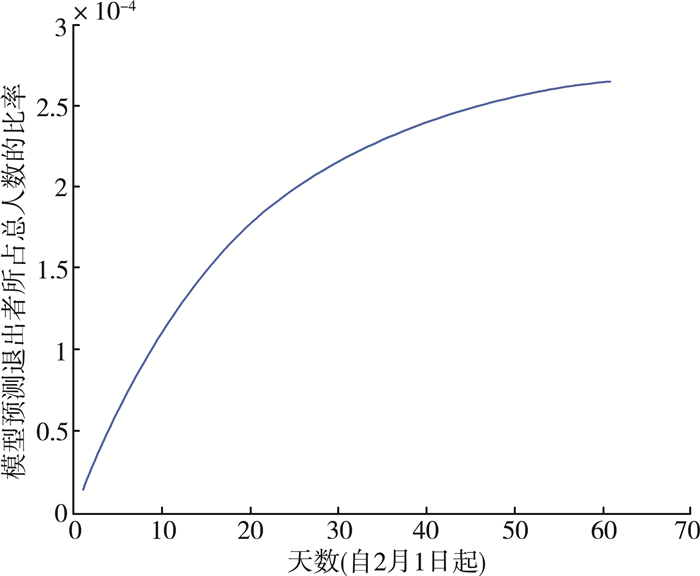 |
| 图 10 退出者变化比率趋势图 |
5) 未隔离者变化比率
从图 11可知, 曲线整体呈现下降趋势, 且曲线一开始下降较快, 后续下降较慢进而趋于平稳。这是由于1月底, 全国已严格实施管控措施, 人们对新冠疫情的防范认识逐渐提高, 有症状的患者积极配合治疗或者进行居家隔离, 密切接触者减少, 故曲线呈现下降趋势。随着时间推移, 患病者被逐步全部隔离, 有疑似症状者的数量也逐渐减少, 后趋于稳定。整体来说模型预测曲线与实际发展相吻合。
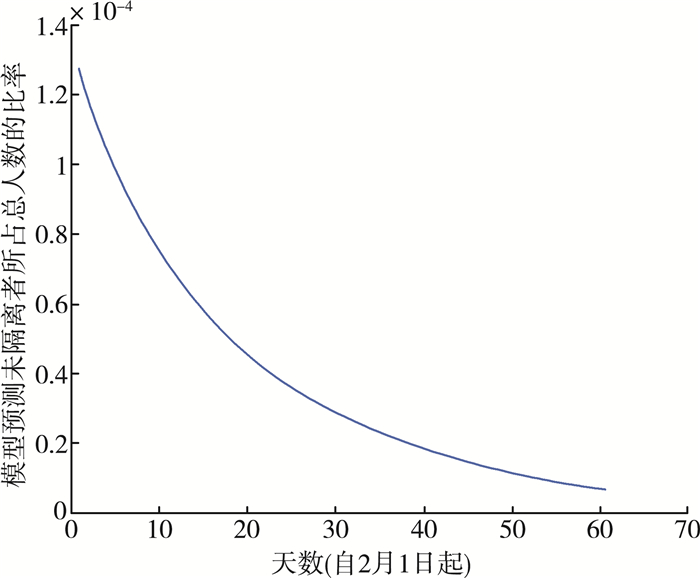 |
| 图 11 未隔离者变化比率趋势图 |
3 总结
对照官方公布的真实精确数据, 借助传染病模型对某一具有代表性地区分别建立控制前与控制后模型, 得到如下结论:
1) 政府采取的居家隔离、封城、公共领域限制等一系列持续地严防严控举措对减缓疫情传播速度起到非常显著的作用, 进而降低疫情传播规模, 且越早隔离越有助于控制疫情发展趋势, 为控制疫情发展争取到更多主动权。
2) 对疑似感染者集中快速隔离和诊断是疫情防控中的重要环节, 每日新增确诊病例中很大比例由疑似感染者转化而来, 可知强制隔离观察和快速诊断措施可缩减疫情扩散区域, 阻碍疫情多点散花似扩散。
3) 优质且全方位覆盖的公共卫生基础设施和高质量的公共卫生治疗水平是政府应急处理突发公共卫生事件, 把事件扼杀在萌芽之时的重要保障。
| [1] |
WORLD HEALTH ORGANIZATION.Coronavirus disease(COVID-2019)situationreports[EB/OL].[2020-07-13].https://www.who.int/.
|
| [2] |
徐瑞, 田晓红, 甘勤涛. 传染病动力学建模与分析[M]. 北京: 科学出版社, 2018: 129-169.
|
| [3] |
韩翔, 夏苏徽. 基于SIS模型的禽流感传染模型[J]. 现代商贸工业, 2018, 39(22): 80-81. |
| [4] |
尹楠. 基于SIR模型的有限区域内新冠肺炎疫情传播仿真模拟[J]. 统计与决策, 2020, 36(05): 15-20. |
| [5] |
王双明, 樊馨蔓, 张明军, 等. 具周期性潜伏期的SEIR传染病模型的动力学[J]. 数学物理学报, 2020, 40(02): 527-539. |
| [6] |
潘锋. 新冠肺炎疫情下普通外科需格外重视防护问题——访中国科学院院士、同济医学院附属同济医院陈孝平教授[J]. 中国医药导报, 2020, 17(11): 1-3. |
| [7] |
邱明悦, 胡涛, 崔恒建. 双区间删失下新冠病毒肺炎潜伏期分布的参数估计[J]. 应用数学学报, 2020, 43(02): 200-210. |
| [8] |
中国疾病预防控制中心.疫情动态[EB/OL].[2020-03-30].http://www.chinacdc.cn/jkzt/crb/zl/szkb_11803/.
|
| [9] |
范如国, 王奕博, 罗明, 等. 基于SEIR的新冠肺炎传播模型及拐点预测分析[J]. 电子科技大学学报, 2020, 49(03): 369-374. |
| [10] |
薛鑫, 韩黎, 李海峰, 等.武汉火神山医院感染防控技术指引体系建设[J/OL].中华医院感染学杂志, [2020-07-15].http://kns.cnki.net/kcms/detail/11.3456.R.20200622.0845.002.html.
|
| [11] |
李丽, 钱招昕, 潘频华, 等.新型冠状病毒肺炎隔离病区医务人员职业风险与防控对策[J/OL].中国感染控制杂志, [2020-07-15].http://kns.cnki.net/kcms/detail/43.1390.R.20200520.1353.008.html.
|
| [12] |
王正林, 刘明. 精通MATLAB[M]. 北京: 电子工业出版社, 2006: 3-65.
|
 2020, Vol. 34
2020, Vol. 34


