| 车联网中三种自适应协同通信算法性能比较 |
2. 济南市章丘区国网供电公司,济南 250200
2. State Grid Zhangqiu Power Supply Company, Jinan 250200, China
车联网具有节点运动速度快、网络拓扑结构变化频繁、衰落严重等特点。为了保证车与车之间信息传递的快速性与准确性,将协同通信引入车联网并针对不同情况选择合适的自适应协同通信算法至关重要。文献[1]研究了多中继解码转发网络中的中继选择方案,并分析了协同通信系统的误码率SER性能,但在中继选择方案中没有考虑中继节点的错误检测问题。文献[2]研究了多跳分集传输系统中的选择解码转发中继传输问题,提出了一种基于源端-中继端瞬时接收信噪比的中继选择方案。文献[3]研究了无线多播多跳网络中基于端到端容量的协同路由选择算法,并分析了其性能。上述文献主要研究了中继节点为静止状态下的中继选择方案,而没有分析中继节点为运动状态时的情况,这使得协同中继传输算法在车联网中的应用存在一定的局限性。文献[4]提出了一种车联网中基于博弈论的中继选择算法,但其算法十分复杂,这无疑提高了车辆节点的运算压力。文献[5]研究了基于车流密度的车联网中继选择算法,该算法主要分析了源节点和中继节点的发射功率随车流密度大小自适应调整的问题,而对中继选择算法没有做详细研究。
因此,本文研究了应用于车联网的三种自适应协同算法并展开分析对比。鉴于解码转发(DF)具有解码检测的特性,首先选用了DF协同通信方式,然后提出了适用于车联网中三种不同且算法复杂度低的自适应协同通信传输算法,分别是随机选择传输路径算法(RP)、基于最佳信道特性的传输路径算法(OPCG)、基于丢包率最小的传输路径算法(OPLR);再次研究了在不同路径衰落指数与不同中继节点运动速度情况下,基于上述三种算法的系统误码率性能;最后在比较三种算法性能的基础上,分别给出了其相应的应用场景。仿真结果表明,OPCG性能最优,但车辆低速行驶时,三种算法性能差别很小,RP即可满足要求,OPLR适用于时延不敏感的场景。
1 系统模型车联网中的信息传输多为多跳中继协作方式,在此为了简化分析,考虑一个简单的单个源端S、多个中继端r与单个目的端D组成的两跳信息传输模型。其中源端S与目的端D为静止状态,中继节点的运动轨迹假定服从随机路点模型。中继传输方式为采用循环冗余校验CRC的解码转发(DF)方式。如图 1所示,其中蓝色的节点分别表示源节点与目的节点,其他的为能正确解码源端信息的节点,将其称之为潜在中继节点;带箭头的实线表示可能存在的中继传输路径,考虑到协同通信模式,直传链路S-D一直参与信息传输。
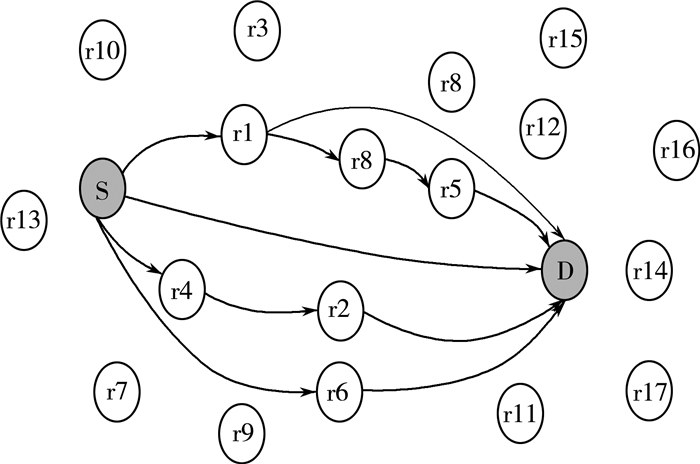 |
| 图 1 多中继车联网系统模型 |
在两跳中继传输模型中,协同通信过程由两个阶段构成。第一阶段,源节点向目的节点和所有的潜在中继节点进行信息广播;第二阶段,潜在中继节点向目的节点进行解码转发第一阶段接收到的信息。所有阶段中,信息的广播都是通过TDMA、FDMA或CDMA方案的正交信道发送信息。
在第一阶段,源节点向目的节点和中继节点广播信息,只有能够正确解码的中继才能称为潜在中继,因此目的端和第i个潜在中继端的接收信号ysd和ysri的表达方式如下:
| $ {y_{sd}} = \sqrt {{P_s}} {h_{sd}}x + {\eta _{sd}} $ | (1) |
| $ {y_{s{r_i}}} = \sqrt {{P_s}} {h_{s{r_i}}}x + {\eta _{s{r_i}}} $ | (2) |
其中:Ps为源端的发送功率,x为源节点的发送信号, ηsd与ηsri为方差为N0的加性高斯白噪声。
在第二阶段,潜在中继节点转发成功解码后的信息,目的节点接收信号表达方式如下:
| $ {y_{rd}} = \sqrt {{P_r}} {h_{{r_i}d}}x + {\eta _{{r_i}d}} $ | (3) |
其中:Pr为中继端的发送功率,ηrid为方差为N0的加性高斯白噪声。
公式(1)~(3)中,Ps+Pr=P,Ps=Pr=0.5P,P为总的传输功率。hm, k(m∈{s, ri}, k∈{ri, d})为发送端与接收端之间的信道衰落系数。假定接收端获知信道状态信息,而发送端则只知道统计信道状态信息。系数hm, k均为满足独立、循环对称复高斯分布的随机变量,均值为零,方差为σm, k2。与此同时,σm, k2用于组建路径衰落模型,如公式(4)所示。dm, k表示m节点与k节点之间的距离,n表示路径衰落系数。综上所述,包络|hm, k|服从瑞利分布,包络的平方|hm, k2|服从参数为
| $ \sigma _{m, k}^2 \propto d_{m, k}^{ - n} $ | (4) |
根据车联网中车辆节点信息传输的特性,提出了三种不同的自适应中继传输方法,分别是:随机选择传输路径RP算法、基于最佳信道特性的传输路径算法OPCG、基于丢包率最小的传输路径算法OPLR。算法具体描述如下所示。
2.1 RP算法随机选择传输路径RP算法,即在能正确解码源节点信息的潜在中继节点中,随机选择一个中继节点来协助源节点信息的传输。
该算法简单可行,但潜在中继节点显然仅考虑了源-中继节点间的信道特性,随机选择潜在中继节点进行信息的转发并没有考虑到中继-目的节点的信道特性,其性能一定是最差的。
2.2 OPCG算法基于最佳信道特性的传输路径OPCG算法中,首先从能够正确解码源端信息的潜在中继中进行选择,这相当于已经考虑到源-中继端的信道状态信息;然后再从潜在中继中选取与目的节点D的信道传输特性最好的中继Ri进行信息转发,即如公式(5)所示:
| $ {R_i} = \mathop {\arg \;\max }\limits_{{r_i} \in D\left( s \right)} \left\{ {{{\left| {{h_{{r_i}d}}} \right|}^2}} \right\}, i = 1, 2 \cdots \left| {D\left( S \right)} \right| $ | (5) |
式中|D(S)|为对源节点S信息解码成功的潜在中继节点集合。
可见该算法综合考虑了源-中继以及中继-目的节点的信道传输特性,其性能一定是最优的,并且车速越快其优越性体现的越明显,但随着车速的增加需要时时对比各中继传输信道的优劣,算法的复杂性亦会随之增加。
2.3 OPLR算法基于丢包率最小的传输路径OPLR算法,该算法借鉴了机会路由协议(ExOR)期望传输次数(ETX)思想[7]。首先分别求得源节点-中继节点的丢包率LRsrj、中继节点-目的节点的丢包率LRrjd,然后综合考虑两条路径的丢包率调和值,选择ETX值最大即丢包率最小的路径作为信息传输路径。如式(6)所示。
| $ \begin{array}{l} \;\;\;\;ET{X_j} = \mathop {\arg \;\mathit{max}}\limits_{{r_j} \in F\left( S \right)} \left\{ {\frac{1}{{L{R_{s{r_j}}}}} + \frac{1}{{L{R_{{r_j}d}}}}} \right\}, \;j = 1, \\ 2 \cdots \left| {F\left( S \right)} \right| \end{array} $ | (6) |
式中|F(S)|为协助源节点进行信息传输的中继节点集合。
丢包率的获得通过NS2[8]仿真平台实现。其仿真场景为:仿真区域为4 100 m×2 500 m,仿真时间设置为100 s,车辆节点数目设置为52;源节点和目的节点都为静止状态,源节点位置为(1 260,1 340)m,目的节点位置为(2 700,1 600)m,中继节点为运动状态,运动轨迹服从随机路点模型;针对城市中车辆运动的特点,车辆节点移动速度分别设置为5 m/s、16 m/s;数据包类型采用CBR数据流,通信数据包大小设置为128 byte;路由算法为AODV。
将上述NS2中信息传输的过程移植到MATLAB中,然后与RP、OPCG的性能进行分析比较。
该算法借鉴了跨层的思路,将上层的丢包率性能作为选择路径的依据,因此更加吻合实际传输特性,但因为要计算丢包率再来选择传输路径,这也会带来明显的缺点,即实时性差。
3 仿真结果分析为了模拟车联网中的车辆运动状态,以及在该运动状态下分析对比RP、OPCG、OPLR三种算法,采用Monte Carlo方法对系统误码率性能进行计算机仿真。同时,为与NS2中的仿真条件保持一致,具体仿真条件设置如下:仿真范围4.1×2.5 km,源节点位置为(1.26,1.34)km,目的节点位置为(2.7,1.6)km,采用随机路点模型来模拟中继节点的运行状态;调制方式采用QPSK;噪声方差N0=1;信道hs, r、hs, d、hr, d均服从独立复高斯分布,且其方差由路径衰落模型σm, k2∝dm, k-n决定,衰落指数n分别取1和4,车辆节点移动速度分别设置为5 m/s、16 m/s。以下比较了中继节点不同运动速度v、不同路径衰落指数n情况下,分别通过RP、OPCG以及OPLR进行信息传输的误码率性能。
图 2比较了n=1时,中继节点在不同运动速度下通过OPLR、OPCG以及RP进行信息传输的误码率性能。由图可见,n=1时,不同速度下通过以上三种方式进行信息传输的SER相差无几。这是因为路径衰落指数小时,路径的变化对信道的影响也很小,OPCG算法的优越性无从体现。
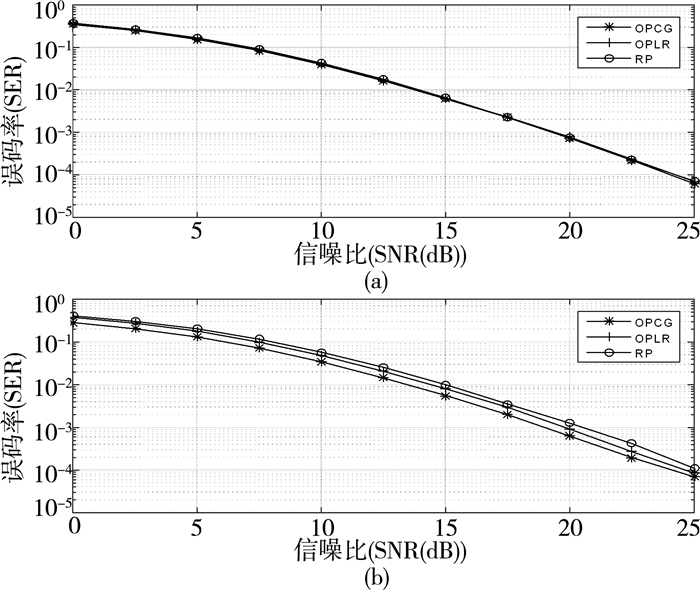 |
| 注:(a)v=5 m/s,(b)v=16 m/s 图 2 衰落指数为n=1时两种速度情况下不同自适应协同算法的SER性能比较 |
图 3比较了n=4时,中继节点在不同运动速度下通过OPLR、OPCG以及RP进行信息传输的误码率性能。如图所示,v=5 m/s时,通过以上三种方式进行信息传输的SER几乎无差别,这是因为节点运动速度小时,网络的拓扑结构变化很小且不会发生突变,因此信道传输特性变化不是很大。但当v=16 m/s时,由OPCG进行信息传输的SER性能明显优于其他两种方式。如误码率为10-2时,相对于OPLR,通过OPCG进行信息传输可取得大约2.5 dB的信噪比增益。
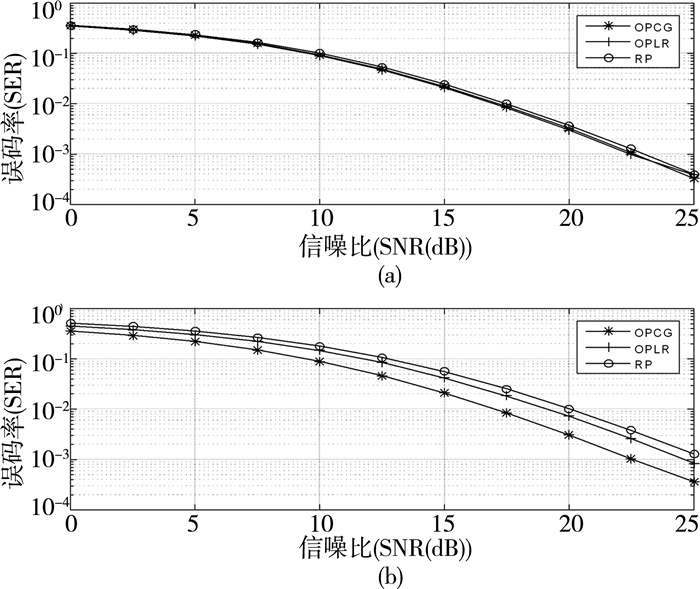 |
| 注:(a)v=5 m/s,(b)v=16 m/s 图 3 衰落系数n=4时两种速度情况下不同自适应协同算法的SER性能比较 |
图 4比较了n相同时速度对三种不同自适应协同通信算法性能的影响。由图可以看出,速度的变化对OPCG算法的性能影响较小,但是随着速度的增大,RP、OPLR算法的误码率性能明显变差。这说明OPCG算法能够适应车联网中节点高速移动的情况。
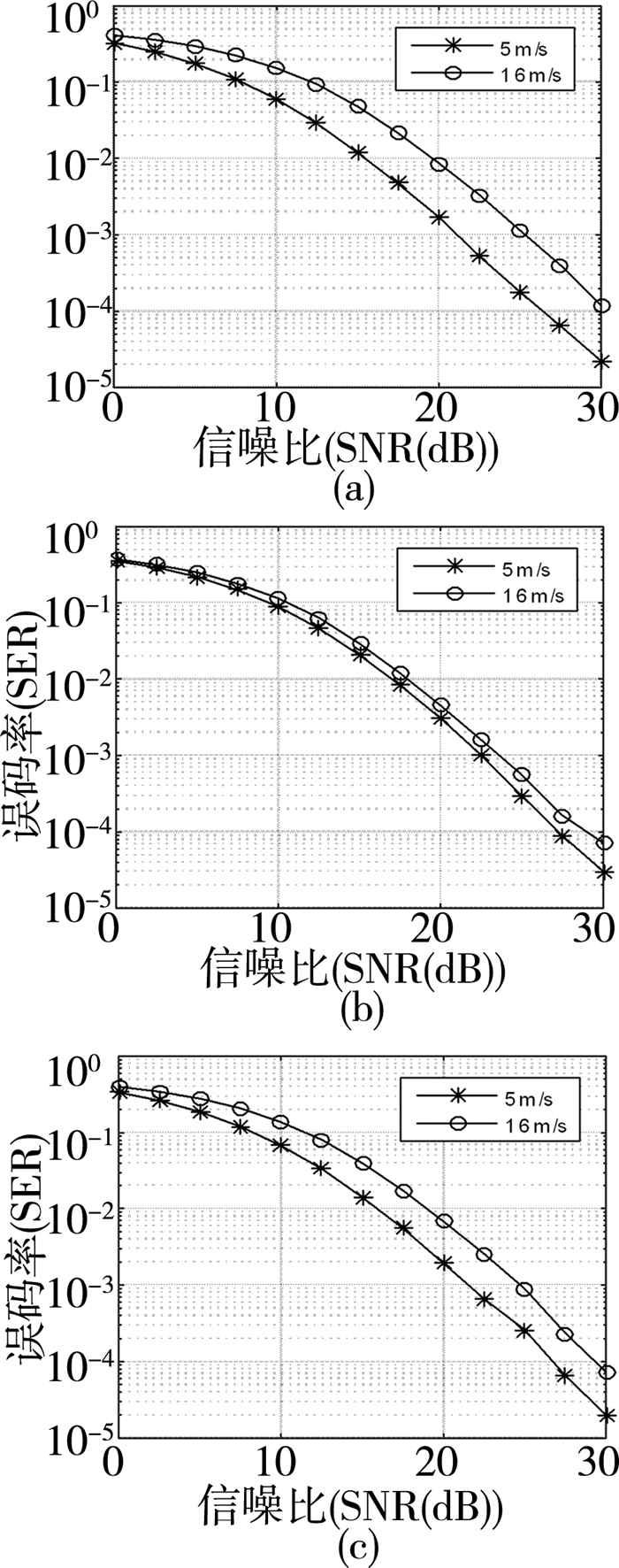 |
| 图 4 衰落系数n=4时不同速度对三种算法性能的影响 |
根据以上理论与仿真分析,表 1给出了OPLR、OPCG、RP的特点和适用场景。
| 表 1 三种算法的特点与适用场景 |
 |
综合图 2~4以及表 1可知:车辆节点运动速度小时,通过OPLR、OPCG以及RP三种算法的误码率性能相差无几,此时选择最简单的RP进行信息传输即可满足要求;当节点运动速度变大时,通过OPCG进行信息传输的优势变得明显,其误码率最小,此时应选择OPCG;OPLR则适用于时延不敏感的场景。
4 总结研究了车联网中不同的自适应中继传输方法的性能问题。首先提出了适用于车联网中三种不同的自适应协同通信算法,分别是:随机选择传输路径RP算法、基于丢包率最小的传输路径OPLR算法、基于最佳信道特性的传输路径OPCG算法;然后研究了在不同路径衰落指数与不同中继节点运动速度情况下,基于三种算法的系统误码率性能;最后在比较三种算法性能的基础上,分别给出了其相应的应用场景。仿真结果表明:OPCG性能最优,但车辆低速行驶时,三种算法性能差别很小,RP即可满足要求,OPLR适用于时延不敏感的场景。
该研究是在多中继节点运动的情况下进行的,但源节点和目的节点均为单一的且为静止状态,为了更贴近车联网的运动状态,多源端-多中继端-多目的端且均为运动状态下进行信息传输的性能分析将是我们下一步工作的方向。
| [1] |
FAREED M M, UYSAL M. On relay selection for decode-and-forward relaying[J]. IEEE Transactions on Wireless Communications, 2009, 8(7): 3341-3346. DOI:10.1109/TWC.2009.071306 |
| [2] |
FARHADI G, BEAULIEU N C. Selective Decode-and-Forward Relaying Scheme for Multi-Hop Diversity Transmission Systems[C]//Global Telecommunications Conference, 2007. GLOBECOM'07. IEEE. IEEE, 2007: 4385-4390. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4411744
|
| [3] |
XIE K, WANG X, WEN J, et al. Cooperative routing with relay assignment in multiradiomultihop wireless networks[J]. IEEE/ACM Transactions on Networking, 2016, 24(2): 859-872. DOI:10.1109/TNET.2015.2397035 |
| [4] |
杨宾. 车联网中继选择算法研究[D]. 重庆: 重庆邮电大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10617-1014066133.htm
|
| [5] |
比拉, 刘佳, 郭爱煌. 基于车流密度的车联网城市场景中继选择算法[J]. 通信技术, 2017, 50(1): 50-55. |
| [6] |
GOLDSMITH A. Wireless Communications[M]. 1th ed. England: Cambridge University Press, 2005.
|
| [7] |
BISWAS S, MORRIS R. ExOR: opportunistic multi-hoproutingforwirelessnetworks[C]//Conference on Applications. ACM, 2005: 133-144. http://dl.acm.org/citation.cfm?id=1080108
|
| [8] |
ISSARIYAKUL T, HOSSAIN E. Introduction to Network Simulator NS2[J]. Springer Berlin, 2012, 3: 21-40. |
 2018, Vol. 32
2018, Vol. 32


