| 基于半色调数字图像的抗打印的水印算法研究 |
数字水印在数字图像基础上, 将一些编码信息嵌入到宿主图像中, 不可见水印更要求隐藏不被人眼识别, 但通过相应的算法又可以检测和提取出嵌入的信息。目前研究较多的是在连续调图像中嵌入水印[1-4]。在打印和印刷时, 连续数字图像首先要进行加网和分色处理, 原来嵌入的水印信息在这个过程中会发生很大变化, 检测时再经过扫描重新采样量化, 就不易被检测出来了。研究在灰度图像加网的过程中嵌入水印, 是实现印刷水印关键的一步。包装中使用了大量的印刷品, 印刷水印技术含量高又环保, 对于实现包装防伪有重要意义。虽然印刷水印的研制引起了多方的关注[5-8], 至今市场上还没有出现不可见的印刷数字水印用于包装防伪, 所以本课题是重要的创新性实践。本文对数字加网技术进行了概述, 并实现了两种半色调水印算法。为了保障防伪价值, 我们提出了以下的设计目标:水印在第一次打印输出时可以被确实检测, 经过二轮扫描打印, 水印信息被破坏、不能检测出来, 因此可以防范包装非法复制。
1 半色调图像生成算法半色调图像利用了人眼感知特性, 以一定分辨率的离散网点模拟连续图像的视觉轮廓和阶调分布。在灰度图像上进行加网操作就得到半调化图像, 它是各种打印、印刷设备的基础。
灰度图像的半调化方法也很容易扩展到彩色图像的应用中。下面, 我们对常用的数字加网算法(模式抖动、误差扩散、点扩散和视觉迭代)进行概述。
1.1 模式抖动算法最具代表性的是拜耳抖动加网算法[9-10]。这种方法利用域值矩阵来对一幅图像进行二值化处理。其中拜耳高阶矩阵可以很容易地从低阶矩阵中迭代生成。待加网的图像按照抖动矩阵的大小划分成块矩阵, 在块内按抖动矩阵设定的阈值进行二值化。拜耳抖动矩阵生成的公式如下:
| ${D_n} = \left[ {\begin{array}{*{20}{c}} {4{D_{n/2}}}&{4{D_{n/2}} + 2{U_{n/2}}}\\ {4{D_{n/2}} + 3{U_{n/2}}}&{4{D_{n/2}} + {U_{n/2}}} \end{array}} \right]$ | (1) |
Dn是n阶拜耳矩阵, 一个2n×2n的抖动矩阵。Un是2n×2n的单位矩阵。设定D0=0;应用上面的公式迭代计算, 可以生成n阶的拜耳抖动矩阵。拜耳抖动矩阵有很好的对称性, 能实现较好的视觉效果, 但效果有些呆板, 常用作高分辨率输出。
1.2 误差扩散算法1975年FLOYD-STEINBERG提出了过滤器法[11-12]。它实际上就是一个误差分配表, 对于一个像素值, 根据初始阈值二值化处理后, 由其所产生的误差将会被分散到近邻的四个像素点上。误差分配矩阵决定误差的扩散方向和大小, 误差分配表的设计一般要考虑到人的视觉系统对水平、垂直方向的误差的感知差异, 达到视觉上的平衡感受。
1.3 点扩散算法1987年D.E.KNUTH提出的点扩散算法是一种结合有序抖动思想和误差扩散思想的算法。首先将待处理的图像数据划分成8×8单元的块矩阵。块间同等级别的像素同步处理。块内将图像像素的处理顺序划分成许多等级, 由一个点扩散等级矩阵(8×8的矩阵)控制。点扩散矩阵同样要考虑人的视觉特性, 它可以消除与图像扫描顺序相关的图像退化现象, 对称性好。
1.4 视觉迭代算法迭代半色调算法的思想是先用一种简单的方法, 如拜耳抖动、误差扩散或点扩散方法加网, 得到初始的半色调图像, 然后对初始半色调图像进行局部微调迭代处理, 使每次处理得到的半色调图像相比原来的连续调图像具有更小的误差, 最后得到视觉优化的半色调图像。二元搜索(DBS)是一种常见的视觉迭代算法[13-15]。迭代半色调算法得到的图像视觉效果非常优秀, 但是由于计算复杂, 一般用来进行其他图像处理的微调优化。
2 半色调水印实现框架按水印嵌入处理的方法不同, 可以将图像数字水印技术分成空域和变换域算法两大类。变换域算法需对原始图像进行离散余弦变换或小波变换, 再嵌入水印信息。变换域算法是对连续调图像进行处理。本文主要研究半色调水印的实现方法。结合查阅的文献, 我们提出一个半色调水印实施框架,如图 1所示。
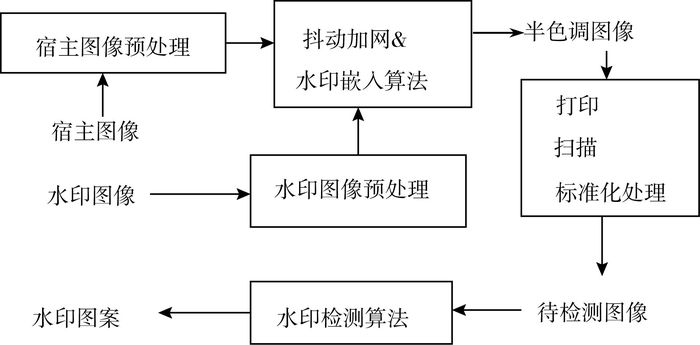 |
| 图 1 基于半色调图像的打印水印实现框架 |
内容概括如下:
1) 预处理部分主要包括图像去噪、平滑等优化处理。水印图案预处理包括二值化或其他压缩编码处理。
2) 加网合并水印嵌入算法。使用各种数字加网算法, 将连续调图像进行二值化。设计水印嵌入算法, 在加网处理过程中, 将水印信息嵌入到加网图像中。
3) 图像输出和扫描。半色调图像经过打印和扫描, 重新数字化的图像需要定位对齐, 再经过阈值设定和标准化, 得到分辨率一致的待检测二值图像。
4) 水印提取是水印嵌入的逆运算。检测出的水印图像可能还需要采用形态学等方法进行恢复和识别。
3 打印水印嵌入与检测算法图 1描述的半色调水印的实现框架中, 不同的水印算法体现在第二步和第四步的不同, 而第四步又是第二步的逆运算。目前我们实验了两种方案:1)基于视觉迭代的水印算法; 2)基于拜耳抖动核的水印算法。第一种算法的具体实现和实验数据详细记录在已经发表的论文[16]中,本文仅做简单介绍。
3.1 基于视觉迭代的水印算法此算法水印嵌入量大, 视觉质量好。
1) 选用一种加网算法将连续调图像进行二值化, 同时对嵌入的数字水印图案也进行二值化处理。
2) 使用随机数种子作密钥, 产生一系列二维随机数对, 作为水印像素序列的嵌入位置。
3) 水印图像是二值化图, 每一个像素的值是0或1。将此二值水印图像转变为一个二值序列, 在上一步产生的随机位置上依次嵌入水印序列值。
4) 嵌入水印后, 使用视觉迭思想对嵌入水印的图像进行视觉优化, 始终保持嵌入位置的水印信息不变, 而改变邻域的网点分布情况, 隐藏嵌入痕迹。
水印提取过程也是一个解密过程, 传递的密钥是这个过程的安全保证。通过密钥解析水印嵌入位置, 提取出水印像素序列的对应数值。
3.2 基于拜耳抖动矩阵的水印算法使用公式(1), 设定不同D1可以迭代生成不同的D3抖动矩阵, 这里称D1为抖动核矩阵。如果用不同抖动核对图像局部进行抖动,不但有可能弱化人工纹理的瑕疵, 更重要的是, 不同的抖动核也可以看成是对水印信息的一种编码方式, 自然而然地将水印信息嵌入到半色调图像中。由8×8小块的加网模式对水印编码嵌入比起单个嵌入的像素点, 无疑具有更好的抵抗打印和扫描攻击的能力。加网效果可以图 2为例说明:
 |
| 图 2 像素点灰度值为127的图块的两种加网效果 |
1) 选择不同的抖动核D1、D1′, 按照公式(1)的方式迭代计算, 生成两个不同的三阶拜耳抖矩阵D3和D3′。
2) 将整个宿主图像线划分成8×8的小块, 每一个小块对应一位水印像素值0或1。
3) 将水印像素嵌入图像。如果当前水印像素是1, 用D3抖动矩阵二值化当前的8×8小块;如果水印像素是0, 则用D3′抖动矩阵二值化当前的8×8小块。
水印的识别是一个逆过程。基于我们对拜耳抖动原理的认识, 局域8×8小块的平均灰度一样时, 通过选择两种抖动核, 可以分辨出不同的抖动模式。
水印检测的算法如下:
① 对扫描打印图像进行定位、对齐、缩放和阈值设定,得到待检测的二值图像。
② 将图像划分为8×8的小块, 逐行逐列检测每一个小块。求小块中像素的平均值PM。
③ 对应生成一个灰度为PM的8×8小块, 对这个均值矩阵分别用M1和M2两种嵌入时选择的矩阵进行抖动, 将抖动得到的两种结果与扫描图像中对应实际得到的小块加网模式比较。我们采用欧式距离进行计算模式之间的相似度。距离小就是表示相似度高。
4) 根据模式相似度比较, 就可以还原出每一个小块对应的水印数据。
4 实验与讨论首先进行了基于离散像素的水印嵌入方案, 对点扩散加网方法全局阈值设定进行了改进, 对图像分块计算局部阈值, 提高了算法的效果。用Matlab时间截取函数, 在运行时得到时间相关的子串作为密钥, 并以此为种子, 使用随机数生成函数,产生全局随机分布的嵌入位置数组, 将水印信息按原样顺序嵌入离散位置中。嵌入水印后的图像产生了一些差别, 此时对照原始连续调图像, 实现了一个视觉迭代算法, 隐藏嵌入水印的痕迹。利用传递的密钥(随机数种子)可以恢复水印嵌入位置数组, 并且完整恢复嵌入的水印图案像。然而, 在打印和扫描的实验中, 没有检测出水印图案。分析原因是在图像转移的过程中存在图像的对齐误差、缩放误差、打印扫描传递误差等, 导致基于单个像素点的水印信息不易恢复出来。通过下面的模拟实验来证实上述猜想。模拟实验通过小角度的旋转来模拟图像传递误差。实验表明, 随机嵌入多重水印时, 会因为水印像素位置重叠而造成一些信息损失。同时小角度的旋转误差确实会导致水印信息检测困难。
在基于邻域抖动核编码的实验中, 实验素材如图 3所示, 宿主图像文件名为“pelicans”, 具有256级灰度, 图像的分辨率是512×512。二值图“nice work”依然作为水印图案, 为了计算方便, 这里缩小为64×64的分辨率。
 |
| 图 3 宿主图像 |
首先将宿主图像划分为64×64个8×8的小块, 分别对应64×64水印图案的每一个像素。然后对宿主图像逐块进行抖动。如果对应的水印图案像素为1,用抖动核M1进行抖动;如果水印图案像素为0, 用抖动核M2进行抖动加网。其中:
| ${M_1} = \left[ {3\;1;2\;0} \right]\quad \quad {M_2} = \left[ {0\;2;3\;1} \right]$ |
按照拜耳抖动矩阵的生成公式, 可以迭代生成两个8×8的抖动矩阵, 其中M2是我们常用的拜耳矩阵核。我们可以任意设计不同的抖动核, 对同样的均值灰度块用两种抖动核进行加网。对于不同加网核产生的加网结果, 模式相似性越小越好。M1是我们在实验中发现的较好的抖动核。按照算法2, 水印信息嵌入之后, 原来的连续图像也转化为半色调图像,如图 4所示。
 |
| 图 4 嵌入水印的半色调图像 |
图 4中的图像经过打印和扫描后,会产生一定程度的信号衰变。经过人工对齐缩放得到的512×512像素的图像, 作为待检测图像,如图 5所示。
 |
| 图 5 扫描标准化半色调图像 |
在检测水印的时候, 使用算法3, 先计算每一个小块B的累积像素和, 表示灰度的级别, 将这个积乘以4作为灰度均值, 可以生成一个均值灰度块H。对这个灰度块H用两个抖动核加网。得到两个基准加网块HM1和HM2。然后分别计算B与HM1和HM2的相似程度, 这里选用矢量的欧氏距离d1和d2来表示。如果d1>d2,就可以认为B更有可能是从M1加网的到的, 因而对应的水印像素是1;反之, 水印像素位为0。逐块检测扫描图, 最终可以检测出64×64个像素组成的水印检测图案,如图 6所示。
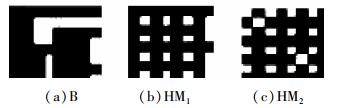 |
| 图 6 图块模式比较 |
如图 6的情况:d1=3,d2=4.5826,可以判断B更可能是1的编码。按上面的方法检测每一个8×8子块, 从扫描图中提取出的水印检测效果明显, 不过检测出的水印不完整。如果对扫描图像进行小角度的旋转和进行不同阈值设定,可以又得到不同的水印检测图案,如图 7所示。
 |
| 图 7 小角度旋转和阈值设定下检测出的水印图案 |
从图 7中, 可以发现一个有趣的现象:检测出字母N所在部分与原来的嵌入像素值正好相反, 而字母C却没有反向。说明经过打印和扫描,加网模式发生了很大的偏移, 甚至反向, 但是临近的相同编码的子块偏移量是相似的, 所以同样可以检测出水印图案。因此可以得出结论:水印信息衰减在图像不同位置不一样的, 而且模式衰减在连续的区域也是连续变化的。这样的偏移也保证了经过二轮打印和扫描, 水印信息完全破坏, 就很难检测出了。
5 结论研究与实验表明, 半色调图像嵌入水印是一种高效可行的水印算法。同时, 半色调图像水印的成功只是印刷水印实现的第一步, 在之后的打印和扫描数字化过程中还有很多难点问题需要解决, 如图像准确定位和对齐、打印模型和扫描模型对网点布局的影响。实验表明,基于邻域编码的半色调水印算法比离散单像素嵌入的水印有更强的鲁棒性。
因为水印信息的检测是通过对不同加网模式的识别得到的,如果能够预测打印扫描后重新采样的图像的网点布局, 建立印刷中智能化图像转移模型, 就有可能检测出完整的水印信息。例如选择较成熟的模式识别工具,如:神经网络、卷积神经网络、SVM等,找到自适应的嵌入和识别半色调图像水印信息的方法。
| [1] |
霍畅. 图像数字水印算法的研究及嵌入式实现[D]. 长春: 东北师范大学, 2011. http://d.wanfangdata.com.cn/Thesis/J0058708
|
| [2] |
孟娜. 数字图像水印算法的研究与实现[D]. 西安: 西北大学, 2009. http://d.wanfangdata.com.cn/Thesis/Y1453288
|
| [3] |
黄继武, SHIYUN Q. 一种自适应图像水印算法[J]. 自动化学报, 1999, 25(4): 476-482. |
| [4] |
周素萍. 一种基于DWT的数字图像水印方法[J]. 科技咨询导报, 2007(12): 22-23. DOI:10.3969/j.issn.1674-098X.2007.12.016 |
| [5] |
胡承伟. 基于人眼视觉系统图像数字水印及研究[D]. 武汉: 武汉大学, 2005.
|
| [6] |
李建平. 抗打印扫描数字水印算法研究[D]. 西安: 西安电子科技大学, 2014. http://d.wanfangdata.com.cn/Thesis/D550820
|
| [7] |
单武扬. 基于支持向量机的半脆弱全息数字水印技术研究[D]. 株洲: 湖南工业大学, 2013. http://d.wanfangdata.com.cn/Thesis/D415505
|
| [8] |
MING SUN FU, A U, O C. Data hiding watermarking for halftone images. Image Processing[J]. IEEE Transactions on, 2002, 11(4): 477-484. |
| [9] |
姚海根. 数字加网技术[M]. 北京: 印刷工业出版社, 2000.
|
| [10] |
孙刘杰. 印刷图像处理[M]. 北京: 文化发展出版社, 2013.
|
| [11] |
万晓霞, 吴汉颖, 甘朝华. 基于多层次误差扩散加网的数字水印算法研究[J]. 武汉大学学报, 2007, 32(11): 1056-1059. |
| [12] |
路娜. 基于HVS模型的误差扩散算法的研究[D]. 开封: 河南大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10475-1013351716.htm
|
| [13] |
DAVID J LIEBERMAN, JAN P ALLEBACH. A dual interpretation for direct binary search and Its Implications for tone reproduction and texture quality[J]. Image processing, IEEEE transactions on, 2000, 9(11): 1950-1963. DOI:10.1109/83.877215 |
| [14] |
BAQAI F A, ALLEBACH J P. Halftoning via direct binary search using analytical and stochastic printer models[J]. Image Processing, IEEE Transactions on, 2003, 12(1): 1-15. DOI:10.1109/TIP.2002.806244 |
| [15] |
SANG H K, ALLEBACH J P. Impact of HVS models on model-based halftoning. Image Processing[J]. IEEE Transactions on, 2002, 11(3): 258-269. |
| [16] |
徐兴, 刘文涛. 基于半色调数字图像的水印技术研究[J]. 齐鲁工业大学学报, 2017, 31(4): 53-57. |
 2017, Vol. 31
2017, Vol. 31


