| 基于主成分分析和图论的低压配电网相户关系拓扑识别 |
随着社会经济和新能源技术的快速发展, 对电力系统末端的配电网标准化发展提出了更高要求。特别是分布式电源陆续接入配电网, 也加剧了网络的复杂性, 进一步导致电网运行状态会随新形势而开始频繁变化。配电网作为电力网中面向用户的重要一部分, 其运行状态的判断过程中会产生海量量测数据。因此如何利用现有量测数据及技术去进行配电网的拓扑识别变得极为重要[1]。
现有的拓扑分辨与识别技术在输电线路中应用较为成熟, 由于配网运行过程中网络协调, 负载平衡的处理, 导致网络可观性差难以实现实时运行拓扑观察。目前有基于设计实现拓扑结构辨识的装置, 利用信息注入装置实现微处理器的相别识别系统设计, 另外还有根据微处理器的相位识别系统和相别测量的信息注入的实物设计[2]。但在获得量测信息的前提下, 也不可避免导致了量测设备的增加, 势必引起设备成本问题的讨论。文献[3]针对于节能及线路精细化管理的要求, 提出了一种基于工频畸变脉冲电流技术的配电台区识别方法。缺点是对于电力线载波通信要求较高, 需要考虑成本的制约问题。
基于智能电表数据的拓扑识别的技术路线中, 主要依据电压数据的量测进行研究, 可以利用数字上电压幅值的大小来判断相应的位置信息。本质上是电压量测值进行相关分析来判断拓扑关系[4], 当采集数据量不足时, 单一量测的技术路线将无法适应应用场景。另一种技术路线[5], 利用配网负荷电压幅值大小因线路距离有区分的原因, 进行负荷间的排序, 原因在于二者在数值上表现的负相关性。文献[6]也提到通过对于更宽泛信息数据的分析思路, 结合配电变压器在后台设备易获取的量测信息记录, 进行相似度系数计算, 得到所在范围内“台变-用户”关系分析, 提供拓扑识别新思路。
本文提出了一种基于台区用户电表数据进行相位关系拓扑识别的方法。通过将电表数据进行预处理, 利用主成分分析(principal component analysis, PCA)算法得到约束矩阵, 结合图论(graph theory, GT)中有向图元素的定义原则, 判断并表示出低压配电网中分支与电表间的拓扑关系。利用某农村台区电表量测数据分析, 对数据进行去线损处理, 算法迭代出约束矩阵, 算例结果可以实现较为准确的相户关系拓扑识别。
1 低压配电网总体结构配电台区以配电变压器作为中心点进行区分, 辐射长度为固定值, 所覆盖区域内的用电用户, 即为台区内潜在用户。而变压器的相别则根据区域划定在辐射的扇形区域内, 实际中还会因为前期设计、地理位置、施工难度等客观因素, 使得区域划分及台变相别与理论规划存在差别[6]。
如图 1所示, 以配电网变压器作为辐射圆圈范围内的中心, 3个区域中的空心圆则表示低压供电网络末端安装智能电表的用户。而实际情况中, 辐射范围出现交叉的情况如图 2所示, 配电变压器的重合区域内用户的拓扑识别则成为工作重点, 本文假设台区内低压供电网络三相平衡, 且用户均为单相用户。
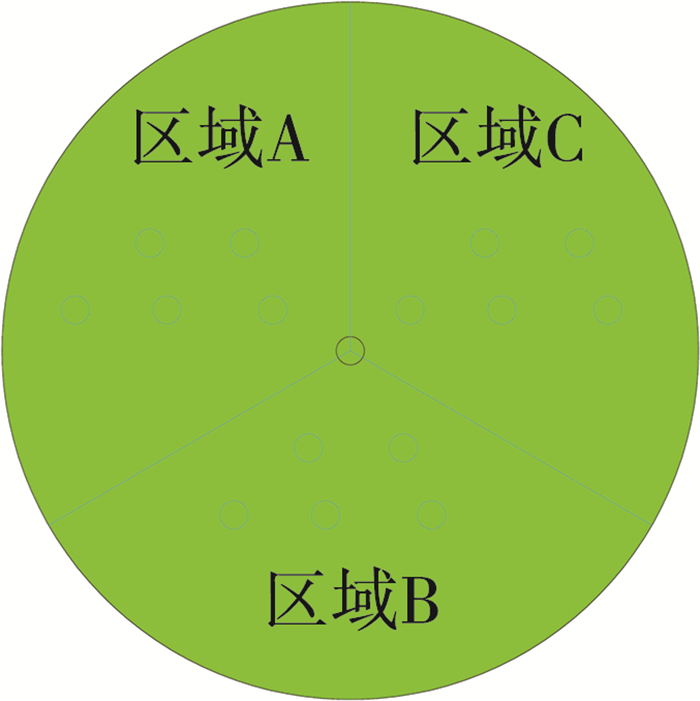 |
| 图 1 配电网台区变压器辐射图 |
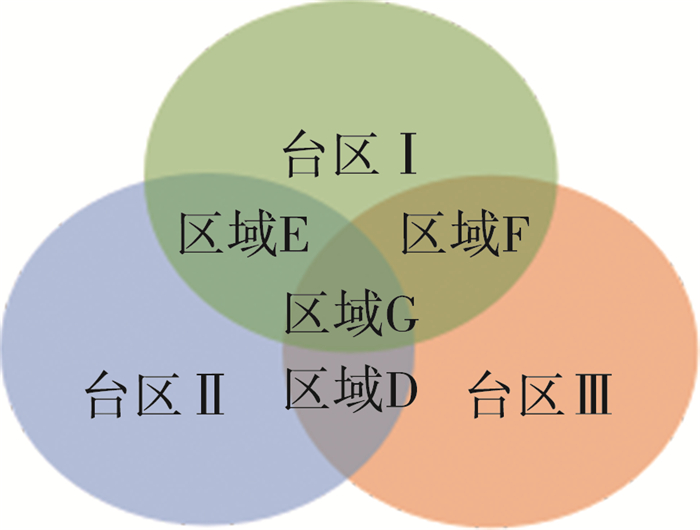 |
| 图 2 台区辐射交叉示意图 |
整体来说, 低压配电网经过对应电压等级的变配电设备, 将电能输送到电力用户侧, 它指的是对于10 kV/0.4 kV电压等级的配电变压器到用户电表的结构。其中, 10 kV电压等级的母线经过配电变压器转换后降为0.4 kV低压母线[7], 这一过程称一级配电; 在前一过程基础上, 经若干配电变压器后降为多条0.4 kV电压等级的分支馈线, 并通过电表箱进行分配, 此称为二级配电; 最后在前一步基础上将电能分配至不同的终端配电箱, 此过程称为终端配电。如图 3所示。
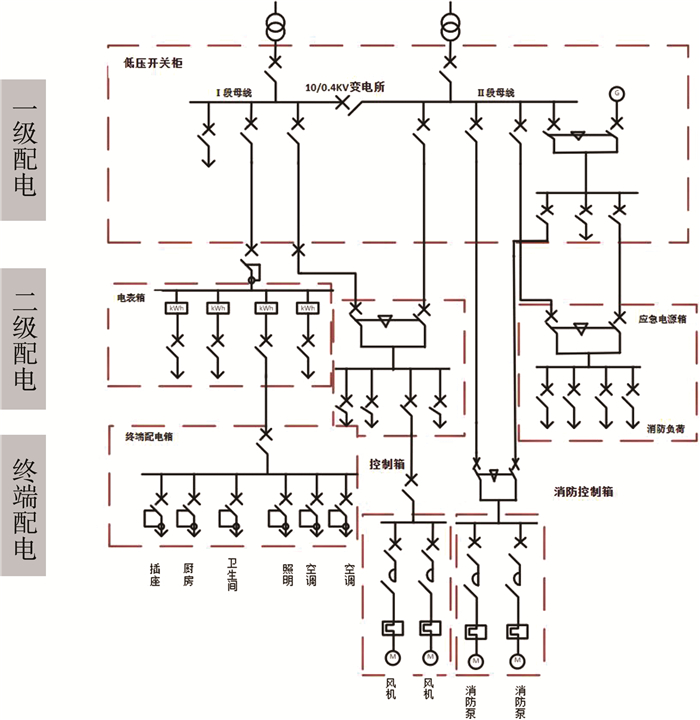 |
| 图 3 低压三级配电网络结构图 |
2 电表数据处理及拓扑识别应用 2.1 线路损耗误差估计
电表数据获取后, 不同用户的电能数据可能存在较大差异, 获取的数据需要处理后再应用。为消除干扰因素下电表数据受到的不合理影响, 需要进行电表数据标准化, 如式(1)所示:
| $ \varDelta W_{i}=\sum\limits_{j=1}^{n_{d}} w_{i j}^{d}-\sum\limits_{k=1}^{n_{i}} w_{i k}^{i} ; \forall i=1 \sim N, j=1 \sim n_{d}, $ | (1) |
式中, 等式左边代表第i个时间间隔内, 线路上所损失的电能值。右式中则代表第i个时间间隔内分支与用户间的电能差, 假设末端用户电压无剧烈变动, 则无论是电能损耗还是线损, 都可认为与电流成比例, 则线损可利用下式即可求得。
| $ \widehat{W} d_{i j}=W_{i j}^{d}-\frac{\left(W_{i j}^{d}\right)^{2}}{\sum\limits_{j=1}^{n_{d}}\left(W_{i j}^{d}\right)^{2}} \varDelta W_{i} ; \forall i=1 \sim N, j=1 \sim n_{d}, $ | (2) |
损耗误差计算的同时, 还应考虑到电表计时的误差。举例来说, 若电表的报告记录显示, 在某天1 h内记录用户所消耗电能为150 kW·h, 而实际上量测设备内部时钟与真实时钟相比有滞后, 假设滞后时间为1 min, 则记录报告中对应的时间段就会滞后显示1 min, 消耗电能值记录不变。因为电表实际运行中存在差异且各自之间并无关联, 可以认为电表记录中的此类误差实际为可忽略的随机误差。
2.2 基于PCA计算获得约束矩阵 2.2.1 主成分分析PCA主要用于获得多元数据的简约表示。本身作为一种多元的数据统计工具, 利用这一方法, 可以在正交变换的基础上, 求得线性无关变量。通过这一方法筛选出主成分后, 进行挖掘变量间潜在的线性关系。
定义Wx(j)是y个所获取数据电能表在第j个时间段内的量测数据值:
| $ W_{x}(j)=\left[W_{x 1}(j), W_{x 2}(j), \cdots, W_{x y}(j)\right], $ | (3) |
通常, 测量值会受到运行过程中随机噪声的污染, 进而出现样本中的误差。电能向量的另一种表示如下:
| $ W_{x}(j)=W_{t}(j)+e(j), $ | (4) |
上式中, Wt(j)代表j时刻电能的真实向量, 而e(j)是第j个时间间隔内的随机误差。假设误差通常是独立同分布的, 如下式(5)所示:
| $ e(j) \sim N\left(0, \sigma_{e}^{2} I\right), $ | (5) |
上式中, 描述的是j时刻的误差关于误差方差的正态分布, 最右边I代表单位矩阵, n代表电表数量。而线性关系模型数学表示如下:
| $ C W_{x}(j)=0, $ | (6) |
上式中, 约束矩阵C(k×y)维。对Wx(j), j =1, 2, 3, …,Y, 排列构成(y×Y)维电能W矩阵。通过式(6)可知, 降噪后的数据位于与约束矩阵子空间正交的子空间中。用PCA原理迭代出(k-p)维真实数据子空间和p维约束子空间。
2.2.2 奇异值分解在PCA算法中, 利用了协方差矩阵的特征向量Sw=WWT获得子空间, 同时使测量值和变量值的去噪估计值之间的平方差之和最小化[8]。选用奇异值分解(SVD)求取上述子空间:
| $ \operatorname{SVD}(W)=U_{1} S_{1} V^{\mathrm{T}}{ }_{1}+U_{2} S_{2} V^{\mathrm{T}}{ }_{2}, $ | (7) |
其中, S1和S2代表W的奇异值对角矩阵[9], 找到与该子空间正交的一组基向量后, 进行线性关系识别。又因选取的主成分与最小特征值相对应的特征向量U2有关, 在矩阵降维后, 约束模型由下式给出:
| $ U^{\mathrm{T}}{ }_{2} W=0, $ | (8) |
左式中U2T为约束矩阵, 且其不唯一。
| $ U^{\mathrm{T}}{ }_{2} W=\widehat{C} W=Q \widehat{C} W=0。$ | (9) |
由上式可知, Q是非奇异矩阵, 则估计约束矩阵实际上
回归模型可以通过将变量划分为因变量的集合Wd(nd=p)和自变量的集合Wi(ni=k-p)。估计约束矩阵的列对应于Wd和Wi, 有
| $ \widehat{c}_{d} w_{d}+\widehat{c}_{i} w_{i}=0, $ | (10) |
对于公式的前半部分, 矩阵满秩, 对公式变形处理, 得到估计回归矩阵:
| $ w_{d}=-\widehat{c}_{d}^{-1} \widehat{c}_{i} w_{i}=\widehat{R} w_{i} $ | (11) |
其中
| $ \widehat{R}=-\left(\widehat{c}_{d}\right)^{-1} \widehat{c}_{i}。$ | (12) |
连通图指的是至少有一条路径存在于每对节点之间的图。而树是没有回路的图, 而有向树的实质为没有回路连接的有向图。一个断开连接的图, 其组件为树, 称为树林。
图 4显示了一个具有三个树组件的有向森林。在有向图中, 父节点是具有指向另一个节点(也称子节点)的边的节点。如图 4所示, 节点b7, b8, b9是父节点3的子节点。
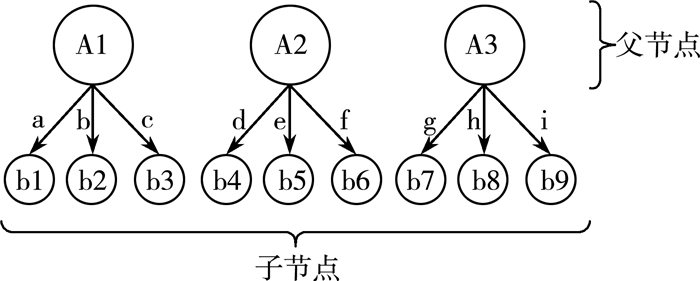 |
| 图 4 由三个树组件构成的森林 |
2.3.2 关联矩阵
图G=(NG, NE)的关联矩阵(A), 描述了节点上边的关联, 有向图的元素定义如下
| $ \boldsymbol{A}_{i j}=\left\{\begin{array}{c} +1, \text { 边 } j \text { 接入节点 } i \text { 的情况下 } \\ -1, \text { 边 } j \text { 离开节点 } i \text { 的情况下 }。\\ 0, \text { 边 } j \text { 不接触 } i \text { 的情况下 } \end{array}\right. $ |
对关联矩阵A进行分析, A的行代表节点的分布, 列则对应支路的分布。将A中行数据进行处理, 可变形得到:
| $ \boldsymbol{A}=\left[\begin{array}{l} \boldsymbol{A}_{e} \\ \boldsymbol{A}_{f} \end{array}\right], $ | (13) |
上式中, Ae与Af分别对应父结点和子节点所在的行。利用回归矩阵
| $ \boldsymbol{A}_{e}=\widehat{R}。$ | (14) |
因此, 可以从
本章利用电能守恒的原理, 将所要识别的电表上下级关系, 在充分考虑偏差影响的前提下, 进行电表数据的优化, 再进行迭代计算, 实现电表对应用户与相别间拓扑关系的辨识。
如图 5所示, 约束矩阵
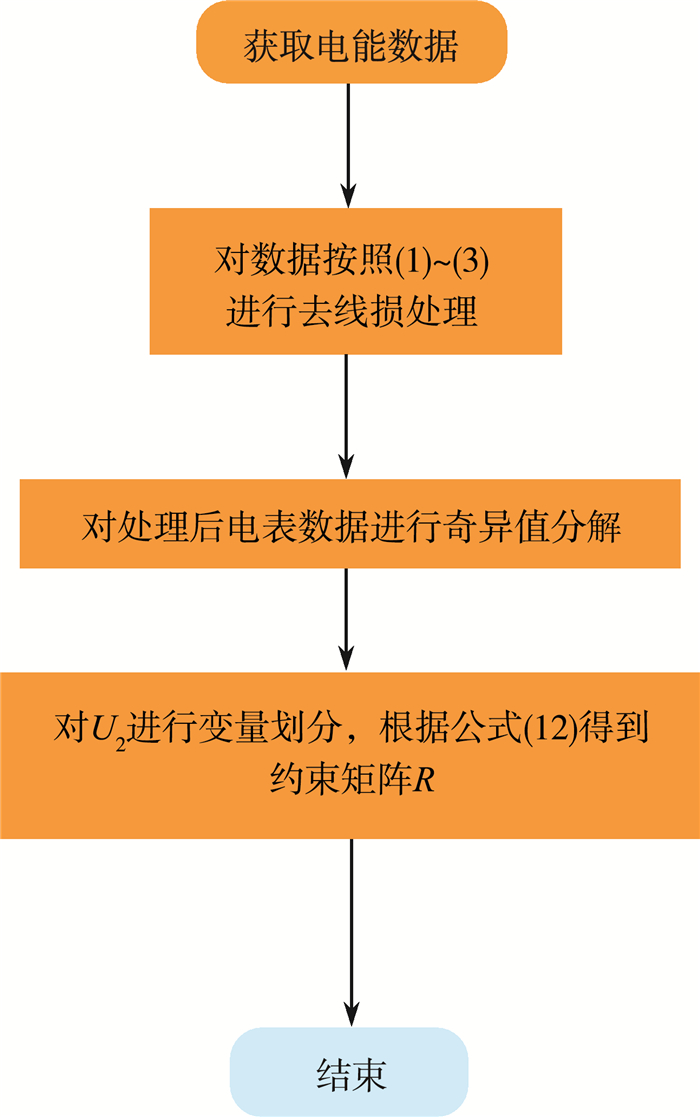 |
| 图 5 算法流程图 |
1) 首先对电能值数据处理, 去除支路所损耗电能值后, 再进行标准化处理。
2) 对处理后的电能数据, 按式(7)进行奇异值分解。
3) 按上文中图论的定义进行转换, 将每列数据中接近1的数据近似为1, 接近0的数据接近于0。
4) 根据式(12)求出关联矩阵, 并根据此推出上下级电表的隶属情况, 实现相位关系的拓扑识别。
4 算例分析及算法评价文章利用来自某农村台区10 d的电表数据, 如表 1所示, 包括3个分支电表和10个用户电表箱内量测数据, 利用上述方法进行拓扑识别的验证。
| 表 1 某台区8.11~8.20时间内测量电能数值 |
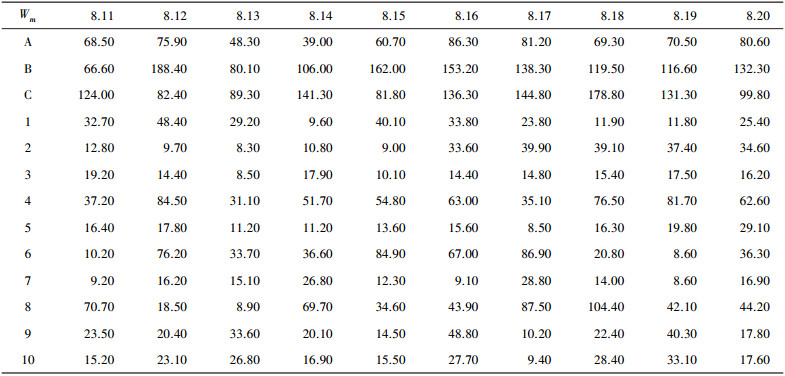 |
经过算法迭代计算, 首先将电能数据去线损, 降维后进行标准化处理, 再进行奇异值分解, 通过公式(12)得到表 2的约束矩阵, 根据有向图的元素定义, 对于接近1的数值, 判断用户与某一相别存在较强相关性, 对于趋近于0的数值, 可以判断相别与用户表箱无关。
| 表 2 算法计算后的约束矩阵 |
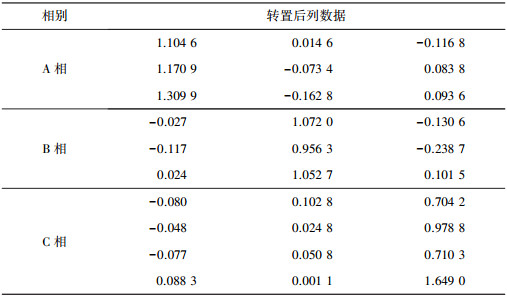 |
对上述结果进行转置, 可以更清晰的得出相别与用户之间存在的连接关系, 则相别与用户之间的拓扑关系, 如图 6所示。
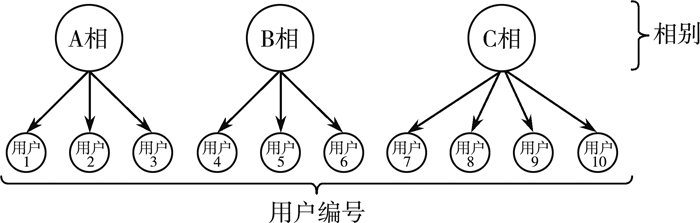 |
| 图 6 相别与用户间的拓扑关系表示 |
5 总结
文章提出了基于主成分分析和图论对低压配电网相户关系分析的拓扑识别方法。首先分析了低压配电网的总体结构, 指出台区交叉辐射所造成的相户拓扑关系的不正确识别问题, 利用量测设备记录的数据, 先对其中的电表数据进行去线损处理, 并分析了时钟不同步问题, 初步得到修正后的电表数据, 带入算法进行处理得出关联矩阵, 结合有向图的元素定义, 实现对用户相别关系的拓扑识别。针对农网建设中, 出现的低压配电网前期规划混乱, 导致对于线路末端拓扑识别不准确的情况, 提供了新的配网末端用户与相别关系的拓扑识别方法。
| [1] |
冯人海, 赵政, 谢生, 等. 基于主成分分析和凸优化的低压配电网拓扑识别方法[J]. 天津大学学报(自然科学与工程技术版), 2021, 54(7): 746-753. |
| [2] |
李彦兆, 赵庆生, 梁定康, 等. 基于量测信息的低压配电网阻抗拓扑模型构建[J]. 电网与清洁能源, 2021, 37(4): 15-22. DOI:10.3969/j.issn.1674-3814.2021.04.003 |
| [3] |
严永辉, 周瑞雪, 喻伟, 等. 基于载波和工频畸变技术的台区拓扑识别[J]. 自动化技术与应用, 2021, 40(10): 68-71. DOI:10.3969/j.issn.1003-7241.2021.10.016 |
| [4] |
闫卫国, 王高猛, 林济铿, 等. 基于AMI量测信息的低压配电网拓扑校验方法[J]. 中国电力, 2019, 52(2): 125-133. |
| [5] |
夏水斌, 余鹤, 董重重, 等. 基于集抄系统深化应用的低压台区电网拓扑重构方案[J]. 电测与仪表, 2017, 54(20): 110-115. DOI:10.3969/j.issn.1001-1390.2017.20.019 |
| [6] |
杨志淳, 沈煜, 杨帆, 等. 基于数据关联分析的低压配电网拓扑识别方法[J]. 电测与仪表, 2020, 57(18): 5-11. |
| [7] |
张波, 赵永红, 唐亮, 等. 基于AMI数据的城市低压配电网拓扑校验方法研究[J]. 电子测量技术, 2019, 42(6): 67-71. |
| [8] |
NARASIMHAN S, SHAH S L. Model identification and error covariance matrix estimation from noisy data using PCA[J]. Control Engineering Practice, 2008, 16(1): 146-155. |
| [9] |
NARASIMHAN S, BHATT N. Deconstructing principal component analysis using a data reconciliation perspective[J]. Computers & Chemical Engineering, 2015, 77: 74-84. |
| [10] |
PAPPU S J, BHATT N, PASUMARTHY R, et al. Identifying topology of low voltage distribution networks based on smart meter data[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 5113-5122. |
| [11] |
张丽强. 基于智能电表数据的供电网络拓扑识别方法研究[D]. 济南: 山东大学, 2020.
|
 2022, Vol. 36
2022, Vol. 36


