| 基于有限差分的燃油管道压力控制研究 |
高压油管是高压油路的组成部分,燃油进入和喷出高压油管是许多燃油发动机工作的基础,可用于工程机械液压油管、海底天燃气、石油、灌溉、钢厂、化工厂等介质的输送。高压油管连接着高压油泵和喷油机系统,通过压力差将油传送到发动机,如果压力控制不当,发动机进出油量不稳定,会出现发动机效率降低等一系列问题[1-4]。燃油进入和喷出的工作过程会导致高压油管内压力的变化,从而产生影响油管的安全和发动机的工作效率的可能。为此,如何对油管的压力进行较好的控制成为了我们需要解决的问题。
1 油管内压强分析 1.1 管内燃油压力与密度的关系 1.1.1 弹性模量与压力的关系依据经验公式判断数据拟合的压力-弹性模量函数,进而拟合出压力-密度函数。然后我们通过遍历循环方法,采用微元思想,设定循环进油量和循环喷油量,通过流体动态平衡分析法寻找稳定状态,不断迭代递推得到新的密度和压力。根据压差计算公式、管内平衡方程、油管流量公式和密度变化方程组,得到单向阀循环开启闭合的时间。最后改变压力稳定值后,利用周期特点和流体动态平衡分析,计算不同时长达到稳定时的开阀时间。
首先通过大量实验,我们得到了燃油密度和燃油体积弹性模量的经验公式
| $ \left\{ {\begin{array}{*{20}{c}} {\rho \left( {p, T} \right) = \left( {{a_0} + {a_2}T + {a_2}{T^2}} \right){e^{{a_c}{{\left( {p + {a_4} - {a_5}T} \right)}^{{a_6}}}}}}\\ {K\left( {p, T} \right) = 34.74{{\left( {p + {a_4} - {a_5}T} \right)}^{1 - {a_6}}}} \end{array}} \right. $ | (1) |
其中a均为常数,T为燃油温度。依据上式,我们大体判断压力与弹性模量的函数关系,先将2019年全国大学生数学建模竞赛中给出的弹性模量与压力的关系数据做出图像。
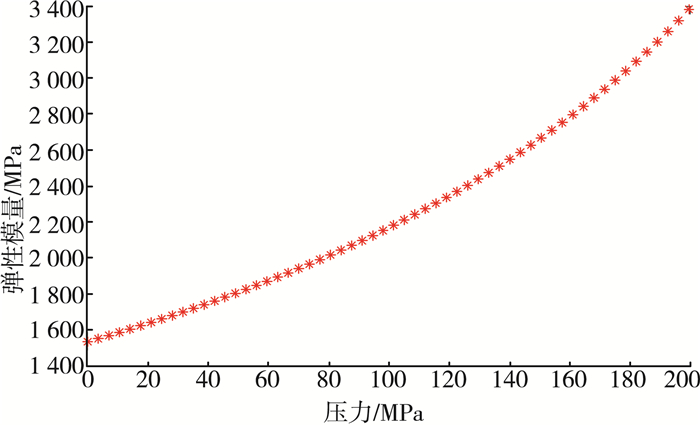 |
| 图 1 弹性模量与压力数据散点图 |
我们发现图像1近似为幂函数和指数函数关系图像,我们对函数两边取对数,幂函数取对数后呈非线性关系,而指数函数取对数后呈线性关系,以此区分。对于取对数后的数据,我们计算其和线性的相关系数R=corrcoef(A, B),得到结果为0.997 7,说明为指数函数关系。
基于微积分理论,且设弹性模量E在[p, Δp+p]内的改变量为
| $ \mathit{\Delta }E = E\left( {p + \mathit{\Delta }p} \right) - E\left( p \right) $ | (2) |
每一压力值下的模量改变量的速率为v,则有
| $ \mathit{\Delta }E = v \cdot E\left( p \right)\mathit{\Delta }p $ | (3) |
当压力改变量趋于0时,通过数据拟合,确定模量与压力关系的表达式为
| $ E = 645.377\;8{e^{0.006\;7p}} + 905.596\;3 $ | (4) |
燃油的压力变化量与密度变化量成正比,比例系数为
| $ \left\{ {\begin{array}{*{20}{c}} {p = {k_1}{\rho ^3} + {k_2}{\rho ^2} + {k_3}\rho + {k_4}}\\ {{k_1} = 4.307 \times {{10}^4}}\\ {{k_2} = - 1.000 \times {{10}^5}}\\ {{k_3} = 7.928 \times {{10}^4}}\\ {{k_4} = - 2.144 \times {{10}^4}} \end{array}} \right. $ | (5) |
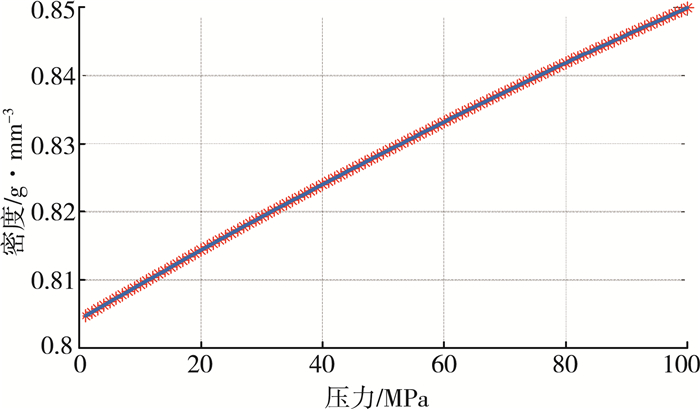 |
| 图 2 压力与密度数据拟合图 |
1.2 有条件简化情况下管内压强变化分析 1.2.1 考虑没有油泵没有针阀没有稳压阀
没有油泵、针阀及稳压阀的情况如图 3所示,由于进油时,油管内的压强会增大,喷油时会减小,为了保证整个进油出油过程管内压力稳定,我们需要达到油管内的燃油量趋于稳定,进行流体动态平衡分析。
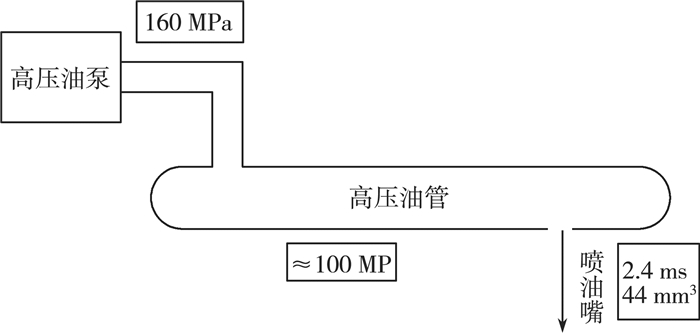 |
| 图 3 高压油管结构参数 |
喷油嘴的喷油规律为已知规律,即每100 ms进行一次喷油,且始终在初始的2.4 ms内喷出44 mm3,进油时通过高压油泵孔进油,受到油管内压强的影响。计算过程如图 4所示。
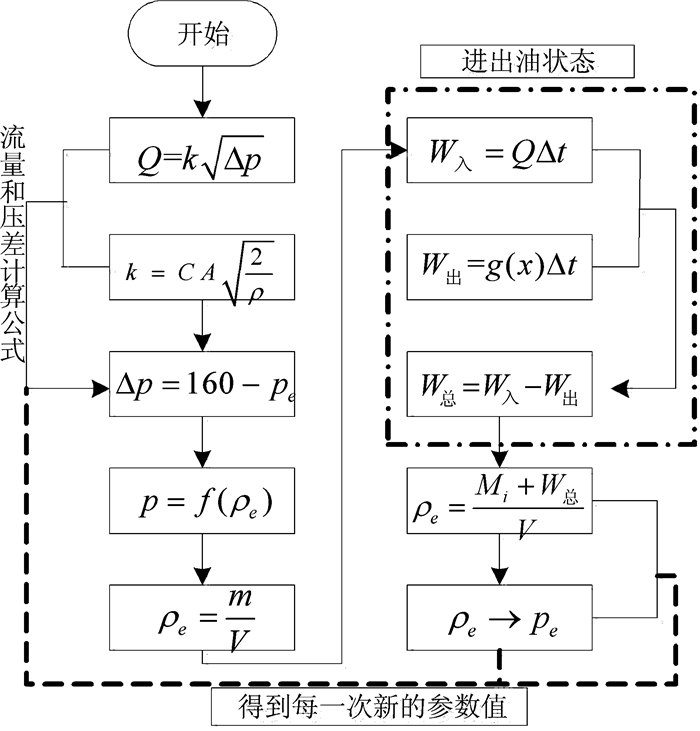 |
| 图 4 燃油系统的相关参数求解流程 |
1) 遍历循环
我们以1 000 ms为时间判定条件,遍历循环搜索每一次单向阀开启时间的进油量、压强,找出最优值,对于不同的开启时长,都进行一次平衡压力分析和step2、step3、step4。在0, 1区间内分为{0, 0.1…0.9, 1}10个时间曲线。由图 5可知喷油时间的最优值在0.2~0.3 ms之内。再次得到单向阀开启最优进油时间为0.27 ms。
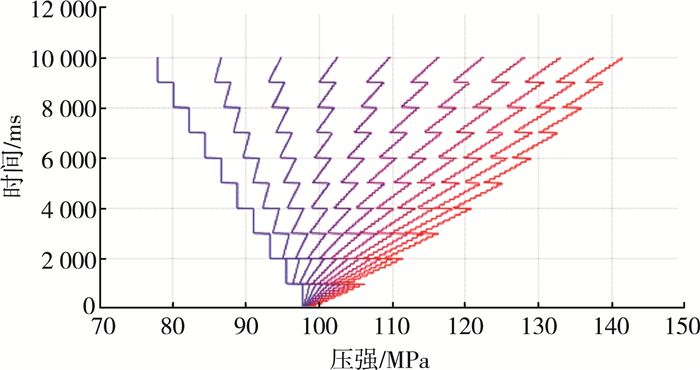 |
| 图 5 交替遍历中不同进油时间对压强关系 |
2) 进油状态
在一个100 ms的周期内,为保证高压油管的油量稳定。我们先对进油量作出分析,结合注释得到压差计算公式
| $ {W_入} = Q \cdot {\rho _1} \cdot \mathit{\Delta }t = f\left( x \right)CA\sqrt {\frac{{2\mathit{\Delta }p}}{{{\rho _1}}}} dt \cdot {\rho _1} $ | (6) |
其中Q中的变量Δp为压力的差值,f(x)为
| $ f\left( x \right)\left\{ {\begin{array}{*{20}{c}} {1, 开闸}\\ {0, 闭闸} \end{array}} \right. $ | (7) |
内部的压强变化我们根据得出的压强-密度函数求解。
3) 喷油状态
题中给出的喷油状态为周期性,在设定的100 ms内,喷油函数g(x)为
| $ g\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {100t, \;\;\;\;\;\;\;t \in \left[ {0, 0.2} \right]}\\ {20, \;\;\;\;\;\;t \in \left[ {0.2, 2.2} \right]}\\ {100 - 20t, \;\;\;\;\;\;t \in \left[ {2.2, 2.4} \right]}\\ {0\;\;\;\;\;\;t \in \left[ {2.4, 100} \right]} \end{array}} \right. $ | (8) |
我们计算一段时间内的出油量为
| $ {W_出} = \frac{{g\left( {{t_1}} \right) + g\left( {{t_2}} \right)}}{2}\left( {{t_2} - {t_1}} \right)\rho $ | (9) |
4) 整体流量
油管内燃油的变化量为进入及喷出燃油的代数和,进出的差值越小,高压油管越稳定。
| $ \left\{ {\begin{array}{*{20}{c}} {{W_总} = {W_入} - {W_出}}\\ {{W_总} \to p} \end{array}} \right. $ | (10) |
5) 流动后压力密度的分析
在计算时,每一次进油期间,因时间极短,进油量又少,我们采用微元思想,进行连续迭代计算。
| $ {\rho _新} = \left( {{W_总} + \rho V} \right)/V $ | (11) |
根据压力密度函数递推关系式,压力为
| $ \left\{ {\begin{array}{*{20}{c}} {{p_5} = {k_1}{\rho _5}^3 + {k_2}{\rho _5}^2 + {k_3}{\rho _5} + {k_4}}\\ {{k_1} = 4.307\;305\;844\;125\;906 \times {{10}^4}}\\ {{k_2} = - 1.000\;612\;513\;444\;515 \times {{10}^5}}\\ {{k_3}{\rm{ = }}7.928\;436\;637\;358\;622 \times {{10}^4}}\\ {{k_4}{\rm{ = }} - 2.144\;970\;334\;648\;115 \times {{10}^4}} \end{array}} \right. $ | (12) |
经过计算我们可以得出压力在98 MPa到101 MPa之间浮动,浮动较小,压力可以基本稳定在100 MPa左右。
1.2.2 考虑有油泵有一个针阀没有稳压阀1) 高压油泵的结构如图 6所示:
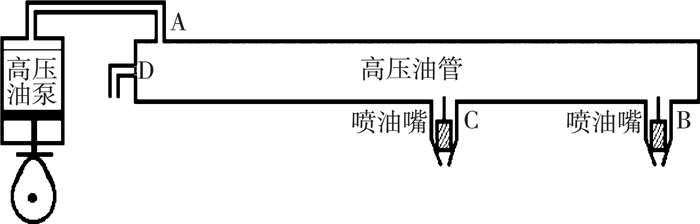 |
| 图 6 高压油管系统结构图 |
其通过凸轮转轴中心的旋转向高压油管内注油,高压油泵上方有一段残余容积,我们计算其高度为4.826 mm,油泵的最大体积为
| $ {V_1} = 114.516\;9{\rm{m}}{{\rm{m}}^3} $ |
分析凸轮边缘曲线,绘制出大体形状,并进行拟合函数得到极径与计较的关系如图 7所示。其中极径最小值为2.423 mm。
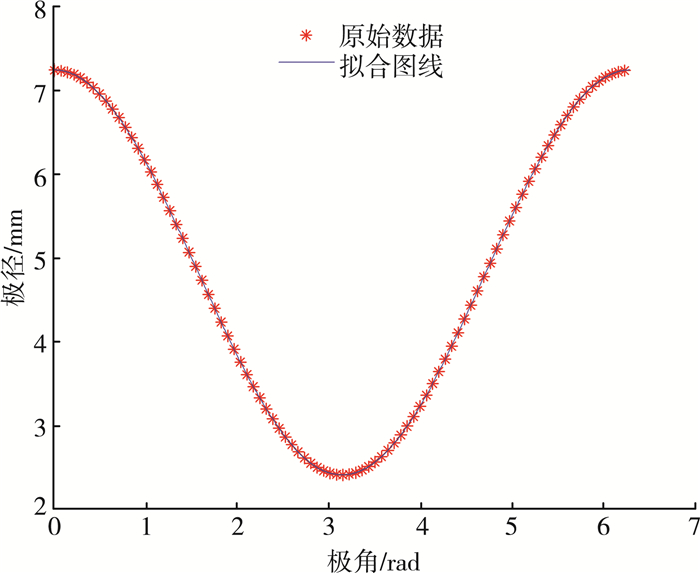 |
| 图 7 极径与极角的关系图 |
设定油泵的开始时间为供油的临界值,即油泵内的压力与油管内压力相等时开始[5]。我们采用有限差分法,认为每dt=0.01 ms内,油管内压力不变,当p>p′,我们根据柱塞抬升函数和流量公式列出油泵系统工作有限差分方程组。
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{W_i} = - C \cdot {A_1} \cdot \sqrt {\frac{{2\left( {{p_1} - {p_i}} \right)}}{{{p_1}}}} \cdot {\rho _i} \cdot dt\;\;\;, p > p'}\\ \begin{array}{l} {W_i} = {V_泵} \cdot \left( { - 6.602 \times {{10}^7}} \right) \cdot {p_{低压}}^2 + 5.234\;5 \times \\ {10^{ - 4}} \cdot {p_{低压}} + 0.804\;2 - {V_i}{\rho _i}\;\;\;, 3.13 < \alpha < 3.16 \end{array}\\ {{W_i} = 0\;\;\;\;\;, 其他} \end{array}} \right.\\ \end{array} $ | (13) |
其中W为油泵内燃油流量,即油管内燃油流入量,p低压为低压燃油的压力0.05 MPa。
2) 针阀喷油规律的分析
喷油过程由喷油最完成,其中喷油嘴针阀的结构如图 8所示:
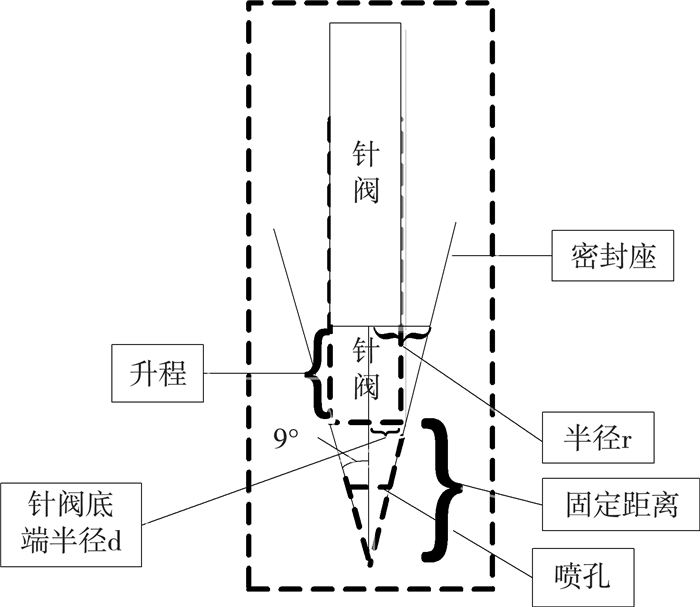 |
| 图 8 针阀运转结构 |
我们通过实验计算出了针阀的升程l与时间t的函数关系,一个周期为100 ms,t=0为一个周期的开始。
| $ l = \frac{{2.266}}{{1 + 4.591\;2 \cdot {e^{4.591\;2 - 18.635\;11}}}} $ | (14) |
在每一次喷油过程中,针阀上升或下降时,与密封座之间存在一定空隙,不同的空隙时喷油速率不同,且针阀的升程决定有效面积[6]。我们先寻找有效半径和升程之间的关系,对于整个高压油管,针阀升程造成的高低差对压力差的影响忽略,有效流通面积为
| $ \left\{ {\begin{array}{*{20}{c}} {S = \min \left\{ {\frac{{\rm{ \mathsf{ π} }}}{4}\left( {{r^2} - {d^2}} \right), {\rm{ \mathsf{ π} }} \times {{0.7}^2}} \right\}}\\ {r = \left( {d\mathit{cot}\frac{{\rm{ \mathsf{ π} }}}{{20}} + l} \right) \cdot \tan \frac{{\rm{ \mathsf{ π} }}}{{20}}} \end{array}} \right. $ | (15) |
其中l为针阀升程。
依次将上式代入,即可得到流通面积与时间的函数关系。根据有流通面积,我们可以将流通过程分为四个阶段。第一阶段是升程开始时,有效流通面积小于喷孔面积,计算时取有效流通面积。第二阶段为有效流通面积大于喷孔面积时,按喷孔面积计算,第三阶段针阀下降时,变化与上升时循环类似,针阀关闭时为第四阶段, 给出阀系统计算有效流通面积的可视化过程[7]。
[0, 100]开始,当t∈[0, 100]ms时
| $ \left\{ {\begin{array}{*{20}{c}} {{A_2} = {\rm{ \mathsf{ π} }}{r^2} - {\rm{ \mathsf{ π} }} \cdot {{125}^2}, t \in \left[ {0, 0.358\;5} \right)}\\ {{A_2} = {\rm{ \mathsf{ π} }} \cdot {{0.7}^2}, t = \left[ {0.358\;5, 2.091} \right)}\\ {{A_2} = {\rm{ \mathsf{ π} }} \cdot {r^2} - {\rm{ \mathsf{ π} }} \cdot {{1.25}^2}, t = \left[ {0.291, 2.46} \right)}\\ {{A_2} = 0, t = \left[ {2.45, 100} \right)} \end{array}} \right. $ | (16) |
3) 高压油管动态平衡分析
我们计算出凸轮转动的极角周期为6.283 1,我们规定,极角大于6.283 1后,则减去6.283 1,保证在2π周期内。根据实际,抬升高度为r(a)-min{r(a), [0, 2π]},并在每一时刻计算新的油泵体积,计算方程组
| $ \left\{ {\begin{array}{*{20}{c}} {{J_{i + 1}} = 2.153\cos \left( {2{\rm{ \mathsf{ π} }} - \omega {t_1} + {\omega _t}} \right) + 2.413}\\ {{V_{i + 1}} = {V_i} + {J_i}{\rm{ \mathsf{ π} }} \times {{2.5}^2} - {J_{i + 1}} \times {\rm{ \mathsf{ π} }} \times {{2.5}^2}} \end{array}} \right. $ | (17) |
根据压力密度递推式,计算高压油泵内新的密度和压强为
| $ \left\{ {\begin{array}{*{20}{c}} {{\rho _{i + 1}} = \frac{{{\rho _i} \cdot {v_i} + {w_i}}}{{{V_{i + 1}}}}}\\ {{p_{i + 1}} = p\left( {{\rho _{i + 1}}} \right)} \end{array}} \right. $ | (18) |
当高压油泵向高压油管内供油时,油管的针阀也会规律性开启,形成进油出油状态,我们对其动态平衡分析,压力仍取决于管内油量
| $ \left\{ {\begin{array}{*{20}{c}} {W'{\;_i} = - c \cdot {A_2} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{\rho '}_i} + {W_i}, \;\;p > p'}\\ {W'{\;_i} = - c \cdot {A_2} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{\rho '}_i}, \;\;\;\;其他} \end{array}} \right. $ | (19) |
计算高压油管内的新密度和压力为
| $ \left\{ {\begin{array}{*{20}{c}} {{{\rho '}_{i + 1}} = \frac{{{\rho _i} \cdot {V_{高压油管}} + {{W'}_i}}}{{{V_{高压油管}}}}}\\ {{{\rho '}_{i + 1}} = p\left( {{\rho _{i + 1}}} \right)} \end{array}} \right. $ | (20) |
通过改进的有限差分,我们综合高压油泵、高压油管、针阀的计算结果,求出凸轮的角速度为
| $ \omega = 0.294\;{\rm{rad/ms}} $ |
减压阀会在高压油管的压力达到阈值之后自动开启,使得高压油管内的燃油流入压强为0.5 MPa的低压油管,在不存在减压阀的情况下,高压油管的净流入量为高压油泵的流入量与针阀的流出量相减,即
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} W'{\;_i} = - C \cdot {A_2} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{\rho _1}}}} dt \cdot {{p'}_i} - \\ C \cdot {A_3}\sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{\rho _1}}}} dt \cdot p' + {W_i}, \;\;\;\;p > p' \end{array}\\ \begin{array}{l} W'{\;_i} = - C \cdot {A_2} \cdot \sqrt {\frac{{2({{p'}_1} - {p_气}}}{{{\rho _1}}}} dt \cdot {{p'}_i} - \\ C \cdot {A_3}\sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{p'}_i}, \;\;\;\;其他 \end{array} \end{array}} \right. $ | (21) |
而在增加了减压阀之后,我们应在判断p达到阈值之后令净流出量再次减去减压阀流出量:
| $ C \cdot {A_4} \cdot \sqrt {\frac{{2\left( {p' - 0.5} \right)}}{{{{p'}_i}}}} dt \cdot {{p'}_i} $ | (22) |
即p在达到阈值时,上式应变为
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} W'{\;_i} = - C \cdot {A_2} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{p'}_1} - \\ C \cdot {A_3} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{\rho '}_1} - m\left( p \right) \cdot C \cdot A \cdot \\ \sqrt {\frac{{2\left( {p' - 0.5} \right)}}{{{{\rho '}_1}}}} dt \cdot {{\rho '}_1} + {W_1}, \;\;\;\;p > p' \end{array}\\ \begin{array}{l} W'{\;_i} = - C \cdot {A_2} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{p'}_1} - \\ C \cdot {A_3} \cdot \sqrt {\frac{{2\left( {{{p'}_1} - {p_气}} \right)}}{{{{\rho '}_1}}}} dt \cdot {{\rho '}_1} - m\left( p \right) \cdot C \cdot A \cdot \\ \sqrt {\frac{{2\left( {p' - 0.5} \right)}}{{{{\rho '}_1}}}} dt \cdot {{\rho '}_1}, \;\;\;\;其他 \end{array} \end{array}} \right. $ | (23) |
在求解的过程中,我们先取时间间隔(50 ms),遍历找出第一次最优的角速度,取此最优角速度,遍历时间间隔,找到第一次最优的时间间隔,依次循环,直到一次的最优角速度等于上一次的最优角速度。增加减压阀后,我们使用遗传算法对不同的凸轮转轴角速度(αi-αi-)/t,减压阀阈值以及两个喷油嘴的喷油间隔进行求解,使得压力能稳定在100 MPa左右,对三个未知数进行编码,生成20行的父代矩阵,对父代矩阵进行交叉互换与变异,之后通过计算压强最大值与最小值的差选择出适应度最高的子代。进行50次进化,得到当前最优值并解码出三个未知数。
2 结论通过遗传算法,我们得到了使得高压油管内部压力稳定在100 MPa的凸轮转轴的最佳角速度为0.13 rad/ms,喷油策略为两个喷油管喷油间隔为47.1 ms,周期为100 ms,减压阀的阈值为100.1 MPa,在此情况下,高压油管内部最大的压力差,即pmax-pmin=2.711 7 MPa,在此情形下高压油管内压强随时间的变化如图 9所示。
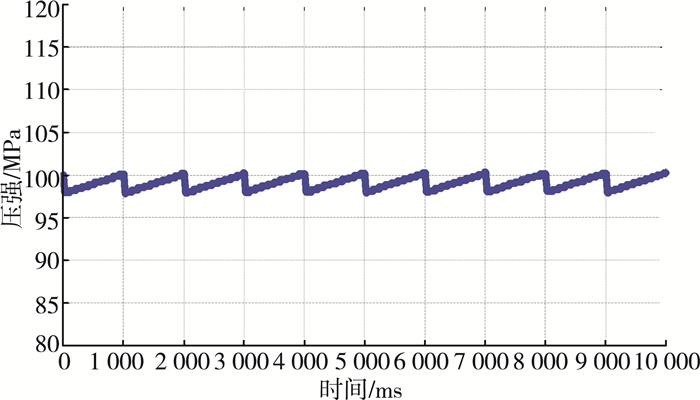 |
| 图 9 稳定的高压油管压力与时间关系 |
符号说明:
dt—时间元,ms
ρ—密度,mg/mm3
T—燃油温度,℃
K—经验公式中的弹性模量
E—弹性模量
v—模量改变率
p—高压油管内的压力,MPa
V—高压油管体积,mm3
W—油的流量,mm3
J—柱塞抬升高度,mm
α—极角
A1—油管截面积,mm2
A2—针阀有效流通面积,mm2
A3—双针阀有效流通面积,mm2
A4—减压阀管道截面积,mm2
| [1] |
张建明, 张卫刚, 王亚伟, 等. 柴油高压物理特性研究[J]. 高压物理学报, 2005, 19(1): 41-44. DOI:10.3969/j.issn.1000-5773.2005.01.008 |
| [2] |
HEESEON KIM, SOONHO SONG. Concept design of a novel reformer producing hydrogen for internal combustion engines using fuel decomposition method:Performance evaluation of coated monolith suitable for on-board applications[J]. International Journal of Hydrogen Energy, 2020, 45(16): 9353-9367. DOI:10.1016/j.ijhydene.2020.01.227 |
| [3] |
YONG QIAN, JIANPING WANG, ZILONG LI, et al. Improvement of combustion performance and emissions in a gasoline direct injection (GDI) engine by modulation of fuel volatility[J]. Fuel, 2020(268): 117369-117372. |
| [4] |
KAKOEE A., BAKHSHAN Y., BARBIER A., et al. Modeling combustion timing in an RCCI engine by means of a control oriented model[J]. Control Engineering Practice, 2020(97): 104321-104341. |
| [5] |
刘光新, 孙磊厚, 刘军华. 直喷汽油发动机高压油管耐压能力检测系统设计[J]. 机床与液压学报, 2018, 46(19): 84-88. |
| [6] |
白云.高压共轨燃油系统循环喷油量波动特性研究[D].哈尔滨: 哈尔滨工程大学, 2017.
|
| [7] |
钱李龙.喷油器入口压力波动及喷油控制研究[D].北京: 北京理工大学, 2015.
|
 2020, Vol. 34
2020, Vol. 34


