| 逻辑回归分类识别优化研究 |
逻辑回归分类是将标记好的数据通过机器学习总结归纳算法和分类模型或分类决策函数, 对数据进行输出预测[1]。通过输入离散或连续变量对输出有限离散值进行分类。本文分类识别由模型, 策略和算法三部分构成[2], 其中模型使用逻辑回归的方法解决分类问题的分类算法, 所输出的值在0到1之间。策略用代价函数来度量预测错误程度, 并将算法作为求解过程。
1 分类识别过程使用逻辑回归进行分类是基于现有的数据来建立分类边界线的回归公式, 以此进行分类[3]。逻辑回归使用优化算法寻找最佳拟合参数, 以及得到样本属于正类或者负类的可能性, 在多分类的系统中给出的是属于不同类别的可能性并进行分类。基本步骤如下:
步骤1:加载数据, 将采集到的训练集、测试集数据进行维度降低并转置, 转换为对应的结构化数值;
步骤2:创建数组, 设置权重维度为(dim, 1)的0向量, 偏差初始化为标量0;
步骤3:建立逻辑回归模型, 寻找h函数;构造J函数(损失函数);使J函数最小并求得回归参数θ;
步骤4:运行梯度下降算法, 优化循环的迭代次数, 并更新规则的学习率;
步骤5:根据训练的回归系数对数值进行简单的回归计算, 以确定它们类别。
2 建立逻辑回归模型 2.1 预估模型表示逻辑回归模型的假设:
| $ {h_\theta }(x) = g\left( {{\theta ^T}x} \right) $ | (1) |
其中x代表特征向量, g代表一个常用的逻辑函数(logistic function), S形函数(sigmoid function), 公式为:
| $ g(z) = \frac{1}{{1 + {e^{ - z}}}} $ | (2) |
其中z表示任何大小的标量或numpy数组。
Sigmoid函数在不同坐标尺下, 当x为0时, 函数值为0.5, 随着x增大, 函数的值无限接近于1;随着x的减小, 函数的值无限接近于0[4]。实际上, Sigmoid函数类似于一个阶跃函数。
逻辑回归可以看作是一种概率估计, 为实现逻辑回归分类器[5], 可以在每个特征上都乘以一个回归系数, 将所有的结果值相加, 并将这个总和代入Sigmoid函数, 进而得到一个在0~1之间的数值。所有大于0.5的数据被分入1类, 小于0.5的被归类为0类。
Sigmoid函数构造出的预估函数形式:
| $ {h_\theta }(x) = \frac{1}{{1 + {e^{ - \theta _x^T}}}} $ | (3) |
决策边界[6]由假设函数中参数决定将样本正确分类的一条边界, 在逻辑回归中预测:当hθ(x)大于等于0.5时, 预测y=1;当hθ(x)小于0.5时, 预测y=0。
根据绘制出的S形函数图像, 可以得出:
z=0时, g(z)=0.5
z>0时, g(z)>0.5
z < 0时, g(z) < 0.5
又z=θTx, 即:θTx大于等于0时, 预测y=1;θTx小于0时, 预测y=0。
不同的θ决定了不同的假设函数, 决策边界并不总是明确的, 特征空间中两类的过度是渐进的, 其中若决策平面是超平面那么分类是线性可分的。因此在这里认为θTx=0为决策边界, 当大于或小于0时, 根据逻辑回归模型预测不同的分类结果。
3 逻辑回归识别方法优化 3.1 代价函数表示一般把要最小化或最大化的函数称为目标函数或准则[7]。当最小化目标函数时, 称为代价函数、损失函数或误差函数[8]。一般分为0~1损失函数;平方损失函数;绝对值损失函数;对数损失函数;指数损失函数[9]。为了方便使用梯度下降法最小化代价函数, 在这里使用的代价函数是凸函数且没有局部最优值的对数损失函数。
在逻辑回归的代价函数为对数损失函数:
| $ j(\theta ) = \frac{1}{m}\sum\nolimits_{\rm{i} = 1}^{\rm{m}} {{\rm{Cost}}\left( {{h_\theta }\left( {{x^{(i)}}} \right),{y^{(i)}}} \right)} $ | (4) |
其中,
| $ \begin{array}{l} {\rm{Cost}}\left( {{h_\theta }\left( {{x^{(i)}},{y^{(i)}}} \right)} \right) = \\ \left\{ {\begin{array}{*{20}{l}} { - \log \left( {{h_\theta }(x)} \right)}& \ \ if \ \ {y = 1}\\ { - \log \left( {1 - {h_\theta }(x)} \right)}&\ \ if \ \ {y = 0} \end{array}} \right. \end{array} $ |
构建的函数Cost(hθ(x(i)), y(i)), 当y=1且hθ(x)也为1时, 误差为0;当y=1但hθ(x)不为1时, 误差随着hθ(x)变小而变大;当y=0且hθ(x)也为0时, 误差为0;当y=0但hθ(x)不为0时, 误差随着hθ(x)变大逐渐变大。简化的对数损失函数:
| $ \begin{array}{l} {\rm{Cost}}\left( {{h_\theta }\left( {{x^{(i)}},{y^{(i)}}} \right)} \right. = - y * \log \left( {{h_\theta }(x)} \right) - \\ (1 - y) * \log \left( {1 - {h_\theta }(x)} \right) \end{array} $ | (5) |
代入可得到代价函数:
| $ \begin{array}{l} J(\theta ) = - \frac{1}{m}\sum\nolimits_{i = 1}^m {\left[ {{y^{(i)}}\log \left( {{h_\theta }\left( {{x^{(i)}}} \right)} \right) + } \right.} \\ \left. {\left( {1 - {y^{(i)}}} \right)\log \left( 1 - {h_\theta }({x^{\left( i \right)}}) \right)} \right] \end{array} $ | (6) |
代入式(3)得:
| $ \begin{array}{*{20}{l}} {J(\theta ) = - \frac{1}{m}\sum\nolimits_{i = 1}^m {\left[ { - {y^{(i)}}\log \left( {1 + {e^{ - {\theta ^T}{x^{\left( i \right)}}}}} \right) + } \right.} }\\ {\left. {\left( {1 - {y^{(i)}}} \right)\log \left( {1 + {e^{ - {\theta ^T}{x^{\left( i \right)}}}}} \right)} \right]} \end{array} $ | (7) |
式(7)能很好地拟合训练集, 但是对未知数据, 测试集会被错误分类, 这就会出现过拟合。解决过拟合的方法有减少特征数量和正则化。由于特征越多训练会越好, 正则化可以在不减少特征的情况下解决过拟合。在代价函数后面添加惩罚项
| $ \begin{array}{l} J(\theta ) = - \frac{1}{m}\sum\nolimits_{i = 1}^m {\left[ { - {y^{(i)}}\log \left( {1 + {e^{ - {\theta ^T}{x^{(i)}}}}} \right) - } \right.} \\ \left. {\left( {1 - {y^{(i)}}} \right)\log \left( {1 + {e^{ - {\theta ^T}{x^{(i)}}}}} \right)} \right] + \frac{\lambda }{{2m}}\sum\nolimits_{j = 1}^n {\theta _j^2} \end{array} $ | (8) |
对式(8)函数求偏导:
| $ \begin{array}{l} \frac{\delta }{{\delta {\theta _j}}}J(\theta ) = \frac{\delta }{{\delta {\theta _j}}}\left[ { - \frac{1}{m}\sum\nolimits_{i = 1}^m {\left[ { - {y^{(i)}}\log (1 + } \right.} } \right.\\ \left. {\left. {{e^{ - {\theta ^T}{x^{(i)}}}}} \right) - \left( {1 - {y^{(i)}}} \right)\log \left( {1 + {e^{ - {\theta ^T}{x^{(i)}}}}} \right)} \right] + \\ \left. {\frac{\lambda }{{2m}}\sum\nolimits_{j = 1}^n {\theta _j^2} } \right] \end{array} $ | (9) |
通过化简式(9)得:
| $ \begin{array}{l} \frac{\delta }{{\delta {\theta _j}}}J(\theta ) = \frac{1}{m}\sum\nolimits_{i = 1}^m {\left[ {{h_\theta }\left( {{x^{(i)}}} \right) + {y^{(i)}}} \right]x_j^{(i)}} + \\ \frac{\lambda }{{4m}}\sum\nolimits_{j = 1}^n {{\theta _j}{{\bar \theta }_j}} \end{array} $ | (10) |
构造的代价函数是损失函数且为凸函数[10], 为了让代价函数的参数θ拟合出最佳参数, 在这里使用梯度下降法最小化损失函数来求函数的最小值[11]。梯度下降就是沿着梯度下降最快的方向求解极小值, 每次沿着偏导方向(下降速度最快方向)前进一小步, 直至N次迭代后到达最低点。为了求出最小的参数θ, 先随机初始化一个值, 接着迭代更新θ的值。用当前θ减去当前θ的梯度值与学习率α的乘积, 每次迭代都会得到一个新的θ, 经过一定次数的反复迭代后, 得到最终的θ值使得最小。
θ更新过程:
| $ {\theta _j}: = {\theta _j} - \alpha \frac{\delta }{{{\delta _{{\theta _j}}}}}J(\theta ) $ | (11) |
其中α为学习率。θ更新过程可以写成:
| $ {\theta _j}: = {\theta _j} - \alpha \frac{1}{m}\sum\nolimits_{i = 1}^m {\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^{(i)}}} \right)x_j^{(i)}} $ | (12) |
同样为了防止过拟合, 在式(12)添加惩罚项
| $ {\theta _j}: = {\theta _j} - \alpha \frac{1}{m}\sum\nolimits_{i = 1}^m {\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^{(i)}}} \right)x_j^{(i)}} + \frac{\lambda }{m}{\theta _j} $ | (13) |
合理选定步长的大小, 步长太大, 梯度可能会直接越过最优点, 飞到另外一侧;步长太小, 则需要迭代很多次才能到达最优点;把θ初始化在局部最优点, 说明θ的梯度为0, 更新的时候, θ不发生变化, 满足梯度的变化值小于指定阈值或者θ的变化值小于指定阈值迭代停止, 迭代结束后得到的θ值就是最终的结果。函数的导数随着接近极值点而逐渐减小, 因此只要让步长与函数的导数成正比, 就可以随着极值点的接近逐渐变小。图 1是所期望的梯度下降。
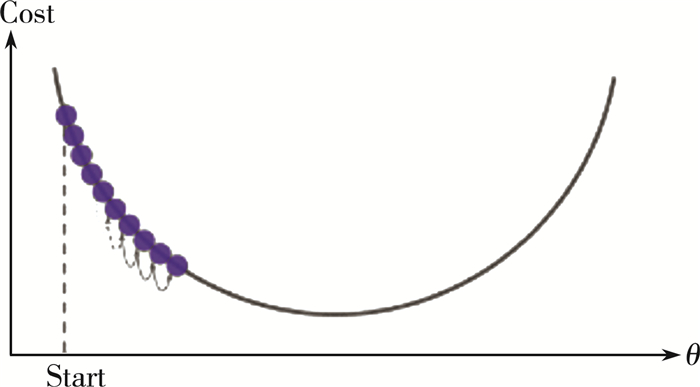 |
| 图 1 梯度下降 |
4 实验结果及分析
通过使用python语言建立正则化的逻辑回归模型, 利用逻辑回归模型和正则化后的逻辑回归模型分别进行图片预测, 得到以下实验结果。
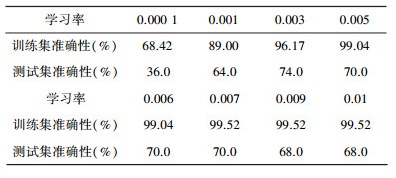
从表 1可以看出, 梯度下降算法的每次迭代都受学习率α的影响, 学习率决定了参数更新的速度。学习率α太小, 达到收敛所需的迭代次数将变大;相反学习率太大, 则每次迭代可能不会降低代价函数, 并且可能会超过局部最小值导致无法收敛。
| 表 1 逻辑回归学习率与准确性关系 |
 |
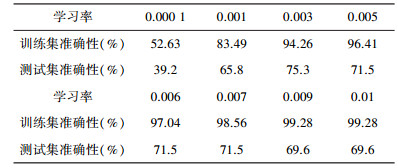
通过对比表 1和表 2, 可以看出正则化后的逻辑回归模型比逻辑回归模型在训练集中识别率有所降低但测试集中的识别准确率提高。梯度下降算法收敛所需要的迭代次数根据模型的不同而不同, 通过绘制算法不同学习率下代价函数的收敛曲线可直观了解。随着迭代次数的逐渐增加误差值逐渐减小, 曲线趋向于平滑, 如图 2所示。
| 表 2 正则化后逻辑回归学习率与准确性关系 |
 |
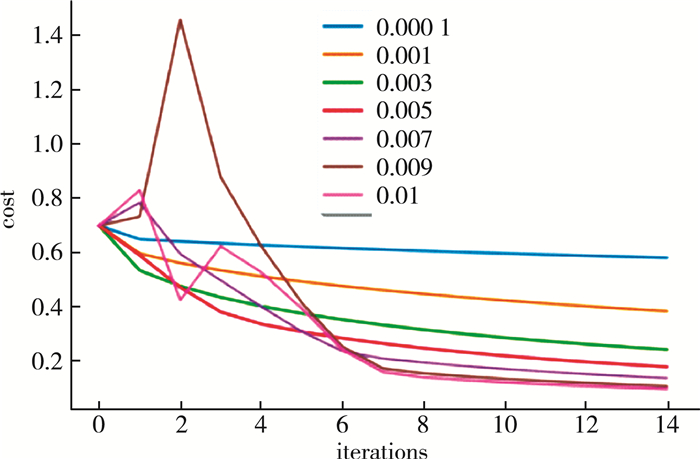 |
| 图 2 代价函数的收敛曲线 |
5 结语
本文通过实现逻辑回归成本函数的正则化, 使用梯度下降算法优化、更新权重和偏差, 优化循环的迭代次数使得学习率的规则更新, 大大确保了数据的正确性, 提高了待预测图片在测试集中出现概率的预测值。结果表明使用优化后的逻辑回归模型可以对权重和偏差优化、循环迭代次数可优化更新规则学习率, 使得训练集中识别率有所降低但测试集中的识别准确度提高。
| [1] |
EDITH LAW, BURR SETTLES, TOM MITCHELL. Machine learning and knowledge discovery in databases[M]. Springer Berlin Heidelberg, 2010.
|
| [2] |
王鑫, 李可, 徐明君, 等. 改进的基于深度学习的遥感图像分类算法[J]. 计算机应用, 2019, 39(02): 382-387. |
| [3] |
戴维. 逻辑回归解决文本分类问题[J]. 通讯世界, 2018(08): 266-267. DOI:10.3969/j.issn.1006-4222.2018.08.168 |
| [4] |
ALEXANDER Genkin, DAVID D LEWIS, DAVID MADIGAN. Large-scale bayesian logistic regression for text categorization[J]. Technometrics, 2007, 49(3): 291-304. DOI:10.1198/004017007000000245 |
| [5] |
胡智超.基于机器学习与启发式算法的物流调度研究[D].北京: 北京邮电大学, 2019. http://cdmd.cnki.com.cn/Article/CDMD-10013-1019042203.htm
|
| [6] |
黄费涛, 杨振国, 刘文印. 事件分类:使用DeepWalk学习的基线[J]. 工业控制计算机, 2019, 32(05): 122-124. DOI:10.3969/j.issn.1001-182X.2019.05.051 |
| [7] |
邓介一.大数据环境下的多分类逻辑回归算法研究与应用[D].武汉: 武汉工程大学, 2018.
|
| [8] |
马莉雅. 基于决策树、逻辑回归和改进神经网络的几种慢性病的危险因素分析研究(英文)[J]. 软件, 2014, 35(12): 58-65. DOI:10.3969/j.issn.1003-6970.2014.12.012 |
| [9] |
严晓明. 一种逻辑回归学习率自适应调整方法[J]. 福建师范大学学报(自然科学版), 2019, 35(03): 24-28. |
| [10] |
安波.基于逻辑回归模型的垃圾邮件过滤系统的研究[D].哈尔滨: 哈尔滨工程大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10217-2010075158.htm
|
| [11] |
马泽辉. 基于逻辑回归算法的Webshell检测方法研究[J]. 信息安全研究, 2019, 5(04): 298-302. |
 2019, Vol. 33
2019, Vol. 33


